使用python的加权Jaccard分析流程

1. ​​核心函数​​：

   • weighted_jaccard_similarity()：计算两个向量的加权Jaccard相似度

   • weighted_jaccard_matrix()：构建所有样本对的相似度矩阵

2. ​​数据处理​​：

   • 使用与原文相同的8×10矩阵

   • 添加行列标签（A-H对应样本，a-j对应特征）

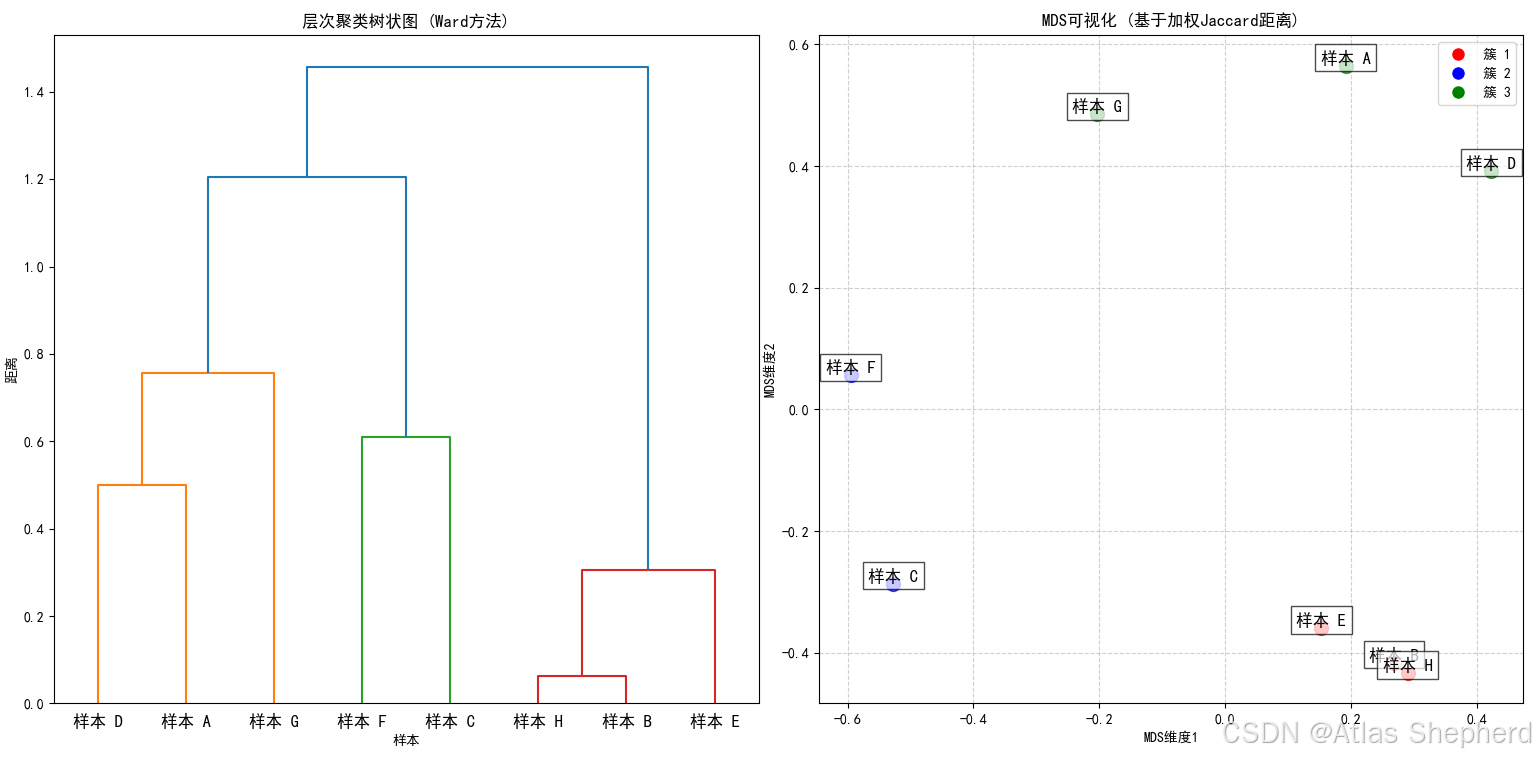
3. ​​层次聚类​​：

   • 将相似度矩阵转换为距离矩阵（1 - 相似度）

   • 使用Ward方法进行层次聚类

   • 可视化树状图并标注样本名称

4. ​​聚类分析​​：

   • 将样本划分为3个簇

   • 输出每个样本的簇分配

5. ​​MDS可视化​​：

   • 基于距离矩阵进行多维尺度分析

   • 在2D空间展示样本分布

   • 使用不同颜色标记不同簇的样本

   • 添加样本标签和图例

   import numpy as np
   import pandas as pd
   import matplotlib.pyplot as plt
   from scipy.spatial.distance import squareform
   from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
   from sklearn.manifold import MDS
   from itertools import combinations
   import matplotlib as mpl
   import matplotlib.font_manager as fm

   设置中文字体支持

   plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
   plt.rcParams['axes.unicode_minus'] = False # 正确显示负号

   def weighted_jaccard_similarity(vec1, vec2):
   """
   计算两个向量之间的加权Jaccard相似度

    参数:
    vec1, vec2 -- 输入向量(必须是非负数值)
   
    返回:
    相似度值 [0,1]
    """
    # 确保向量为非负
    if np.any(vec1 < 0) or np.any(vec2 < 0):
        raise ValueError("输入向量必须包含非负值")
   
    # 计算分子(最小值之和)和分母(最大值之和)
    numerator = np.sum(np.minimum(vec1, vec2))
    denominator = np.sum(np.maximum(vec1, vec2))
   
    # 处理分母为零的情况
    if denominator == 0:
        return 0.0
    return numerator / denominator

   def weighted_jaccard_matrix(data):
   """
   计算所有样本对之间的加权Jaccard相似度矩阵

    参数:
    data -- 二维数组或DataFrame (样本×特征)
   
    返回:
    相似度矩阵
    """
    n = data.shape[0]
    sim_matrix = np.zeros((n, n))
   
    # 计算所有样本对的相似度
    for i, j in combinations(range(n), 2):
        sim = weighted_jaccard_similarity(data[i], data[j])
        sim_matrix[i, j] = sim
        sim_matrix[j, i] = sim
   
    # 对角线设为1 (每个样本与自身完全相似)
    np.fill_diagonal(sim_matrix, 1)
    return sim_matrix

   创建示例数据 (与原文相同的矩阵)

   data = np.array([
   [2, 5, 2, 1, 0, 0, 0, 0, 1, 0],
   [0, 0, 0, 1, 3, 5, 6, 0, 0, 1],
   [0, 0, 0, 2, 0, 0, 1, 2, 7, 2],
   [4, 6, 2, 5, 1, 0, 0, 1, 0, 0],
   [0, 1, 0, 0, 3, 5, 4, 0, 0, 1],
   [0, 0, 1, 0, 0, 2, 0, 3, 5, 7],
   [3, 1, 4, 0, 1, 0, 0, 0, 0, 2],
   [0, 0, 0, 1, 3, 4, 6, 0, 0, 1]
   ])

   添加行列名称

   row_names = [f"样本 {chr(65 + i)}" for i in range(8)]
   col_names = [f"特征 {chr(97 + i)}" for i in range(10)]

   1. 计算加权Jaccard相似度矩阵

   jac_sim = weighted_jaccard_matrix(data)
   print("加权Jaccard相似度矩阵:")
   print(pd.DataFrame(jac_sim, index=row_names, columns=row_names).round(3))

   2. 转换为距离矩阵并进行层次聚类

   jac_dist = 1 - jac_sim
   condensed_dist = squareform(jac_dist) # 转换为压缩距离矩阵

   使用Ward方法进行层次聚类

   linked = linkage(condensed_dist, method='ward')

   划分聚类 (3个簇)

   clusters = fcluster(linked, t=3, criterion='maxclust')
   cluster_map = {name: cluster for name, cluster in zip(row_names, clusters)}
   print("\n样本聚类分配:")
   for sample, cluster in cluster_map.items():
   print(f"{sample}: 簇 {cluster}")

   3. MDS可视化

   mds = MDS(n_components=2, dissimilarity='precomputed', random_state=42)
   mds_results = mds.fit_transform(jac_dist)

   4. 在一个窗口中显示所有可视化

   plt.figure(figsize=(18, 8))

   左侧：树状图

   plt.subplot(1, 2, 1)
   dendrogram(linked,
   orientation='top',
   labels=row_names,
   distance_sort='descending',
   show_leaf_counts=True,
   color_threshold=0.7 * max(linked[:, 2]))
   plt.title('层次聚类树状图 (Ward方法)')
   plt.ylabel('距离')
   plt.xlabel('样本')

   右侧：MDS可视化

   plt.subplot(1, 2, 2)
   colors = ['red', 'blue', 'green'] # 对应3个簇

   for i, (x, y) in enumerate(mds_results):
   cluster_id = clusters[i] - 1 # 簇ID从0开始
   plt.scatter(x, y, c=colors[cluster_id], s=100, alpha=0.7)
   plt.text(x, y, row_names[i], fontsize=12,
   ha='center', va='bottom',
   bbox=dict(facecolor='white', alpha=0.7))

   plt.title('MDS可视化 (基于加权Jaccard距离)')
   plt.xlabel('MDS维度1')
   plt.ylabel('MDS维度2')
   plt.grid(True, linestyle='--', alpha=0.6)

   添加图例

   from matplotlib.lines import Line2D

   legend_elements = [Line2D([0], [0], marker='o', color='w', label=f'簇 {i + 1}',
   markerfacecolor=color, markersize=10)
   for i, color in enumerate(colors)]
   plt.legend(handles=legend_elements, loc='best')

   plt.tight_layout()
   plt.show()