量子计算学习笔记
量子计算核心原理学习笔记
量子力学基础
量子计算的理论基础源于量子力学的反直觉特性。双缝干涉实验是理解其核心的起点:单个粒子在未被观测时表现出波动性,能够像波一样同时穿过两条缝隙并与自身发生干涉。然而1,一旦引入测量设备试图确定其路径,干涉现象便会消失,粒子展现出确定的粒子性。这揭示了两个基本原则:
- 量子叠加 (Superposition) :在测量之前,一个量子系统可以存在于其所有可能状态的叠加态中。
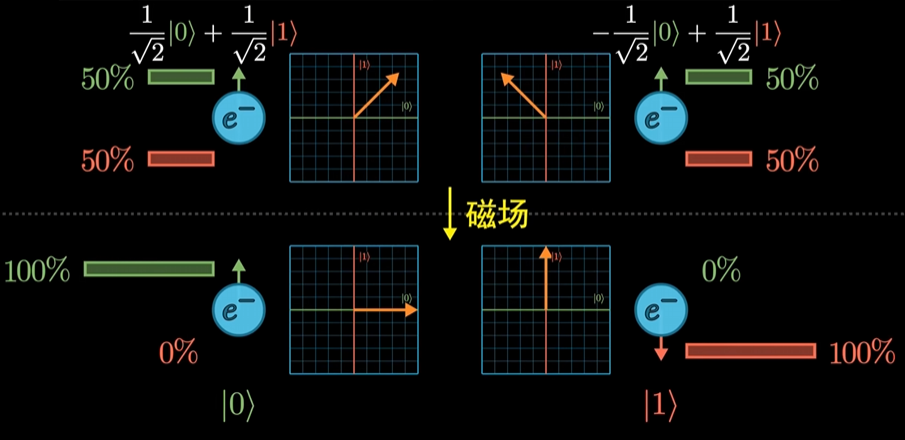
- 坍缩:测量行为会不可逆地改变系统状态,迫使叠加态"坍缩"到一个确定的经典状态。
量子比特 (Qubit)
经典计算机的基本单位是比特(bit),其值严格为0或1。量子计算的基本单位是量子比特(qubit),它利用叠加原理,可以同时是0和1的组合。一个量子比特的状态可以用一个二维复向量空间中的单位向量来表示,通常写作狄拉克符号(Bra-ket notation): ∣ ψ ⟩ = a ∣ 0 ⟩ + b ∣ 1 ⟩ |\psi\rangle = a|0\rangle + b|1\rangle ∣ψ⟩=a∣0⟩+b∣1⟩
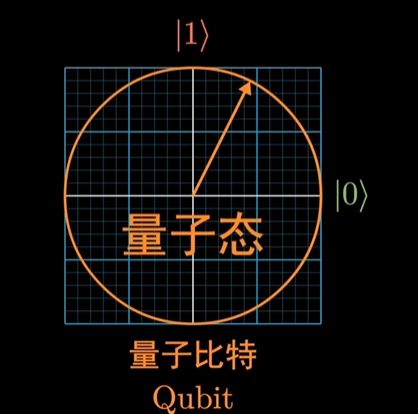
其中,|0⟩ 和 |1⟩ 是计算基矢,分别对应经典比特的0和1。系数 a a a 和 b b b 是复数,称为概率幅。它们必须满足归一化条件: ∣ a ∣ 2 + ∣ b ∣ 2 = 1 |a|^2 + |b|^2 = 1 ∣a∣2+∣b∣2=1。 ∣ a ∣ 2 |a|^2 ∣a∣2 和 ∣ b ∣ 2 |b|^2 ∣b∣2 分别是当测量该量子比特时,其状态坍缩到|0⟩或|1⟩的概率。一个量子比特因其概率幅可以取连续值,所能携带的信息远超一个经典比特。
并行性与纠缠
量子计算的潜力主要来自两个方面:
- 量子并行性 :一个由 n 个量子比特组成的系统,其状态空间维度为 2 n 2^n 2n。这意味着一个n-qubit的寄存器可以同时处于所有 2 n 2^n 2n 个可能状态的叠加之中。对这个寄存器进行一次量子门操作,其效果等同于对 2 n 2^n 2n 个数值同时进行运算,实现了指数级的数据处理能力。

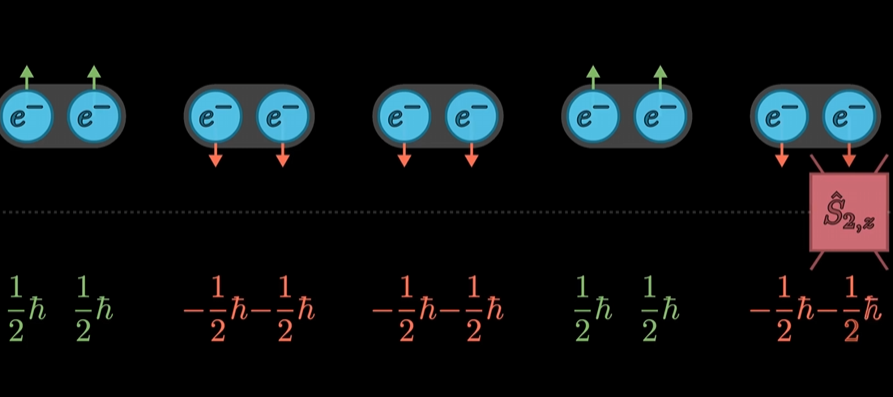
- 量子纠缠 (Entanglement) :多个量子比特可以进入一种非局域的关联状态,即使它们在空间上分离,其状态也不再独立。一个典型的两比特纠缠态是: 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) 2 1(∣00⟩+∣11⟩)。对这个系统进行测量,结果只可能是
00或11,且概率各为50%。一旦测量第一个比特得到0,第二个比特的状态会瞬间确定为0,反之亦然。这种强关联性是许多复杂量子算法得以实现的关键。
尽管量子计算机确实在 2 n 2^n 2n 的叠加态上同时演化,但在测量时,系统会根据概率波函数坍缩到一个随机的本征态。因此,我们无法一次性读出所有计算结果。
量子算法的精髓在于巧妙地利用量子干涉原理:通过精确设计的量子门序列,让通往错误答案的计算路径因相位不同而相互抵消,而通往正确答案的路径则相互增强。 最终,使得测量时系统以极高的概率坍缩到正确的解上。
量子门与量子算法
对量子比特的操作是通过量子门实现的,它们是量子线路的基本组成部分,本质上是对量子态向量进行幺正变换,保证了操作的可逆性。
- Hadamard门 (H门) :用于创建叠加态。它能将基态转换为均匀叠加态:
H ∣ 0 ⟩ = ∣ 0 ⟩ + ∣ 1 ⟩ 2 H|0\rangle = \frac{|0\rangle + |1\rangle}{\sqrt{2}} H∣0⟩=2 ∣0⟩+∣1⟩
H ∣ 1 ⟩ = ∣ 0 ⟩ − ∣ 1 ⟩ 2 H|1\rangle = \frac{|0\rangle - |1\rangle}{\sqrt{2}} H∣1⟩=2 ∣0⟩−∣1⟩ - CNOT门 (受控非门) :用于创造纠缠。它有两个输入:一个控制比特和一个目标比特。只有当控制比特为
|1⟩时,目标比特的状态才会翻转。
量子门是构建强大量子算法的工具,其中经典的量子算法包括:
-
Deutsch-Jozsa算法:证明了量子计算机解决特定问题,判断函数是常数还是平衡的效率高于经典计算机,经典需要多次查询,而量子仅需一次。
-
Grover搜索算法 :用于无序数据库搜索。经典算法的复杂度为 O ( N ) O(N) O(N),而Grover算法利用振幅增益技术,复杂度仅为 O ( N ) O(\sqrt{N}) O(N ),实现了二次方加速。
-
Shor算法:用于大整数质因数分解。该算法将分解问题巧妙地转化为寻找一个周期函数的周期问题,并利用量子傅里叶变换高效求解,实现了对经典算法的指数级加速。这使得Shor算法对基于RSA加密的现代密码学构成了根本性威胁。
量子退相干效应
量子态极其脆弱,与环境的任何微小相互作用都会破坏其量子特性,导致信息丢失,使量子计算的行为退化为经典概率计算。所有量子运算都必须在远小于退相干时间的尺度内完成。因此,延长量子比特的相干时间、提高量子门的保真度、以及发展量子纠错技术,是当前量子计算硬件发展的核心研究方向。
学习视频地址如下:https://www.bilibili.com/video/BV1ZYaYzDEuo/?vd_source=3e27296b0d1a61a78610cefe50bab13d