如何用Python找到股票的支撑位和压力位？——斐波那契

炒股的时候，大家经常听到一句话：支撑位和压力位很关键。如果把股价的运行比作人在大楼里走动，支撑位就像地板，会把人托住；压力位就是天花板，会挡住人往上冲。

那问题来了：这些地板和天花板到底在哪？ 🤔 今天花姐就带大家看看一个经典的工具------斐波那契。

开始前的准备

我这里用的行情数据源是 xtquant + miniQMT 。后续示例里会用到一些常见的 Python 库：pandas, numpy, matplotlib，进阶部分还会涉及 scipy, sklearn。在实际运行代码之前，记得先把环境配置好：

bash 复制代码

pip install pandas numpy matplotlib scipy scikit-learn xtquant

这样就能避免因为依赖缺失导致的报错啦。

以下是一个基于xtquant + miniQMT获取股票行情的方法，后面的行情Dataframe数据都会通过这个方法来获取：

python 复制代码

def get_hq(code,start_date='19900101',period='1d',dividend_type='front_ratio',count=-1):
    '''
    基于xtquant下载某个股票的历史行情
    盘中运行最后一个K里存了最新的行情
    period 1d 1w 1mon
    dividend_type - 除权方式，用于K线数据复权计算，对tick等其他周期数据无效
    none 不复权
    front 前复权
    back 后复权
    front_ratio 等比前复权
    back_ratio 等比后复权
    '''
    xtdata.enable_hello = False
    xtdata.download_history_data(stock_code=code, period='1d',incrementally=True)
    history_data = xtdata.get_market_data_ex(['open','high','low','close','volume','amount','preClose','suspendFlag'],[code],period=period,start_time=start_date,count=count,dividend_type=dividend_type)
    print(history_data)
    df = history_data[code]

    df.index = pd.to_datetime(df.index.astype(str), format='%Y%m%d')
    df['date'] = df.index
    return df

一、斐波那契的由来

斐波那契（Fibonacci，本名列昂纳多·比萨）是13世纪意大利的一位数学家。

他提出了一个很有意思的问题：

如果一对兔子每个月都会生一对新的兔子，而新兔子在第二个月开始繁殖，那么经过若干个月，会有多少对兔子？ 🐇🐇

为了回答这个问题，他推导出了一个数列：

1, 1, 2, 3, 5, 8, 13, 21...

这个就是著名的 斐波那契数列。

数列里有一个很神奇的规律：

每一项都是前两项的和；
随着数列往后延伸，相邻两项的比例会越来越接近 0.618。

而 0.618 在自然界里无处不在：

向日葵花盘的螺旋排列 🌻
贝壳的螺旋曲线 🐚
人体的黄金比例

这种普遍存在的规律被称为"黄金分割"，后来被引入金融市场。大家发现股价的波动也常常在这些比例附近表现出支撑或压力，于是便发展出了 斐波那契回撤 这一技术工具。

二、斐波那契回撤的原理

斐波那契数列大家或多或少都听过：1, 1, 2, 3, 5, 8, 13... 这个数列的相邻数字比例，会逐渐趋近于 0.618，也就是著名的"黄金分割"。

在金融市场中，常用的斐波那契比例有：

0.236
0.382
0.5
0.618
0.786

当股价在某段时间里走出一个高点 H 和低点 L，我们就可以用这些比例来推算潜在的支撑和压力区域。

市场里很多投资者会关注这些点位，自然就容易形成"共识心理"，价格也更容易在这些区域发生反应。

三、公式推导与指标说明 ✨

区间定义

区间最高价： <math xmlns="http://www.w3.org/1998/Math/MathML"> H = max ⁡ ( H i g h ) H = \max(High) </math>H=max(High)
区间最低价： <math xmlns="http://www.w3.org/1998/Math/MathML"> L = min ⁡ ( L o w ) L = \min(Low) </math>L=min(Low)
区间差值： <math xmlns="http://www.w3.org/1998/Math/MathML"> D = H − L D = H - L </math>D=H−L

回撤位公式

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> R ( p ) = H − D × p R(p) = H - D \times p </math>R(p)=H−D×p

其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> p p </math>p 就是斐波那契比例（0.236, 0.382, 0.5, 0.618, 0.786）。

应用解释

如果市场是上涨趋势 ：这些回撤价位就是潜在支撑位。
如果市场是下跌趋势 ：这些回撤价位就是潜在压力位。

直观示例 假设一只股票从 10 涨到 20 ，差值 <math xmlns="http://www.w3.org/1998/Math/MathML"> D = 20 − 10 = 10 D = 20 - 10 = 10 </math>D=20−10=10。

0.618回撤位：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> R ( 0.618 ) = 20 − 10 × 0.618 = 13.82 R(0.618) = 20 - 10 \times 0.618 = 13.82 </math>R(0.618)=20−10×0.618=13.82

也就是说，13.82 附近可能就是股价的支撑位。

四、Python实战代码

这段代码的功能是：先从指定股票获取历史行情数据，然后根据最近一段时间的收盘价找到最高点和最低点，计算出斐波那契回撤线，用来标记价格可能的支撑和阻力位，并将股价走势、回撤线以及最高点和最低点可视化展示，帮助投资者直观判断股票的趋势和关键价格区间，同时将0.618的线重点画成金色。

python 复制代码

from xtquant import xtdata
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def get_hq(code,start_date='19900101',period='1d',dividend_type='front_ratio',count=-1):
    '''
    基于xtquant下载某个股票的历史行情
    盘中运行最后一个K里存了最新的行情
    period 1d 1w 1mon
    dividend_type - 除权方式，用于K线数据复权计算，对tick等其他周期数据无效
    none 不复权
    front 前复权
    back 后复权
    front_ratio 等比前复权
    back_ratio 等比后复权
    '''
    xtdata.enable_hello = False
    xtdata.download_history_data(stock_code=code, period='1d',incrementally=True)
    history_data = xtdata.get_market_data_ex(['open','high','low','close','volume','amount','preClose','suspendFlag'],[code],period=period,start_time=start_date,count=count,dividend_type=dividend_type)
    df = history_data[code]

    df.index = pd.to_datetime(df.index.astype(str), format='%Y%m%d')
    df['date'] = df.index
    return df


def plot_fibonacci(df, period=200):
    """
    计算并绘制斐波那契回撤线
    :param df: DataFrame, 包含['open','high','low','close','volume']
    :param period: 回看区间长度，默认200
    """
    df = df.tail(period).copy()
    
    # 找高低点及索引
    high_idx = df['close'].idxmax()
    low_idx = df['close'].idxmin()
    high = df.loc[high_idx, 'close']
    low = df.loc[low_idx, 'close']
    
    # 判断谁更靠近最新K线
    last_idx = df.index[-1]
    if abs(last_idx - high_idx) < abs(last_idx - low_idx):
        # 高点更近：从高到低画线
        trend = "down"
    else:
        # 低点更近：从低到高画线
        trend = "up"
    
    # 计算斐波那契回撤
    diff = high - low
    levels = [0.236, 0.382, 0.5, 0.618, 0.786]
    fibo_levels = {}
    
    if trend == "down":
        fibo_levels = {f"{p*100:.1f}%": high - diff * p for p in levels}
    else:
        fibo_levels = {f"{p*100:.1f}%": low + diff * p for p in levels}
    
    
    # 绘图
    plt.figure(figsize=(12,6))
    plt.plot(df['close'].values, label="Close Price", color="black")
    
    begin_line = high if trend == "down" else low
    
    plt.hlines(begin_line, 0, len(df), linestyles="--",colors='red', label=f"begin_line: {begin_line:.2f}")
    plt.text(len(df)*0.99, begin_line, f"{begin_line:.2f}", va="center", ha="right", color="blue")
    
    # 画斐波那契水平线并标注价格
    for k, v in fibo_levels.items():
        if k == "61.8%":
            plt.hlines(v, 0, len(df), linestyles="--", colors='gold', label=f"{k}: {v:.2f}")
            plt.text(len(df)*0.99, v, f"{v:.2f}", va="center", ha="right", color="blue")
        else:
            plt.hlines(v, 0, len(df), linestyles="--", colors='gray', label=f"{k}: {v:.2f}")
            plt.text(len(df)*0.99, v, f"{v:.2f}", va="center", ha="right", color="blue")
        
   
    # 标记高点和低点
    plt.scatter(df.index.get_loc(high_idx), high, color="red", marker="o", s=100, label=f"High: {high:.2f}")
    plt.scatter(df.index.get_loc(low_idx), low, color="red", marker="o", s=100, label=f"Low: {low:.2f}")
    
    plt.title(f"Fibonacci Retracement ({trend}) - {period} bars")
    plt.legend()
    plt.show()
    
    return {
        "trend": trend,
        "high": (high_idx, high),
        "low": (low_idx, low),
        "fibo_levels": fibo_levels
    }

if __name__ == "__main__":
    df = get_hq('600519.SH', start_date='20220101', period='1d', dividend_type='front_ratio', count=200)
    result = plot_fibonacci(df, period=200)
    print(result)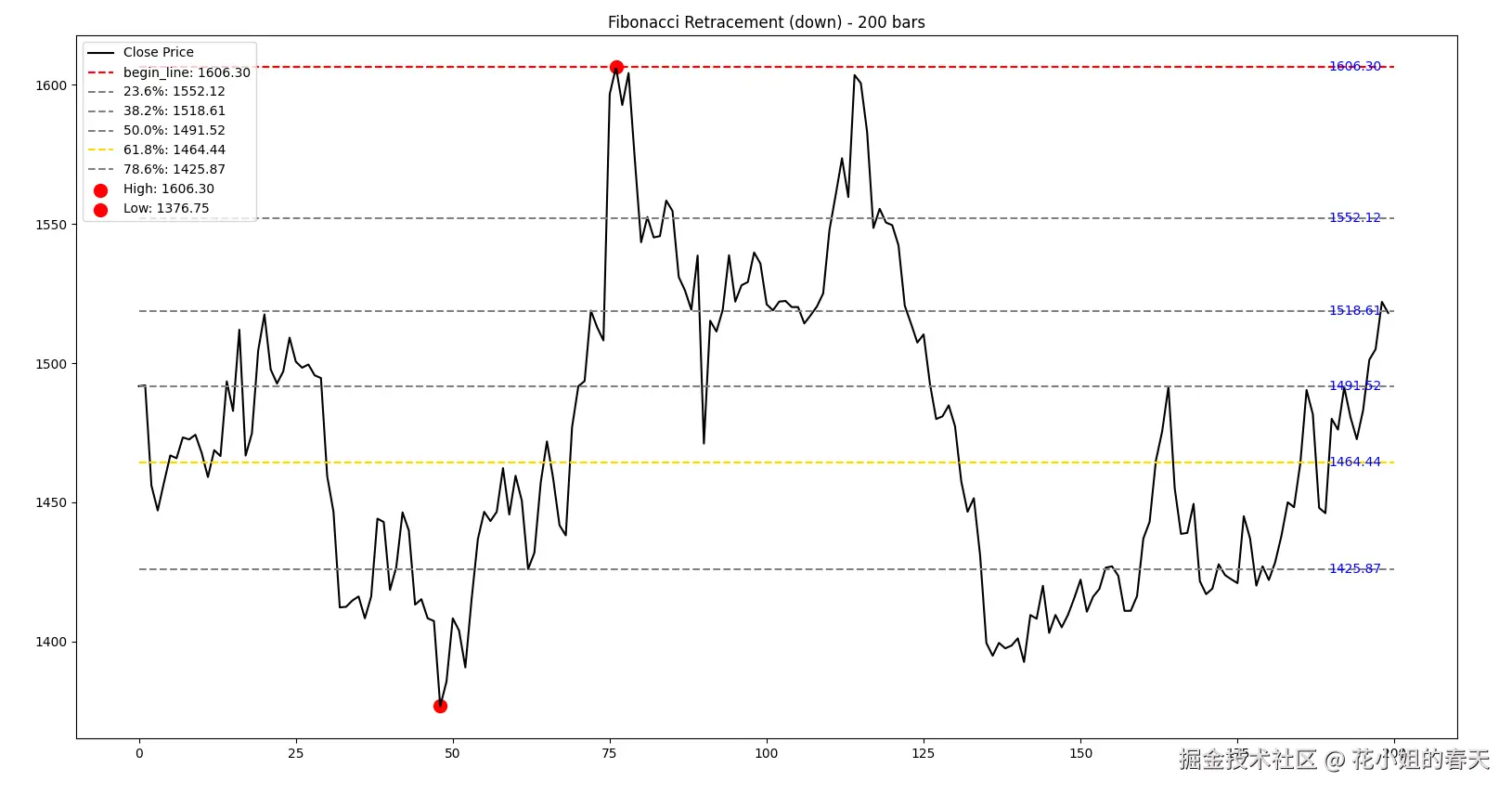

运行后你会得到一组价位，这些就是对应区间的斐波那契支撑/压力参考。

五、实战应用与注意事项

应用场景

辅助判断买入点：比如股价回调到0.618位置，可以观察是否企稳。
辅助判断止盈点：上涨过程中，0.382、0.5位置可能成为压力区域。

注意事项

斐波那契回撤不是万能指标，它只是市场心理的参考。
这些点位更像是一个"区间"，而不是绝对精准的价格点。💡
最佳做法是结合K线形态、均线、成交量等指标一起使用。

今天关于寻找股票支撑与压力位的斐波那契法就写到这里了，更高级的用法有兴趣的朋友可以结合AI来自由探索，花姐这里只做简单科普抛砖引玉。

下一篇我们介绍通过成交量剖面寻找股票支撑与压力位。