截止9.21周日20:00已更新问题一二的完整代码和文章
完整内容请看文末的名片获取哦
总体建模思路与框架
本赛题的核心是构建一个基于迁移学习的智能故障诊断系统,旨在解决实际工程中目标域(在途列车)故障数据稀缺的难题。其基本思路是:首先在数据丰富、标签完备的源域(试验台数据)上构建一个高性能的故障诊断模型;随后,利用迁移学习技术,将该模型所学到的关于轴承故障的通用知识(如故障特征表示、分类决策边界)适配到数据分布不同但任务相似的目标域上,最终实现对目标域未知状态轴承的精准诊断。整个建模过程将遵循"数据预处理与特征提取 -> 源域模型构建 -> 跨域迁移诊断 -> 模型可解释性分析"的逻辑链条。
在 MATLAB 中加载:
matlab
load('A.mat');
然后使用 whos 查看包含的变量名和大小。
在 Python 中加载:
使用 scipy.io.loadmat:
python
import scipy.io as sio
data = sio.loadmat('A.mat')print(data.keys()) # 查看变量名
问题一(轴承故障特征分析与提取)基于信号处理和特征工程的故障诊断特征提取管道
🧠 一、模型总览:多层级特征提取框架
该模型是一个基于滑动窗口的信号处理与特征工程管道,核心思想是从原始振动信号中提取能够区分不同故障类型(内圈IR、外圈OR、滚动体B、正常N)的判别性特征。整个流程如下图所示:
二、核心模块详细说明
-
数据预处理与标准化 (Preprocessing)
目的:将不同来源的原始信号统一到相同标准,为特征提取做准备。
重采样 (Resampling):将所有数据统一重采样至 TARGET_FS = 12 kHz,消除采样率差异(如12k vs 48k)。
带通滤波 (Bandpass Filtering):使用 butterworth 滤波器进行带通滤波(500-5000 Hz),保留轴承故障特征最丰富的频段,抑制低频和高频噪声。
滑动窗口分割 (Windowing):将长信号分割为固定时长(WINDOW_SEC = 1.0秒)的重叠窗口(OVERLAP = 50%),增加样本量,并捕获信号的局部特性。
-
多域特征提取 (Multi-Domain Feature Extraction)
这是模型的核心,旨在从不同角度全面描述信号状态。
a) 时域特征 (Time-Domain Features)
直接从时域信号波形中提取的统计特征,对冲击类故障敏感。
有量纲指标:RMS_raw, STD_raw, Peak_raw, PTP_raw (峰峰值)
无量纲指标(对载荷和转速变化不敏感):
峭度 (Kurtosis):衡量信号分布的尖锐程度,对冲击异常高度敏感。
偏度 (Skewness):衡量信号分布的不对称性。
峰值因子 (Crest Factor):Peak / RMS,用于检测冲击。
脉冲因子 (Impulse Factor):Peak / Mean(Abs)。
形状因子 (Shape Factor):RMS / Mean(Abs)。
裕度因子 (Clearance Factor):Peak / (Mean(Sqrt(Abs)))^2。
b) 频域特征 (Frequency-Domain Features)
对信号进行FFT变换后,从功率谱中提取的特征,反映信号的频率结构。
频谱中心 (Spectral Centroid):频谱的"重心"频率,反映能量集中的频带。
频谱散度 (Spectral Spread):频谱围绕中心的分散程度。
频谱熵 (Spectral Entropy):衡量频谱的混乱程度,熵值越低,说明能量越集中。
最大频率 (SpecMaxFreq):功率谱中最大分量对应的频率。
c) 包络谱与故障机理特征 (Envelope Spectrum & Fault Mechanism Features)
这是区分故障类型最关键的特征集。其物理原理是:轴承局部故障会产生周期性冲击,调制在高频共振频段上。包络分析(希尔伯特变换+频谱分析)能解调出冲击的频率,即故障特征频率。
计算包络谱:
对滤波后信号进行希尔伯特变换,得到包络线信号 env。
对 env 做FFT,得到包络谱 Es。
计算故障特征频率:根据轴承几何参数 (GEOM) 和估计的转速 (rpm),理论计算三种故障的特征频率:
BPFO (外圈故障频率)
BPFI (内圈故障频率)
BSF (滚动体故障频率)
FTF (保持架故障频率)
提取能量特征:
E_BPFO, E_BPFI, E_BSF:计算各特征频率前 K_HARM=5 次谐波在包络谱上的能量总和(考虑带宽 BW_Hz=2.0Hz)。
E_*_R:上述能量与包络谱总能量的比值,归一化后更稳定。
构造机理指示因子:这些比值是强大的判别因子。
FI_IR = E_BPFI_R / (E_BPFO_R + E_BSF_R) → 内圈故障指示器
FI_OR = E_BPFO_R / (E_BPFI_R + E_BSF_R) → 外圈故障指示器
FI_B = E_BSF_R / (E_BPFO_R + E_BPFI_R) → 滚动体故障指示器
正常状态下,这些值均很低且相近;发生特定故障时,对应指标会显著升高。
d) 时频域特征 (Time-Frequency Features)
使用短时傅里叶变换(STFT)获取信号的时变频谱特性。
频带能量:计算特定频带(如0-30, 30-60, 60-120, 120-240, 240-300 Hz)在STFT上的能量总和 (TF_E_*)。
最大能量频率 (TF_MaxFreq):在整个时频谱上,能量最强的频率。
- 数据集构建与模型训练
特征标准化:使用 StandardScaler 对特征进行Z-score标准化,消除量纲影响,加速模型收敛。
分类器选择:
支持向量机 (SVM with RBF Kernel):作为主分类器,擅长处理高维特征和非线性问题。
随机森林 (Random Forest):用于辅助分析特征重要性。
模型评估:采用严谨的评估策略:
分层划分:train_test_split 保持类别比例。
交叉验证:5折分层交叉验证评估模型稳定性。
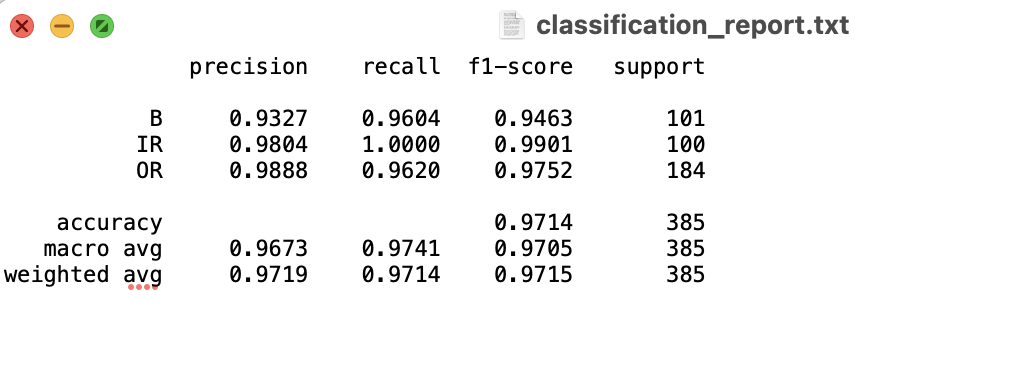
多维度评估指标:输出精确率、召回率、F1值、混淆矩阵、宏平均F1等。
高级评估:绘制ROC曲线、PR曲线、概率校准曲线,全面评估模型性能。
- 可解释性与可视化分析
代码包含了丰富的可视化模块,用于深入理解数据和模型:
数据分布:类别平衡性检查。
特征分析:特征相关性热图、箱线图(查看特征在不同类别上的区分度)。
模型决策:混淆矩阵、ROC/PR曲线、概率校准曲线。
深度洞察:
t-SNE可视化:将高维特征降至2维,直观观察不同故障类别的分离情况。
包络谱标记图:在包络谱上标注出理论故障频率及其谐波,直观验证特征提取的有效性。
特征重要性:基于随机森林分析哪些特征对分类贡献最大。
三、模型特点与优势
物理机理驱动:不是黑盒式特征提取,而是紧密结合轴承故障机理(特征频率),使得特征具有明确的物理意义,模型可解释性强。
多域融合:融合时域、频域、包络域、时频域特征,信息全面,能应对不同类型的故障模式。
对工况变化的鲁棒性:采用了无量纲指标、能量比值等特征,在一定程度上减弱了转速、载荷变化的影响。
四、输出结果
该模型最终输出:
一个包含所有提取特征的CSV文件 (source_features.csv)。
一个训练好的SVM分类模型。
问题二(源域故障诊断模型) 所建立的完整机器学习模型。这是在问题一特征工程基础上,构建的一个严谨、可泛化、高性能的故障分类系统。
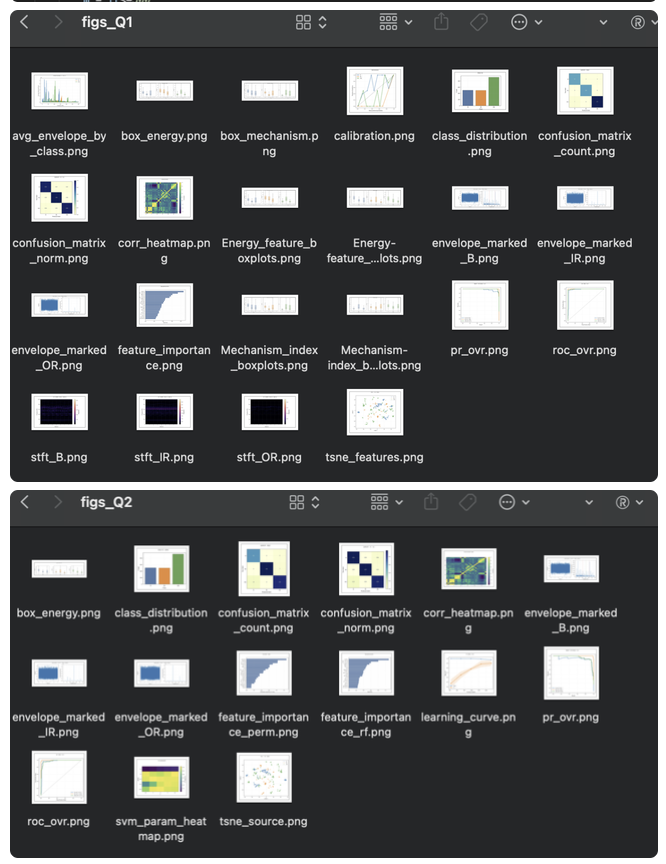
🧠 一、模型总览:面向泛化的诊断框架
问题二的核心目标是利用问题一提取的特征,在源域(试验台数据)上训练一个高精度、高泛化能力的故障诊断模型。其核心思想是:通过严格的组别划分防止数据泄漏,并系统化地优化和评估模型,确保其性能真实可靠。整个建模流程如下图所示: