【特殊函数】zeta函数

文章目录

[广义 zeta 函数的定义](#广义 zeta 函数的定义)
[zeta 函数的解析延拓](#zeta 函数的解析延拓)
[Riemann 猜想](#Riemann 猜想)
[sympy 包调用计算](#sympy 包调用计算)
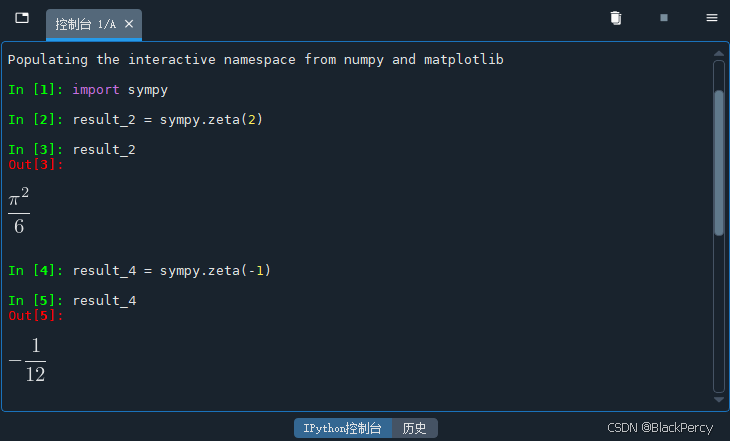
- [Spyder 中的运行结果](#Spyder 中的运行结果)

广义 zeta 函数的定义

ζ ( s , a ) = ∑ n = 0 ∞ ( n + a ) − s \zeta(s,a) = \sum_{n=0}^{\infty} (n+a)^{-s} ζ(s,a)=∑n=0∞(n+a)−s，其中 s s s, a a a 为复数， R e ( s ) > 1 \mathrm{Re}(s)>1 Re(s)>1， R e ( a ) > 0 \mathrm{Re}(a)>0 Re(a)>0

特殊情形 当参数 a = 1 a=1 a=1 时，广义Zeta函数退化为标准的Riemann Zeta函数 ：
ζ ( s ) = ∑ n = 1 ∞ n − s = ∏ p ∈ P 1 1 − p − s \zeta(s) = \sum_{n=1}^{\infty} n^{-s}=\prod_{p\in \mathbb{P}} \frac{1}{1-p^{-s}} ζ(s)=n=1∑∞n−s=p∈P∏1−p−s1

右侧称为欧拉无穷乘积，其中 P = { 2 , 3 , 5 , 7 , 11 , 13 , 17 , ⋯ } \mathbb{P}=\{2,3,5,7,11,13,17,\cdots\} P={2,3,5,7,11,13,17,⋯} 是所有素数（质数，除了自己与1没有其他正整数因子的正整数）的全体构成的集合。当 R e ( s ) > 1 Re(s) >1 Re(s)>1 时， ζ ( s ) \zeta(s) ζ(s) 是收敛级数。例如常见的有
ζ ( 2 ) = 1 1 2 + 1 2 2 + 1 3 2 + ⋯ = 2 2 2 2 − 1 3 2 3 2 − 1 5 2 5 2 − 1 7 2 7 2 − 1 11 2 11 2 − 1 ⋯ = π 2 6 . \zeta(2)= \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{2^2}{2^2-1}\frac{3^2}{3^2-1}\frac{5^2}{5^2-1}\frac{7^2}{7^2-1}\frac{11^2}{11^2-1}\cdots=\frac{\pi^2}{6}. ζ(2)=121+221+321+⋯=22−12232−13252−15272−172112−1112⋯=6π2.

zeta 函数的解析延拓

对 Riemann Zeta 函数在复平面上解析延拓后得到函数：

ζ ( s ) = 2 Γ ( 1 − s ) ( 2 π ) s − 1 sin ⁡ ( π s 2 ) ζ ( 1 − s ) , s ≠ 1 \zeta(s) = 2\Gamma(1-s) (2π)^{s-1} \sin\left(\frac{\pi s}{2}\right) \zeta(1-s), s\neq 1 ζ(s)=2Γ(1−s)(2π)s−1sin(2πs)ζ(1−s),s=1
s = 1 s=1 s=1 是唯一的奇点。解析延拓在量子力学中颇为常用，例如

ζ ( 0 ) = 1 + 1 + 1 + ⋯ = − 1 2 . \zeta(0) =1+1+1+\cdots = -\frac{1}{2}. ζ(0)=1+1+1+⋯=−21.
ζ ( − 1 ) = 1 + 2 + 3 + ⋯ = − 1 12 . \zeta(-1) =1+2+3+\cdots = -\frac{1}{12}. ζ(−1)=1+2+3+⋯=−121.

Riemann 猜想

解析延拓后，ζ函数具有两类零点：

平凡零点：这些零点出现在所有负偶数上，即 s = − 2 , − 4 , − 6 , ⋯ s = -2, -4, -6, \cdots s=−2,−4,−6,⋯。它们的性质简单，且分布有序。
非平凡零点：这些零点的实部都落在0到1之间的"临界带"内。黎曼在 1859 年提出了一个著名的猜想，即黎曼猜想：ζ函数的所有非平凡零点的实部都等于 1 2 \frac{1}{2} 21，也就是说，它们都位于复平面上 R e ( s ) = 1 2 Re(s)=\frac{1}{2} Re(s)=21 的这条"临界线"上。
黎曼猜想至今尚未被证明，但它对于理解素数的分布规律具有极其重要的意义。有超过一千条数学命题是建立在黎曼猜想成立的基础之上的。

sympy 包调用计算

python 复制代码

import sympy
# 计算 ζ(0)，通过解析延拓其值为 -1/2
result_0 = sympy.zeta(0)
print(result_0)  # 输出: -1/2
# 计算 ζ(-1)，解析延拓下的值是 -1/12
result_neg1 = sympy.zeta(-1)
print(result_neg1)  # 输出: -1/12

# 甚至可以尝试复数参数
s_complex = 0.5 + 2j
# 由于涉及复数，通常使用数值计算
complex_val = sympy.zeta(s_complex).evalf()
print(complex_val)  # 输出类似: 0.143936427078189 - 0.722099743531673*I