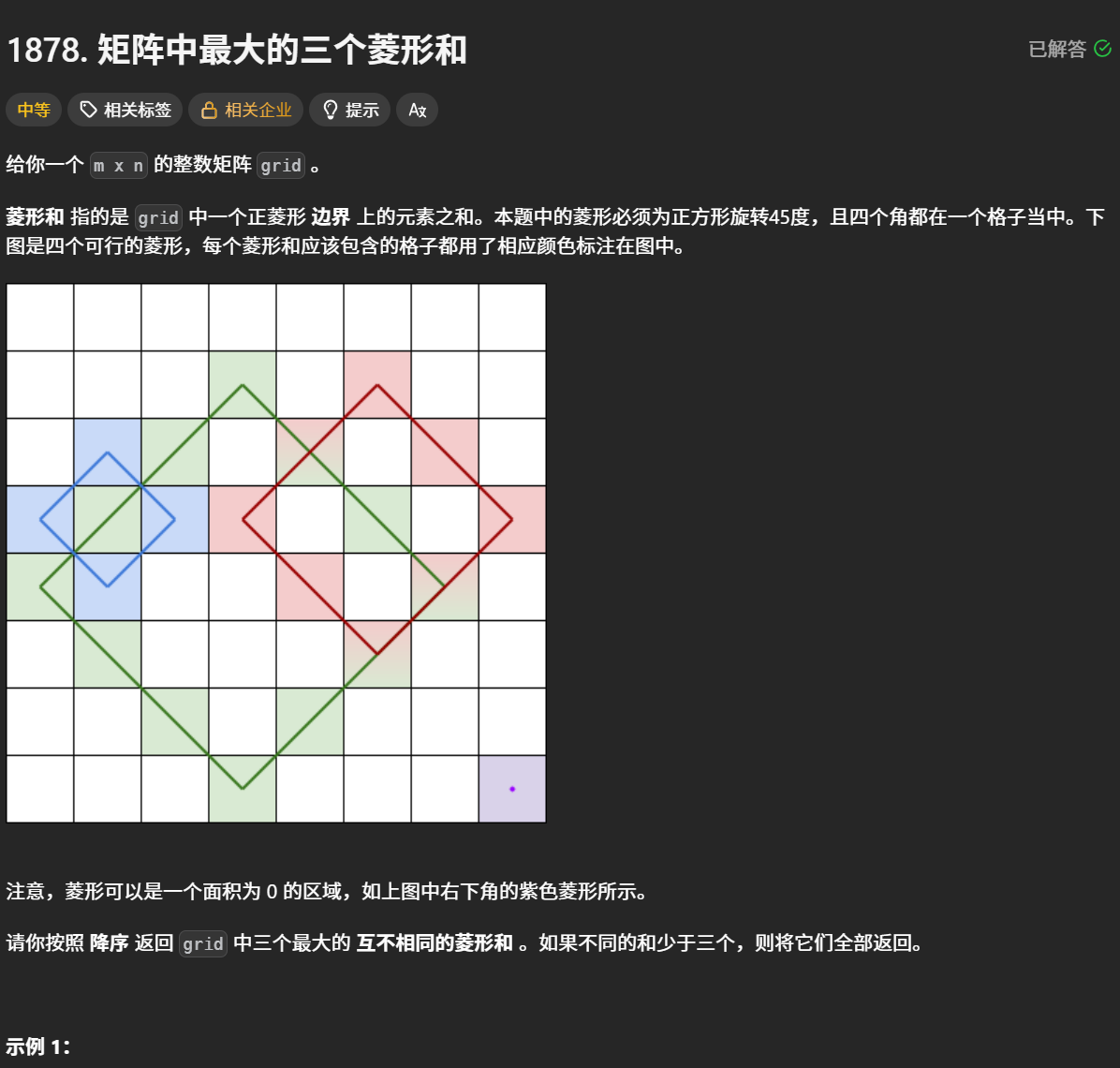
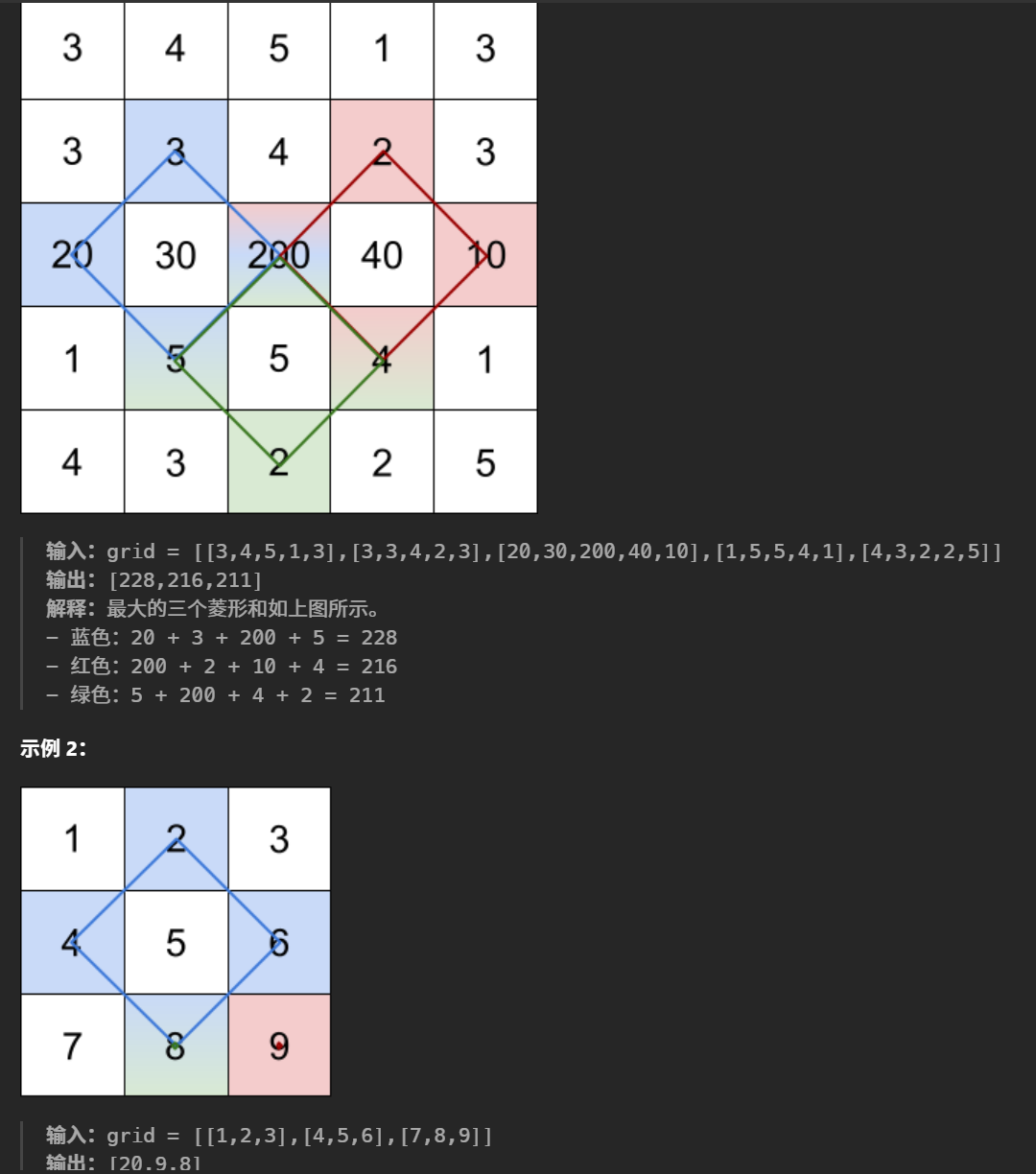

这一题的大意是指给出一个矩阵,里面的点可以构成菱形,这个菱形的特点是由正方形旋转45度构成的,菱形的面积也可以为0,那么它就可能是由一个单个的点构成。
现在让我们找在这个矩阵中,边长所经过的点的和最大的三个菱形。
我的思路是我们只需要枚举出来符合条件的菱形,然后计算各边之和放入数组中排序,即可得到点之和最大的三个菱形。
这实际上是类似在矩阵中枚举子矩阵的问题,无非是现在是来枚举菱形
类似题目:
因为这一题的数据范围比较小,只有10^2,所以可以大胆的尝试一下暴力:
枚举边长大约需要O(n),枚举矩阵中的所有点需要O(n^m)约等于O(n ^2),
在计算菱形上的所有点的和大概最长才为O(min(n,m)*4) 更何况大多数的边长情况,远远不能得到,因此是小于10^8的。
暴力写法事实也可以通过:
cpp
class Solution {
public:
static bool cmp(int a,int b)
{
return a>b;
}
vector<int> getBiggestThree(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
vector<int> ans;
vector<int> temp;
for(int edge=0;edge<min(n,m);edge++)
{
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
int x1=i;
int y1=j;
int x2=i+edge;
int y2=j-edge;
int x3=i+edge*2;
int y3=j;
int x4=i+edge;
int y4=j+edge;
if(x2>=m||y2<0||x3>=m||x4>=m||y4>=n)
{
continue;
}
int sum=0;
for(int x=x2,y=y2;x>=x1;x--,y++)
{
sum+=grid[x][y];
}
for(int x=x2+1,y=y2+1;x<=x3;x++,y++)
{
sum+=grid[x][y];
}
for(int x=x1+1,y=y1+1;x<=x4;x++,y++)
{
sum+=grid[x][y];
}
for(int x=x3-1,y=y3+1;x>=x4+1;x--,y++)
{
sum+=grid[x][y];
}
//cout<<sum<<endl;
ans.push_back(sum);
}
}
}
sort(ans.begin(),ans.end(),cmp);
int t;
for(int i=0;i<ans.size();i++)
{
if(i==0)
{
temp.push_back(ans[i]);
t=ans[i];
}
else if(t==ans[i])
{
continue;
}
else
{
temp.push_back(ans[i]);
t=ans[i];
}
if(temp.size()==3)
{
break;
}
}
return temp;
}
};也可以先枚举点,再枚举边,思路实际是一样的,代码写法有点差异
cpp
class Solution {
public:
static bool cmp(int a,int b)
{
return a>b;
}
vector<int> getBiggestThree(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
vector<int> ans;
vector<int> temp;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
//这是枚举了一个点
//现在我们要看从这个点可以引出怎么样的矩形
ans.push_back(grid[i][j]);
for(int k=1;k<min(m,n);k++)
{
//已知一个顶点和边长,自然可以推出这个菱形
int x1=i;
int y1=j;
int x2=i+k;
int y2=j-k;
int x3=i+2*k;
int y3=j;
int x4=i+k;
int y4=j+k;
if(y2<0||x3>=m||x4>=m||y4>=n)
{
break;
}
//当枚举出来矩阵后我们需要计算这个矩阵的值
int sum=0;
for(int x=x2,y=y2;x>=x1;x--,y++)
{
sum+=grid[x][y];
}
for(int x=x2+1,y=y2+1;x<=x3;x++,y++)
{
sum+=grid[x][y];
}
for(int x=x1+1,y=y1+1;x<=x4;x++,y++)
{
sum+=grid[x][y];
}
for(int x=x3-1,y=y3+1;x>=x4+1;x--,y++)
{
sum+=grid[x][y];
}
ans.push_back(sum);
}
}
}
sort(ans.begin(),ans.end(),cmp);
int t;
for(int i=0;i<ans.size();i++)
{
if(i==0)
{
temp.push_back(ans[i]);
t=ans[i];
}
else if(t==ans[i])
{
continue;
}
else
{
temp.push_back(ans[i]);
t=ans[i];
}
if(temp.size()==3)
{
break;
}
}
return temp;
}
};那么和在矩阵中枚举子矩阵一样,在计算边长的时候,我们可以用前缀和进行优化,提前算出边长,这样时间复杂度大概为O(n^3)一定可以过的。
但一般的前缀和是好求的,可这一题是菱形,菱形的边长是斜着的,因此用斜向的前缀和来求。
斜向前缀和怎么求的呢?
实际上就是求主对角线和副对角线的前缀和
也即求:
从左上到右下 ↘ 的前缀和
从右上到左下 ↙ 的前缀和
cpp
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
sum1[i][j]=sum1[i-1][j-1]+grid[i-1][j-1];
sum2[i][j]=sum2[i-1][j+1]+grid[i-1][j-1];
}
} 注意sum2数组的列要开大一点,因为在求从右上到左下的前缀和时,j+1可能会越界。
我们画画图就可以弄清楚:
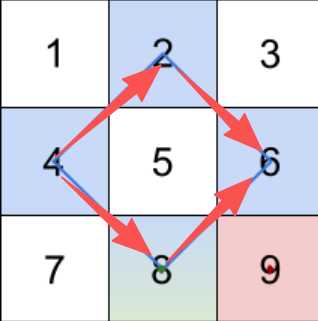
当我们知道怎么求前缀和之和,那么就可以把原来需要枚举的过程,用前缀和来表示,从而降低时间复杂度。
cpp
class Solution {
public:
static bool cmp(int a,int b)
{
return a>b;
}
vector<int> getBiggestThree(vector<vector<int>>& grid) {
int m=grid.size();
int n=grid[0].size();
vector<int> ans;
vector<int> temp;
vector<vector<int> > sum1(m+1,vector<int>(n+1+1,0));
vector<vector<int> > sum2(m+1,vector<int>(n+1+1,0));
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
sum1[i][j]=sum1[i-1][j-1]+grid[i-1][j-1];
sum2[i][j]=sum2[i-1][j+1]+grid[i-1][j-1];
}
}
for(int edge=0;edge<max(n,m);edge++)
{
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
int x1=i;
int y1=j;
int x2=i+edge;
int y2=j-edge;
int x3=i+edge*2;
int y3=j;
int x4=i+edge;
int y4=j+edge;
if(x2>=m||y2<0||x3>=m||x4>=m||y4>=n)
{
continue;
}
int sum=0;
if(edge==0)
{
ans.push_back(grid[i][j]);
continue;
}
else
{
sum+=sum2[x2+1][y2+1]-sum2[x1][y1+2];
sum+=sum2[x3+1][y3+1]-sum2[x4][y4+2];
sum+=sum1[x4+1][y4+1]-sum1[x1][y1];
sum+=sum1[x3+1][y3+1]-sum1[x2][y2];
sum-=(grid[x1][y1]+grid[x2][y2]+grid[x3][y3]+grid[x4][y4]);
ans.push_back(sum);
}
}
}
}
sort(ans.begin(),ans.end(),cmp);
int t;
for(int i=0;i<ans.size();i++)
{
if(i==0)
{
temp.push_back(ans[i]);
t=ans[i];
}
else if(t==ans[i])
{
continue;
}
else
{
temp.push_back(ans[i]);
t=ans[i];
}
if(temp.size()==3)
{
break;
}
}
return temp;
}
};这里和暴力枚举的过程有不同的是,我们无法表示edge=0的情况,因为在该情况下,用前缀和计算时会有越界。因此我们需要把edge==0的情况单独讨论。
总结:
这一题还是典型的在矩阵中枚举"子矩阵"的一类问题,无非这里的子矩阵是菱形,在优化时需要用斜向前缀和,但思路都是类似的。
优化后的时间复杂度
O(n^3)