C语言 ——— 操作符

移位操作符

原码、反码、补码

正整数的原、反、补码

负整数的原、反、补码

总结

右移操作符

正整数右移

负整数右移

左移操作符

正整数左移

负整数左移
 按位操作符

[按位与操作符 - "&"](#按位与操作符 - "&")

[按位或操作符 - "|"](#按位或操作符 - "|")

[按位异或操作符 - "^"](#按位异或操作符 - "^")
结构成员访问操作符

结构体

["." - 结构体.成员名](#"." - 结构体.成员名)

["->" - 结构体指针->成员名](#"->" - 结构体指针->成员名)
表达式求值

隐式类型转换

算术转换

移位操作符

移位操作符主要包含两种：左移操作符 "<<"** 和 **右移操作符 ">>" 。需要明确的是，这两种操作符的操作对象并非整型数据的十进制数值，而是其在内存中存储的二进制位。

更关键的是，整型数据（尤其是有符号整型）在计算机内存中并非直接存储其 "原码"，而是以补码的形式存储 ------ 这是计算机为了统一处理正负数运算、避免符号位运算冲突而采用的底层规则。因此，移位操作符实际移动的，正是整型数据补码对应的二进制位。

也正因为如此，要真正理解移位操作符的运算逻辑（比如移位后数值如何变化、符号位是否参与移动等），就必须先掌握 "原码、反码、补码" 的概念与转换规则。毕竟移位操作是直接作用于补码的底层位运算，若不了解补码的存储逻辑，很容易对移位后的结果产生误解，甚至出现计算错误（例如误判负数移位后的符号或数值）。

原码、反码、补码

正整数的原、反、补码

代码演示：

复制代码

int a = 15;

定义变量 a 为 int 整型 ，这意味着它在内存中占用 4 字节（即 32 位）的存储空间，且被赋值为正整数 15。

在计算机中，无论是正整数还是负整数，其原码都可直接由数值本身的二进制形式推导得出 ------ 但需注意，原码的位数必须与变量的数据类型所规定的存储位数一致。由于 a 是 int 类型（4 字节 = 32 位），即便 15 的有效二进制形式（1111）仅占 4 位，也需要在前面补全足够的 0，以填满 32 位的存储长度。

此外，二进制原码的 最高位（即第 31 位，从 0 开始计数）是符号位，这是计算机区分正负数的核心标识：

当符号位为 0 时，代表该数值是 正整数；
当符号位为 1 时，代表该数值是 负整数。

且在计算机对整型数据的编码规则中，有一个关键特性：正整数的原码、反码、补码三者完全相同，这是正整数与负整数在二进制编码上最显著的区别之一。

因此，正整数 15 对应的原码需满足 "32 位长度 + 符号位为 0" 的要求，最终其原、反、补码表现形式统一为：
00000000 00000000 00000000 00001111

这里补充一点：补全前导 0 并非多余操作，而是为了符合 int 类型的固定存储规范 ------ 计算机对不同数据类型的内存占用有严格规定，4 字节的 int 必须以 32 位二进制形式存储，确保内存空间分配的一致性；而符号位的设计，则让二进制序列既能承载数值大小信息，又能明确数值的正负属性，是计算机实现正负数值运算的基础。

负整数的原、反、补码

代码演示：

复制代码

int a = -15;

与正整数 "原、反、补码三者相同" 的特性不同，负整数的原码、反码、补码必须通过特定规则逐步计算，核心差异集中在符号位和数值位的处理上

-15 的原码：

负整数的原码规则与正整数一致 ------ 数值位对应该数绝对值的二进制形式，唯一区别是最高位（符号位）必须为 1（用于标识负数，正整数符号位为 0）。

得出 -15 的原码为：10000000 00000000 00000000 00001111

-15 的反码：

原码转反码的核心规则是："符号位保持不变，其余所有数值位按位取反"（"按位取反" 指二进制位的 0 变为 1，1 变为 0）。

得出 -15 的反码为：11111111 11111111 11111111 11110000

-15 的补码：

反码转补码的规则非常明确："在反码的基础上整体加 1"（若加 1 后产生进位，需向高位依次传递，直至进位消除，这里 -15 的反码末尾为 0，无需复杂进位）。

最终得出 -15 的补码为：11111111 11111111 11111111 11110001

总结

基本概念：三者是计算机表示整型数据的三种二进制编码形式，核心作用是统一正负整数的运算逻辑，尤其是让减法可通过加法实现。
正整数特性 ：原码、反码、补码完全相同。
- 原码：符号位（最高位）为 0，数值位是该数的二进制形式（不足类型位数时补 0）；
- 示例：15（int 型）的三种码均为 00000000 00000000 00000000 00001111。
负整数规则：三种码需分步计算，且互不相同：
- 原码：符号位为 1，数值位是该数绝对值的二进制形式；
- 反码：符号位不变，其余数值位按位取反；
- 补码：反码基础上加 1；
- 示例：-15（int 型）的原码为 10000000...00001111，反码为 11111111...11110000，补码为 11111111...11110001。
关键结论 ：计算机内存中实际存储的是补码，所有位运算（如移位、按位操作）均基于补码进行，理解这一点是正确处理整型数据运算的基础。

右移操作符

正整数右移

代码演示：

复制代码

int a = 15;
int b = a >> 1;

printf("%d\n", a);
printf("%d\n", b);

1. 右移操作的基本特性

执行 a >> 1 时，是将变量 a 的二进制补码向右移动 1 位，原变量 a 的值不会发生改变 （右移操作仅产生新结果，不修改原变量），因此打印 a 时仍为初始值 15。新结果被赋值给 b，b 的值由右移后的二进制补码决定。

2. 右移的两种类型与 C 语言的选择

右移操作分为两种核心类型：

算术右移 ：右边的二进制位被直接丢弃，左边空缺的位补原来的符号位（保持符号不变）；
逻辑右移 ：右边的二进制位被直接丢弃，左边空缺的位统一补0（不考虑符号位）。

C 语言标准并未明确规定右移必须采用哪种方式，但绝大多数编译器对有符号整数默认使用算术右移，这是实际编程中需重点关注的规则。

3. 正整数 15 右移 1 位的具体过程

由于 a 是正整数 15（int 类型，4 字节），其补码与原码一致，为：
00000000 00000000 00000000 00001111（符号位为 0，代表正数）。

按算术右移规则处理：

右边最低位的 "1" 被丢弃；
左边空缺的位补原符号位（0）；

右移 1 位后得到的新补码为：
00000000 00000000 00000000 00000111，对应十进制数值 7。

因此，b 的值为 7，最终打印结果中 a=15、b=7。

负整数右移

代码演示：

复制代码

int a = -15;
int b = a >> 1;

printf("%d\n", b);

1. 负整数右移的前提：明确补码

负整数在内存中以补码形式存储，因此右移操作的对象是其补码。已知 -15（int 类型，4 字节）的补码为：11111111 11111111 11111111 11110001（符号位为 1，代表负数）。

2. 右移 1 位的具体过程（算术右移）

C 语言中多数编译器对负整数仍采用算术右移 ：右边最低位的二进制位被丢弃，左边空缺的位补原符号位（此处为 1，保持负数特性）。

对 -15 的补码右移 1 位后，得到的新补码为：11111111 11111111 11111111 11111000。

3. 从补码还原为原码：获取实际值

计算机存储的是补码，但 printf 打印的是数值的十进制真值，需将右移后的补码还原为原码：

步骤 1：补码减 1 得反码 新补码 11111111 11111111 11111111 11111000 减 1 后，得到反码：11111111 11111111 11111111 11110111。
步骤 2：反码取反（符号位不变）得原码 反码的数值位按位取反（符号位保持 1 不变），得到原码：10000000 00000000 00000000 00001000。

该原码对应的十进制数值为 -8，因此 b 的打印结果为 -8。

左移操作符

左移操作符（"<<"）的规则相比右移更为简洁且统一，无论操作对象是正整数还是负整数，其底层逻辑完全一致：

每次执行左移时，将整数的二进制补码整体向左移动指定的位数（如左移 1 位、左移 n 位），移动后：

右边空缺的位一律补 0（无论原数正负，补 0 规则不变）；
左边超出存储位数的高位直接被丢弃（例如 int 类型占 32 位，左移后第 32 位及以上的高位会被舍弃）。

举例来说，若对某个整数左移 1 位，就是将其二进制补码向左移 1 位，右边补 1 个 0，左边最高位丢弃 1 位；若左移 n 位，则重复这一过程 n 次 ------ 右边补 n 个 0，左边丢弃 n 个高位。

正整数左移

代码演示：

复制代码

int a = 6;
int b = a << 1;

printf("%d\n", b);

1. 正整数的补码特性

由于 a 是正整数 6（int 类型，4 字节），其原码、反码、补码完全一致，对应的二进制补码为：00000000 00000000 00000000 00000110（符号位为 0，数值位对应 6 的二进制形式）。

2. 左移 1 位的具体过程

左移操作符（<<）的规则对正整数和负整数完全统一：整体向左移动指定位数，右边空缺的位补 0，左边超出存储长度的高位直接丢弃。

对 6 的补码执行左移 1 位操作：

二进制序列整体左移 1 位，左边最高位的 "0" 被丢弃；
右边空缺的位置补 1 个 0；

最终得到的新补码为：00000000 00000000 00000000 00001100。

3. 结果解析

因正整数的补码与原码一致，新补码对应的十进制数值为 12，因此 b 的打印结果为 12。

负整数左移

负整数的左移与正整数的左移，在核心操作规则上完全一致------ 无论是正整数还是负整数，执行左移时都遵循 "将二进制序列整体左移指定位数，右边空缺位一律补 0，左边超出变量存储长度的高位直接丢弃" 的逻辑，不存在因数值正负而改变的特殊规则。

二者的唯一区别仅在于负整数需要额外处理 "补码的转换与还原" ：由于计算机内存中存储的负整数是补码（而非原码），因此对负整数执行左移前，必须先根据负整数的原码算出其对应的补码；左移操作直接作用于这份补码（操作过程与正整数操作补码完全相同）；但左移后得到的结果仍是 "补码形式"，而 printf 打印的是数值的十进制真值，因此还需将左移后的补码反向还原为原码，才能得到最终要打印的结果。

反观正整数，因其原码、反码、补码三者完全相同，无需额外的 "补码计算" 和 "补码还原原码" 步骤，左移后直接用补码（即原码）即可得到十进制结果 ------ 但这并非左移规则不同，只是正整数的编码特性省去了转换环节。

按位操作符

按位操作符有：按位与操作符 - "&"，按位或操作符 - "|"，按位异或操作符 - "^"

注意：以上操作符的操作数必须是整数，且操作符操作的是整数的补码

按位与操作符 - "&"

规则：

对两个操作数相同位置的二进制位逐一进行判断，只要其中任意一个位为 0，该位置的运算结果就为 0 ；只有当两个操作数对应位置的二进制位同时为 1 时，运算结果的该位置才会是 1。

简单来说，按位与的逻辑可理解为 "同 1 则 1，有 0 则 0"，且运算仅作用于二进制位，不直接处理十进制数值。

代码演示：

复制代码

int a = 3;
int b = -5;
int c = a & b;

printf("%d\n", c);

3 的补码为：00000000 00000000 00000000 00000011

-5 的补码为：11111111 11111111 11111111 11111011

按位于结果为：00000000 00000000 00000000 00000011

运算结果的补码符号位为 0（正整数），因此补码与原码一致，对应的十进制数值为 3。综上，printf("%d\n", c); 最终打印的结果是 3。

按位或操作符 - "|"

规则：

对两个操作数相同位置的二进制位逐一判断，只要其中任意一个位为 1，该位置的运算结果就为 1 ；只有当两个操作数对应位置的二进制位全为 0 时，运算结果的该位置才是 0。

简单来说，按位或的逻辑是 "有 1 则 1，全 0 才 0"

代码演示：

复制代码

int a = 3;
int b = -5;
int c = a | b;

printf("%d\n", c);

3 的补码为：00000000 00000000 00000000 00000011

-5 的补码为：11111111 11111111 11111111 11111011

按位或结果为：11111111 11111111 11111111 11111011

运算结果的补码符号位为 1（负整数），需反向转换为原码：

补码减 1 得反码 ：11111111 11111111 11111111 11111010；
反码取反（符号位不变）得原码 ：10000000 00000000 00000000 00000101；

该原码对应的十进制数值为 -5，因此 printf("%d\n", c); 最终打印的结果是 -5。

按位异或操作符 - "^"

规则：

对两个操作数相同位置的二进制位逐一判断，若对应位的数值相同（均为 0 或均为 1），则运算结果的该位置为 0；若对应位的数值不同（一个为 0、一个为 1），则运算结果的该位置为 1。

简单来说，按位异或的逻辑是 "同 0 异 1"------ 它关注的是二进制位的 "差异"

代码演示：

复制代码

int a = 3;
int b = -5;
int c = a ^ b;

printf("%d\n", c);

3 的补码为：00000000 00000000 00000000 00000011

-5 的补码为：11111111 11111111 11111111 11111011

按位异或结果为：11111111 11111111 11111111 11111000

运算结果的补码符号位为 1（表示负整数），需反向转换为原码才能得到十进制真值：

补码减 1 得反码 ：11111111 11111111 11111111 11110111；
反码取反（符号位不变）得原码 ：10000000 00000000 00000000 00001000；

该原码对应的十进制数值为 -8，因此 printf("%d\n", c); 最终打印的结果是 -8。

结构成员访问操作符

要理解结构成员访问操作符，首先需要明确其作用对象 ------结构体 的本质：结构体是 C 语言中的一种复杂类型 ，同时也是自定义类型 ，它允许开发者将多个不同基础类型（如int、char、float等）的变量 "封装" 在一起，形成一个统一的 "数据集合"，用于描述具有多属性的复杂对象（比如用结构体描述 "学生"，包含学号、姓名、成绩等成员）。

而结构成员访问操作符的核心作用，就是 "定位并访问" 结构体内部的某个具体成员，它包含两种形式：

"." 操作符 ：语法格式为 "结构体变量。成员名"，适用于直接通过结构体变量访问其成员；
"->" 操作符 ：语法格式为 "结构体指针。成员名"，适用于通过指向结构体的指针访问其成员。

这两个操作符的使用逻辑完全依赖于结构体的定义 ------ 如果不先理解 "结构体如何定义""它包含哪些成员""成员的类型是什么"，就无法正确使用这两个操作符定位成员。简单来说，结构体是 "容器"，成员是 "容器里的物品"，而 "." 和 "->" 就是打开容器、取出对应物品的 "工具"，没有对 "容器"（结构体）的认知，"工具"（操作符）就失去了使用意义。

结构体

代码演示：

复制代码

struct Book
{
	char name[30];    //书名
	char author[20];  //作者
	float price;      //价格
};

int main()
{
	struct Book b1 = { "C语言","张三",45.5 };
	struct Book b2 = { "数据结构","李四",65.5 };

	return 0;
}

1. 结构体类型定义：struct Book

定义了一个名为 Book 的结构体类型（struct 是结构体的关键字），它包含三个不同类型的成员（即结构体内部的 "属性"）：

char name[30]：字符数组，用于存储书名（最多 30 个字符，适配中文书名等场景）；
char author[20]：字符数组，用于存储作者名（最多 20 个字符）；
float price：单精度浮点型，用于存储书籍价格。

这个定义的本质是 "创建了一个新的自定义类型"------struct Book 就像 int、float 一样，是一种可以用来定义变量的类型，只不过它描述的是 "具有多个关联属性的复杂对象"（这里是 "书"）。

2. main 函数中的结构体变量创建与初始化

在 main 函数中，基于 struct Book 类型创建了两个结构体变量 b1 和 b2，并通过初始化列表为它们的成员赋值：

struct Book b1 = { "C语言","张三",45.5 };：变量 b1 被初始化为一本名为《C 语言》、作者为 "张三"、价格 45.5 的书。初始化时，值的顺序与结构体成员定义的顺序严格对应（第一个值对应 name，第二个对应 author，第三个对应 price）。
struct Book b2 = { "数据结构","李四",65.5 };：变量 b2 被初始化为一本名为《数据结构》、作者为 "李四"、价格 65.5 的书，初始化逻辑与 b1 一致。

"." - 结构体.成员名

复制代码

struct Book b1 = { "C语言","张三",45.5 };

printf("书名：%s，作者：%s，价格：%f", b1.name, b1.author, b1.price);

"->" - 结构体指针->成员名

复制代码

void Print(struct Book* pb)
{
	printf("书名：%s，作者：%s，价格：%f\n", pb->name, pb->author, pb->price);
}

int main()
{
	struct Book b1 = { "C语言","张三",45.5 };

	Print(&b1);

	return 0;
}

表达式求值

表达式求值的顺序一部分是由操作符的优先级和综合性决定的

同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型

隐式类型转换

C语言的整型算术运算总是至少以缺省整型类型的精度来进行的

为了获得这个精度，表达式中的字符和短整型操作数在使用之前会被转换为普通整型（int），这种转换称为整型提升

代码演示：

复制代码

char a = 5;
char b = 127;
char c = a + b;

printf("%d\n", c);

1. 变量定义与初始补码

代码中定义了三个char类型变量：a=5、b=127、c（用于接收a+b的结果）。char类型通常占1 字节（8 位），且默认是有符号类型（范围为 - 128~127），其初始补码为：

a=5（正数，符号位为 0）：8 位补码为 00000101；
b=127（正数，符号位为 0）：8 位补码为 01111111（127 是有符号 char 的最大值）。

2. 运算前的 "整型提升"

C 语言规定：小于int类型的整型（如char、short）在参与运算时，会先自动提升为int类型 （通常 4 字节，32 位），目的是避免运算过程中的精度损失。提升规则为：按原类型的符号位（最高位）补全高位，直至扩展为 32 位：

a的符号位是 0（正数），提升后 32 位补码为：00000000 00000000 00000000 00000101；
b的符号位是 0（正数），提升后 32 位补码为：00000000 00000000 00000000 01111111（注：原描述中b的补码多写了 1 位，正确应为 8 位01111111，提升后 32 位如左）。

3. a + b的运算结果

提升为int类型后，二者相加的 32 位结果为：00000000 00000000 00000000 00000101（a） + 00000000 00000000 00000000 01111111（b） = 00000000 00000000 00000000 10000100，对应十进制 132。

4. 赋值给c时的 "数据截断"

由于c是char类型（仅 8 位），32 位的运算结果会被截断 ------ 只保留最低 8 位，高位 24 位被丢弃，因此c的 8 位补码为：10000100（此时符号位为 1，说明c已变为负数）。

5. 打印时的再次 "整型提升" 与结果还原

printf("%d\n", c)中，%d要求参数为int类型，因此c会再次进行整型提升：

c的 8 位补码是10000100（符号位为 1），按符号位补全 32 位后，补码为：11111111 11111111 11111111 10000100。

要得到十进制结果，需将补码还原为原码：

补码减 1 得反码：11111111 11111111 11111111 10000011；
反码符号位不变，其他位取反得原码：10000000 00000000 00000000 01111100，对应十进制 **-124**。

所以最后 printf("%d\n", c); 打印的结果是 -124

算术转换

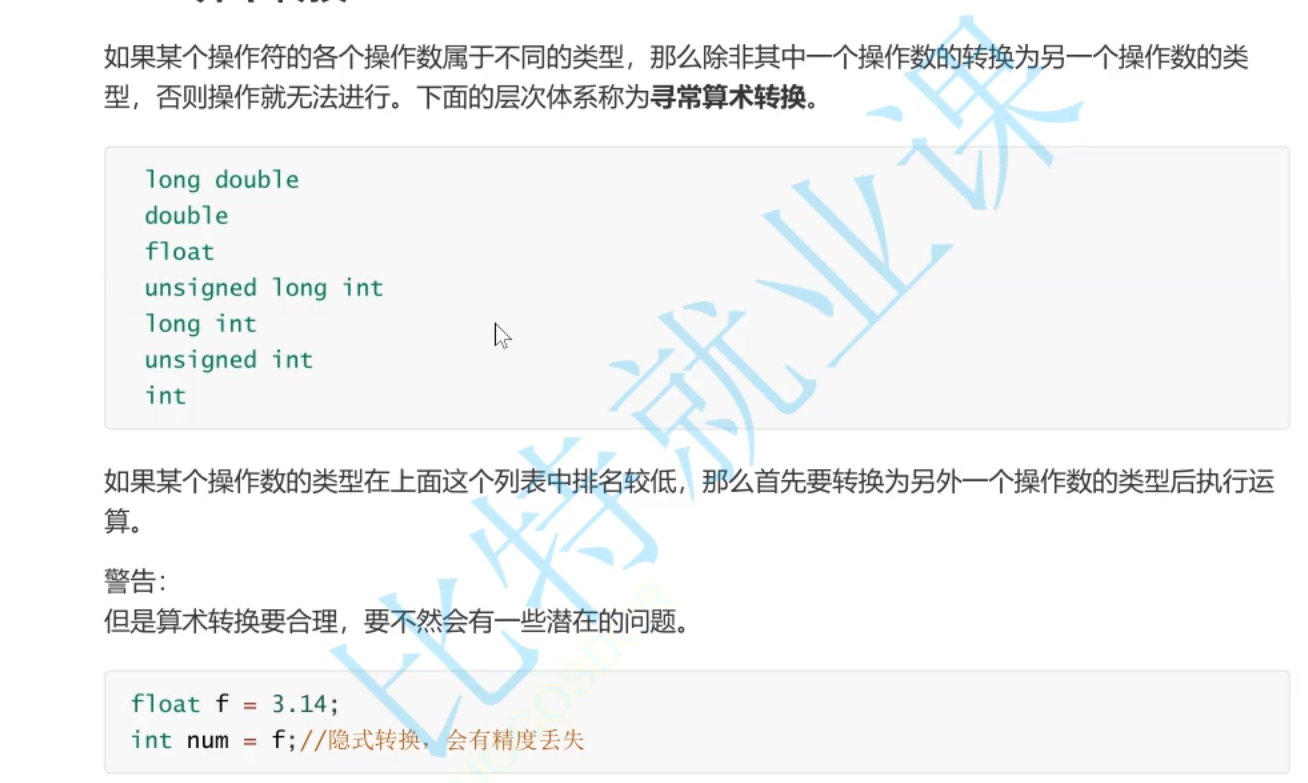
如果某个操作符的各个操作数量属于不同的类型，那么除非其中一个操作数转换位另一个操作数的类型，否则操作就无法进行

复制代码

long double;
double;
float;
unsigned long int;
long int;
unsigned int;
int;

以上数据类型都是向上提升的，如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算

C语言 ——— 操作符

目录

移位操作符

原码、反码、补码

正整数的原、反、补码

负整数的原、反、补码

总结

右移操作符

正整数右移

负整数右移

左移操作符

正整数左移

负整数左移

按位操作符

按位与操作符 - "&"

按位或操作符 - "|"

按位异或操作符 - "^"

结构成员访问操作符

结构体

"." - 结构体.成员名

"->" - 结构体指针->成员名

表达式求值

隐式类型转换

算术转换