概述
上一篇文章 解析了多层感知机（Multi-Layer Perceptron）模型的输入空间划分（Space Partitioning）与编码逻辑，本章将解析卷积神经网络（Convolutional Neural Networks，CNN）或简称卷积网络的模型运行逻辑。卷积网络本身是多层感知机的推广，即基于局部MLP的神经网络。
超立方体与归一化
我们在处理或预处理数据的时候，都会将输入数据限制到一个特定的范围，如将图像的数据采样到 0~255 的值、将输入归一化到 [ − 1 , 1 ] [-1,1] [−1,1]等等。当我们使用这样的数据时，任意的数据都等价于来自超立方体（hypercube）的点采样。如：对于 [ 100 × 100 × 3 ] [100\times 100\times 3] [100×100×3]的任意图片数据，其每个像素点的值为0~255的整数，我们总能找到在维度为30000，每维坐标轴范围为[0,255]的超立方上的点与其对应。
所以在机器学习中，我们将这样的来自超立方体的点采样分类，本质也是在将超立方空间划分为多个子空间。比如我们可以使用一个n-1维的分离超平面将n维超立方体划分为两个子空间（子超立方体）。限制输入空间为n维的超立方，比直接划分n维无范围限制的空间更直观，而实际上我们也是这么做的，不然为何我们要将输入归一化呢。
所以，分类的本质就是研究如何将数据空间的划分，当输入空间被确定的超平面排列划分时，那么各子空间数据的类别就被确定了。
局部的空间划分
卷积网络隐藏层对局部输入空间的划分方式与MLP的隐藏层是完全一致的，对于任意的局部输入都有
y = R e L U ( w T x + b ) y=ReLU(w^\mathsf{T}x+b) y=ReLU(wTx+b)如下图中，任意的卷积操作即逐点相乘，都可以转换为矩阵乘的形式，只需将卷积核及对应的输入展开为 [ 1 × n ] [1\times n] [1×n] 与 [ n × 1 ] [n\times 1] [n×1]的矩阵即可，当输入为多通道(Channels)也是完全一样的，只是参数多少的问题。
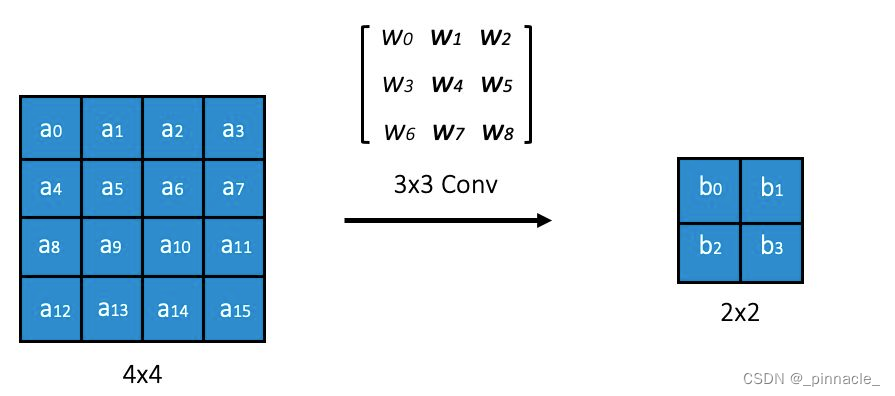所以对于任意的局部空间，我们都可以沿用MLP的空间划分逻辑。对于 K K K个卷积核的隐藏层而言，其神经元数量或节点数就是 K K K，将任意的局部输入空间划分为最大 ∑ i = 0 d C m i \sum_{i=0}^{d}C_m^i ∑i=0dCmi个线性区域(Linear Regions)，其中 d d d为输入空间维度； m m m为隐藏层节点数。
卷积网络中的子结构
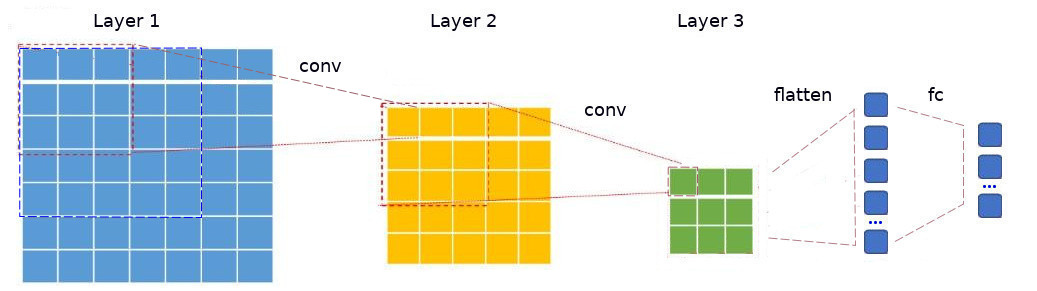
以前说过，CNN本质上是MLP网络的推广，这节将做一些拆解工作。以前的章节中已经解释了，全连接FC与多层感知机MLP的空间划分原理，所以这里FC本质是将输入的特征空间(Feature Space)划分到K个区域，且每个区域对应一个类别数据，所以FC层的逻辑是比较简单的。
在CNN中感受野(Receptive Field)是一个非常重要的概念，感受野是指特征图上的某个特征点能观测到的输入图像的局部区域。如上图中虚线圈内(绿色)格点对应的第一层输入层的(蓝色虚线)区域（conv size=3x3,stride=1），就是该格点的感受野。而其从该特征点到其关联输入图像区域的拓扑结构，构成CNN的一个子网络 。为了更清晰的表示网络结构，这里定义：
⋃ i = 1 n x i = C o n c a t ( x 1 , x 2 , . . . , x n ) {\bigcup_{i=1}^{n}x_i} =Concat(x_1,x_2,...,x_n) i=1⋃nxi=Concat(x1,x2,...,xn) Γ ( x ) = F l a t t e n ( x ) \Gamma (x) = Flatten(x) Γ(x)=Flatten(x)其中Concat为多个输入连接为向量，Flatten为 [ m × n ] [m\times n] [m×n]矩阵展开为 [ m n × 1 ] [mn\times 1] [mn×1]的矩阵，那么该子网络(橙色 ⇒ \Rightarrow ⇒绿色 )任意格点可以用如下公式表示：
f ( x ) = R e L U ( w 2 T x + b 2 ) ) f(x)=ReLU(w_{2}^\mathsf{T}x+b_{2})) f(x)=ReLU(w2Tx+b2))其中 x x x为 [ 3 × 3 ] [3\times 3] [3×3]区域的展开，也可以得到(蓝色虚线区 ⇒ \Rightarrow ⇒橙色 )
x = R e L U ( Γ ( [ w 1 T x 1 1 + b 1 ⋯ w 1 T x 1 3 + b 1 ⋯ ⋯ ⋯ w 1 T x 3 1 + b 1 ⋯ w 1 T x 3 3 + b 1 ] ) ) x=ReLU(\Gamma (\begin{bmatrix} w_{1}^\mathsf{T}x_1^1+b_{1} & \cdots & w_{1}^\mathsf{T}x_1^3+b_{1} \\ \cdots & \cdots &\cdots \\ w_{1}^\mathsf{T}x_3^1+b_{1} & \cdots & w_{1}^\mathsf{T}x_3^3+b_{1} \end{bmatrix})) x=ReLU(Γ( w1Tx11+b1⋯w1Tx31+b1⋯⋯⋯w1Tx13+b1⋯w1Tx33+b1 ))其中任意的 x i j x_i^j xij也是 [ 3 × 3 ] [3\times 3] [3×3]区域的展开，所以：
f ( x ) = R e L U ( w 2 T R e L U ( [ w 1 T x 1 1 + b 1 ⋯ w 1 T x 3 3 + b 1 ] ) + b 2 ) ) f(x)=ReLU(w_{2}^\mathsf{T}ReLU(\begin{bmatrix} w_{1}^\mathsf{T}x_1^1+b_{1} \\ \cdots \\ w_{1}^\mathsf{T}x_3^3+b_{1} \end{bmatrix})+b_{2})) f(x)=ReLU(w2TReLU( w1Tx11+b1⋯w1Tx33+b1 )+b2))显然，这个就是标准的MLP结构，与普通MLP的区别是：参数共享、局部输入的聚合、多卷积核 。当将局部结构解析出来的时候，那么就可以按照MLP的原理进行解析了。同理在多组卷积核时，可以得到该子网络：
f ( x ) = R e L U ( ⋃ i = 1 m ( w i T R e L U ( [ ⋃ j = 1 n w j T x 1 1 + b j ⋯ ⋃ j = 1 n w j T x 3 3 + b j ] ) + b i ) ) ) f(x)=ReLU(\bigcup_{i=1}^{m}( w_{i}^\mathsf{T}ReLU(\begin{bmatrix} \bigcup_{j=1}^{n}w_{j}^\mathsf{T}x_1^1+b_{j} \\ \cdots \\ \bigcup_{j=1}^{n}w_{j}^\mathsf{T}x_3^3+b_{j} \end{bmatrix})+b_{i}))) f(x)=ReLU(i=1⋃m(wiTReLU( ⋃j=1nwjTx11+bj⋯⋃j=1nwjTx33+bj )+bi)))以前也谈过，反向传播算法(Back Propagation)本身是一个全局优化算法，它并不关心中间层如何表示，只关注最终结果指标，所以给上面的 f ( x ) f(x) f(x)加上FC分类层，再通过反向传播优化，其核心就是 MLP+BP ，通过以前的实验结果可以知道，中间层只是为分类层最终结果服务的，它也只是递归的空间划分中的一个小节点。
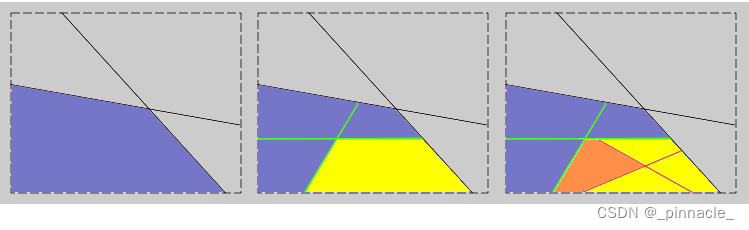
比如我们看上图的两层隐藏层+FC的网络在2维数据上，隐藏层的超平面(第一层红色，第二层灰色)，是完全无矩可寻的，之所以产生这样的空间划分，完全是在数据分布上代价函数最优的结果，不同的初始化参数都会影响超平面的位置。
所以中间层的意义是不明确的，换句话说如果中间层的意义是明确的，那么10层的网络与30层的网络都可以分类同样的数据，那30层网络的后20层的意义是什么？
最小网络结构
我们知道CNN如果没有FC层的话，可以接受大于某个输入大小的任意图像，所以这里有一个最小的网络结构，这个结构其实很简单，就是将最后的输出格点限制为NxCx1x1这时，该格点的感受野为全局感受野，也就是上文中的子结构。这时我们输入大于该感受野的数据，那么将产生NxCxWxH的输出，如上图。
所以我们会发现，绿色格点的任意输出都来自于相同的网络结构与参数，这时如果舍弃FC层，并将任意输出设置为单独的分类，那么这些分类实际是对感受野局部区域的分类，这个也是为什么CNN能用于目标检测的根本原因。
池化层
池化层一般使用比较多的是maxpool和meanpool，本章将解析maxpool的原理，meanpool在本章的代码中基本不会使用所以留待后续分析，maxpool的数学公式可以写成如下形式
m a x p o o l = m a x i ∈ [ 1 , k ] ( y i ) maxpool = max_{i\in[1,k]}(y_i) maxpool=maxi∈[1,k](yi)其中 y i y_i yi可以是 w T x i + b w^\mathsf{T}x_i+b wTxi+b或 R e L U ( w T x i + b ) ReLU(w^\mathsf{T}x_i+b) ReLU(wTxi+b)，需要说明的是 m a x p o o l ∘ R e L U ( x ) maxpool\circ ReLU(x) maxpool∘ReLU(x)与 R e L U ∘ m a x p o o l ( x ) ReLU\circ maxpool(x) ReLU∘maxpool(x)是等价的（meanpool则不等价），为了方便研究我们设置 y i = R e L U ( w T x i + b ) y_i=ReLU(w^\mathsf{T}x_i+b) yi=ReLU(wTxi+b)。我们知道点到分离超平面的距离公式为：
d = ∣ w T x + b ∣ ∥ w ∥ d = \frac{\mid w^Tx+b\mid }{\parallel w\parallel } d=∥w∥∣wTx+b∣可以推出
∣ w T x + b ∣ = d ∥ w ∥ \mid w^Tx+b\mid=d\parallel w\parallel ∣wTx+b∣=d∥w∥因为maxpool是在逐个通道(Channel)运算的，在任意通道中 w , b w,b w,b 是相同的，其范数 ∥ w ∥ \parallel w\parallel ∥w∥也是固定值，所以 max i ∈ [ 1 , k ] ( R e L U ( w T x i + b ) ) \max_{i\in[1,k]}(ReLU(w^\mathsf{T}x_i+b)) maxi∈[1,k](ReLU(wTxi+b))等价于在激活区域中获取离超平面最远的数据点，经过 w , b w,b w,b线性变换后的输出。
反过来说，如果取离超平面的更近的点（即：minpool），因为数据噪声等问题，比如接近超平面边界时有更小的值，数据很容易在边界两侧游离，使得数据变得难分离，所以最大池化层的作用其实就很明显了，对于K个矩阵变换后数据取远离超平面的点，使得数据变得容易分离，也就间接抑制了数据噪声。
总结
本篇文章写的比较粗略，希望读者能理卷积网络的模型逻辑。
参考文献
- On the Number of Linear Regions of Deep Neural Networks
- On the number of response regions of deep feed forward networks with piece- wise linear activations
- On the Expressive Power of Deep Neural Networks
- On the Number of Linear Regions of Convolutional Neural Networks
- Bounding and Counting Linear Regions of Deep Neural Networks
- Multilayer Feedforward Networks Are Universal Approximators
- Facing up to arrangements: face-count formulas for partitions of space by hyperplanes
- An Introduction to Hyperplane Arrangements
- Combinatorial Theory: Hyperplane Arrangements
- Partern Recognition and Machine Learning
- Scikit-Learn Decision Tree
- Neural Networks are Decision Trees
- Unwrapping All ReLU Networks
- Unwrapping The Black Box of Deep ReLU Networks:Interpretability, Diagnostics, and Simplification
- Any Deep ReLU Network is Shallow
- How to Explain Neural Networks: an Approximation Perspective