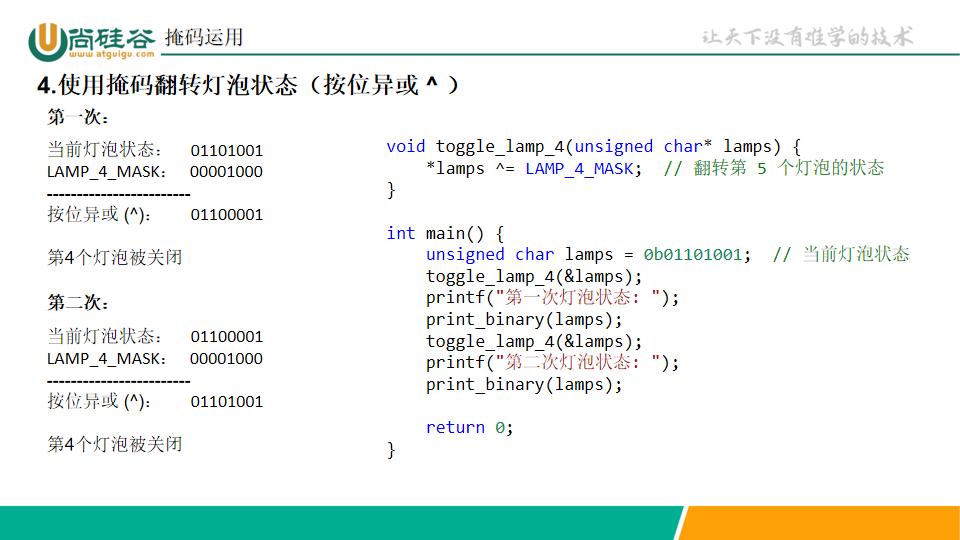
掩码






无人机工程关键代码
cpp
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
{
float norm;
float vx, vy, vz;
float ex, ey, ez;
// 先把这些用得到的值算好
float q0q0 = q0*q0;
float q0q1 = q0*q1;
float q0q2 = q0*q2;
// float q0q3 = q0*q3;
float q1q1 = q1*q1;
// float q1q2 = q1*q2;
float q1q3 = q1*q3;
float q2q2 = q2*q2;
float q2q3 = q2*q3;
float q3q3 = q3*q3;
if(ax*ay*az==0)
return;
norm = sqrt(ax*ax + ay*ay + az*az); //acc数据归一化
ax = ax /norm;
ay = ay / norm;
az = az / norm;
// estimated direction of gravity and flux (v and w) 估计重力方向和流量/变迁
vx = 2*(q1q3 - q0q2); //四元素中xyz的表示
vy = 2*(q0q1 + q2q3);
vz = q0q0 - q1q1 - q2q2 + q3q3 ;
// error is sum of cross product between reference direction of fields and direction measured by sensors
ex = (ay*vz - az*vy) ; //向量外积在相减得到差分就是误差
ey = (az*vx - ax*vz) ;
ez = (ax*vy - ay*vx) ;
exInt = exInt + ex * Ki; //对误差进行积分
eyInt = eyInt + ey * Ki;
ezInt = ezInt + ez * Ki;
// adjusted gyroscope measurements
gx = gx + Kp*ex + exInt; //将误差PI后补偿到陀螺仪,即补偿零点漂移
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt; //这里的gz由于没有观测者进行矫正会产生漂移,表现出来的就是积分自增或自减
// integrate quaternion rate and normalise //四元素的微分方程
q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
q1 = q1 + ( q0*gx + q2*gz - q3*gy)*halfT;
q2 = q2 + ( q0*gy - q1*gz + q3*gx)*halfT;
q3 = q3 + ( q0*gz + q1*gy - q2*gx)*halfT;
// normalise quaternion
norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
q0 = q0 / norm;
q1 = q1 / norm;
q2 = q2 / norm;
q3 = q3 / norm;
Q_ANGLE.Z = GYRO_I.Z;//atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3; // yaw
Q_ANGLE.Y = asin(-2 * q1 * q3 + 2 * q0* q2)* 57.3; // pitch
Q_ANGLE.X = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)* 57.3; // roll
}
b)PID控制部分源码:
void CONTROL(float rol_now, float pit_now, float yaw_now, float rol_tar, float pit_tar, float yaw_tar)
{
u16 moto1 = 0, moto2 = 0, moto3 = 0, moto4 = 0;
vs16 throttle;
float rol = rol_tar + rol_now;
float pit = pit_tar + pit_now;
float yaw = yaw_tar + yaw_now;
throttle = Rc_Get.THROTTLE - 1000;//油门 节流阀
if (throttle < 0) throttle = 0;
PID_ROL.IMAX = throttle / 2;
Get_MxMi(PID_ROL.IMAX, 1000, 0);
PID_PIT.IMAX = PID_ROL.IMAX;
PID_ROL.pout = PID_ROL.P * rol;
PID_PIT.pout = PID_PIT.P * pit;
if (rol_tar * rol_tar < 0.1 && pit_tar * pit_tar < 0.1 && rol_now * rol_now < 30 && pit_now * pit_now < 30 && throttle > 300)
{
PID_ROL.iout += PID_ROL.I * rol;
PID_PIT.iout += PID_PIT.I * pit;
PID_ROL.iout = Get_MxMi(PID_ROL.iout, PID_ROL.IMAX, -PID_ROL.IMAX);
PID_PIT.iout = Get_MxMi(PID_PIT.iout, PID_PIT.IMAX, -PID_PIT.IMAX);
}
else if (throttle < 200)
{
PID_ROL.iout = 0;
PID_PIT.iout = 0;
}
PID_ROL.dout = PID_ROL.D * MPU6050_GYRO_LAST.X;
PID_PIT.dout = PID_PIT.D * MPU6050_GYRO_LAST.Y;
PID_YAW.pout = PID_YAW.P * yaw;
vs16 yaw_d;
if (1480 > Rc_Get.YAW || Rc_Get.YAW > 1520)
{
yaw_d = MPU6050_GYRO_LAST.Z + (Rc_Get.YAW - 1500) * 10;
GYRO_I.Z = 0;
}
else
yaw_d = MPU6050_GYRO_LAST.Z;
PID_YAW.dout = PID_YAW.D * yaw_d;
PID_ROL.OUT = PID_ROL.pout + PID_ROL.iout + PID_ROL.dout;
PID_PIT.OUT = PID_PIT.pout + PID_PIT.iout + PID_PIT.dout;
PID_YAW.OUT = PID_YAW.pout + PID_YAW.iout + PID_YAW.dout;
/*
rol 翻滚
pat 俯仰角
yaw //偏航
*/
if (throttle > 200)
{
#define YAW_ADD (-30)
moto1 = throttle + PID_ROL.OUT - PID_PIT.OUT +YAW_ADD+ PID_YAW.OUT/**/;
moto2 = throttle - PID_ROL.OUT - PID_PIT.OUT -YAW_ADD- PID_YAW.OUT/**/;
moto3 = throttle - PID_ROL.OUT + PID_PIT.OUT +YAW_ADD+ PID_YAW.OUT/**/;
moto4 = throttle + PID_ROL.OUT + PID_PIT.OUT -YAW_ADD- PID_YAW.OUT/**/;
}
else
{
moto1 = 0;
moto2 = 0;
moto3 = 0;
moto4 = 0;
}
if (ARMED) Moto_PwmRflash(moto1, moto2, moto3, moto4);
else Moto_PwmRflash(0, 0, 0, 0);
}四元数
没关系🙂 我再用更生活化的比喻来讲四元数旋转,帮你把公式和几何动作对上号。
🔄 1. 我们要解决的问题
你现在有一个点 P(1,0,0) ,它在 X 轴正方向 上。
你想让它绕 Z 轴 转 90° 。
几何直觉告诉我们:转完应该在 Y 轴正方向,也就是 (0,1,0)。
问题:用四元数怎么计算这个结果?
🧩 2. 四元数就像"旋转的遥控器"
四元数 q 的公式:
q=cos(θ2)+(uxi+uyj+uzk)sin(θ2)q = \cos(\tfrac{\theta}{2}) + (u_x i + u_y j + u_z k)\sin(\tfrac{\theta}{2})
-
θ\theta:旋转角度
-
(ux,uy,uz)(u_x,u_y,u_z):旋转轴方向(必须是单位向量)
👉 可以把它想成一个"遥控器",按下去就能让东西绕某根轴旋转。
🧮 3. 套入具体数字
-
旋转轴是 Z 轴,所以 u=(0,0,1)u=(0,0,1)
-
旋转角度 θ = 90°,所以一半角度 = 45°
于是:
q=cos45°+(0i+0j+1k)sin45°=0.7071+0.7071kq = \cos 45° + (0i + 0j + 1k)\sin 45° = 0.7071 + 0.7071k
(就是一个有"实部"和"虚部"的数)
🟦 4. 点也要变成四元数
点 P(1,0,0),写成四元数:
p=0+1i+0j+0k=ip = 0 + 1i + 0j + 0k = i
(注意:点用"纯虚四元数"表示)
⚙️ 5. 旋转公式
旋转用这个公式:
p′=q p q∗p' = q \, p \, q^*
其中 q∗q^* 是 q 的"共轭"(把虚部取反)。
这里:
q=0.7071+0.7071k,q∗=0.7071−0.7071kq = 0.7071 + 0.7071k, \quad q^* = 0.7071 - 0.7071k
✍️ 6. 动手算一下(关键步骤)
-
先算 q * p:
(0.7071+0.7071k)(i)=0.7071i+0.7071(ki)(0.7071 + 0.7071k)(i) = 0.7071i + 0.7071(ki)
记住规则:
i2=j2=k2=−1,ij=k,jk=i,ki=ji^2 = j^2 = k^2 = -1, \quad ij = k, \quad jk = i, \quad ki = j所以 ki=jki = j,得到:
q⋅p=0.7071i+0.7071jq \cdot p = 0.7071i + 0.7071j -
再乘上 q*:
(0.7071i+0.7071j)(0.7071−0.7071k)(0.7071i + 0.7071j)(0.7071 - 0.7071k)
经过展开化简,结果是:
p′=jp' = j
✅ 7. 结果
p′=j⇒(0,1,0)p' = j \quad \Rightarrow \quad (0,1,0)
这和几何直觉完全一致:
点 (1,0,0) 绕 Z 轴转 90° → 变成 (0,1,0)。
🎯 最终一句话总结
四元数就是一个"旋转遥控器",
公式 p′=qpq∗p' = qpq^* 只是数学的写法,
算出来的结果,和你脑子里画的旋转效果是一模一样的。
要不要我帮你做一个动画演示图(小球在 XY 平面绕 Z 轴转 90°,同时写出 q、p、p' 的对应关系)?这样你一眼就能对上公式和几何动作。
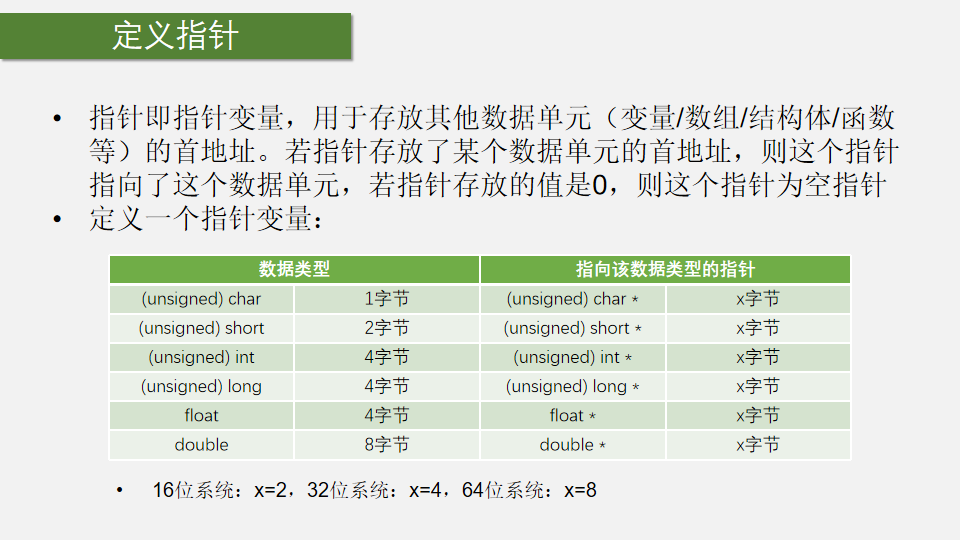
指针