1.开头
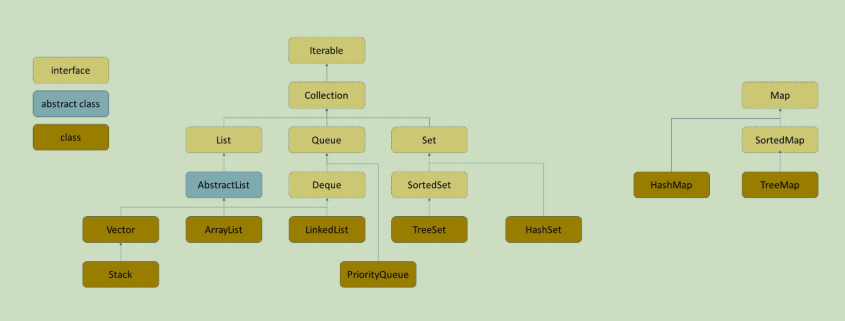
在此之前,我们要先来了解 TreeMap 和 TreeSet 的使用;从上图我们可以看出,TreeMap 和 HashMap 都属于Map,而 Map 比较特殊,它不属于 Collection,而是自己作为父类。
TreeSet 和 HashMap 的结构与 Map 类似,TreeSet 属于 SortedSet,SortedSet 属于 Set;而 HashSet 直接属于 Set 。
由于 TreeMap 和 TreeSet 的使用是基于二叉搜索树来完成的,所以我们要先来进行二叉搜索树的学习。
2.二叉搜索树
二叉搜索树(Binary Search Tree, BST)是一种特殊的二叉树,满足以下性质:
-
对于树中的每个节点,其左子树中的所有节点的值均小于该节点的值。
-
其右子树 中的所有节点的值均大于该节点的值。
-
左右子树也分别为二叉搜索树。
-
节点中不能有相同的值。
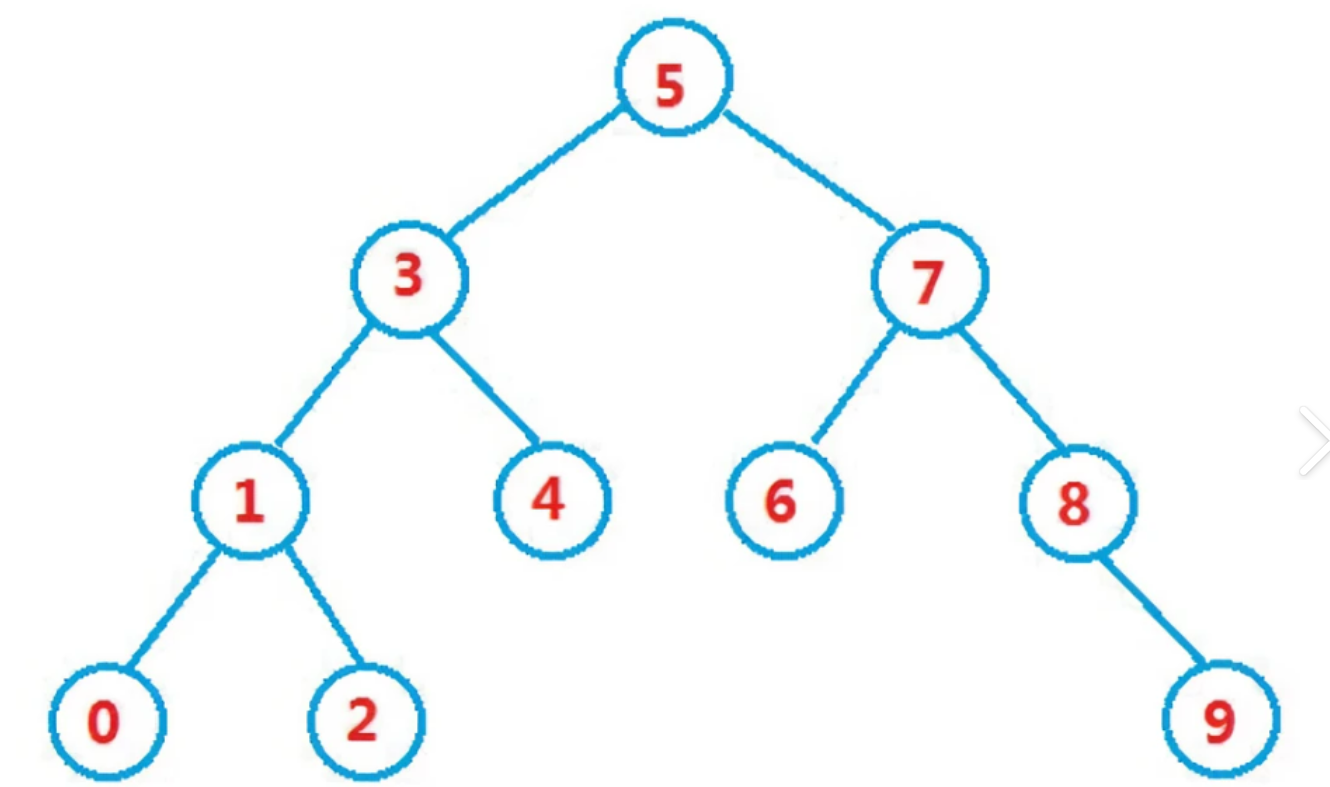
关于二叉搜索树,它也与二叉树一样,也有增删查改的操作,现在我们一个个来看看。
2.1 查找
2.1.1 基本思路
既然是查找元素,那么可能就会有以下三种情况,大家可以先猜一猜:
-
树为空时的情况;当树为空的时候,由于二叉树的节点是引用类型,所以我们要 return null。
-
树不为空 的情况;树不为空的时候,那在查找的时候就会出现要查找的值比当前的值要小的时候和比当前节点值要大的时候,这里我们就要分情况讨论,也很简单。首先定义一个指针 cur ,从根节点 开始走,比当比当前节点值要小的时候,让 cur 向左走;反之则向右走。直到能够找到元素或者是全部遍历完了还没找到的情况,那就要看下一步了。
-
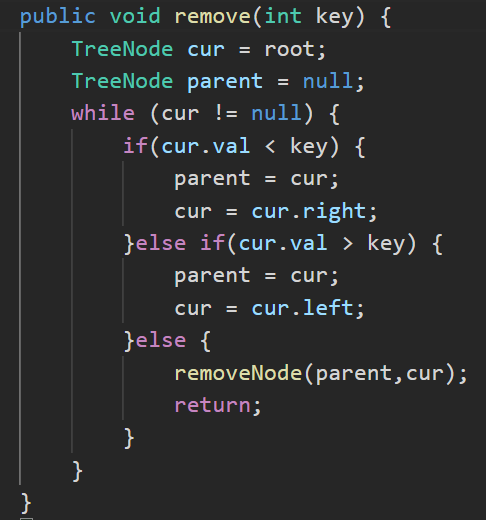
找不到元素的情况。我们直接 return null 即可。下图为代码实现:
2.2.2 代码实现

查找的时间复杂度:最好情况:O(logN),以2为底。
最坏情况:O(N)。
2.2 插入
2.2.1 基本思路
插入元素,也有可能会出现以下情况,大家同样先猜一猜,这一步也是为了锻炼你们的思考能力,自己尝试思考还是非常重要的。
- 该树没有元素,即为空树;这时我们直接插入即可。
2.该树有元素,那我们就要先查找,查找到合适的位置时我们再进行插入;那话说回来,我们刚刚是不是已经写过查找的代码了?所以这一步咱们可以直接沿用上面写好的代码。然后插入时我们要注意,如果你和插入一样只用一个指针去遍历的话,那到最后你也只是找到要插入的节点,但不能进行插入,因为那个节点是空指针 ,你直接插入的话会引发空指针异常!!!这一点需要注意。那么该如何去解决呢?也很简单,再申请一个变量 parent ,这个变量的指向每次都指向上次的 cur 的指向,最后执行插入的时候,我们直接让 parent 的左或右是要插入的 node 就行了。
大家可以IDEA中自己尝试一下,下图是代码实现:
2.2.2 代码实现

2.3 删除
2.3.1 基本思路
这个删除的操作相比前两个操作来说会难一些,因为有一种情况会比较难处理,我们先来一个个看看各种情况。
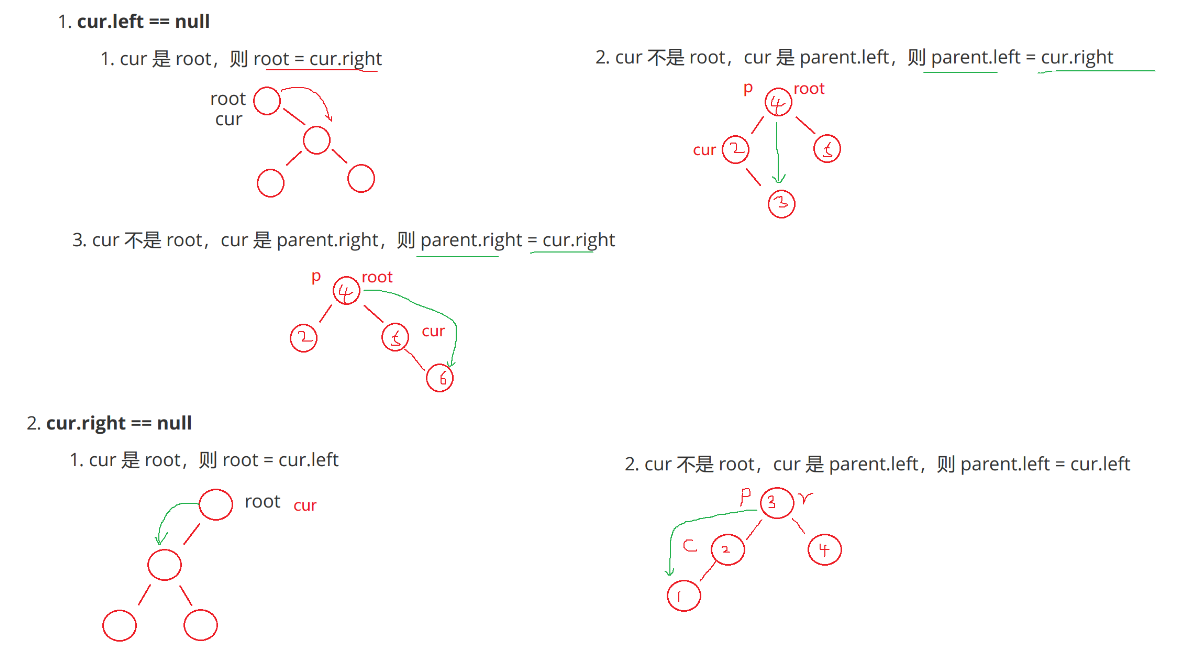
1. cur.left == null
(1) cur 是 root,则 root = cur.right
(2) cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
(3) cur 不是 root,cur 是 parent.right,则 parent.right = cur.right
2. cur.right == null
(1) cur 是 root,则 root = cur.left
(2)cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
(3) cur 不是 root,cur 是 parent.right,则 parent.right = cur.left
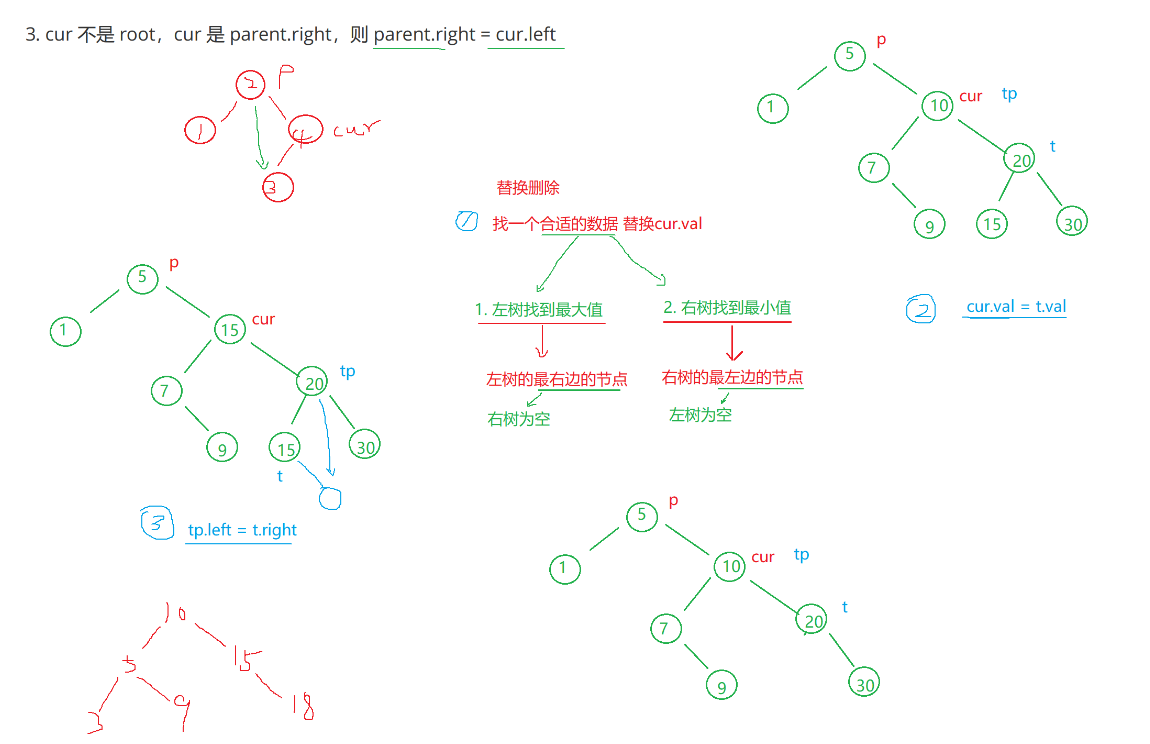
3. cur.left != null && cur.right != null
需要使用替换删除法进行删除:在它的左子树找到最大值节点或在它的右子树中找到,用它的值填补到被删除节点中,再来处理该结点的删除问题。
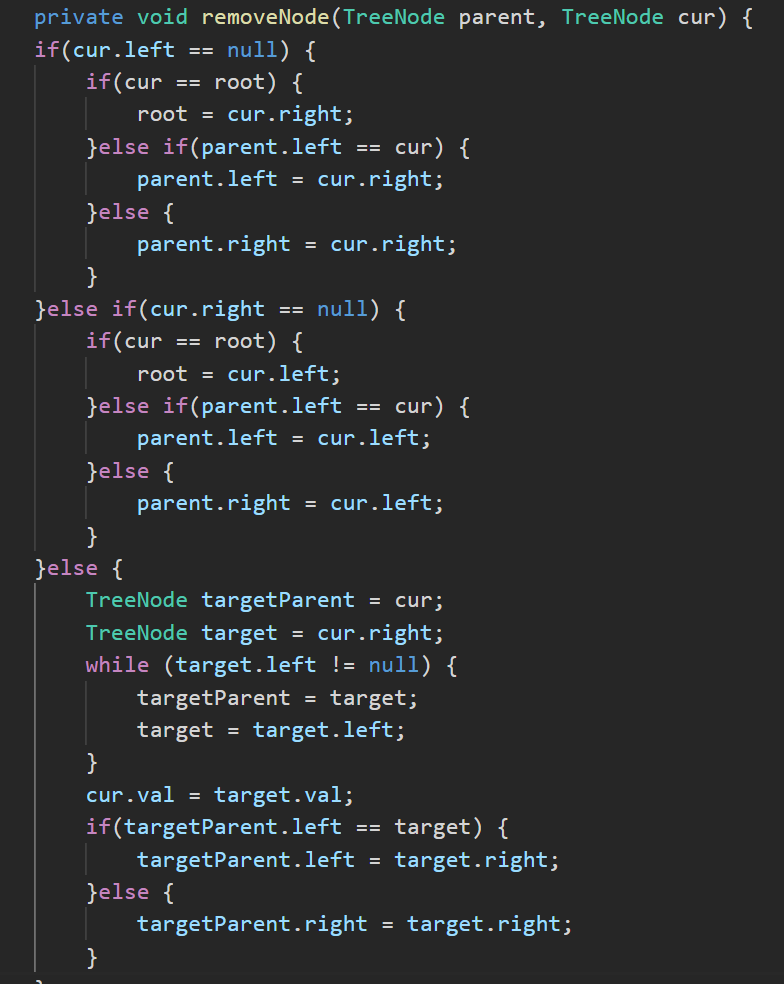
2.3.2 代码实现
在删除之前,同样我们要查找被删除元素的元素。此时,查找的代码同样可以再次被运用,这一部分直接摘下来即可。由于替换删除法是需要"用合适的值填补到被删除节点中",那么其实也就是插入,所以这里插入的代码我们也可以摘下来。到头来,实际上我们要完成的就是删除部分的代码。
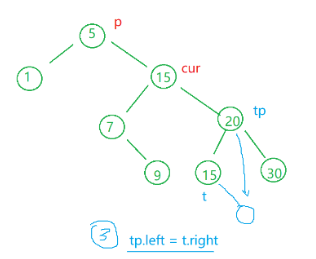
删除部分:这里只讲左树与右树情况下的查找替换法。(这里以右树的最小值为例)
与替换法类似,这里我们定义 targetParent 和 target 。(和 parent 和 cur 类似)既然我们是以右树的最小值为例,那么右树的最小值一定在它的最左边的叶子结点,所以我们要让刚刚定义的指针一直往左走即可(这一步是要写成循环的)。走完之后说明肯定是找到了,那我们就令准备被删除的值等于该节点的值。
最后,我们需要调整一下这个二叉搜索树,因为它不能存在相同的值。有一种情况可能会出现:假如 target 的左边没有节点而右边有节点,那我们就需要 targetParent.left = target.right;反之我们就 targetParent.right = target.right;
3. 二叉搜索树总结

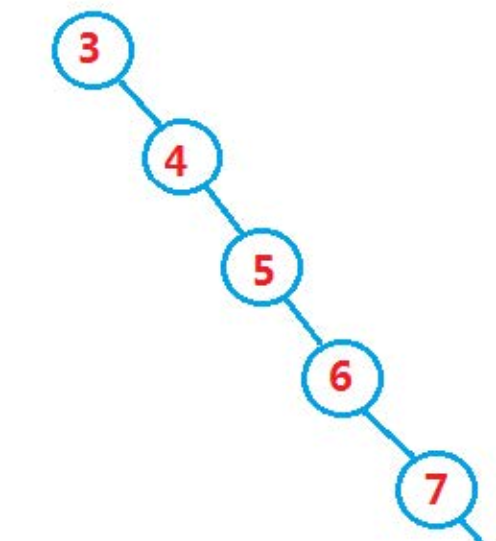
单支树
如果退化成单支树,二叉搜索树的性能就失去了。必须要是二叉平衡树,才能达到logN,那我们该如何改进,才能避免单支树拖慢时间复杂度呢?
答:这里我们就要去运用 Map 和 Set 去解决了。这部分下篇文章我们再去讲。
4. 习题
一个学习的过程中少不了习题的巩固,让我们来做一些习题吧。

答:D;C选项从概念中可以得出以下性质:
-
二叉搜索树中最左侧节点一定是最小的,最右侧节点一定是最大的;
-
对二叉搜索树进行中序遍历,可以得到一个有序的序列。
而D选项,在单支树情况下时间复杂度会达到O(N),C选项错误。

答:B;二叉搜索树有个特性:中序遍历的结果是有序的。

答:A;由概念可知。
下一个文章我们就会讲到 HashSet 和 HashMap ,这一部分对于许多算法题都会用到,十分重要。
那么,本篇文章到此结束!
本篇文章的截图,部分摘自于比特科技 。希望能对你有帮助。