分治算法-快排

算法原理

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，从后边开始找到比基准小的停下来，从前面开始找到比基准大的停下来直至两个相遇，相遇的即为新基准，找到基准后再分两边找，类似二叉树

时间复杂度：当给定1，2,3,4......有序情况下0（n^2）

当每次都能均匀分开时0(logN)

空间复杂度：最坏单分支树0（N）最好情况：0（logN）完全二叉树

稳定性：不稳定的排序

挖坑法（做题优先考虑的思想）：先把left（0）拿出，0坐标空出即为坑，从后边找比基准小的直接填坑，再从前边找比基准大的挖坑

前后指针法：两个指针prev和cur

prev=legft，cur=left+1

一前一后走，找到比基准小的进行交换

优化思路：减少他的递归次数

1.三数取中法（left，right，mid找到这三个数据中）

2.直接插入法（针对一定范围）二叉树越深，递归次数越多，可以在最后几层直接插入排序（因为数据少且趋于有序）

题目解析

1.颜色分类

https://leetcode.cn/problems/sort-colors/description/

题目描述

给定一个包含红色白色和蓝色,共n个元素的数组nums,原地对他们进行排序,使得相同颜色的元素相邻,并且按照红色,白色,蓝色顺序进行排列,我们使用0,1,2分别表示红色,白色和蓝色(在不使用内置sort的情况下解决这个问题)

算法原理

上图就是我们最终要使数组达到的状态

利用三指针来解决问题,一个指针i来遍历数组,left用来记录左边界,right用来记录右边界

0,left\]的值都为0,\[left+1,i-1\]值为1,\[i,right-1\]未知(仍然需要遍历),\[right,n-1\]的值为2 遇到0,要交换nums\[++left\]和nums\[i++

遇到1,i++

遇到2,交换nums[i],nums[--right](为什么此处i不用加加?因为此处交换过来的元素是谁并不知道)

以一个具体的例子来说明:

代码实现

java 复制代码

class Solution {
    public void sortColors(int[] nums) {
        int left=-1,right=nums.length;
        int i=0;
        while(i<right){
            if(nums[i]==0){
                swap(nums,i++,++left);
            }else if(nums[i]==1){
                i++;
            }else{
                swap(nums,i,--right);
            }
        }
    }
    public void swap(int[]nums,int i,int j){
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }
}

2.快速排序

https://leetcode.cn/problems/sort-an-array/

题目描述

给定一个整数数组nums,请将该数组升序排列

算法原理

用数组分三块的思想来实现快速排序

快速排序,选择基准元素,然后以基准元素为主,先排左边,再排右边

然后再定义两个指针,将左右的元素比较按照大小填入到临时数组中(因为我们会经常使用这个数组,所以我们可以将其设为全局变量),然后再将这个临时数组对应的填到原数组中

(这是个不断递归的过程)

当left>=right返回此时已经排完序了

优化用随机的方式选择基准

代码实现

java 复制代码

    int[] tmp;
    public int[] sortArray(int[] nums) {
        tmp=new int[nums.length];
        mergeSort(nums,0,nums.length-1);
        return nums;
    }
    public void mergeSort(int[]nums,int left,int right){
        if(left>=right){
            return;
        }
        int mid=(left+right)/2;
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid&&cur2<=right){
            tmp[i++]=nums[cur1]<=nums[cur2]?nums[cur1++]:nums[cur2++];
        }
        while(cur1<=mid){
            tmp[i++]=nums[cur1++];
        }
        while(cur2<=right){
            tmp[i++]=nums[cur2++];
        }
        for(int j=left;j<=right;j++){
            nums[j]=tmp[j-left];
        }
    }

3.数组中的第k个最大元素

https://leetcode.cn/problems/kth-largest-element-in-an-array/description/

题目描述

给定整数数组nums和整数k,请返回数组中第k个最大的元素

算法原理

数组分三块+随机选择基准元素

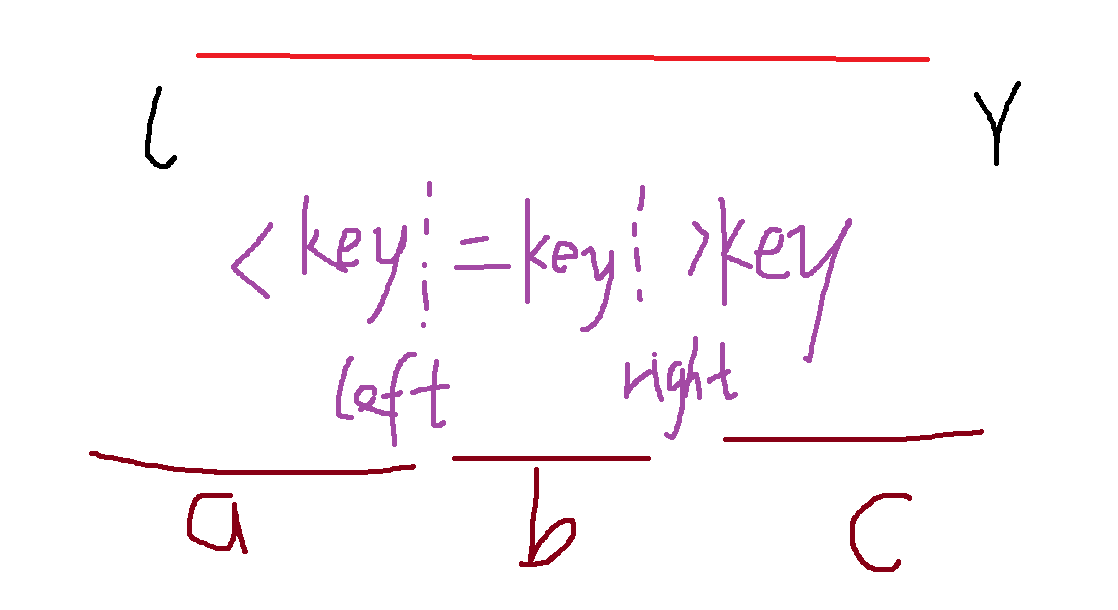
当c>=k时,那么我们可以确定最终元素在[right,r]区间内,只需在[right,r]内寻找即可

当c+b>=k时,返回key

当上述条件都不成立的时候,在[l,left]内寻找k-b-c大元素

代码实现

java 复制代码

    public int findKthLargest(int[] nums, int k) {
        int ret=findKey(nums,0,nums.length-1,k);
        return ret;
    }
    public int findKey(int[]nums,int l,int r,int k){
        if(l==r){
            return nums[l];
        }
        int key=nums[new Random().nextInt(r-l+1)+l];
        int left=l-1,right=r+1,i=l;
        while(i<right){
            if(nums[i]<key){
                swap(nums,++left,i++);
            }else if(nums[i]>key){
                swap(nums,--right,i);
            }else{
                i++;
            }
        }
        int c=r-right+1,b=right-left-1;
        if(c>=k){
            return findKey(nums,right,r,k);
        }else if(b+c>=k){
            return key;
        }else{
            return findKey(nums,l,left,k-b-c);
        }
    }
    public void swap(int[] nums,int i,int j){
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }

4.最小k个数

https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/description/

题目描述

输入整数数组arr,找出其中最小的k个数

算法原理

解法一:排序logN

解法二:堆(大根堆) NlogK

解法三:快速选择 O(N)(这里我们着重讲解这一方法)

随机选择+数组分三块

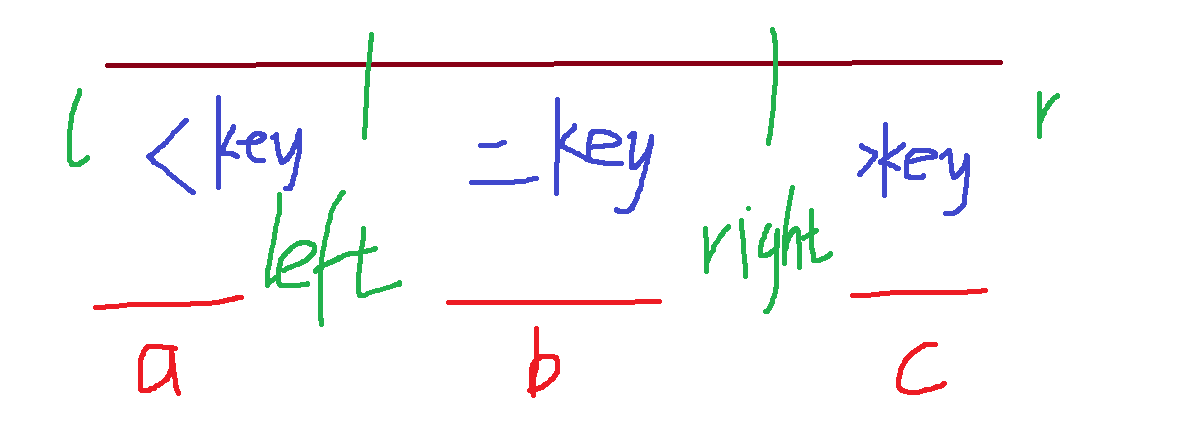
当a>k,在[l,left]内寻找最小k

当a+b>=k,返回

当上述都不成立,[right-r]内寻找k-b-a

代码实现

java 复制代码

    public int[] inventoryManagement(int[] s, int k) {
        sqort(s,0,s.length-1,k);
        int[] ret=new int[k];
        for(int i=0;i<k;i++){
            ret[i]=s[i];
        }
        return ret;
    }
    public void sqort(int[] nums,int l,int r,int k){
        int key=nums[new Random().nextInt(r-l+1)+l];
        int left=l-1,right=r+1,i=l;
        while(i<right){
            if(nums[i]<key){
                swap(nums,++left,i++);
            }else if(nums[i]>key){
                swap(nums,--right,i);
            }else{
                i++;
            }
        }
        int a=left-l+1,b=right-left-1;
        if(a>k){
         sqort(nums,l,left,k);
        }else if(a+b>=k){
            return ;
        }else{
            sqort(nums,right,r,k-a-b);
        }
    }
    public void swap(int[] nums,int i,int j){
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }