- 理论:根据气温预测是否出门
-
- 逻辑回归的假设函数
-
- [给 Sigmoid 函数增加缩放参数](#给 Sigmoid 函数增加缩放参数)
- [给 Sigmoid 函数增加平移参数](#给 Sigmoid 函数增加平移参数)
- [一元逻辑回归模型的假设函数(Sigmoid 作为激活函数)](#一元逻辑回归模型的假设函数(Sigmoid 作为激活函数))
- 逻辑回归的损失函数
- 多元逻辑回归
- 逻辑回归的决策边界只能是直线吗?
- 逻辑回归只能解决二分类问题吗?
监督学习中,除了回归问题,另一类应用非常广的算法就是 分类算法。
比如根据用户的特征判断用户会不会违约;根据一朵花花瓣和花萼的长度宽度,预测花的种类等;根据用户特征,判断用户会不会点击这个广告。
千万不要被逻辑回归里的"回归"误导,逻辑回归是一个分类问题的算法 。这也是机器学习 历史遗留 的用词不规范的地方。
理论:根据气温预测是否出门
从一个例子开始,假设统计了小明每天是否出门与当天气温的数据。0 代表不出门,1 代表出门。
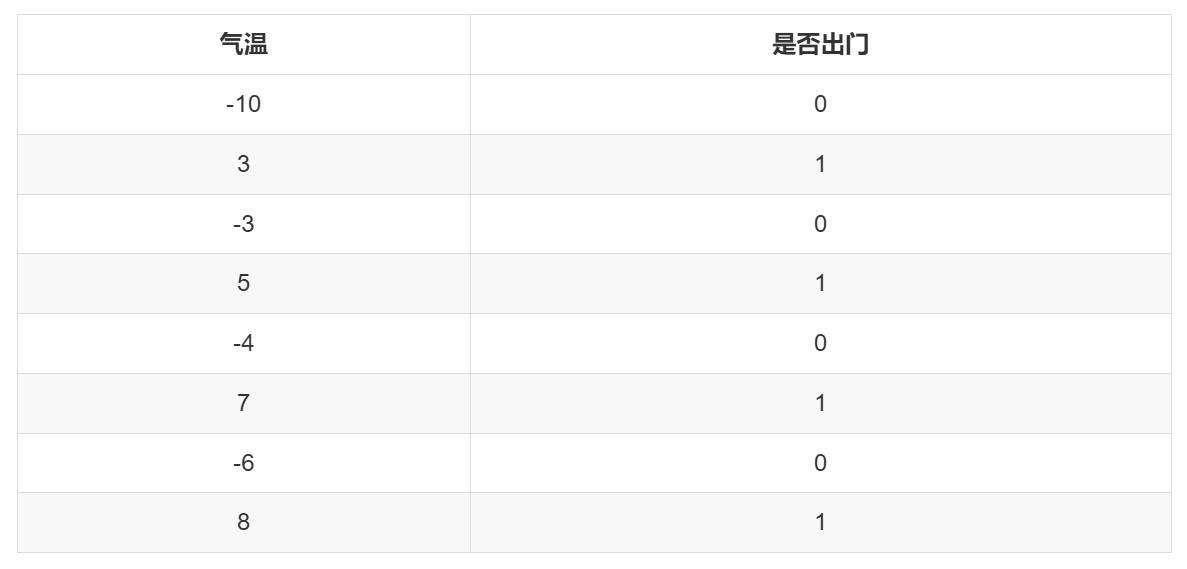
将上边的数据绘制散点图如下:
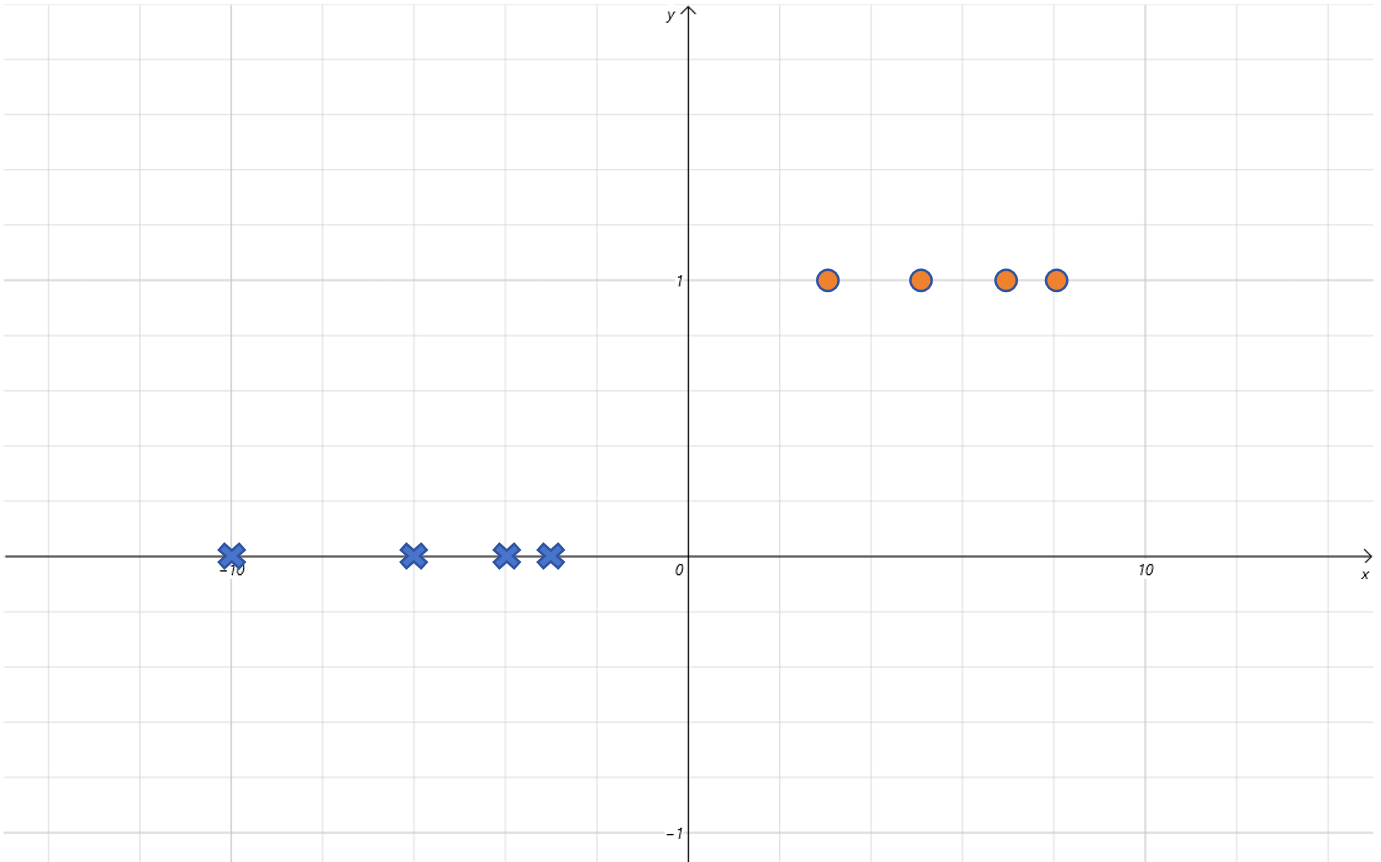
我们需要训练一个模型,根据气温来预测小明是否出门。线性回归模型用在这里不合适,因为这里 Label 的取值只有两个,非 0 即 1,是个分类问题 。如果用简单的一元一次线性方程,它预测的 Label 会一直变化,突破 [0,1] 的范围,所以是不能拟合这个图像的。
逻辑回归的假设函数
既然 线性函数不适合,那人们就寻找其他函数 。最后找到这么一个函数,Sigmoid 函数:
sigmoid ( x ) = 1 1 + e − x \text{sigmoid}(x) = \frac{1}{1 + e^{-x}} sigmoid(x)=1+e−x1
将这个函数的曲线绘制出来,如下:
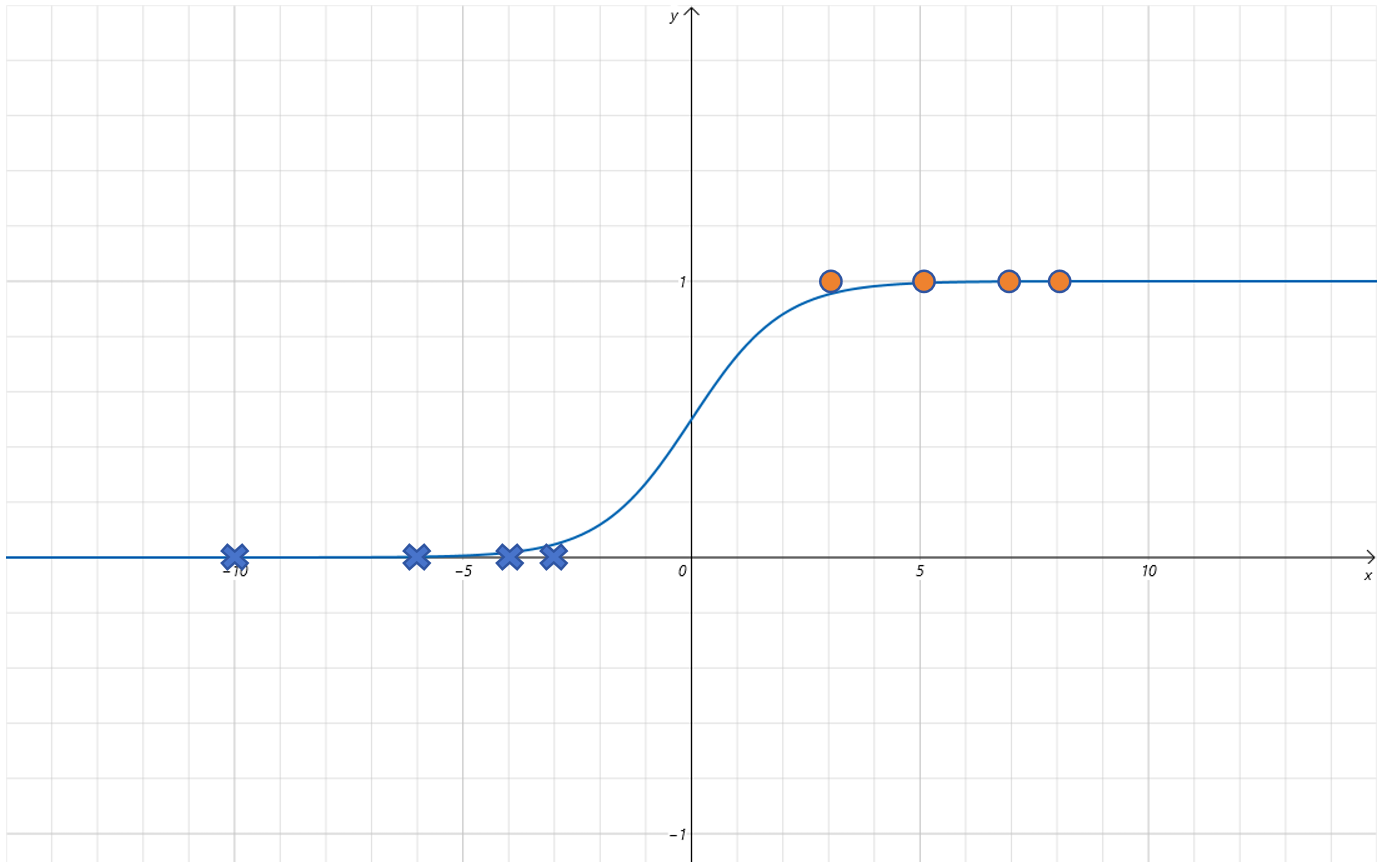
可以看到 Sigmoid 函数有很好的特性,它的 输出值区间为 [0,1] ,而且 只有 x 取值在 0 附近时,函数值有明显的变化,其他区间都很非常接近 0 或者 1。
可以把 Sigmoid 的函数值作为在气温为 x x x 下,对小明出门概率的预测。比如当气温为 − 10 -10 −10 时,预测小明出门的概率接近 0,气温为 10 10 10,预测小明出门的概率接近 1。在气温为 − 1 -1 −1 时,预测小明出门概率大概为 0.3。
所以,用 Sigmoid 函数可以很好的作为二分类问题的假设函数 。线性回归的假设函数为线性方程,它假设 Feature 和 Label 之间满足线性关系。而 二分类问题 的假设函数为 Sigmoid ,它假设输入 x x x 和输出 y y y 之间满足 Sigmoid 函数的映射关系。
给 Sigmoid 函数增加缩放参数
但是只用 Sigmoid 函数作为假设函数,里边完全没有可以训练的参数。Sigmoid 函数的图像完全是固定的,但是不是所有的二分类问题都可以映射到标准的 Sigmoid 函数上。
可以给 Sigmoid 函数里的 x x x 前边增加一个参数 w w w,
sigmoid ( w x ) = 1 1 + e − w x \text{sigmoid}(wx) = \frac{1}{1+e^{-wx}} sigmoid(wx)=1+e−wx1
尝试调整 w w w 这个参数。
-
当设置 w = 0.5 w=0.5 w=0.5 时,函数曲线变为:
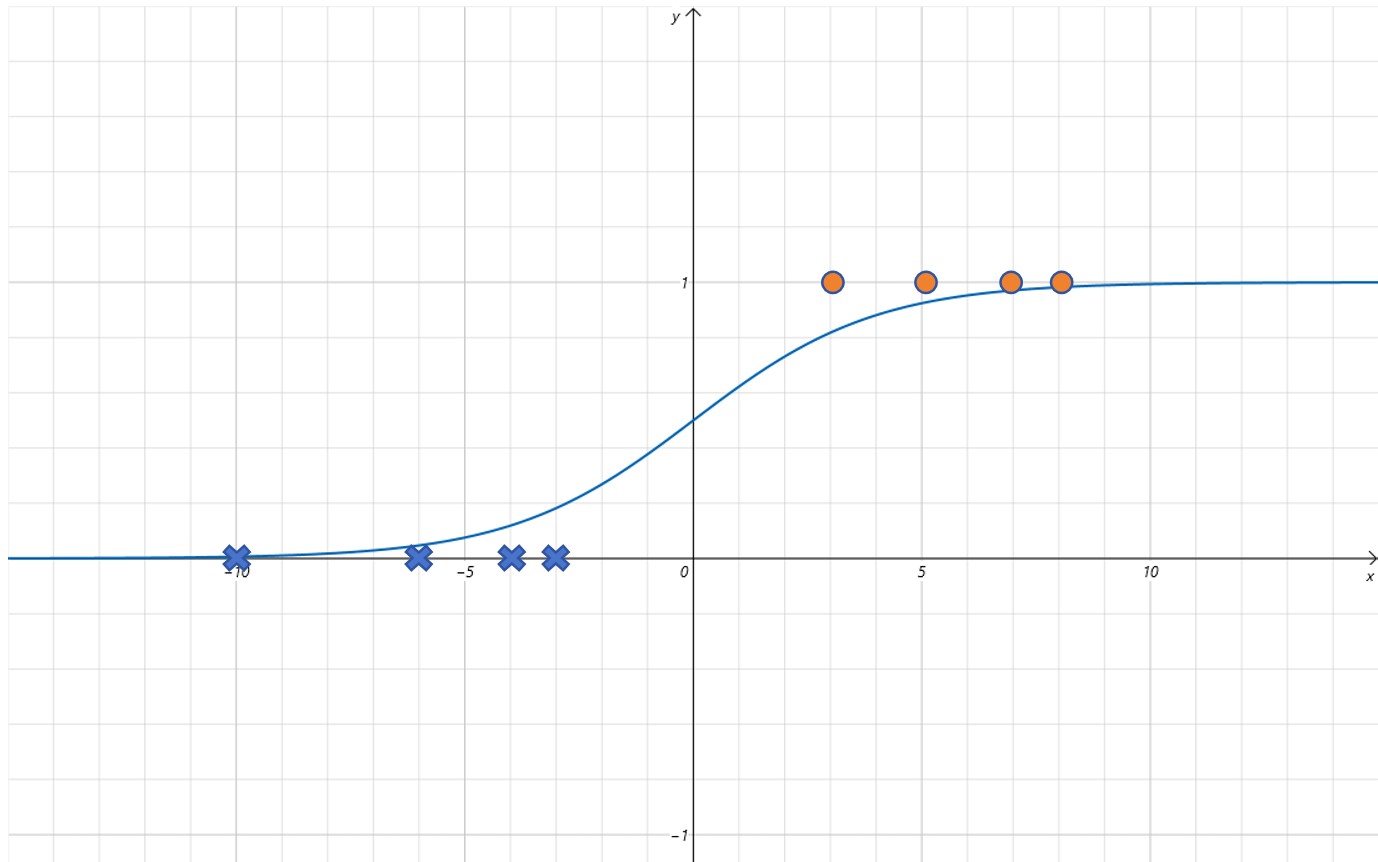
可以发现 函数曲线沿着 x x x 轴方向拉伸了。
-
当设置 w = 2 w=2 w=2 时,函数曲线变为:
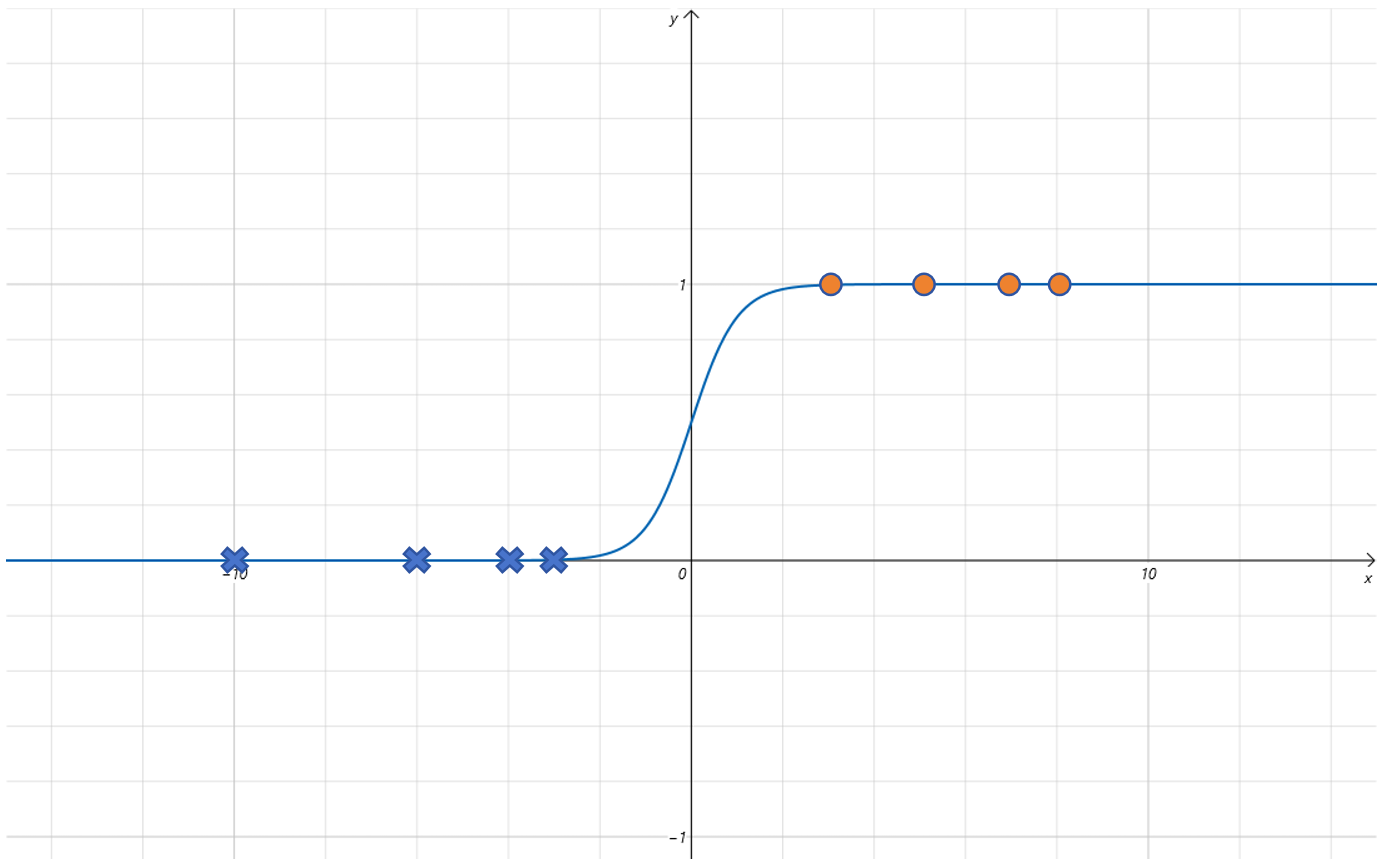
可以发现 函数曲线沿着 x x x 轴方向压缩了。
所以 增加一个可以训练调整的参数 w w w ,就可以 让模型更加拟合数据。
下面这些数据点是左高右低,也就是 x x x 取值较小的部分,Label 值为 1, x x x 取值较大的部分,Label 值为 0。这和 Sigmoid 左低右高刚好的相反的。
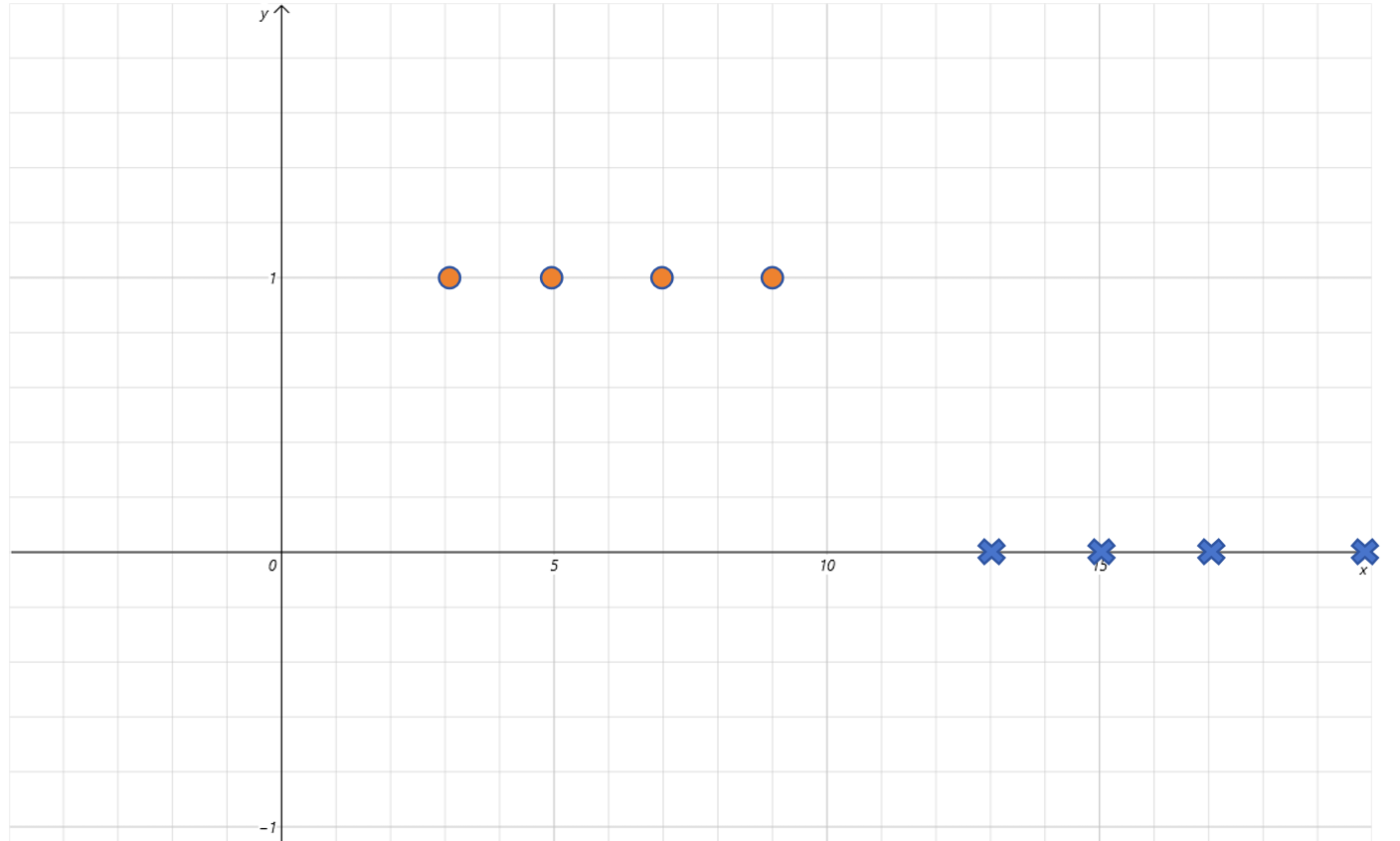
不过没关系,我们已经给 Sigmoid 函数增加了参数 w w w。可以让 w w w 为负值来解决这个问题。比如让 w = − 2 w=-2 w=−2,对应的函数曲线如下:
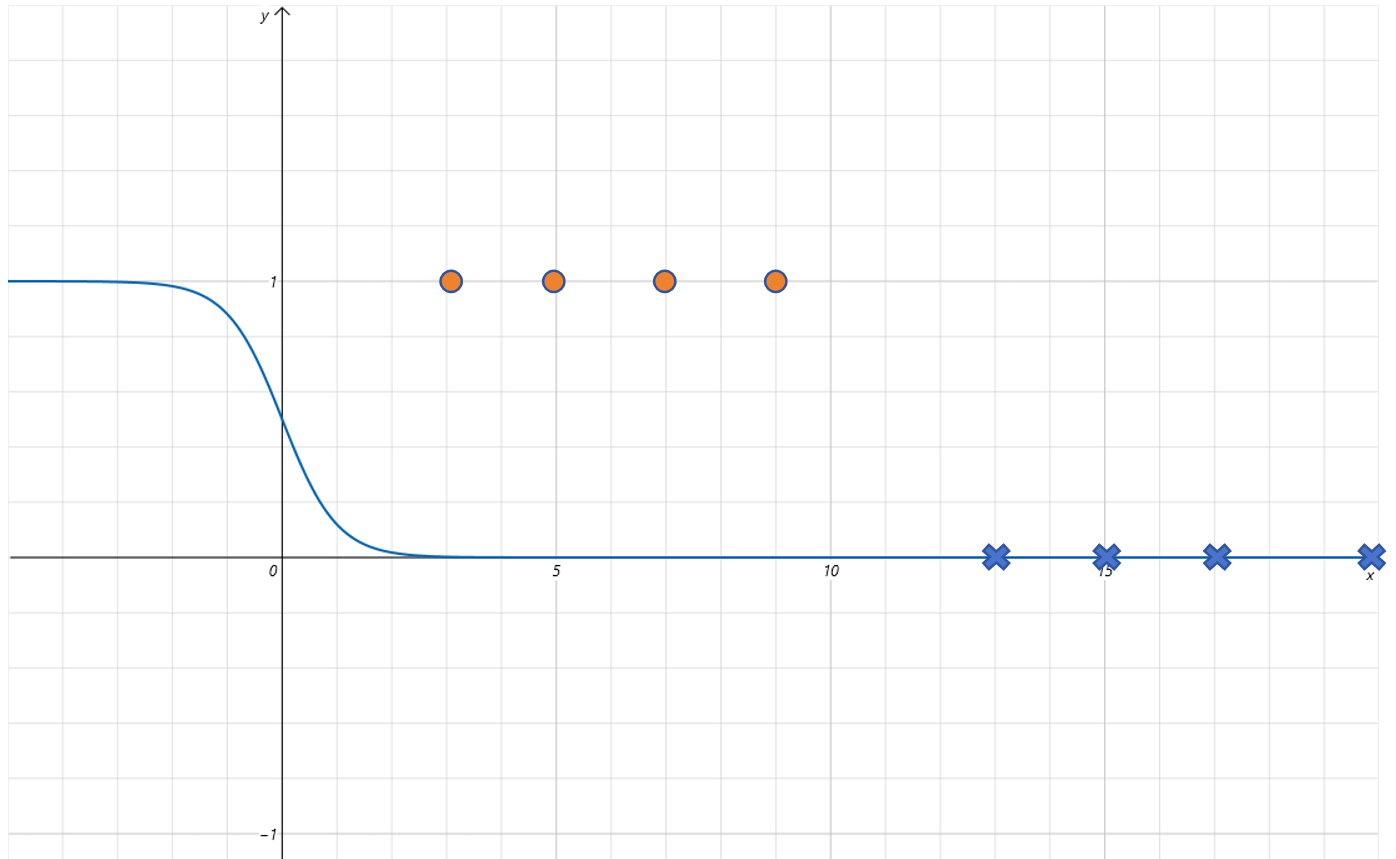
给 Sigmoid 函数增加平移参数
根据上边图像看,还需要对 Sigmoid 函数进行平移才可以拟合这些点,那就给 Sigmoid 函数再增加一个参数 b b b。
当设置 w = − 2 , b = 22 w=-2,b=22 w=−2,b=22 时,函数图像为:
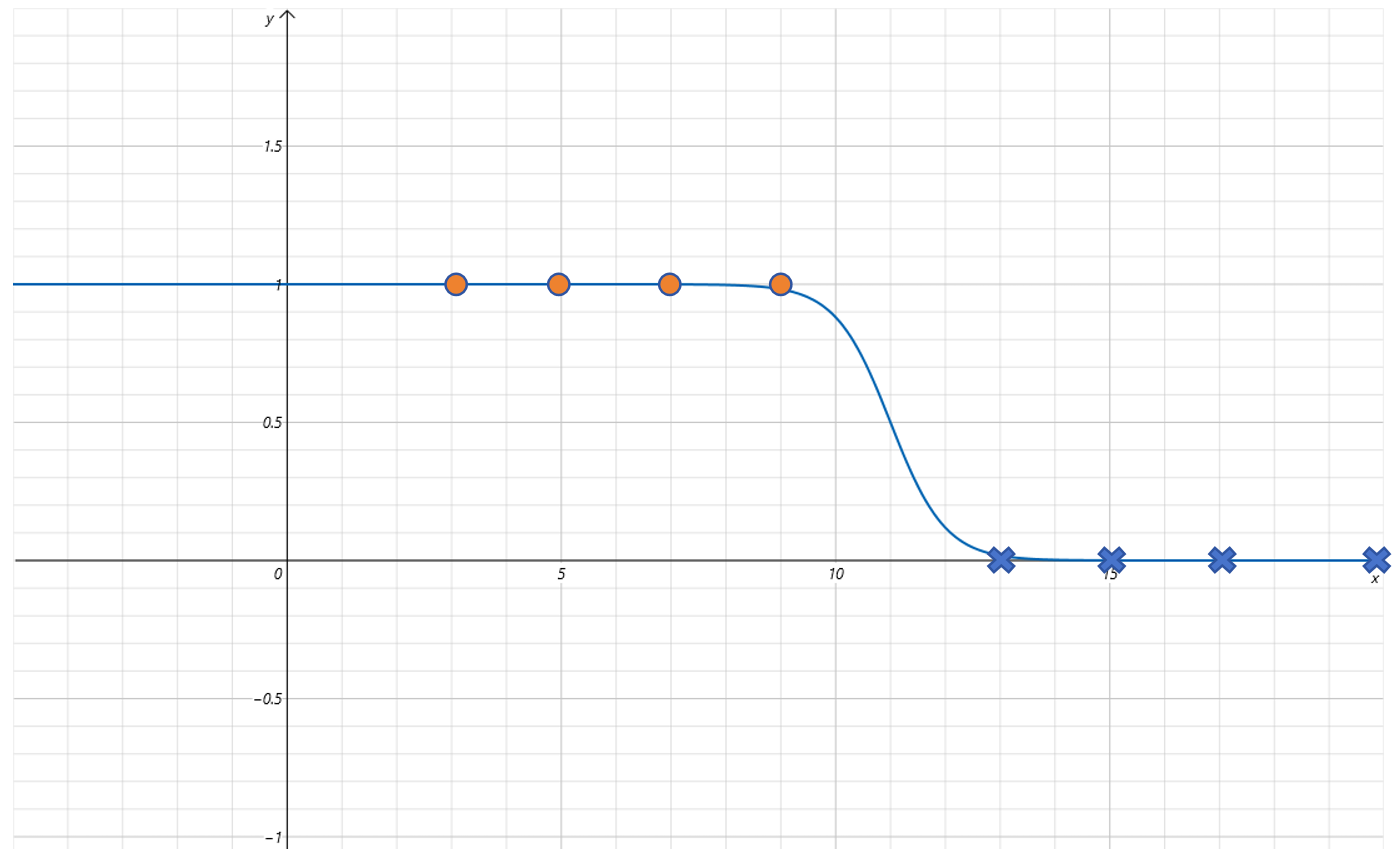
可以发现对 Sigmoid 函数增加 w w w 和 b b b 参数就可以很好的拟合这些点了。通过训练模型,让模型自己找到合适的 w w w 和 b b b 的值。
一元逻辑回归模型的假设函数(Sigmoid 作为激活函数)
一元逻辑回归模型的假设函数为:
LogisticRegression ( x ) = Sigmoid ( w x + b ) = 1 1 + e − ( w x + b ) \text{LogisticRegression}(x) = \text{Sigmoid}(wx+b) = \frac{1}{1 + e^{-(wx+b)}} LogisticRegression(x)=Sigmoid(wx+b)=1+e−(wx+b)1
其中的 w w w 和 b b b 参数会对标准的 Sigmoid 函数曲线进行平移,翻转,缩放等 。最终将输出映射到 [0,1]。
对 Sigmoid 函数的输入 x x x,增加了 w w w 和 b b b 参数。实际上就是 对 x x x 应用了一个线性回归,然后再进行 Sigmoid 变化。 所以可以理解为 一元逻辑回归就是在线性回归的基础上,增加了一个 Sigmoid 函数。
这个 Sigmoid 函数叫做 激活函数 。在深度学习里,输入首先经过一个线性变化,然后经过一个非线性的函数,比如这里的 Sigmoid 函数。这个 非线性的函数 就叫做激活函数。激活函数的作用就是在 线性函数的基础上增加了非线性。
Sigmoid 函数在 输入小于 0 0 0 的时候,对输出产生抑制作用,输出接近于 0 0 0 ;当 输入大于 0 0 0 时,产生激活作用,输出快速接近 1 1 1。
逻辑回归的损失函数
训练一个模型 ,就需要定义 损失函数 ,然后利用梯度下降算法,让损失越来越小。最终得到 让损失最小的模型参数。
预测 就是利用训练好的模型参数和新采集的 Feature,代入假设函数,预测一个输出。
试一试逻辑回归是否也可以利用 MSE 作为损失函数。
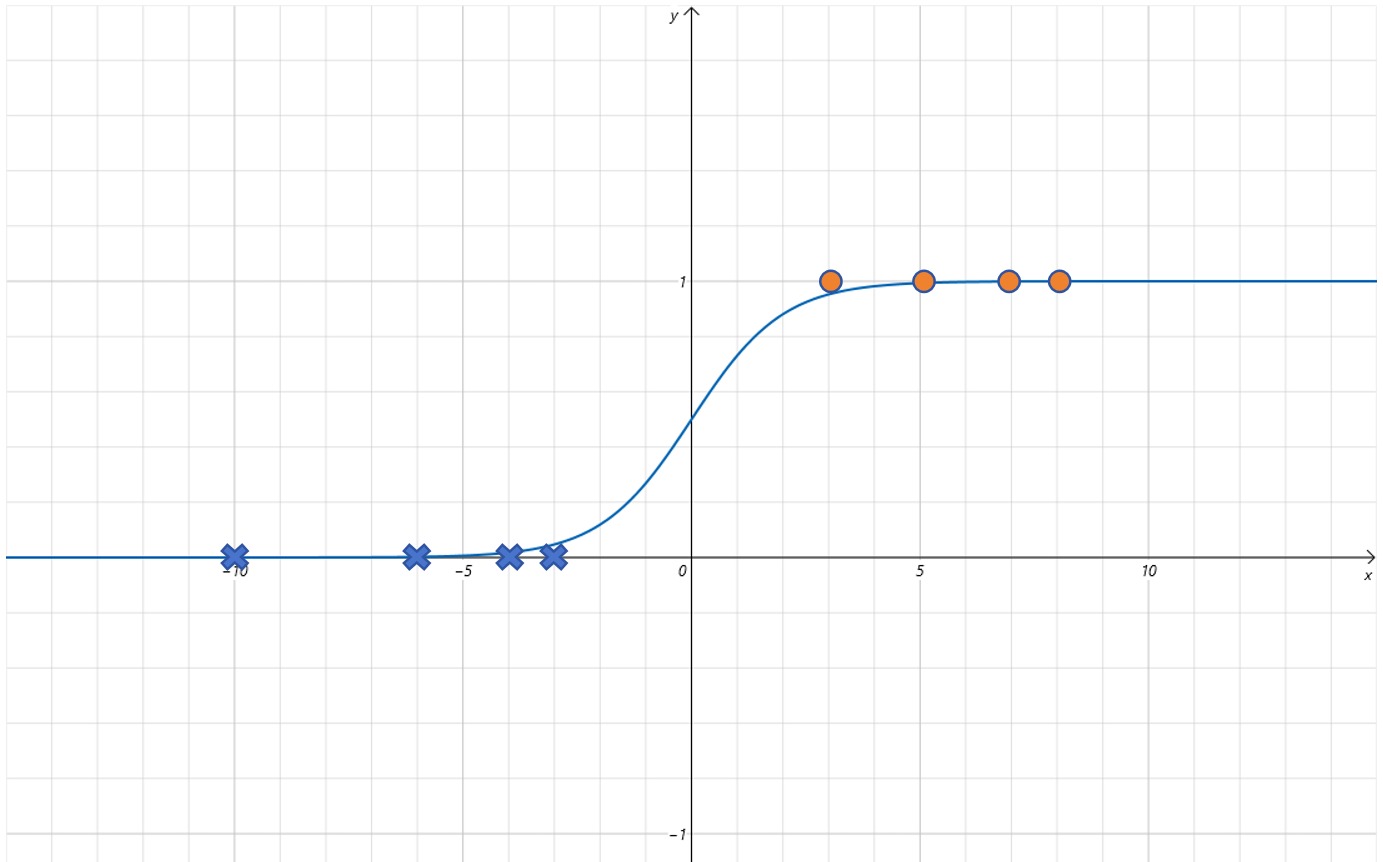
对于上边的以气温数据预测小明是否出门的二分类例子,代入实际的 feature 和 label 值,构建 MSE loss 函数,最终的 MSE loss 函数表达式是由参数 w w w 和 b b b 构成的。接下来 优化的目标就是寻找让 MSE loss 最小的 w w w 和 b b b 的值。
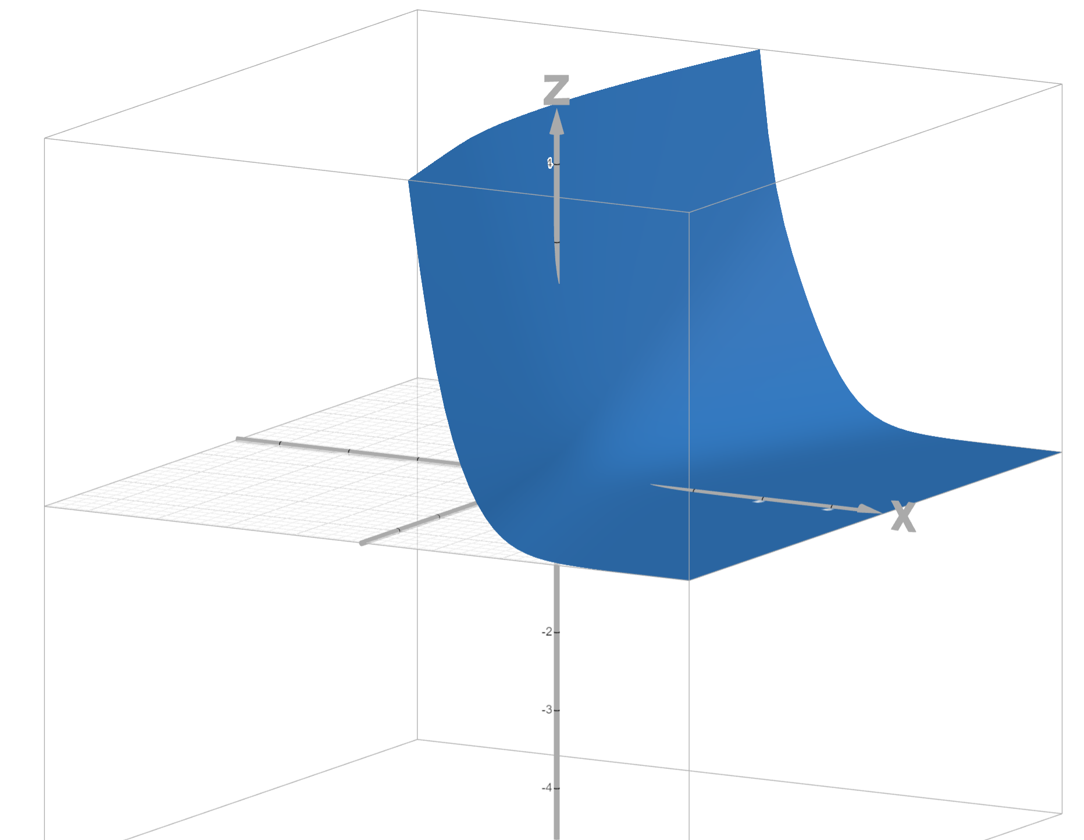
绘制 loss 图像如下,其中 Z 轴为 loss 值,X 轴为 w w w,Y 轴为 b b b。
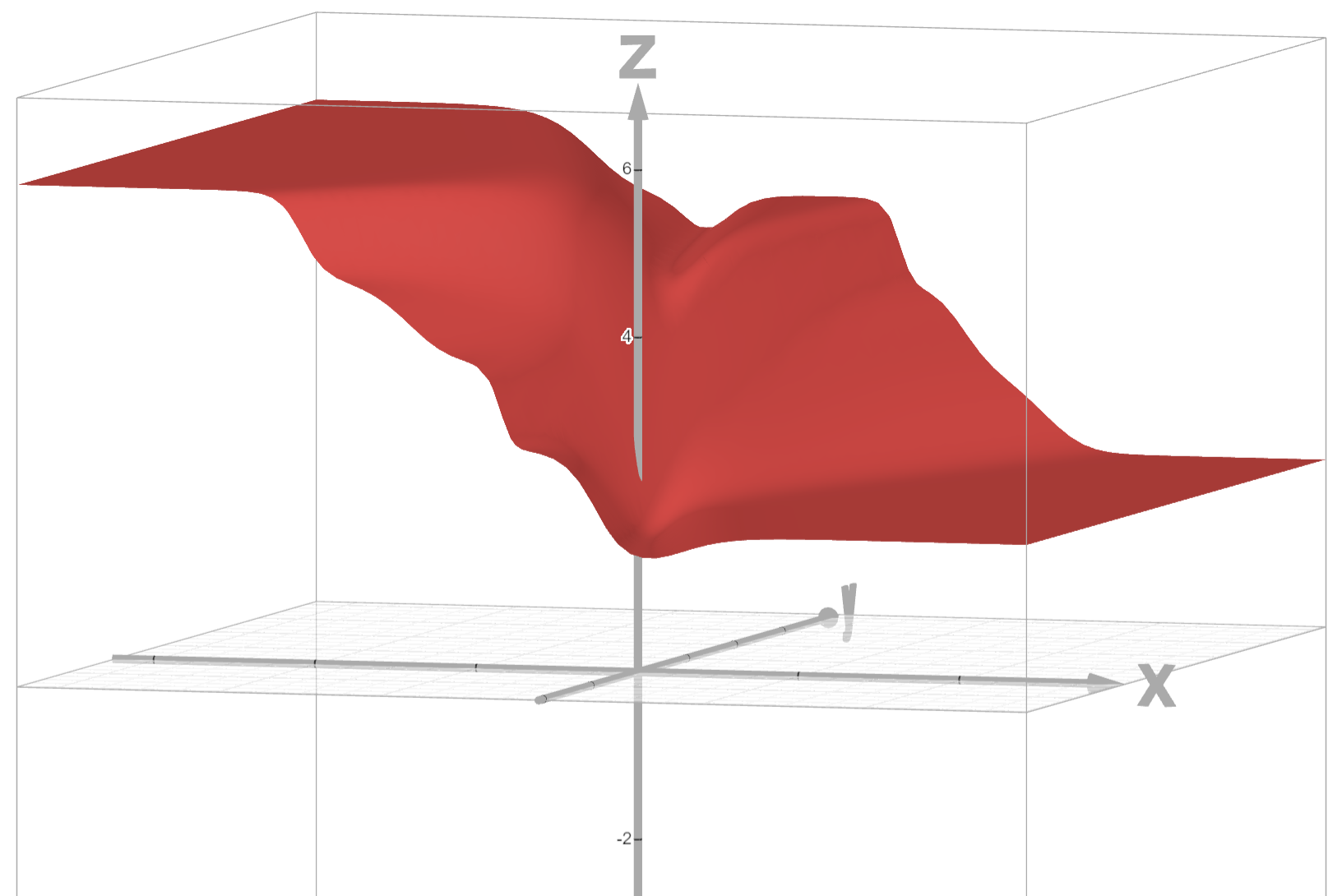
通过观察发现,它是一个 非凸函数 ,也有很多局部最小值 ,训练起来非常不稳定。所以需要给逻辑回归模型寻找其他的损失函数。
交叉熵损失函数
用 y y y 表示 Label 值,用 y ^ \hat y y^ 表示预测值。则二分类交叉熵损失函数 BCELoss(Binary Cross Entropy Loss)分为两种情况。
-
当 y = 1 y=1 y=1 时,
BCELoss = − l o g ( y ^ ) \text{BCELoss} = -log(\hat y) BCELoss=−log(y^)
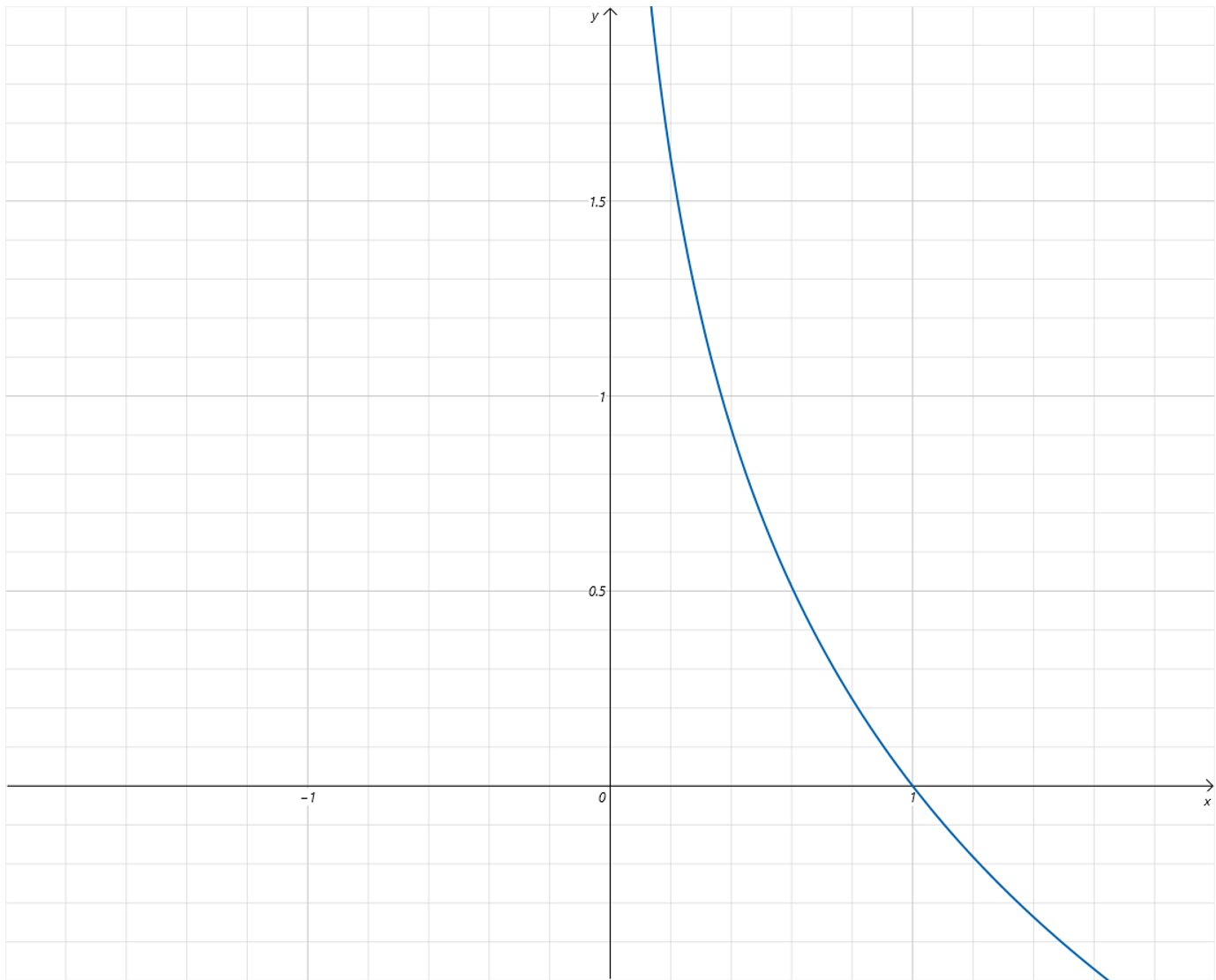
因为 Label 值为
1,预测值为 Sigmoid 函数的输出,取值为从 0 0 0 到 1 1 1。从 Loss 曲线可以看到,当预测值越接近 0 0 0,Loss 值越大,越接近 1 1 1,Loss 值越小。当预测值和 Label 相等,等于1时,Loss 值为 0 0 0。 -
当 y = 0 y=0 y=0 时,
BCELoss = − l o g ( 1 − y ^ ) \text{BCELoss} = -log(1-\hat y) BCELoss=−log(1−y^)
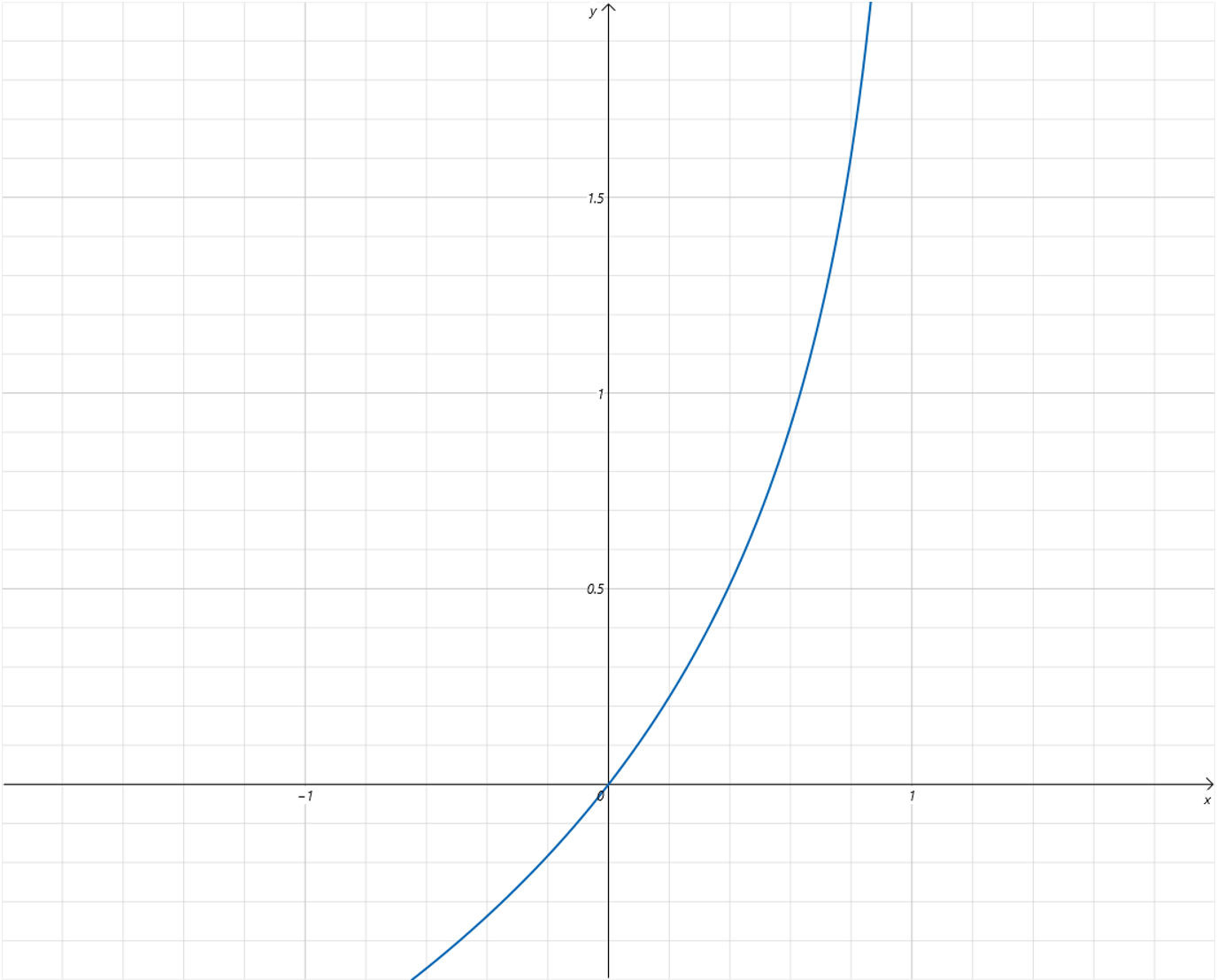
因为 Label 值为
0,预测值为 Sigmoid 函数的输出,取值为从 0 0 0 到 1 1 1。从 Loss 曲线可以看到,当预测值越接近 1 1 1,Loss 值越大,越接近 0 0 0,Loss 值越小。当预测值和 Label 相等,等于0时,Loss 值为 0 0 0。
BCELoss 需要分情况来写,比较麻烦,将它们统一到一个式子里:
BCELoss ( y , y ^ ) = − [ y log y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] \text{BCELoss}(y, \hat y) = - [y \log \hat y + (1 - y) log (1 - \hat y) ] BCELoss(y,y^)=−[ylogy^+(1−y)log(1−y^)]
之前不采用 MSELoss 是因为 它的函数图像不够平滑,那看一下 BCELoss 的函数图像。
可以看到它的 函数图像非常平滑,非常适合用梯度下降来优化。
多元逻辑回归
逻辑回归就是在线性回归的计算结果上,增加了一个 Sigmoid 激活函数。
LogisticRegression ( x ) = Sigmoid ( LinearRegression ( x ) ) = Sigmoid ( w x + b ) \text{LogisticRegression}(x) = \text{Sigmoid}( \text{LinearRegression}(x) ) = \text{Sigmoid}(wx+b) LogisticRegression(x)=Sigmoid(LinearRegression(x))=Sigmoid(wx+b)
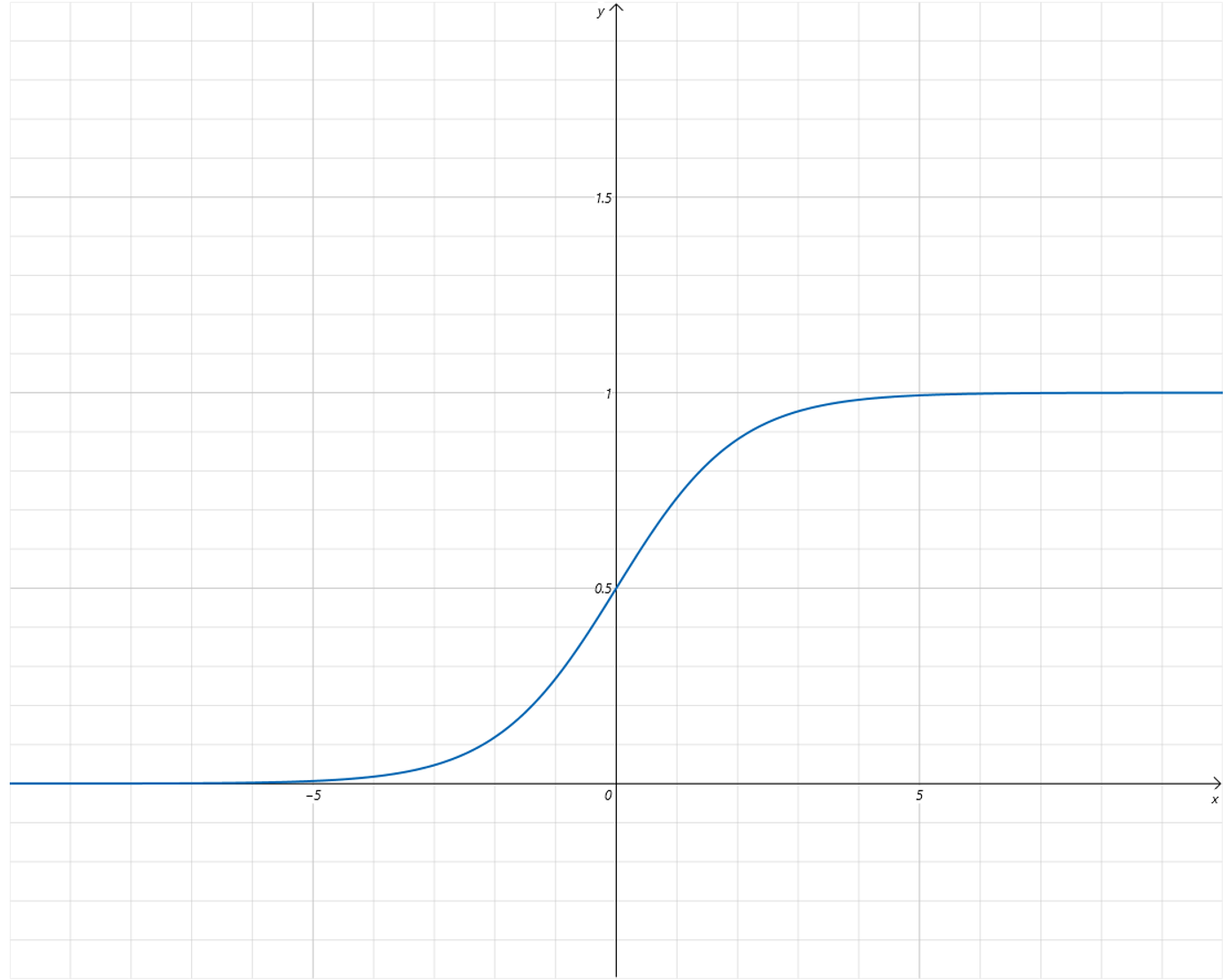
Sigmoid 这个激活函数的作用可以 将大于 0 0 0 的数快速映射到接近 1 1 1,小于 0 0 0 的数快速映射到接近 0 0 0。
在逻辑回归里,Sigmoid 函数的输入是线性回归的结果,所以 线性回归的作用,就是将 Feature 通过参数 w w w 和 b b b 的线性变化,让正例的线性变化结果大于 0 0 0,让负例的线性变化结果小于 0 0 0 。再由 Sigmoid 函数将线性回归的结果映射到 0 − 1 0-1 0−1 之间。
多元逻辑回归,就是 将一元逻辑回归中的一元线性回归部分,升级为多元线性回归,还是对线性回归的结果应用 Sigmoid 激活函数。
LogisticRegression ( x 1 , x 2 , ... , x n ) = Sigmoid ( LinearRegression ( x 1 , x 2 , ... , x n ) ) = Sigmoid ( w 1 x 1 + w 2 x 2 + ... + w n x n + b ) \text{LogisticRegression}(x_1, x_2, \ldots, x_n) = \text{Sigmoid}( \text{LinearRegression}(x_1, x_2, \ldots, x_n)) = \text{Sigmoid}(w_1 x_1 + w_2 x_2 + \ldots + w_n x_n +b) LogisticRegression(x1,x2,...,xn)=Sigmoid(LinearRegression(x1,x2,...,xn))=Sigmoid(w1x1+w2x2+...+wnxn+b)
多元逻辑回归中,
- 多元线性回归部分,将多个 Feature 通过对应的参数 w w w 以及 b b b 进行线性变化 ,让正例的多元线性变化结果大于 0 0 0,让负例的多元线性变化结果小于 0 0 0。
- 最后同样 由 Sigmoid 函数将线性回归的结果映射到 0 0 0 和 1 1 1 之间。
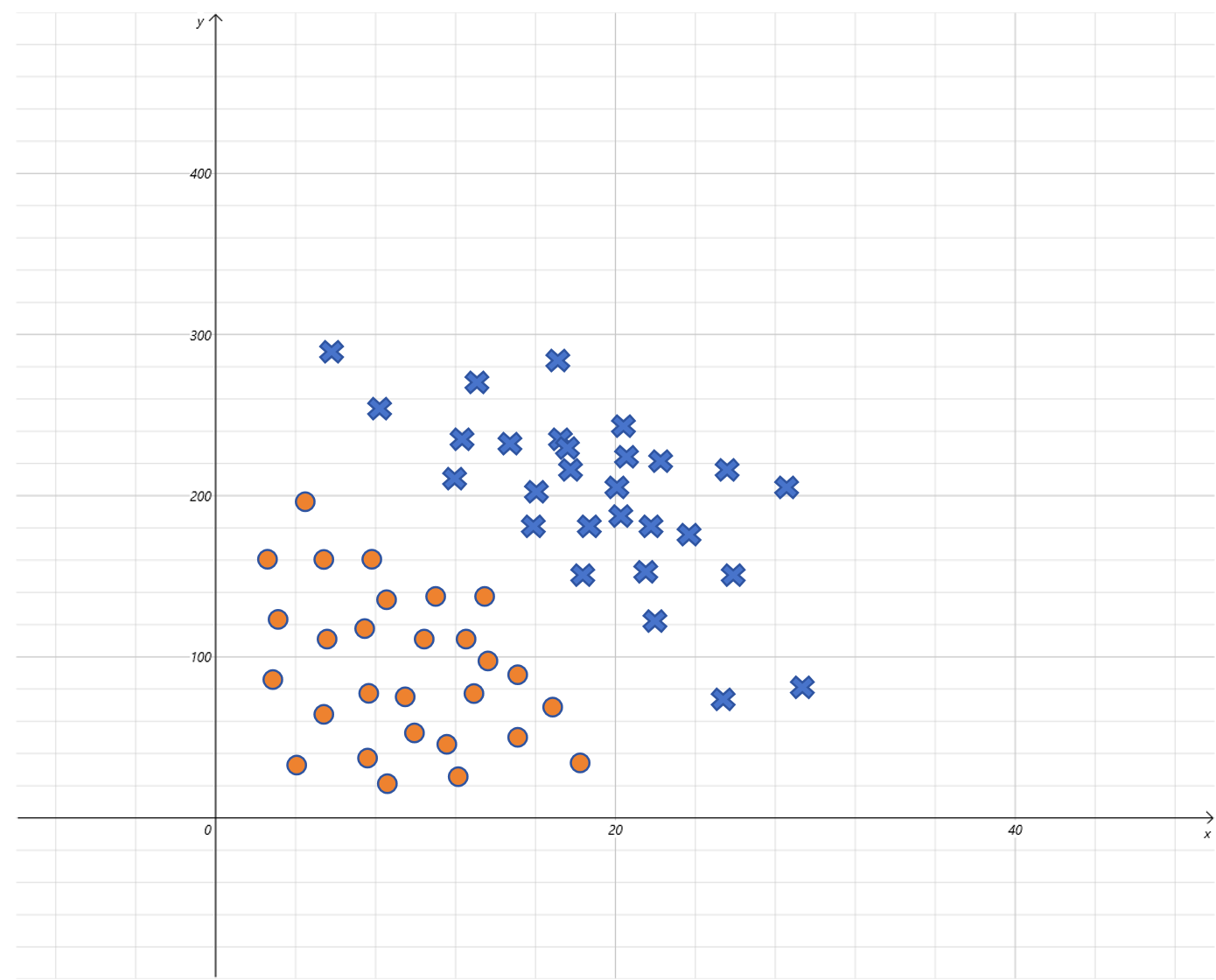
比如上图是小明是否出门与气温( x x x 轴)和 PM2.5( y y y 轴)的关系图。就可以构造一个二元逻辑回归来建模。输入由两个特征气温和 PM2.5 的值,预测出门为 1,不出门为 0。 它的假设函数就为:
Sigmoid ( w 1 x 1 + w 2 x 2 + b ) \text{Sigmoid}(w_1 x_1 + w_2 x_2 + b) Sigmoid(w1x1+w2x2+b)
其中 x 1 x_1 x1 代表气温, w 1 w_1 w1 是气温的权重, x 2 x_2 x2 代表 PM2.5 的值, w 2 w_2 w2 代表 PM2.5 的权重, b b b 是线性回归的偏置。
逻辑回归的决策边界只能是直线吗?
还记得之前 让线性回归拟合曲线 的办法吗?
通过 构造高次项的特征 就可以让线性回归拟合曲线。同样的,这里通过 给逻辑回归里的线性回归部分增加高次项 ,同样可以解决 曲线决策边界 的问题。
Sigmoid ( w 1 x 1 2 + w 2 x 2 2 + b ) \text{Sigmoid}(w_1 x_1^2 + w_2 x_2^2 + b) Sigmoid(w1x12+w2x22+b)
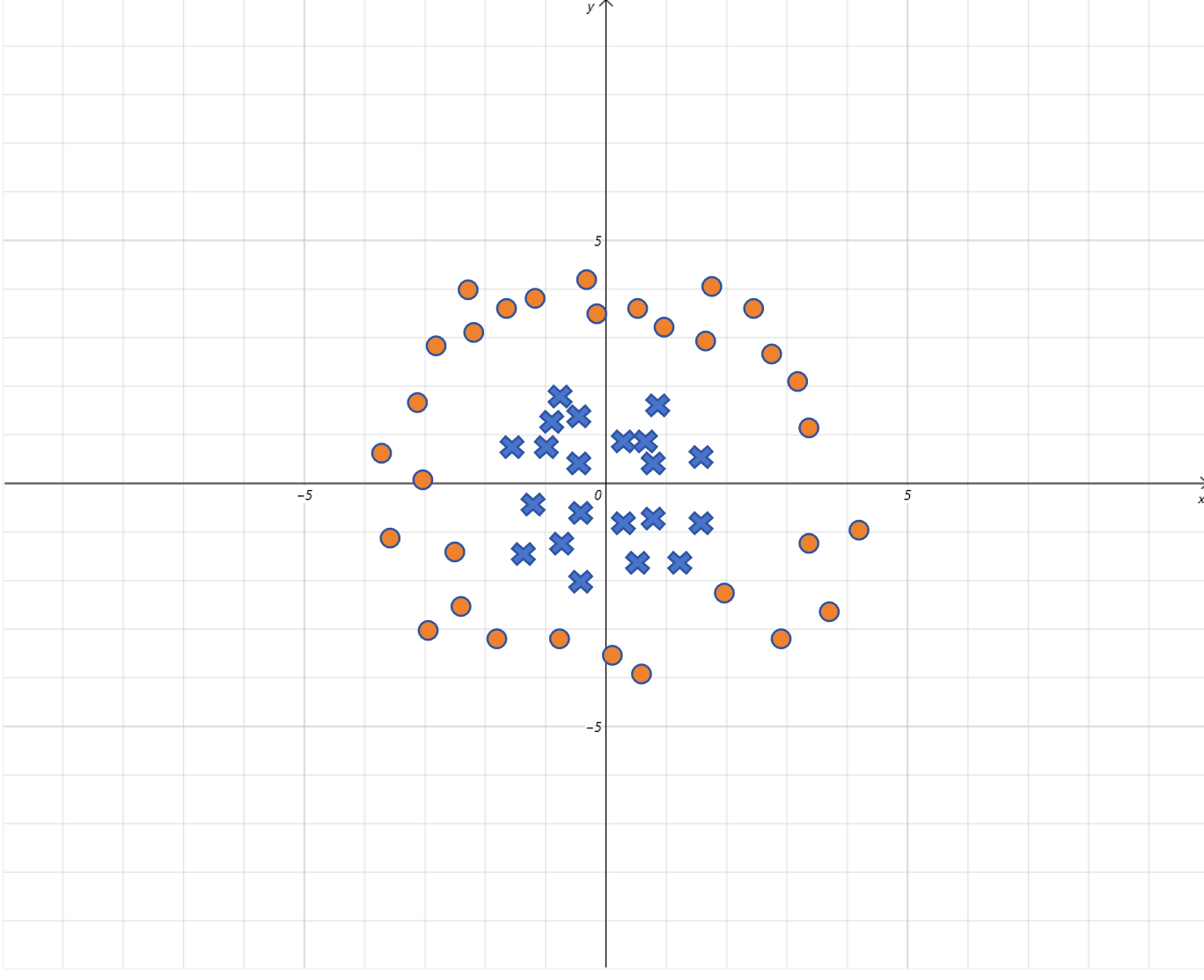
假设通过模型训练,得到 w 1 = 1 , w 2 = 1 , b = − 4 w_1=1,w_2=1,b=-4 w1=1,w2=1,b=−4,代入假设函数, Sigmoid ( x 1 2 + x 2 2 − 2 2 ) \text{Sigmoid}(x_1^2 + x_2^2 - 2^2) Sigmoid(x12+x22−22),
所以 逻辑回归里线性方程就表示一个半径为 2 2 2 的圆,
- 当图上的点在圆的内部,线性方程的取值就小于 0 0 0,被 Sigmoid 函数映射到 0 0 0 附近;
- 当图上的点在圆的外部,线性方程的取值就大于 0 0 0,被 Sigmoid 函数映射到 1 1 1 附近。
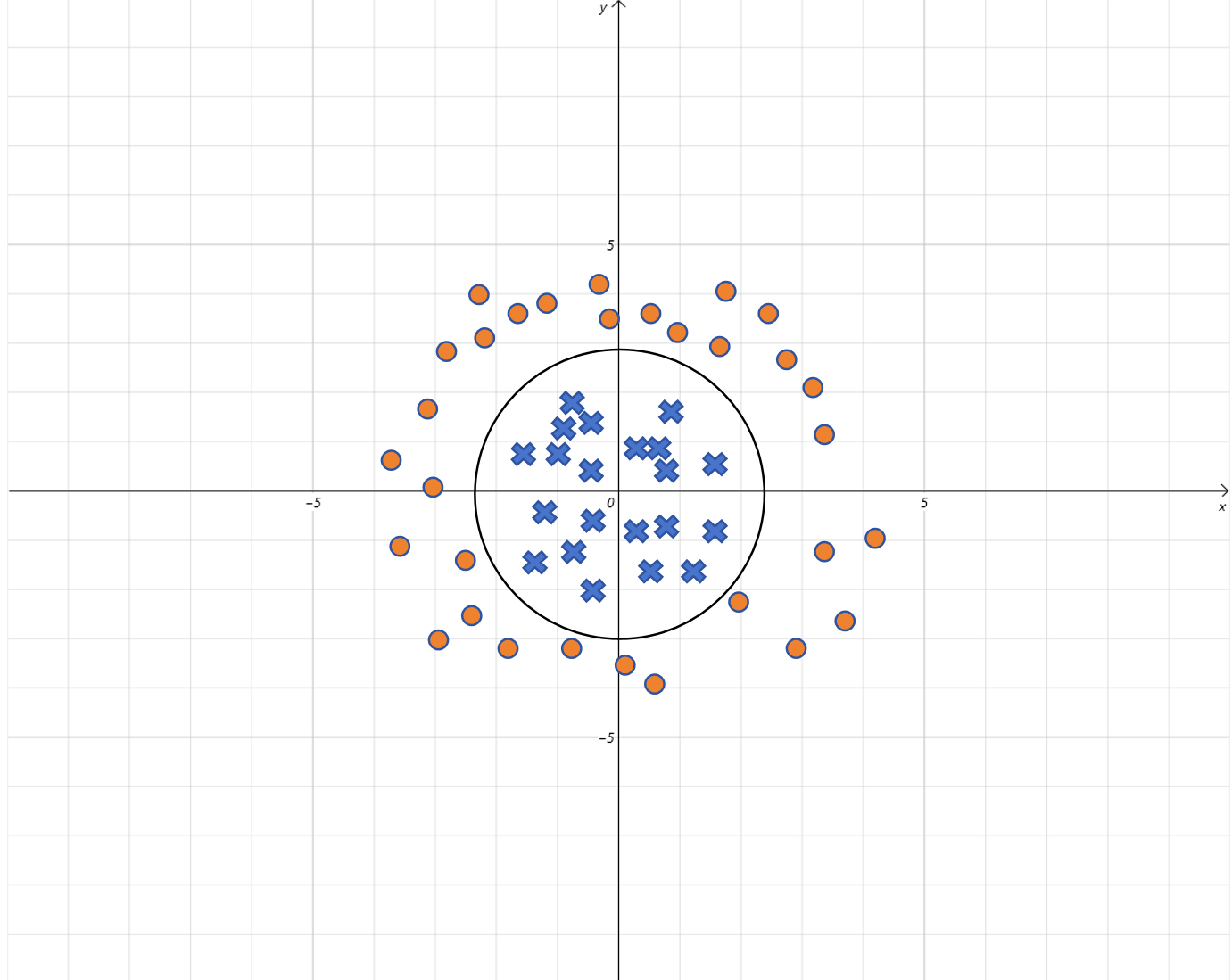
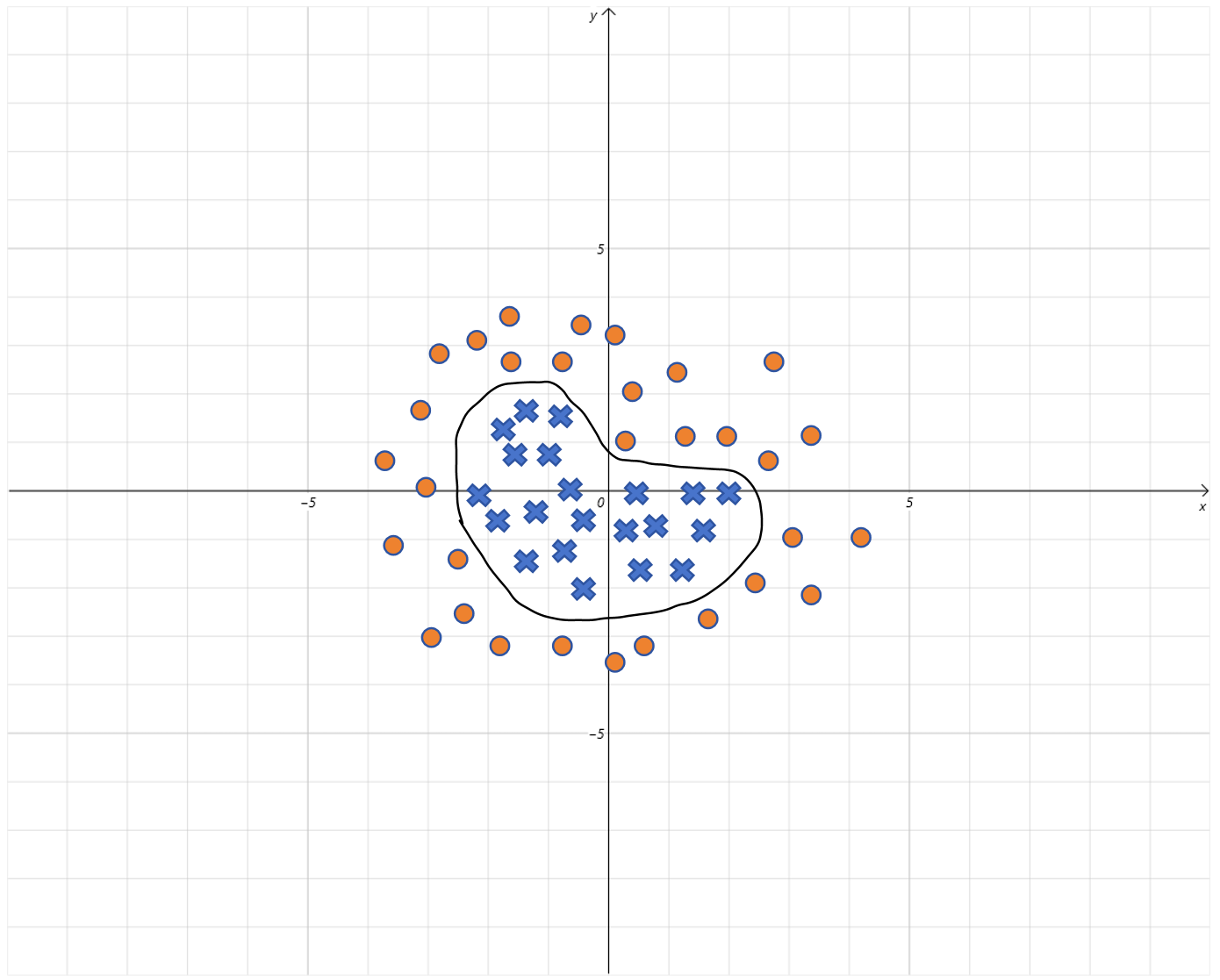
如果增加更多的高次项,理论上逻辑回归的决策边界可以是任意曲线。
逻辑回归只能解决二分类问题吗?
逻辑回归也是可以用来多分类的,最常用的方法,就是 1对多方式。
假如要分类的类别为 A A A, B B B, C C C, D D D。
可以 训练 4 个逻辑回归的模型,它们分别为:
-
区分 A A A 和其他 ( B , C , D ) (B,C,D) (B,C,D) 的二分类模型。以 A A A 为正例,Label 为
1。 -
区分 B B B 和其他 ( A , C , D ) (A,C,D) (A,C,D) 的二分类模型。以 B B B 为正例,Label 为
1。 -
区分 C C C 和其他 ( A , B , D ) (A,B,D) (A,B,D) 的二分类模型。以 C C C 为正例,Label 为
1。 -
区分 D D D 和其他 ( A , B , C ) (A,B,C) (A,B,C) 的二分类模型。以 D D D 正例,Label 为
1。
在预测时,把样本的 feature 分别输入 4 个逻辑回归的模型,可以认为每个模型输出的分别是样本类别为 A A A, B B B, C C C, D D D 的概率值 。取概率值最大的类别作为预测输出 即可。