OpenCASCADE 点云拟合曲线与曲面：从零实现到工业级应用

在现代几何建模与逆向工程中，点云数据的处理是构建精确 CAD 模型的关键环节。OpenCASCADE Technology（OCCT）作为一款功能强大的开源几何建模内核，提供了从离散点集拟合出光滑 B-Spline 曲线与曲面的能力。本文以 OCCT 7.9.0 为背景，结合 Windows 11 + Visual Studio 2022 开发环境，深入剖析 GeomAPI_PointsToBSpline 与 GeomAPI_PointsToBSplineSurface 的使用方法，解决新版 API 变更带来的兼容性问题，并提供可独立运行的完整代码示例。

曲线拟合：从螺旋点云生成 B-Spline 曲线

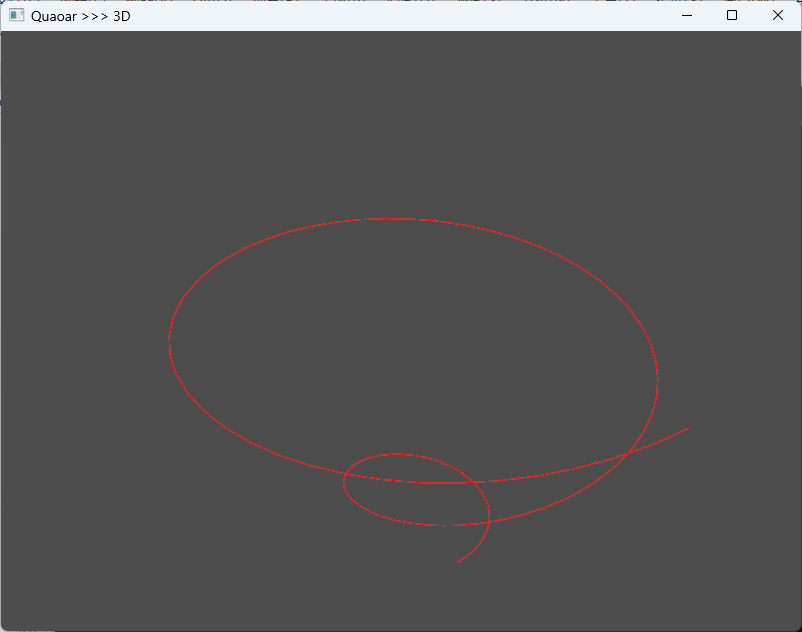
我们首先构造一个典型的三维螺旋线点云，模拟从扫描设备获取的数据。螺旋线的参数方程为：

{x(t)=tcos⁡t10y(t)=tsin⁡t10z(t)=t10,t∈[0,4π] \begin{cases} x(t) = \frac{t \cos t}{10} \\ y(t) = \frac{t \sin t}{10} \\ z(t) = \frac{t}{10} \end{cases}, \quad t \in [0, 4\pi] ⎩ ⎨ ⎧x(t)=10tcosty(t)=10tsintz(t)=10t,t∈[0,4π]

该点云将作为输入，使用 GeomAPI_PointsToBSpline 拟合出一条 C2C^2C2 连续的 B-Spline 曲线。注意在 OCCT 7.9.0 中，GeomAPI_PointsToBSpline 的构造函数接受点数组、最小/最大次数和连续性等级。

cpp 复制代码

// main_curve.cpp
#include <iostream>
#include <vector>
#include <cmath>

// OpenCASCADE 核心头文件
#include <gp_Pnt.hxx>
#include <TColgp_Array1OfPnt.hxx>
#include <TColgp_HArray1OfPnt.hxx>
#include <GeomAPI_PointsToBSpline.hxx>
#include <Geom_BSplineCurve.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <TopoDS_Shape.hxx>

// 可视化封装（假设已实现）
#include "Viewer.h"

int main(int argc, char* argv[])
{
    Viewer vout(50, 50, 800, 600);
    std::vector<TopoDS_Shape> prts;

    // 生成螺旋点云
    std::vector<gp_Pnt> points;
    for (double t = 0; t < 4 * M_PI; t += 0.1) {
        double x = t * cos(t) / 10.0;
        double y = t * sin(t) / 10.0;
        double z = t / 10.0;
        points.emplace_back(x, y, z);
    }

    // 转换为 OCCT 数组
    int nPts = static_cast<int>(points.size());
    Handle(TColgp_HArray1OfPnt) hPoints = new TColgp_HArray1OfPnt(1, nPts);
    for (int i = 0; i < nPts; ++i) {
        hPoints->SetValue(i + 1, points[i]);
    }

    // 拟合 B-Spline 曲线（最小次数 3，最大 8，C2 连续）
    GeomAPI_PointsToBSpline curveFitter(hPoints->Array1(), 3, 8, GeomAbs_C2);
    if (!curveFitter.IsDone()) {
        std::cerr << "曲线拟合失败！" << std::endl;
        return 1;
    }

    Handle(Geom_BSplineCurve) fittedCurve = curveFitter.Curve();
    TopoDS_Edge curveEdge = BRepBuilderAPI_MakeEdge(fittedCurve);
    prts.push_back(curveEdge);

    // 可视化
    for (const auto& shape : prts) {
        vout << shape;
    }
    vout.StartMessageLoop();

    return 0;
}

此代码独立运行后将在窗口中显示一条光滑的螺旋曲线。关键在于 GeomAPI_PointsToBSpline 自动完成了参数化（默认为弦长法）和节点向量生成，用户只需关注输入点集与期望的光滑性。

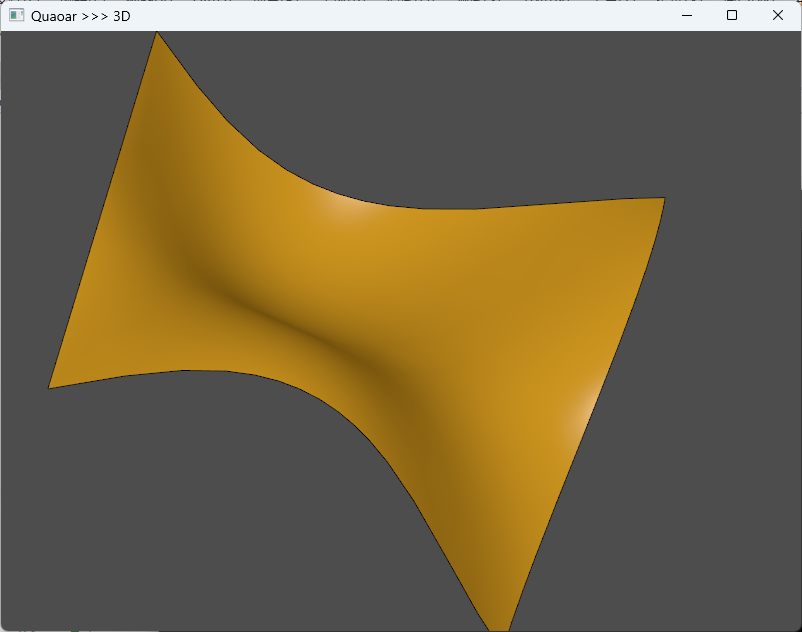
曲面拟合：从网格点云重建 B-Spline 曲面

曲面拟合比曲线更复杂，需处理二维点阵。我们构造一个波浪形曲面，其高度由 z=sin⁡u⋅cos⁡vz = \sin u \cdot \cos vz=sinu⋅cosv 定义，形成 20×2020 \times 2020×20 的规则网格。在 OCCT 7.9.0 中，GeomAPI_PointsToBSplineSurface::Init 的签名已变更，不再接受闭合性标志，而是通过 Approx_ParametrizationType 控制参数化方式。

cpp 复制代码

// main_surface.cpp
#include <iostream>
#include <vector>
#include <cmath>

// OpenCASCADE 核心头文件
#include <gp_Pnt.hxx>
#include <TColgp_Array2OfPnt.hxx>
#include <GeomAPI_PointsToBSplineSurface.hxx>
#include <Geom_BSplineSurface.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#include <TopoDS_Face.hxx>
#include <TopoDS_Shape.hxx>

// 可视化封装
#include "Viewer.h"

int main(int argc, char* argv[])
{
    Viewer vout(50, 50, 800, 600);
    std::vector<TopoDS_Shape> prts;

    // 生成网格点云 (20x20)
    const int nbU = 20, nbV = 20;
    TColgp_Array2OfPnt pointsArray(1, nbU, 1, nbV);

    for (int i = 0; i < nbU; ++i) {
        for (int j = 0; j < nbV; ++j) {
            double u = i * 0.2;
            double v = j * 0.2;
            double x = u;
            double y = v;
            double z = sin(u) * cos(v);
            pointsArray.SetValue(i + 1, j + 1, gp_Pnt(x, y, z));
        }
    }

    // 创建曲面拟合器并初始化
    GeomAPI_PointsToBSplineSurface surfaceFitter;
    surfaceFitter.Init(
        pointsArray,                    // 点阵数据
        Approx_ChordLength,             // 参数化方法：弦长法
        3,                              // 最小次数
        8,                              // 最大次数
        GeomAbs_C2,                     // 连续性要求
        1.0e-3                          // 3D 容差
    );

    if (!surfaceFitter.IsDone()) {
        std::cerr << "曲面拟合失败！" << std::endl;
        return 1;
    }

    // 获取拟合结果（返回 Handle(Geom_BSplineSurface)）
    Handle(Geom_BSplineSurface) fittedSurface = surfaceFitter.Surface();
    TopoDS_Face surfaceFace = BRepBuilderAPI_MakeFace(fittedSurface, 1e-6);
    prts.push_back(surfaceFace);

    // 可视化
    for (const auto& shape : prts) {
        vout << shape;
    }
    vout.StartMessageLoop();

    return 0;
}

此处关键修正点是：

使用 TColgp_Array2OfPnt 而非 Handle(TColgp_HArray2OfPnt)，因为 Init 接受引用而非句柄。
将 Handle(Geom_BoundedSurface) 改为 Handle(Geom_BSplineSurface)，因为 Surface() 方法返回的是具体类型。
参数化类型 Approx_ChordLength 明确指定，避免默认值歧义。

深度解析：OCCT 7.9.0 的 API 变更与数学原理

在 OCCT 7.7 之后，GeomAPI_PointsToBSplineSurface 移除了对闭合性的直接支持，这反映了其设计哲学的转变：拟合与拓扑应分离 。闭合性（周期性）现在需通过后处理实现，例如使用 GeomConvert::SurfaceToBSplineSurface 并调用 SetUNotPeriodic() 或 SetVPeriodic()。

B-Spline 曲面拟合的数学本质是求解一个最小二乘问题。给定点集 ${P_{i,j}} \\in \\mathbb{R}\^3$ ，寻找控制点 ${Q_{k,l}}$ 和节点向量 $U, V$ ，使得：

min⁡∑i,j∥S(ui,vj)−Pi,j∥2 \min \sum_{i,j} \left\| S(u_i, v_j) - P_{i,j} \right\|^2 mini,j∑∥S(ui,vj)−Pi,j∥2

其中 $S(u,v) = \\sum_{k,l} N_{k,p}(u) N_{l,q}(v) Q_{k,l}$ 是 B-Spline 曲面， $N_{k,p}$ 是第 kkk 个 ppp 次基函数。OCCT 使用 chord length 参数化确定 $(u_i, v_j)$ ，即：

ui=∑m=1i∥Pm,j−Pm−1,j∥∑m=1n∥Pm,j−Pm−1,j∥,vj=∑n=1j∥Pi,n−Pi,n−1∥∑n=1m∥Pi,n−Pi,n−1∥ u_i = \frac{\sum_{m=1}^{i} \|P_{m,j} - P_{m-1,j}\|}{\sum_{m=1}^{n} \|P_{m,j} - P_{m-1,j}\|}, \quad v_j = \frac{\sum_{n=1}^{j} \|P_{i,n} - P_{i,n-1}\|}{\sum_{n=1}^{m} \|P_{i,n} - P_{i,n-1}\|} ui=∑m=1n∥Pm,j−Pm−1,j∥∑m=1i∥Pm,j−Pm−1,j∥,vj=∑n=1m∥Pi,n−Pi,n−1∥∑n=1j∥Pi,n−Pi,n−1∥

容差 Tol3DTol3DTol3D 控制拟合精度，通常设为 10−310^{-3}10−3 至 10−610^{-6}10−6，取决于点云密度和模型尺度。

实际应用：从文件读取点云并拟合曲面

在工业场景中，点云通常来自 .txt 或 .ply 文件。以下代码演示如何从文本文件读取 x y z 格式的点并拟合曲面。

cpp 复制代码

// main_from_file.cpp
#include <iostream>
#include <fstream>
#include <vector>
#include <sstream>

#include <gp_Pnt.hxx>
#include <TColgp_Array2OfPnt.hxx>
#include <GeomAPI_PointsToBSplineSurface.hxx>
#include <Geom_BSplineSurface.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#include <TopoDS_Face.hxx>
#include <TopoDS_Shape.hxx>

#include "Viewer.h"

// 假设点云文件为规则网格，每行一个点，按行优先顺序存储
std::vector<std::vector<gp_Pnt>> loadGridFromTxt(const std::string& filename, int rows, int cols)
{
    std::ifstream file(filename);
    if (!file.is_open()) {
        throw std::runtime_error("无法打开文件: " + filename);
    }

    std::vector<std::vector<gp_Pnt>> grid(rows, std::vector<gp_Pnt>(cols));
    double x, y, z;

    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            if (!(file >> x >> y >> z)) {
                throw std::runtime_error("文件数据不足或格式错误");
            }
            grid[i][j] = gp_Pnt(x, y, z);
        }
    }
    file.close();
    return grid;
}

int main(int argc, char* argv[])
{
    Viewer vout(50, 50, 800, 600);

    try {
        // 假设有一个 10x10 的点云文件 "points.txt"
        auto grid = loadGridFromTxt("points.txt", 10, 10);
        int nbU = grid.size(), nbV = grid[0].size();

        TColgp_Array2OfPnt pointsArray(1, nbU, 1, nbV);
        for (int i = 0; i < nbU; ++i) {
            for (int j = 0; j < nbV; ++j) {
                pointsArray.SetValue(i + 1, j + 1, grid[i][j]);
            }
        }

        GeomAPI_PointsToBSplineSurface surfaceFitter;
        surfaceFitter.Init(pointsArray, Approx_ChordLength, 3, 8, GeomAbs_C2, 1e-3);

        Handle(Geom_BSplineSurface) surface = surfaceFitter.Surface();
        TopoDS_Face face = BRepBuilderAPI_MakeFace(surface, 1e-6);
        vout << face;
        vout.StartMessageLoop();

    } catch (const std::exception& e) {
        std::cerr << "错误: " << e.what() << std::endl;
        return 1;
    }

    return 0;
}

此版本增强了鲁棒性，包含文件异常处理，并可通过 MaxDistance() 查询拟合质量。