目录
前言
在探索图的世界时,我们常常面临一个经典问题:从一个起点出发,如何找到通往图中其他所有顶点的"最短"路径?无论是网络路由的数据转发,还是地图导航的路线规划,这个"单源最短路径"问题都是核心所在。
在众多解决方案中,由荷兰计算机科学家Edsger W. Dijkstra提出的Dijkstra算法,无疑是其中最著名、最优雅的算法之一。它像一个有智慧的探索者,每一步都基于当前已知的"最优解"进行扩展,步步为营,最终绘制出一张完整的从起点到各处的最短路径地图。
Dijkstra算法的魅力在于其清晰的贪心策略:它维护一个"已确定最短路径"的集合,并不断地从"未确定"的顶点中挑选一个距离起点最近的顶点加入其中,同时更新其邻居的距离。这个过程如同水波扩散,稳定而可靠。
一、算法概述
Dijkstra算法是解决带权有向图(或无向图) 上单源最短路径问题 的经典贪心算法。由荷兰计算机科学家Edsger W. Dijkstra于1956年提出,其核心思想是通过逐步构建一个最短路径树,来最终确定从源顶点 s 到图中所有其他顶点的最短路径。
该算法要求图中所有边的权值均为非负,这是保证其贪心选择性质成立的关键前提。
Dijkstra算法是为解决最短路径而生,那何为最短路径?
最短路径无非就是两点间的最短距离,
在图的两种类型------网图与非网图中,最短路径这一概念具有不同的含义。在非网图中,由于边不具备权值,最短路径实际上指的是两个顶点之间经过的边数最少的路径,相当于将每条边的权值视为 1。
而在网图中,最短路径则是指两个顶点之间路径上所有边的权值之和最小的那条路径。通常,我们将路径的起始顶点称为源点,路径的最后一个顶点称为终点。
针对带权有向图 G 的最短路径问题,通常可以分为两类:一类是单源最短路径问题,即求解图中某一个顶点到其他所有顶点的最短路径,这类问题可采用经典的 Dijkstra(迪杰斯特拉)算法进行求解;另一类则是多源最短路径问题,即所有顶点对之间的最短路径,通常使用 Floyd(弗洛伊德)算法来求解。
二、核心思想
Dijkstra算法采用贪心策略,通过维护两个集合来逐步构建最短路径树:
集合S :已确定从源点
s到其最短路径的顶点集合。集合V-S:尚未确定最短路径的顶点集合。
算法反复从
V-S中选取一个到源点s距离估计最小 的顶点u,将其加入S,然后对所有以u为起点的边进行松弛操作 。这个过程持续直到V-S为空。实现算法需要两个数组:
dist[]:记录从源点V₀到其他各顶点当前的最短路径长度
初始状态:若V₀与Vᵢ邻接,则dist[i]为边上的权值;否则为∞
path[]:
记录从源点到顶点i的最短路径上的前驱节点,用于回溯完整路径
三、示例讲解
现在有以下这个图:
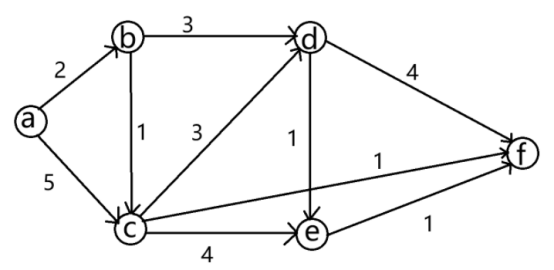
我们用dijkstra算法求a点到各个顶点的最短路径:
列出以下表格:
|-----|-----------|-----------|-------------|-------------|---------------|
| | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| b | 2 (a,b) | | | | |
| c | 5 (a,c) | 3 (a,b,c) | | | |
| d | ∞ | 5 (a,b,d) | 5 (a,b,d) | 5 (a,b,d) | |
| e | ∞ | ∞ | 7 (a,b,c,e) | 7 (a,b,c,e) | 6 (a,b,d,e) |
| f | ∞ | ∞ | 4 (a,b,c,f) | | |
| 终点集 | (a,b) | (a,b,c) | (a,b,c,f) | (a,b,c,f,d) | (a,b,c,f,d,e) |
第一次:
终点集 S={a},dist[a]=0。
从 a出发的直接边:
a→b:2
a→c:5
到 d,e,f 暂无直接边,所以是 ∞。
此时未确定集合 U={b,c,d,e,f},其中距离:
dist[b]=2, dist[c]=5, dist[d]=∞ ,dist[e]=∞ ,dist[f]=∞
此时我们选择最短的距离dist[b]=2 将b加入到终点集中S中,S={a,b}。
第二次:
对 b的邻居进行松弛:
假设 b→c 权为 1:
dist[c]=min(5,2+1)=3,路径变为 a,b,c。
假设 b→d权为 3:
dist[d]=min(∞,2+3)=5,路径 a,b,d。
b→e或 b→f 无边或权大,不更新。
所以第 2 次后:
dist: c=3, d=5, e=∞, f=∞此时我们选择最短的距离dist[c]=3 将b加入到终点集中S中,S={a,b,c}。
第三次
对 c 的邻居松弛:
假设 c→e权为 4:
dist[e]=min(∞,3+4)=7,路径 a,b,c,e。
假设 c→fc权为 1:
dist[f]=min(∞,3+1)=4,路径 a,b,c,f。
c→d可能无边或权大(比如 3+w(c,d)≥5),所以 d 保持 5。
此时:
dist: d=5, e=7, f=4
我们选择最短的距离dist[f]=4 将b加入到终点集中S中,S={a,b,c,f}。
第四次:
对 f的邻居松弛:
从表格看,f 没有更新 e 或 d(可能 f→e权重大于 3,因为 4+w(f,e)≥7不更新;或者 f没有到 e 的边)。
此时:
dist: d=5, e=7
我们选择最短的距离dist[d]=5 将b加入到终点集中S中,S={a,b,c,f,d}。
第五次:
对 dd的邻居松弛:
d→e权为 1:
dist[e]=min(7,5+1)=6,更新路径 a,b,d,e
此时:
dist[e]=6
最后一个选项直接加入终点集,S={a,b,c,f,d,e}。
最后我们得出a点到各个节点的最短距离:
a→b:2
a→c:3(路径 a,b,c)
a→d:5(路径 a,b,d)
a→e:6(路径 a,b,d,e)
a→f:4(路径 a,b,c,f)四、代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#define MAX_NODES 10 // 最大节点数
#define MAX_PATH_LENGTH 20 // 最大路径长度
#define INF INT_MAX // 表示无穷大
typedef struct {
char from; // 边的起始节点
char to; // 边的目标节点
int weight; // 边的权重
} Edge;
typedef struct {
int dist; // 从起点到当前节点的最短距离
char path[MAX_PATH_LENGTH]; // 到当前节点的最短路径
int visited; // 节点是否已访问
} NodeInfo;
// 图的边数据(根据图片权重)
Edge edges[] = {
{'a', 'b', 2}, // a->b的权重为2
{'a', 'c', 5}, // a->c的权重为5 .....
{'b', 'c', 1},
{'b', 'd', 3},
{'c', 'e', 4},
{'c', 'f', 1},
{'c', 'd', 3},
{'d', 'f', 4},
{'d', 'e', 1},
{'e', 'f', 1}
};
int edge_count = sizeof(edges) / sizeof(edges[0]); // 边的数量
// 获取节点索引
int get_index(char node) { // 获取节点的索引(0-9)
return node - 'a'; // 节点a对应索引0,b对应1,以此类推
}
char get_char(int index) { // 获取索引对应的节点字符(a-z)
return 'a' + index; // 索引0对应a,1对应b,以此类推
}
// 安全的路径构建函数
void build_path(char* dest, const char* base_path, char new_node) {
int len = strlen(base_path);
if (len < MAX_PATH_LENGTH - 1) {
strcpy(dest, base_path);
dest[len] = new_node;
dest[len + 1] = '\0';
} else {
strncpy(dest, base_path, MAX_PATH_LENGTH - 1);
dest[MAX_PATH_LENGTH - 1] = '\0';
}
}
// Dijkstra算法
void dijkstra(char start) {
NodeInfo nodes[MAX_NODES]; // 节点信息数组(包含距离、路径、是否访问)
int i;
// 初始化
for (i = 0; i < MAX_NODES; i++) {
nodes[i].dist = INF; // 初始距离设为无穷大
nodes[i].visited = 0; // 初始未访问
nodes[i].path[0] = '\0'; // 初始路径为空
}
int start_idx = get_index(start);
nodes[start_idx].dist = 0; // 起点到自身距离为0
nodes[start_idx].path[0] = start; // 起点路径为自身
nodes[start_idx].path[1] = '\0'; // 路径结束符
printf("起点: %c\n", start);
printf("迭代过程:\n");
printf("------------------------------------------------\n");
int visited_count = 0;
char visited_order[MAX_NODES + 1] = ""; // 已访问节点顺序(初始为空)
int visited_len = 0;
// 添加起点到已访问集合
visited_order[visited_len++] = start;
visited_order[visited_len] = '\0';
while (visited_count < MAX_NODES) { // 当已访问节点数小于最大节点数时
// 从未访问节点中找到距离最小的
int min_dist = INF;
int min_index = -1;
for (i = 0; i < MAX_NODES; i++) {
if (!nodes[i].visited && nodes[i].dist < min_dist) { // 找到未访问节点中距离最小的
min_dist = nodes[i].dist; // 更新最小距离
min_index = i; // 更新最小距离节点索引
}
}
if (min_index == -1) break; // 所有可达节点都已访问
char current_node = get_char(min_index); // 当前节点为距离最小的节点
nodes[min_index].visited = 1; // 标记当前节点为已访问
visited_count++; // 已访问节点数增加
// 更新已访问顺序
if (visited_len < MAX_NODES) {
visited_order[visited_len++] = current_node; // 将当前节点添加到已访问顺序
visited_order[visited_len] = '\0';
}
printf("第%d次迭代:\n", visited_count);
printf("选择节点: %c\n", current_node);
printf("当前距离:\n");
// 打印当前各节点距离(只显示a-f节点,且跳过起点a)
for (i = 0; i < MAX_NODES; i++) {
char node_char = get_char(i);
if (node_char < 'a' || node_char > 'f') continue;
if (node_char == start) continue; // 跳过起点
if (nodes[i].dist == INF) {
printf(" %c: ∞", node_char); // 未访问节点距离为无穷大
} else {
printf(" %c: %d (%s)", node_char, nodes[i].dist, nodes[i].path); // 已访问节点距离和路径
}
if (nodes[i].visited) {
printf(" [已访问]");
}
printf("\n");
}
printf("终点集: {%s}\n", visited_order);
printf("------------------------------------------------\n");
// 更新邻居节点距离
for (i = 0; i < edge_count; i++) {
if (edges[i].from == current_node) { // 如果当前节点为边的起点
int to_idx = get_index(edges[i].to); // 获取目标节点索引
int new_dist = nodes[min_index].dist + edges[i].weight; // 计算新距离
if (new_dist < nodes[to_idx].dist) { // 如果新距离小于目标节点当前距离
nodes[to_idx].dist = new_dist; // 更新目标节点距离
build_path(nodes[to_idx].path, nodes[min_index].path, edges[i].to); // 更新目标节点路径
}
}
}
}
// 打印最终结果
printf("最终最短路径结果:\n");
printf("------------------------------------------------\n");
for (i = 0; i < MAX_NODES; i++) {
char node_char = get_char(i);
if (node_char >= 'a' && node_char <= 'f' && i != start_idx && nodes[i].dist != INF) {
printf("%c -> %c: 距离 = %d, 路径 = %s\n",
start, node_char, nodes[i].dist, nodes[i].path);
}
}
}
int main() {
printf("Dijkstra算法演示\n");
printf("================================================\n");
dijkstra('a');
return 0;
}