以矩阵视角统一理解：外积、Kronecker 积与 Khatri–Rao 积（含MATLAB可视化）

以矩阵视角统一理解：外积、Kronecker 积与 Khatri--Rao 积（含MATLAB可视化）

前言

在信号处理、阵列天线、MIMO 通信、张量分解与机器学习等领域，三类"按块/按列"的乘积------外积（outer product）、Kronecker 积（⊗\otimes⊗）与 Khatri--Rao 积（⊙\odot⊙）频繁出现。它们不仅在数学上彼此关联，也在工程建模与算法推导中相互"勾连"。本文系统梳理三者的定义、维度关系、重要性质、典型恒等式与工程应用 ，并给出MATLAB 实现要点与易错点，

正文

0. 记号与约定

标量域：F∈R,C\mathbb{F}\in{\mathbb{R},\mathbb{C}}F∈R,C。
记号：转置 (⋅)T(\cdot)^{\mathsf T}(⋅)T，共轭转置 (⋅)H(\cdot)^{\mathsf H}(⋅)H，向量化 vec(⋅)\mathrm{vec}(\cdot)vec(⋅)（按列堆叠），Hadamard（逐元素）积记为 ∘\circ∘。
维度：A∈Fm×nA\in\mathbb{F}^{m\times n}A∈Fm×n 表示 mmm 行 nnn 列矩阵；u∈Fmu\in\mathbb{F}^mu∈Fm 表示长度 mmm 的列向量。
外积在复数情形有两种常见用法：
- 非共轭版本：u,vTu,v^{\mathsf T}u,vT（用于张量/代数推导）；
- Hermitian 版本：u,vHu,v^{\mathsf H}u,vH（用于协方差/投影等）。

1. 外积（Outer Product）

定义. 给定 u∈Fm×1u\in\mathbb{F}^{m\times 1}u∈Fm×1、v∈Fn×1v\in\mathbb{F}^{n\times 1}v∈Fn×1，外积是
u⊗1v≜uvT∈Fm×n, u\otimes_1 v \triangleq uv^{\mathsf T}\in\mathbb{F}^{m\times n}, u⊗1v≜uvT∈Fm×n,

其 (i,j)(i,j)(i,j) 元为 uivju_i v_juivj。若用 Hermitian 版本则为 uvHuv^{\mathsf H}uvH。

性质与要点.

秩：rank⁡(uvT)=1\operatorname{rank}(uv^{\mathsf T})=1rank(uvT)=1（当 u,v≠0u,v\neq 0u,v=0）。
张量构造：一阶向量外积可堆叠生成高阶秩一张量（CP 分解的原子）。
协方差模型 ：R=hhH+σ2IR=hh^{\mathsf H}+\sigma^2 IR=hhH+σ2I 中的信号部分是外积。

2. Kronecker 积（A⊗BA\otimes BA⊗B）

定义. A∈Fm×nA\in\mathbb{F}^{m\times n}A∈Fm×n、B∈Fp×qB\in\mathbb{F}^{p\times q}B∈Fp×q，
A⊗B=[a11B⋯a1nB⋮⋱⋮am1B⋯amnB]∈F(mp)×(nq). A\otimes B=\begin{bmatrix} a_{11}B & \cdots & a_{1n}B\\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{mn}B \end{bmatrix}\in\mathbb{F}^{(mp)\times (nq)}. A⊗B= a11B⋮am1B⋯⋱⋯a1nB⋮amnB ∈F(mp)×(nq).

核心性质.

双线性与结合律 ：(αA+βC)⊗B=α(A⊗B)+β(C⊗B)(\alpha A+\beta C)\otimes B=\alpha(A\otimes B)+\beta(C\otimes B)(αA+βC)⊗B=α(A⊗B)+β(C⊗B)；(A⊗B)⊗C=A⊗(B⊗C)(A\otimes B)\otimes C=A\otimes(B\otimes C)(A⊗B)⊗C=A⊗(B⊗C)。
混合乘积恒等式（mixed-product） ：当维度可乘时
(A⊗B)(C⊗D)=(AC)⊗(BD). (A\otimes B)(C\otimes D)=(AC)\otimes (BD). (A⊗B)(C⊗D)=(AC)⊗(BD).
向量化恒等式（极其重要） ：
vec(AXBT)=(B⊗A)vec(X),vec(AXBH)=(B‾⊗A)vec(X). \mathrm{vec}(A X B^{\mathsf T})=(B\otimes A)\mathrm{vec}(X),\qquad \mathrm{vec}(A X B^{\mathsf H})=(\overline{B}\otimes A)\mathrm{vec}(X). vec(AXBT)=(B⊗A)vec(X),vec(AXBH)=(B⊗A)vec(X).

这在线性方程矢量化 、最小二乘 与高维协方差建模中广泛使用。
特征结构 ：若 AAA 与 BBB 的特征值分别为 λi{\lambda_i}λi、μj{\mu_j}μj，则 A⊗BA\otimes BA⊗B 的特征值为 λiμj{\lambda_i\mu_j}λiμj（在适当可对角化条件下）。

工程直觉. Kronecker 将"一个系数乘以一个整块 "并拼接，体现张量/块结构放大 ------例如二维相关建模可分离为行/列相关的 Kronecker 近似（阵列-时域的可分结构）。

3. Khatri--Rao 积（按列的 Kronecker，A⊙BA\odot BA⊙B）

定义. 设 A∈Fm×rA\in\mathbb{F}^{m\times r}A∈Fm×r、B∈Fn×rB\in\mathbb{F}^{n\times r}B∈Fn×r 列数一致，
A⊙B=[A:1⊗B:1;A:2⊗B:2;... ;A:r⊗B:r]∈F(mn)×r. A\odot B = \big[A_{:1}\otimes B_{:1}; A_{:2}\otimes B_{:2};\dots;A_{:r}\otimes B_{:r}\big]\in\mathbb{F}^{(mn)\times r}. A⊙B=[A:1⊗B:1;A:2⊗B:2;...;A:r⊗B:r]∈F(mn)×r.

它将同列的两个向量做 Kronecker，然后把这些列并排起来，故又称"列 Kronecker"。

关键性质.

Gram 恒等式 + Schur 定理 ：
(A⊙B)T(A⊙B)=(ATA)∘(BTB). (A\odot B)^{\mathsf T}(A\odot B) = (A^{\mathsf T}A)\circ (B^{\mathsf T}B). (A⊙B)T(A⊙B)=(ATA)∘(BTB).

由 Schur（Hadamard）乘积定理可知：若 AAA、BBB 满列秩 ，则右端为正定，故 A⊙BA\odot BA⊙B 满列秩。这对可辨识性与稳健求解至关重要。
与 Kronecker/向量化的关系 （块选择视角）：
A⊙B=(Ir⊗B)Π(Ir⊗A), A\odot B = (I_r \otimes B)\Pi (I_r \otimes A), A⊙B=(Ir⊗B)Π(Ir⊗A),

其中 Π\PiΠ 为恰当的块/置换算子；直观含义是"先做 Kronecker，再取同列"。
在 CP/CPD 分解中的角色 ：CP 分解的正规方程与雅可比/高斯--牛顿步常出现
(C⊙B)T(C⊙B)=(CTC)∘(BTB), (C\odot B)^{\mathsf T}(C\odot B)=(C^{\mathsf T}C)\circ(B^{\mathsf T}B), (C⊙B)T(C⊙B)=(CTC)∘(BTB),

使得求解可分解为若干小维度的 Hadamard-缩放问题，降低复杂度。

4. 三者的联系与差异（一图胜千言的"维度/结构表"）

运算	输入	输出尺寸	结构直觉	典型用途
外积 uvTuv^{\mathsf T}uvT	u∈Fm×1u\in\mathbb{F}^{m\times1}u∈Fm×1，v∈Fn×1v\in\mathbb{F}^{n\times1}v∈Fn×1	m×nm\times nm×n	秩一平面，元素为两向量逐元素"相乘并铺开"	秩一近似、协方差建模、投影
Kronecker A⊗BA\otimes BA⊗B	A∈Fm×nA\in\mathbb{F}^{m\times n}A∈Fm×n，B∈Fp×qB\in\mathbb{F}^{p\times q}B∈Fp×q	(mp)×(nq)(mp)\times(nq)(mp)×(nq)	块放大/拼接	2D 可分模型、向量化恒等式、图像/阵列处理
Khatri--Rao A⊙BA\odot BA⊙B	A∈Fm×rA\in\mathbb{F}^{m\times r}A∈Fm×r，B∈Fn×rB\in\mathbb{F}^{n\times r}B∈Fn×r	(mn)×r(mn)\times r(mn)×r	列对齐的 Kronecker	张量 CP/CPD、MIMO 维纳/LS、并行因子模型

5. 在通信/信号处理中的典型图景

MIMO 信道的 Kronecker 相关模型 ：R≈Rrx⊗RtxR\approx R_{\text{rx}}\otimes R_{\text{tx}}R≈Rrx⊗Rtx，把二维相关分解为接收/发射两侧相关（可分结构）。
多维导向向量 ：二维阵列（水平×垂直）导向向量常写作 a(θ,ϕ)=ah(θ)⊗av(ϕ)a(\theta,\phi)=a_{\text{h}}(\theta)\otimes a_{\text{v}}(\phi)a(θ,ϕ)=ah(θ)⊗av(ϕ)。
CP/并行因子（PARAFAC）建模 ：多维测量张量 X≈∑r=1Rar∘br∘cr\mathcal{X}\approx\sum_{r=1}^R a_r\circ b_r\circ c_rX≈∑r=1Rar∘br∘cr，其法方程 与雅可比 都包含 A⊙BA\odot BA⊙B。
矢量化线性化 ：vec(AXBT)=(B⊗A)vec(X)\mathrm{vec}(A X B^{\mathsf T})=(B\otimes A)\mathrm{vec}(X)vec(AXBT)=(B⊗A)vec(X) 让二维滤波/变换化为一维乘法，便于最小二乘与稀疏求解。

6. 复杂度与数值注意事项

维度爆炸 ：A⊗BA\otimes BA⊗B 的尺寸是 (mp)×(nq)(mp)\times(nq)(mp)×(nq)，随维度 乘法级 放大；实现时应尽量避免显式形成大矩阵，优先用恒等式（如 vec-恒等式）隐式计算。
条件数 ：Kronecker 的条件数满足 κ(A⊗B)=κ(A),κ(B)\kappa(A\otimes B)=\kappa(A),\kappa(B)κ(A⊗B)=κ(A),κ(B)（在相容范数下），警惕数值不稳定的放大效应。
Khatri--Rao 的满秩性 ：由 Gram 恒等式与 Schur 定理可知，AAA、BBB 满列秩 ⇒A⊙B\Rightarrow A\odot B⇒A⊙B 满列秩，这对最小二乘/正则化的可解性与唯一性判断很关键。
复数场 ：注意 (⋅)T(\cdot)^{\mathsf T}(⋅)T 与 (⋅)H(\cdot)^{\mathsf H}(⋅)H 的选择与物理语义（是否需要共轭）；例如外积在协方差中通常使用 (⋅)H(\cdot)^{\mathsf H}(⋅)H。

7. MATLAB 可视化

matlab 复制代码

%% viz_products.m

% 可视化 outer product、Kronecker product、Khatri--Rao product

clear; clc; close all;

%% ========= 1) 外积 Outer Product =========

% u ∈ C^{m×1}, v ∈ C^{n×1}, 外积 u * v.' -> m×n（用 .', 避免共轭）

u = (1:3).'; % 3×1

v = (10:10:40).'; % 4×1

Outer = u * v.'; % 3×4

figure('Name','Outer Product','Color','w');

tiledlayout(1,3,'Padding','compact','TileSpacing','compact');

nexttile; showMatrix(u, 'u (3×1)');

nexttile; showMatrix(v.', 'v^T (1×4)');

nexttile; showMatrix(Outer, 'Outer = u·v^T (3×4)');

%% ========= 2) Kronecker 积 =========

% A ⊗ B：将 A 的每个元素 a_ij 作为系数，乘以矩阵 B，形成对应的块并拼接

A = [ 1 2; % 2×2

3 4 ];

B = [ 5 6 7; % 3×3

8 9 10;

11 12 13 ];

K = kron(A, B); % 6×6

figure('Name','Kronecker Product','Color','w');

tiledlayout(1,3,'Padding','compact','TileSpacing','compact');

nexttile; showMatrix(A, 'A (2×2)');

nexttile; showMatrix(B, 'B (3×3)');

axK = nexttile; showMatrix(K, 'kron(A,B) (6×6)');

drawKronBlockGrid(axK, size(A), size(B)); % 画出块分隔线

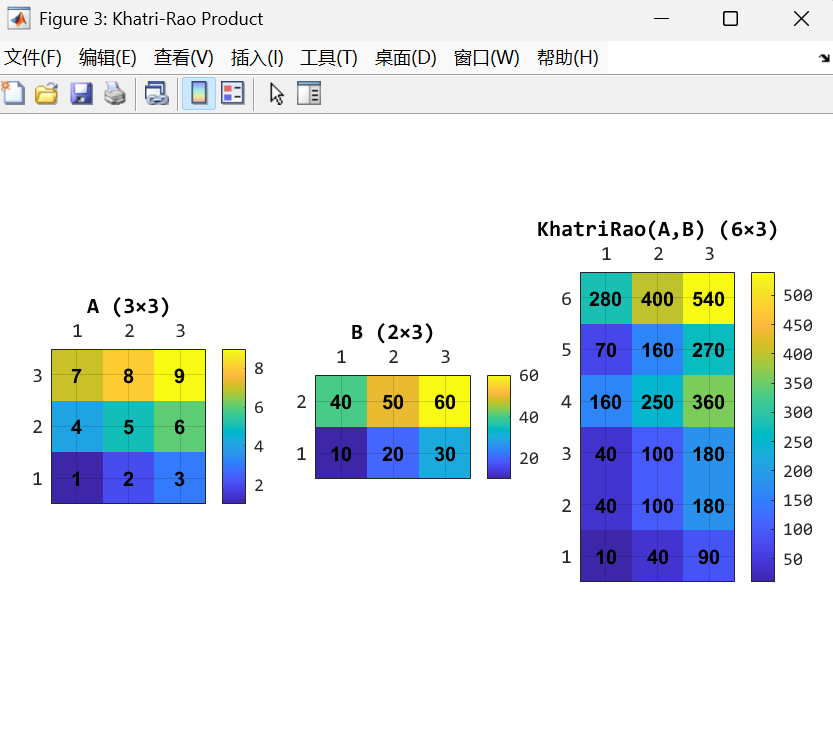
%% ========= 3) Khatri--Rao 积（按列的 Kronecker 积）=========

% 设 A ∈ R^{m×r}, B ∈ R^{n×r}，则

% KhatriRao(A,B) = [ kron(A(:,1),B(:,1)), ..., kron(A(:,r),B(:,r)) ] ∈ R^{mn×r}

Akr = [ 1 2 3; % 3×3

4 5 6;

7 8 9 ];

Bkr = [10 20 30; % 2×3（列数需与 Akr 一致）

40 50 60];

KR = khatri_rao(Akr, Bkr); % 6×3

figure('Name','Khatri-Rao Product','Color','w');

tiledlayout(1,3,'Padding','compact','TileSpacing','compact');

nexttile; showMatrix(Akr, 'A (3×3)');

nexttile; showMatrix(Bkr, 'B (2×3)');

nexttile; showMatrix(KR, 'KhatriRao(A,B) (6×3)');

%% ================== 辅助函数 ==================

function KR = khatri_rao(A, B)

%KHATRI_RAO 按列的 Kronecker 积

% 输入: A(m×r), B(n×r) ------ 列数 r 必须相同

% 输出: KR(mn×r)，第 k 列为 kron(A(:,k), B(:,k))

[m, rA] = size(A);

[n, rB] = size(B);

if rA ~= rB

error('Khatri-Rao: A 与 B 的列数必须相同。got A:%dx%d, B:%dx%d', m, rA, n, rB);

end

% 使用 superiorfloat 选择更高精度类型分配（避免 A+B 尺寸不兼容的错误）

KR = zeros(m*n, rA, superiorfloat(A, B));

for k = 1:rA

KR(:,k) = kron(A(:,k), B(:,k));

end

end

function showMatrix(M, ttl)

%SHOWMATRIX 彩色图 + 单元格数值标注

imagesc(M);

axis equal tight;

colormap(parula); colorbar;

title(sprintf('%s', ttl), 'FontWeight','bold');

% 设置网格/刻度以对齐单元格

[r,c] = size(M);

set(gca,'XTick',1:c,'YTick',1:r,'TickLength',[0 0], ...

'XAxisLocation','top','YDir','normal','FontName','Consolas','FontSize',10);

grid on;

% 画浅网格线

ax = gca;

ax.GridColor = [0 0 0];

ax.GridAlpha = 0.15;

% 标注数值

hold on;

for i = 1:r

for j = 1:c

val = M(i,j);

if isreal(val)

% 这里用 .0f；如需小数可改成 %.2f

txt = sprintf('%.0f', val);

else

txt = sprintf('%.1f%+,.1fi', real(val), imag(val));

end

text(j, i, txt, ...

'HorizontalAlignment','center','VerticalAlignment','middle', ...

'FontWeight','bold','Color','k','Interpreter','none');

end

end

hold off;

end

function drawKronBlockGrid(ax, szA, szB)

%DRAWKRONBLOCKGRID 在 kron(A,B) 图上叠加块分隔线

% szA = size(A) = [p q], szB = size(B) = [r s]

% 则 kron(A,B) 的块尺寸为 r×s，共 p×q 个块

if nargin < 1 || isempty(ax), ax = gca; end

axes(ax); hold on;

p = szA(1); q = szA(2);

r = szB(1); s = szB(2);

xMax = q*s; yMax = p*r;

% 竖线

for k = 1:q-1

x = 0.5 + k*s;

plot([x x], [0.5 yMax+0.5], '-', 'LineWidth', 1.2, 'Color', [1 1 1]);

end

% 横线

for k = 1:p-1

y = 0.5 + k*r;

plot([0.5 xMax+0.5], [y y], '-', 'LineWidth', 1.2, 'Color', [1 1 1]);

end

hold off;

end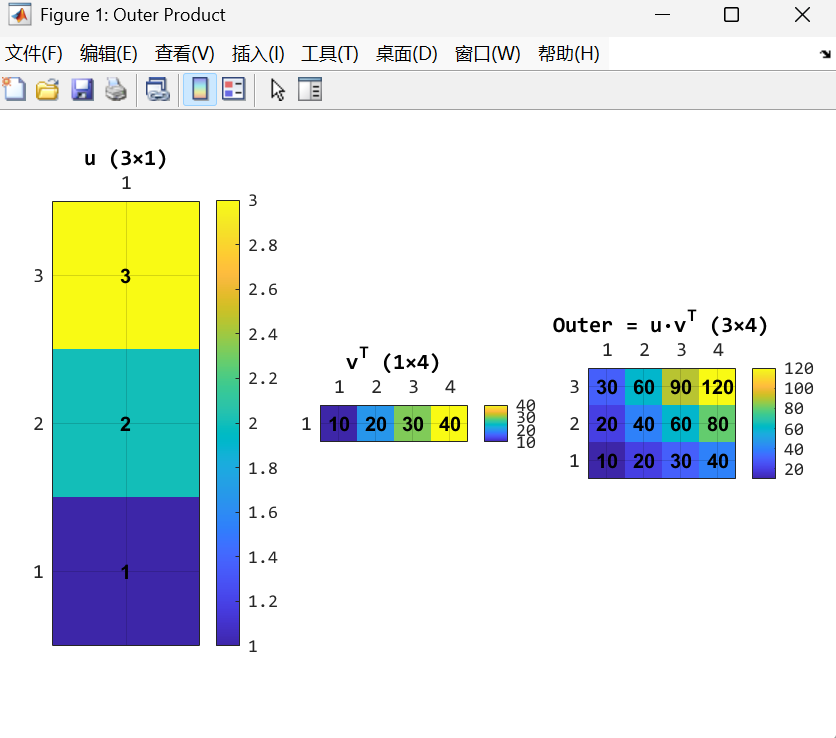

总结

外积、Kronecker 积与 Khatri--Rao 积构成了从秩一到块结构再到列对齐的层级体系：

外积是秩一构件，是张量分解的最小"原子"；
Kronecker 将二维/多维结构分离并以块方式放大，配合 vec\mathrm{vec}vec 恒等式成为高维线性化的基石；
Khatri--Rao 通过"按列 Kronecker "在张量因子化与法方程中扮演枢纽角色，其 Gram--Hadamard 恒等式直接给出满列秩与数值稳定性的判据。

在工程实践中，建议优先思考结构化恒等式 （而非显式构造巨型矩阵），并在论文中明确：维度、恒等式引用、复杂度评估与数值细节（转置/共轭、满秩条件、正则化）。如此既能保证理论表述的严谨 ，也能在实现层面获得高效与稳健的收益。