文章目录
当你迷茫的时候,请点击 目录大纲 快速查看前面的技术文章,相信你总能找到前行的方向
L1范数最值问题
上文 有一题比较有意思,求 |x-1|+|x-2|+|x-3|+...|x-n| 在什么时候取最小值,更高深的叫法是 L1范数 求最值
本文我们继续来探索一下这个式子的其他意义,也许会有不同的发现和解法
绝对值概念
绝对值,也叫绝对值函数,是数学中一个重要的函数,它将一个实数映射到实数上,并且绝对值的结果一定为非负数(即 0 或正数),这个只是单纯的从数值角度上来表述的,说白了就是只有负数的绝对值就是要加个负号而已
其实,绝对值还有它的几何意义,那就是距离,表示两个点相差多少或者说相隔多远,比较两个数相差多少,通常用减法,两个数相减得出差值,差值 = 大数 - 小数
比如说小明考90分,小丽考95分,小强考100分,那我们会说小明与小丽相差5分,小强与小丽之间也相差5分,相差5分是一个很模糊的说法,不代表小明与小强考的分数一样多,相差5分就是绝对值的含义。
同样道理,在数轴上有两个数字,分别是数字a与 数字b,它们之间的距离就是| a-b|,表示 a 与 b 之间相差多少
更特殊地,某个数字x 到 数字0 的距离为 |x - 0|=|x|,可以表示为x 与 0 之间相差多少,即是 x 的绝对值
举例说明:
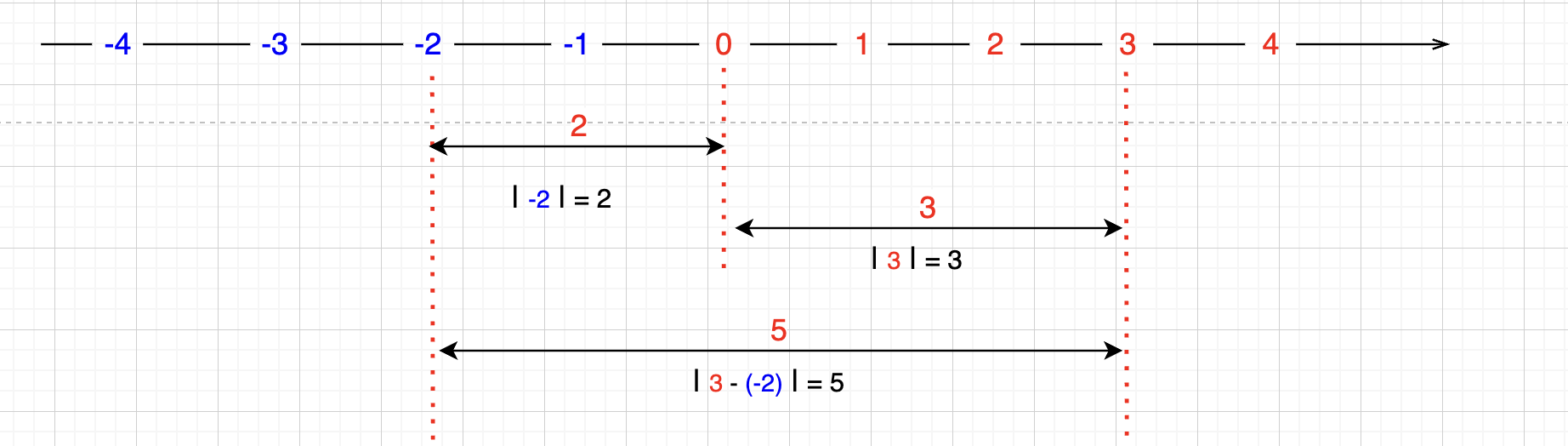
|-2| = |-2 - 0 | = 2,即 -2 到 0 的距离是 2
| 3 | =|3 - 0 | = 3,即 3 到 0 的距离是 3
|3 - (-2)|= 5,即 3 到 -2 的距离是 5
现实的距离
现实中的距离,一般是说两点间直线距离,就是两点间隔了有多远,它是一段长度,永远是大于等于0的。如果我问你,你家到学校的距离有多远,你会回答1公里,不可能说是负1公里吧?
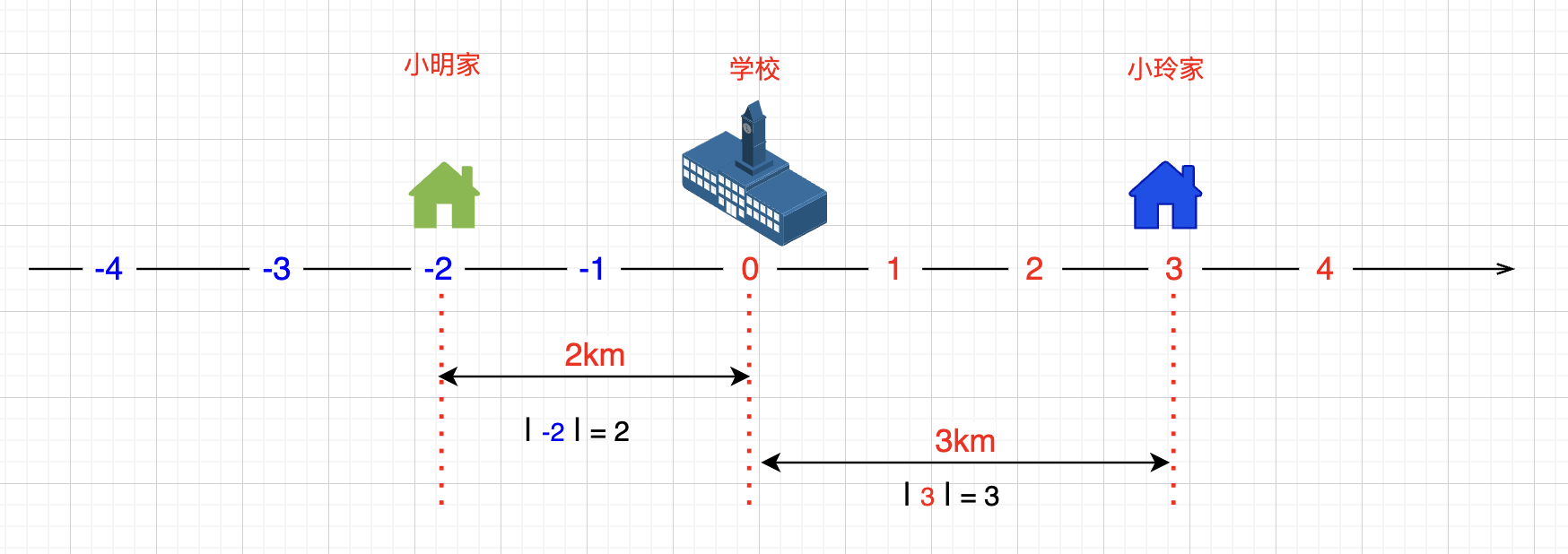
我们可以把数轴比作马路,每个数就像是一个地点,0点就像是学校,小明家住在 -2 点上,小玲家住在 3 点上,那么小明家到学校的距离是|-2 - 0|= 2公里,小玲家到学校是 |3 - 0|= 3公里。
那举一反三:小玲家(3点) 到小明家(-2点)之间的距离是多远?当然就等于|3 - (-2)|= 5 公里,我们可以直接相减得出,这是最快的。
这里可以下结论说:绝对值就是距离,距离就是绝对值
建学校的问题
学校怎么建才好呢,当然是离家越近越好,但每个同学住的地方不一样,不可能人人都住在学校旁边,那么学校到底建的好不好呢?
我们可以用所有同学家到学校的距离之和来评判,总距离越小,那学校就建的好,对大家来说相对公平。
比如上面的学校建在了0点处,我以学校的角度来看,小明家距离学校是 2km,小玲家距离学校是 3km,那总距离是|0 - (-2)|+|0 - 3|= 2 + 3 = 5 km,而且两位同学的路线没有重合

如果我学校建在了4点位置呢?
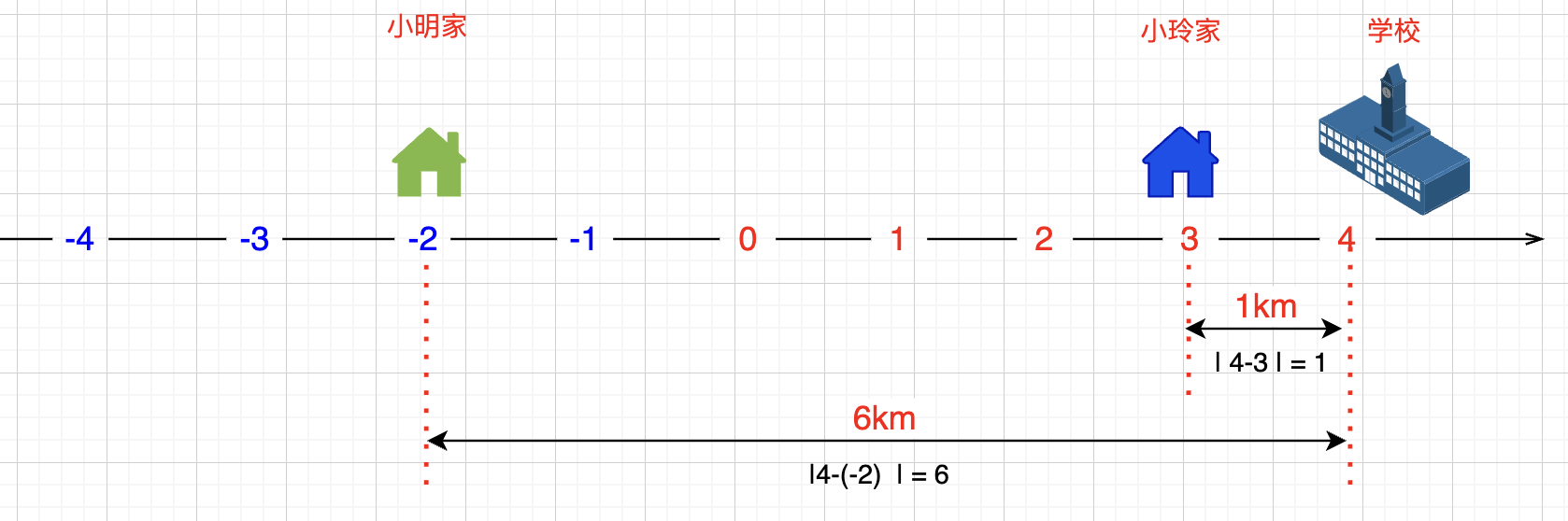
学校离小玲家近了(1km),但离小明家就远了(6km),总距离就是 |4 - 3|+|4 - (-2)|= 1+6 = 7km,对比上面的5km 是不是多了2km?
原因就是学校建的位置不好,两位同学走的路线有重合的地方,就是 3 到 4 之间的路段为 1km,两位同学都要多走这 1km,那就是多走了 2km,多出的的 2km 就出在这里
所以,要想学校建的好,就要总距离少,就是让各位同学路线减少重合,就会避免同学们多走路
按照上面的思路,每个同学例如住在a点,他到学校的距离就是 |x - a|=|a - x|,假如每个整数点都住了了一位同学(1,2,3,4...),学校建在了某个点x上,总距离会不会求?
总距离 = |x-1|+|x-2|+|x-3|+|x-4|...
举个例子,假设学校还是建在0点,当n=4时,即有4个同学分别住在 1,2,3,4 点上,那么总距离就如下图所示,总距离 = |0-1|+|0-2|+|0-3|+|0-4| = 1+2+3+4 = 10 km
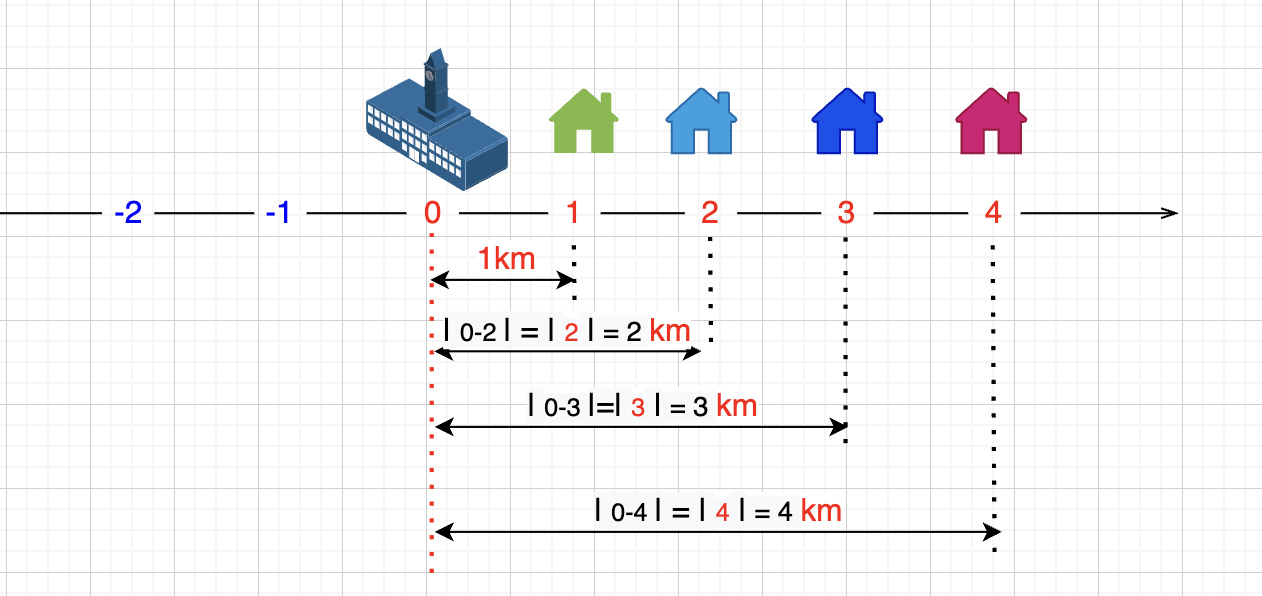
这个学校建的也不好,每位同学都要走 0-1 这段路,那我试试将学校挪一下,挪到 1 位置上试试,即 x=1 时,总距离 = |1-1|+|1-2|+|1-3|+|1-4| = 0+1+2+3 = 6 km
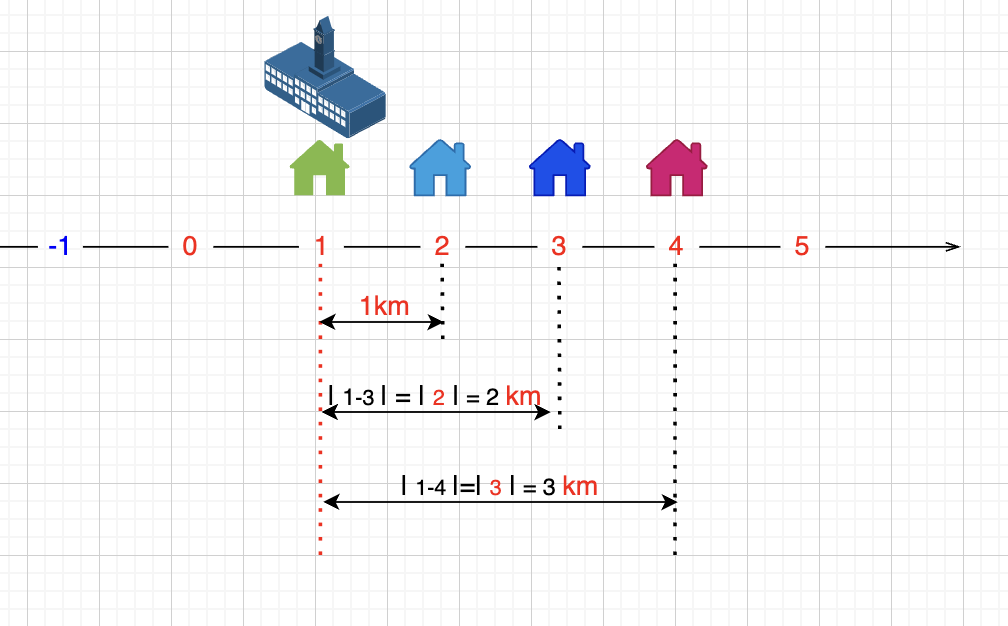
看见没有,仅仅是挪动了一下,马上减少了4公里,有位同学甚至住到了学校旁边,连走路都不用走了!我们还可以继续挪到 2,3,4 位置上
我们列个表看一下 x 分别从 -1~6 取值时,总距离 |x-1|+|x-2|+|x-3|+|x-4|的变化
| x | -1 | 0 | 1 | 2 | 2.5 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|
| |x-1|+|x-2|+|x-3|+|x-4| | 14 | 10 | 6 | 4 | 4 | 4 | 6 | 10 | 14 |
其中,x 在 2~3 之间取任意值,计算的总距离都是4,而且是最小的,不信你可以代入验算一下,这是有理可证的,下面我们会解释这个奇特的现象的
回归正题
现在我们再回过头来 看这个问题,求 |x-1|+|x-2|+|x-3|+...|x-n| 在什么时候取最小值,看看我们上面建学校问题,和计算总距离是不是一模一样!
这道题就相当于是:在 1,2,3,4,...,n 点上都住了一位同学,我要去选一个好地方来建一个好学校(假设建在x点),要让所有同学总距离最小,也就是尽可能让全部同学路线少重合
我们抛开数学绝对值式子,单纯让你来建学校,你会把学校选址在哪里?
直觉告诉我们,学校建在中心区最好,同学都在学校附近,事实也确实是这样,我们再来推理一下,大家可以拿出纸和笔分别画一下
- 如果有2个点,例如 1,2 住着2个同学,那学校建在中间的1~2点之间任何位置都可以,最小总距离总是 1km = 2-1,即数轴上
2到1 的距离,见图1 - 如果有3个点,例如 1,2,3 住着3个同学,那学校建在中间的点 2,最小总距离就是 2km = 3-1,即
3到1 之间的距离,见图2 - 如果有4个点,例如 1,2,3,4 住着4个同学,那学校建在中间的 2~3 点之间任何位置都可以,最小总距离就是 4km = 3-2 + 4-1,即
3到2的距离 + 4到1的距离,见图3 - 如果有5个点,例如 1,2,3,4,5 住着5个同学,那学校建在中间的点 3,最小总距离就是 6km = 4-2 + 5-1,即
4到2的距离 + 5到1的距离 - 如果有6个点,例如 1,2,3,4,5,6 住着6个同学,那学校建在中间的点 3~4 点之间任何位置都可以,最小总距离就是 9km = 4-3 + 5-2 + 6-1,即
4到3 + 5到2 + 6到1的距离
...
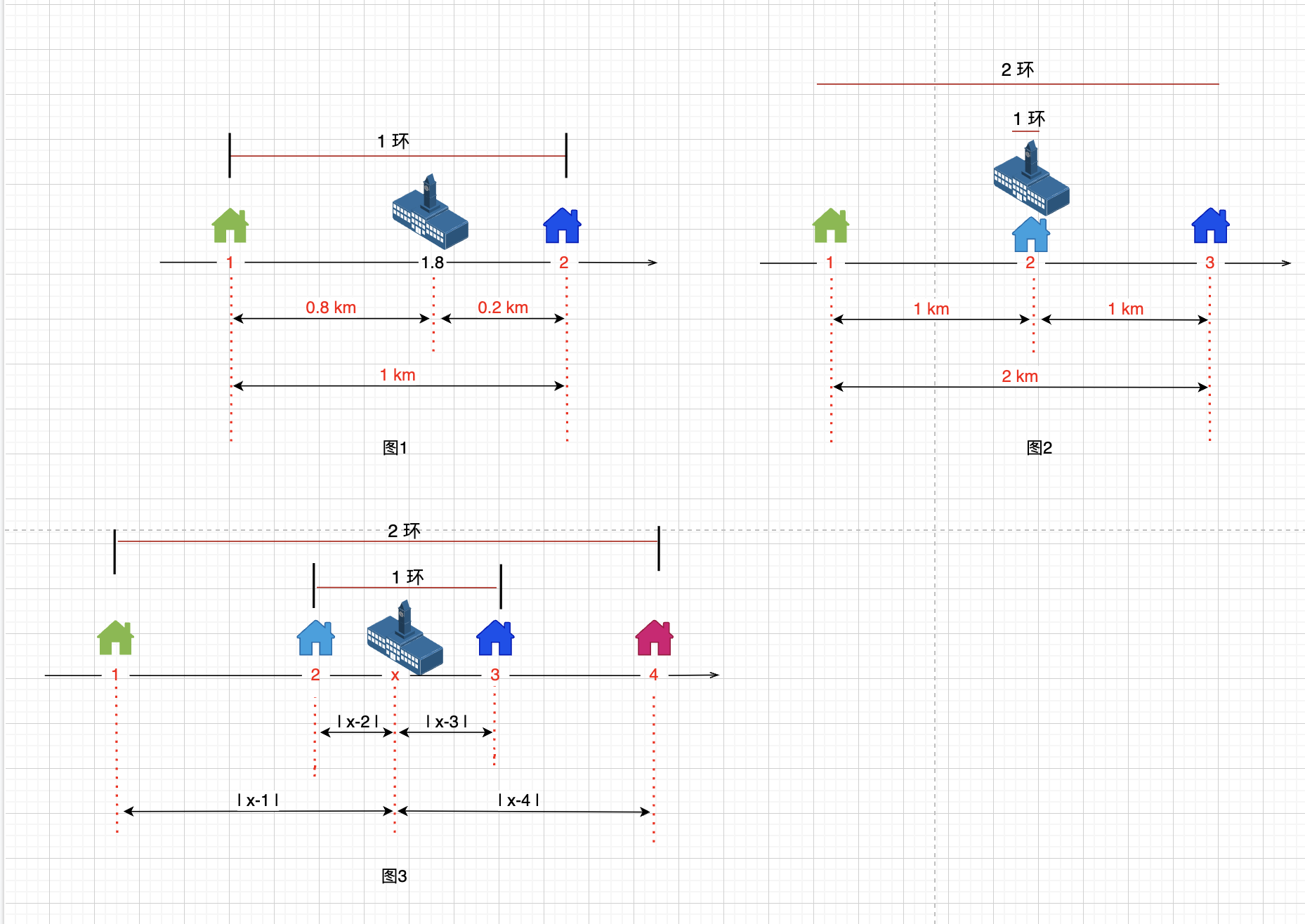
是不是很奇妙?2-1 居然可以看成 2到1之间的距离,3-2 为 3到2的距离,...
因为,相差就是绝对值,绝对值就是距离,那么,绝对值|3 -(-5)|,我们完全可以说是求数轴上 3 到 -5 两点间的距离,那就是8啊,是不是超简单!
我们从上面的规律归纳出这样的结果:
1.如果有奇数个点住着同学们,学校就建在 (1+n)/2 的地方,即 x = (1+n)/2
2.如果有偶数个点住着同学们,学校就建在 (n/2)~(n/2)+1 之间的任意地方,即 x 在(n/2)和(n/2)+1 之间取任意值都可以
总距离最小值
我们甚至还能算出总距离 |x-1|+|x-2|+|x-3|+...|x-n| 的最小值,就是以学校为中心,最近的一环的两点距离 + 二环两点距离 + 三环两点的距离 + ... + 最远的那环距离
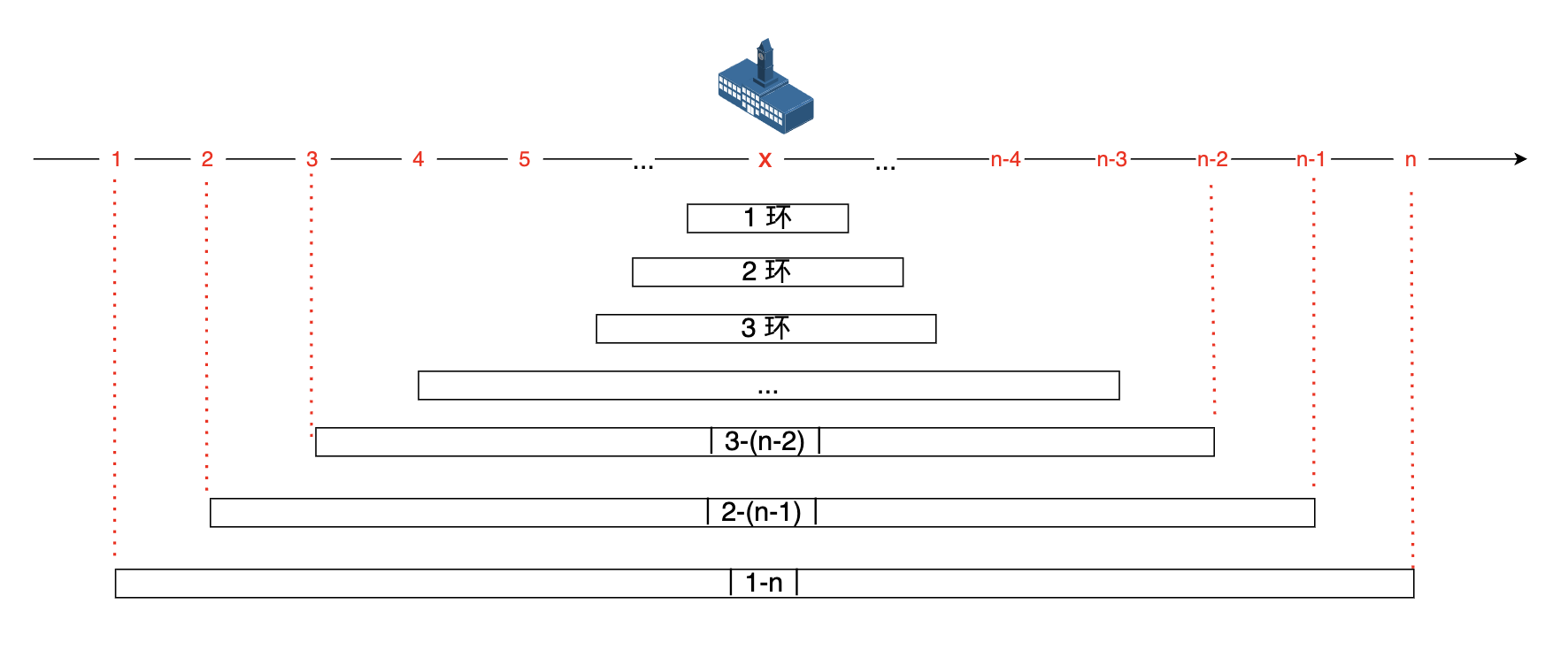
举例:
在 1,2,3,4,5 住着5个同学为例,一环的点就只有一个3,二环是2和4,三环是1和5
在 1,2,3,4,5,6 住着6个同学为例,一环的两点就是3和4,二环是2和5,三环是1和6
|x-1|+|x-2|+|x-3|+...|x-n| = n-1 + (n-1)-2 + (n-2)-3 + ... = 最外环n到1的距离 + (n-1)到2点的距离 + (n-2)到3点的距离 + ... + 最内的一环距离
-
当 n 为偶数时,
总距离 = n-1 + n-3 + n-5 + n-7 + n-9 + ... + 7 + 5 + 3 + 1,各项全是奇数,总共有 n/2 项,利用等差数列公式 (首项+末项)*项数/2 求得
总距离 = ( ( ( n − 1 ) + 1 ) ∗ n 2 ) ∗ 1 2 = n 2 4 总距离 = (((n-1) + 1) * \frac{n}{2})* \frac{1}{2} = \frac{n^2}{4} 总距离=(((n−1)+1)∗2n)∗21=4n2
用 n=2 代入,得 总距离 = 1,用 n=4 代入,得 总距离 = 4
-
当 n 为奇数时,
总距离 = n-1 + n-3 + n-5 + n-7 + n-9 + ... + 6 + 4 + 2 + 0,各项全是偶数,总共有 (n+1)/2 项利用等差数列公式 (首项+末项)*项数/2 求得
总距离 = ( ( ( n − 1 ) + 0 ) ∗ n + 1 2 ) ∗ 1 2 = n 2 − 1 4 总距离 = (((n-1) + 0) * \frac{n+1}{2})* \frac{1}{2} = \frac{n^2-1}{4} 总距离=(((n−1)+0)∗2n+1)∗21=4n2−1
用 n=3 代入,得 总距离 = 2,用 n=5 代入,得 总距离 = 6,与上面我们推理一下的结果完全一致!
总结
总结一下,主要思想有下面两点:
- 绝对值就是距离,距离就是绝对值
- 绝对值 |x-n| 可以看作数轴上 x 点到 n 点的距离