【算法】分治

1、快速排序

1.1基本思想

快速排序是 Hoare 于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该基准值将待排序集合分割成两子序列,左子序列中所有元素均小于或等于 基准值,右子序列中所有元素均大于或等于 基准值,**如果以基准值成功将区间中的数据进行划分，那么这个基准值就已经放在了它排好序后应出现的位置。这是快速排序最核心的步骤。**然后对左右子序列（前提是左右序列存在，并且长度大于1）重复该过程,直到所有元素都排列在相应位置上为止。

cpp 复制代码

// 假设按照升序对array数组中[left,right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
    if(right - left <= 1)
    return;

    // 按照基准值对array数组的 [left, right)区间中的元素进行划分
    int div = partion(array, left, right);
    // 划分成功后以div为边界形成了左右两部分 [left, div)和 [div+1, right) 
    
    // 递归排[left, div) 
    QuickSort(array, left, div);

    // 递归排[div+1, right) 
    QuickSort(array, div+1, right);
}

上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,写递归框架时可想想二叉树前序遍历规则即可快速写出来,后续只需分析如何按照基准值来对区间中数据进行划分的方式即可。

1.2快排的单趟排序

采用"数组分三块"的思想，根据随机选取的基准值，将数组从左到右分为小于基准值的、等于基准值、大于基准值的三部分。用 left 指针指示小于基准值的部分的右端点，用 right 指针指示大于基准值的部分的左端点，用 i 指针来遍历序列，如图所示：

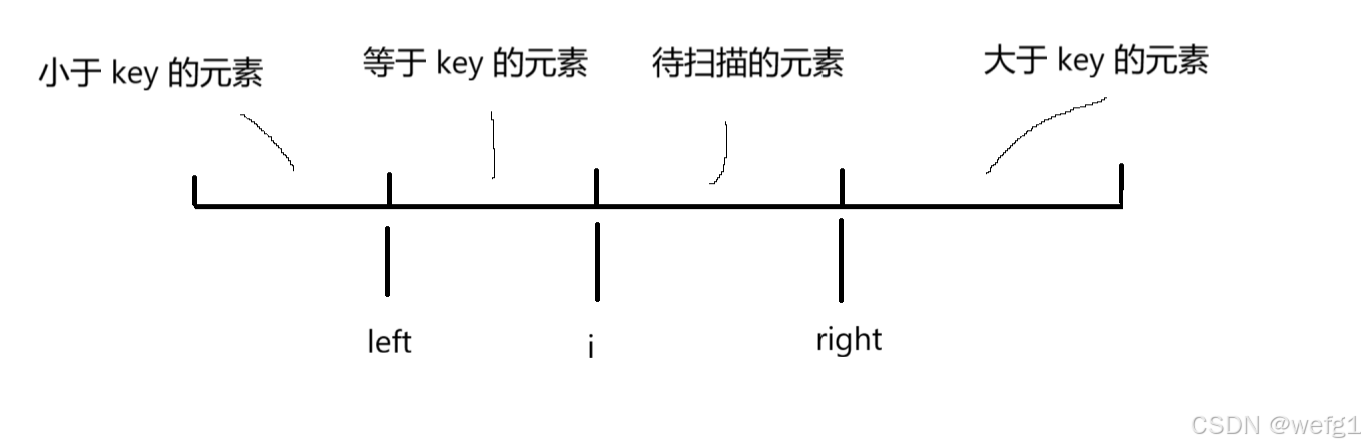
当 i 所指示的元素小于 key 时，就将该元素与 left 位置的下一个元素交换，当 i 所指示的元素大于 key 时，就将该元素与 right 位置的上一个元素交换，当 i 所指示的元素等于 key 时，i++。循环继续的条件就是 i < right, 当 i == right 时，数组已经被分成小于基准值的、等于基准值、大于基准值的三部分。

1.3快排的递归实现

将数组从左到右分为小于基准值的、等于基准值、大于基准值的三部分后，只需对小于基准值的部分和大于基准值的部分再进行"数组分三块"，直到数组不存在，或数组只有一个元素。

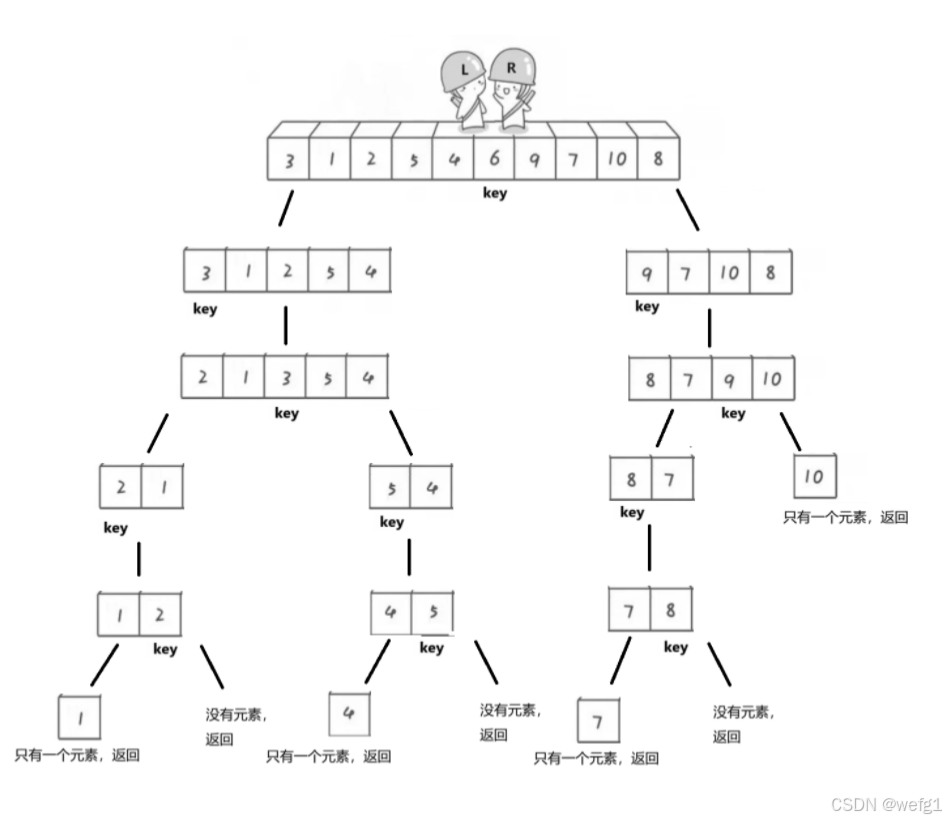
代码实现：

cpp 复制代码

void QuickSort(int* a, int l, int r)
{
    if (l >= r) return; // 数组不存在或只有一个元素，返回

    int key = GetRandom(a,l,r); 在 l 到 r 随机选择一个数作为 key

    int left = l - 1,right = r + 1,i = l; // 注意 left 和 right 的初始位置
    
    while (i < right) // 注意不是 i < r
    {
        if(a[i] < key) swap(a[++left],a[i++]);
        else if(a[i] > key) awap(a[--right],a[i]);
        
        // 细节：将 a[i] 和 right 的上一个位置的值交换后，i 不能向后移动
        // 因为 right 的上一个位置的值是待扫描的元素，交换后 i 位置要判断与 key 的关系
        
        else i++; // a[i] == key 时
    }
    
    // [l, left] [left+1,right-1] [right, r] 
    // 递归
    
    QuickSort(a, l, left); 
    QuickSort(a, right, r);
}

int GetRandom(int* a,int l,int r)
{
    // 在主函数种随机数种子
    // srand(time(NULL));
    return a[rand() % ( r - l + 1 ) + l]
}

1.4例题

题目链接

cpp 复制代码

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int i = 0;
        int left = -1;
        int right = nums.size();

        while(i < right)
        {
            if(nums[i] == 0) swap(nums[++left],nums[i++]);
            else if(nums[i] == 1) i++;
            else if(nums[i] == 2) swap(nums[--right],nums[i]);
        }
    }
};

题目链接

解析：采用"数组分三块"的方法处理数组后，比较 k 与数组三个部分的长度：假设大于 key 的部分的长度是 b，等于 key 的部分的长度是 c，如果 k <= b，那么只需要递归大于 key 的部分，找大于 key 的部分的第 k 大即可，如果 k <= b 不成立，而 k <= b + c 成立，此时直接返回 key，如果都不成立，递归小于 key 的部分，找小于 key 的部分的第 k - b - c 大。如果递归的数组长度为 1，直接返回。

cpp 复制代码

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        
        srand(time(NULL));
        return rfindKthLargest(nums,0,nums.size() - 1,k);
    }

    int rfindKthLargest(vector<int>& nums,int l,int r,int k)
    {
        if(l == r) return nums[l];
        int key = GetRandom(nums,l,r);

        int left = l - 1,right = r + 1,i = l;
        while(i < right)
        {
            if(nums[i] < key) swap(nums[++left],nums[i++]);
            else if(nums[i] == key) i++;
            else swap(nums[--right],nums[i]);
        }

        if(r - right + 1 >= k) return rfindKthLargest(nums,right,r,k);
        else if(r - left >= k) return key;
        else return rfindKthLargest(nums,l,left,k - r + left);
    }

    int GetRandom(vector<int>& nums,int l,int r)
    {
        return nums[rand() % (r - l + 1) + l];
    }
};

题目链接

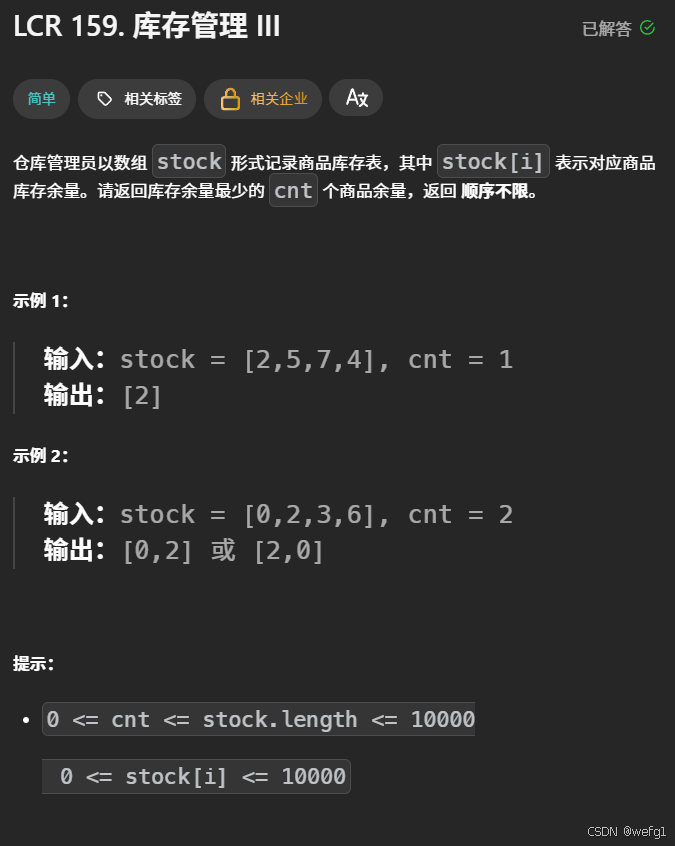
cpp 复制代码

class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) {
        srand(time(NULL));
        
        rinventoryManagement(stock,0,stock.size() - 1,cnt);

        return {stock.begin(),stock.begin()+cnt};
    }

    void rinventoryManagement(vector<int>& stock,int l,int r,int cnt)
    {
        if(cnt == 0) return;
        if(l >= r) return;
        int key = GetRandom(stock,l,r);
        int left = l - 1,right = r + 1,i = l;

        while(i < right)
        {
            if(stock[i] < key) swap(stock[++left],stock[i++]);
            else if(stock[i] > key) swap(stock[--right],stock[i]);
            else i++;
        }

        int a = left - l + 1, b = right - l;
        if(cnt < a) rinventoryManagement(stock,l,left,cnt);
        else if (cnt <= b) return;
        else rinventoryManagement(stock,right,r,cnt - b);
    }

    int GetRandom(vector<int>& stock,int l,int r)
    {
        return stock[rand() % (r - l + 1) + l];
    }
};

2、归并排序

2.1基本思想

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。归并排序核心步骤:

归并排序可以看成二叉树的后序遍历，该"二叉树"的根的作用是分解与合并，即分解出"左子树"和"右子树"，先把"左子树"排好序，再把"右子树"排好序，当"左子树"和"右子树"都是有序的前提下，再和并"左子树"和"右子树"，合并好后"左子树"和"右子树"所表示的数组区间已经有序，再把该数组区间返回给上层递归，该数组区间可能是上层递归的"左子树"或"右子树"。

2.2代码实现

要创建一个临时数组，来存储合并后的结果，再将临时数组的内容拷贝到原数组

cpp 复制代码

void MergeSort(int* a, int n)
{
    int* tmp = (int*)malloc(sizeof(int) * n); 
    if (tmp == NULL)
    {
        perror("malloc fail\n");
        return;
    }
    
    _MergeSort(a, 0, n - 1, tmp);
    
    free(tmp);
}

为了实现递归，MergeSort 函数不能调用自己，不然每次递归都要创建数组。所以我们新命名一个函数 _MergeSort ，在这个函数中实现递归。

cpp 复制代码

void _MergeSort(int* a, int begin, int end, int* tmp)
{
    if(begin >= end)
        reurn;

    int mid = (begin + end) / 2; 
    
    // [begin, mid] [mid+1,end], 子区间递归排序
    _MergeSort(a, begin, mid, tmp); 
    _MergeSort(a, mid+1, end, tmp);

    // [begin, mid] [mid+1,end]归并
    int begin1 = begin, end1 = mid; 
    int begin2 = mid+1, end2 = end; 
    int i = begin; 

    while (begin1 <= end1 && begin2 <= end2)
    {
        if (a[begin1] <= a[begin2])
        {
            tmp[i++] = a[begin1++];
        }
        else
        {
            tmp[i++] = a[begin2++];
        }
    }

    while (begin1 <= end1)
    {
        tmp[i++] = a[begin1++]
    }

    while (begin2 <= end2)
    {
        tmp[i++] = a[begin2++];
    }

    memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

代码注意点：

1、while 循环的条件是循环继续的条件而不是循环结束的条件，所以 while (begin1 <= end1 && begin2 <= end2) 中 && 不能写成 || 。只要有一个子区间全部归并到了 tmp ，就结束循环，由下面的代码判断是哪个子区间还有元素没有归并。

2、归并时如果两个数相等，就把 a[begin1] 放在 tmp 数组，这样可以保证稳定性。

3、归并一次后就立刻将 tmp 对应区间复制给原数组，而不能将所有子数组都归并完后再一把将 tmp 复制给原数组，因为归并的操作必须保证两个子数组都是有序的

tmp 数组建议定义成全局数组，这样每次拷贝就不用临时创建数组了，效率会更快一点。

2.3例题

题目链接

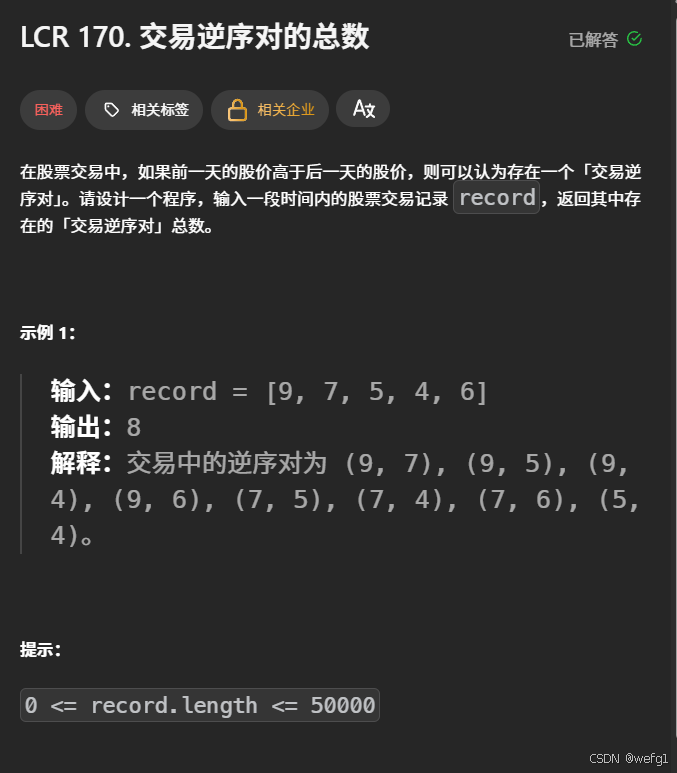
解析：在归并排序即将合并左右两个子区间之前，根据左右两个子区间都是升序，通过一次比较快速统计出多种情况：当左区间某数大于右区间某数时，右区间内所有小于左区间该数的数值都能与之构成逆序对，逆序对的数量等于右区间该数左侧元素的个数。

cpp 复制代码

class Solution {
public:
    int reversePairs(vector<int>& record) {
        vector<int> tmp;
        tmp.resize(record.size());
        int count = 0;
        _MergeSort(record,0,record.size() - 1,tmp,count);
        return count;
    }

    void _MergeSort(vector<int>& a, int begin, int end, vector<int>& tmp,int& count)
    {
        if(begin >= end) return;

        int mid = (begin + end) / 2; 
        
        // [begin, mid] [mid+1,end], 子区间递归排序
        _MergeSort(a, begin, mid, tmp,count); 
        _MergeSort(a, mid+1, end, tmp,count);

        int b1 = begin, e1 = mid; 
        int b2 = mid+1, e2 = end; 
        
        while(e1 >= b1 && e2 >= b2)
        {
            if(a[e1] > a[e2]) 
            {
                count += e2 - b2 + 1;
                e1--;
            }
            else e2--;
        }

        int begin1 = begin, end1 = mid; 
        int begin2 = mid+1, end2 = end; 
        int i = begin; 

        while (begin1 <= end1 && begin2 <= end2)
        {
            if (a[begin1] <= a[begin2]) tmp[i++] = a[begin1++];
            else tmp[i++] = a[begin2++];
        }

        while (begin1 <= end1) tmp[i++] = a[begin1++];
        while (begin2 <= end2) tmp[i++] = a[begin2++];

        for(int i = begin; i <= end; i++) a[i] = tmp[i];
    }

};