Hot100-哈希，双指针

1.两数之和

思路

1. 创建一个无序哈希表unordered_map<int, int>，用于存储数组元素的值和对应的索引
2. 遍历数组nums中的每个元素：
   • 计算目标值与当前元素的差值aim = target - nums[i]
   • 检查哈希表中是否存在这个差值：
     • 如果存在，说明已经找到一对符合条件的元素，返回它们的索引
     • 如果不存在，将当前元素的值和索引存入哈希表
3. 如果遍历结束仍未找到，返回空向量

代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> um;
        for(int i=0;i<nums.size();i++)
        {
            int aim=target-nums[i];
            if(um.count(aim))
            {
                vector<int> ret;
                ret.push_back(um[aim]);
                ret.push_back(i);
                return ret;
            }

            um[nums[i]]=i;
        }
        vector<int> ret;
        return ret;
    }
};

49.字母异位词分组

思路

1. 创建一个无序哈希表unordered_map<string, vector<string>>，用于将排序后的字符串作为键，字母异位词集合作为值
2. 遍历输入的字符串数组strs：
   • 对每个字符串创建一个临时副本tmp
   • 对临时副本进行排序（排序后，所有字母异位词会拥有相同的排序结果）
   • 将原字符串添加到哈希表中对应排序后字符串的向量里
3. 遍历哈希表，将每个键对应的向量（即一组字母异位词）添加到结果向量中
4. 返回最终的结果向量

这种方法的核心思路是：字母异位词经过排序后会得到相同的字符串，利用这一特性作为哈希表的键，就能高效地将所有字母异位词分组。

代码

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string,vector<string>> um;
        for(int i=0;i<strs.size();i++)
        {
            string tmp=strs[i];
            sort(tmp.begin(),tmp.end());
            um[tmp].push_back(strs[i]);
        }

        vector<vector<string>> ret;
        for(auto &t:um)
        {
            ret.push_back(t.second);
        }

        return ret;
    }
};

128最长连续序列

思路

1. 首先将所有数字存入无序集合unordered_set<int>中：

   • 利用集合的特性实现 O (1) 时间复杂度的查找
   • 自动去除重复元素，不影响连续序列的计算

2. 初始化最长连续序列长度longestStreak为 0

3. 遍历集合中的每个数字：

   • 对于每个数字，先检查它是否是一个连续序列的起点（即num - 1不在集合中）
   • 如果是起点，则开始向后查找连续数字：
     • 初始化当前数字currentNum为起点数字
     • 初始化当前连续序列长度currentStreak为 1
     • 循环检查currentNum + 1是否在集合中，若存在则继续向后查找并增加序列长度
   • 更新最长连续序列长度

4. 返回最长连续序列长度

代码

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set;
        for (const int& num : nums) {
            num_set.insert(num);
        }

        int longestStreak = 0;

        for (const int& num : num_set) {
            if (!num_set.count(num - 1)) {
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.count(currentNum + 1)) {
                    currentNum += 1;
                    currentStreak += 1;
                }

                longestStreak = max(longestStreak, currentStreak);
            }
        }

        return longestStreak;           
    }
};

283移动零

思路

1. 初始化两个指针left和right，都从 0 开始
2. 使用right指针遍历整个数组：
   • 当right指向的元素是非零值时：
     • 交换left和right指针指向的元素
     • 将left指针向右移动一位
   • 无论是否交换，right指针始终向右移动一位
3. 遍历结束后，所有非零元素都被移动到了数组前部，且保持了原有的相对顺序，零元素则全部移到了数组末尾

这种方法的优势是：

• 只需要一次遍历即可完成操作
• 不需要额外的辅助数组，空间复杂度为 O (1)
• 非零元素的相对顺序得到了保留

代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int n = nums.size(), left = 0, right = 0;
        while (right < n) {
            if (nums[right]) {
                swap(nums[left], nums[right]);
                left++;
            }
            right++;
        }
    }
};

11.盛水最多的容器

思路

1. 初始化两个指针，l（左指针）指向数组起始位置，r（右指针）指向数组末尾
2. 初始化最大面积ans为 0
3. 使用双指针遍历数组，直到左指针超过右指针：
   • 计算当前指针所指的两条线段形成的容器面积：宽度为r-l，高度为两条线段中的较短线段高度min(height[r], height[l])
   • 更新最大面积ans（取当前面积和历史最大面积中的较大值）
   • 移动指针：
     • 如果左指针的线段高度小于或等于右指针的，移动左指针向右（l++）
     • 否则，移动右指针向左（r--）
4. 返回最大面积ans

这种方法的核心思路是：容器的面积由宽度和高度共同决定，宽度随指针移动而减小，所以要寻找更高的线段来可能获得更大面积。通过移动较短线段的指针，才有可能找到更大的面积，这是一种贪心策略的应用。

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l=0,r=height.size()-1;
        int ans=0;
        while(l<r)
        {
            ans=max(ans,(r-l)*min(height[r],height[l]));
            if(height[l]<=height[r])
            {
                l++;
            }
            else 
            {
                r--;
            }
            
        }

        return ans;
    }
};

15.三数之和

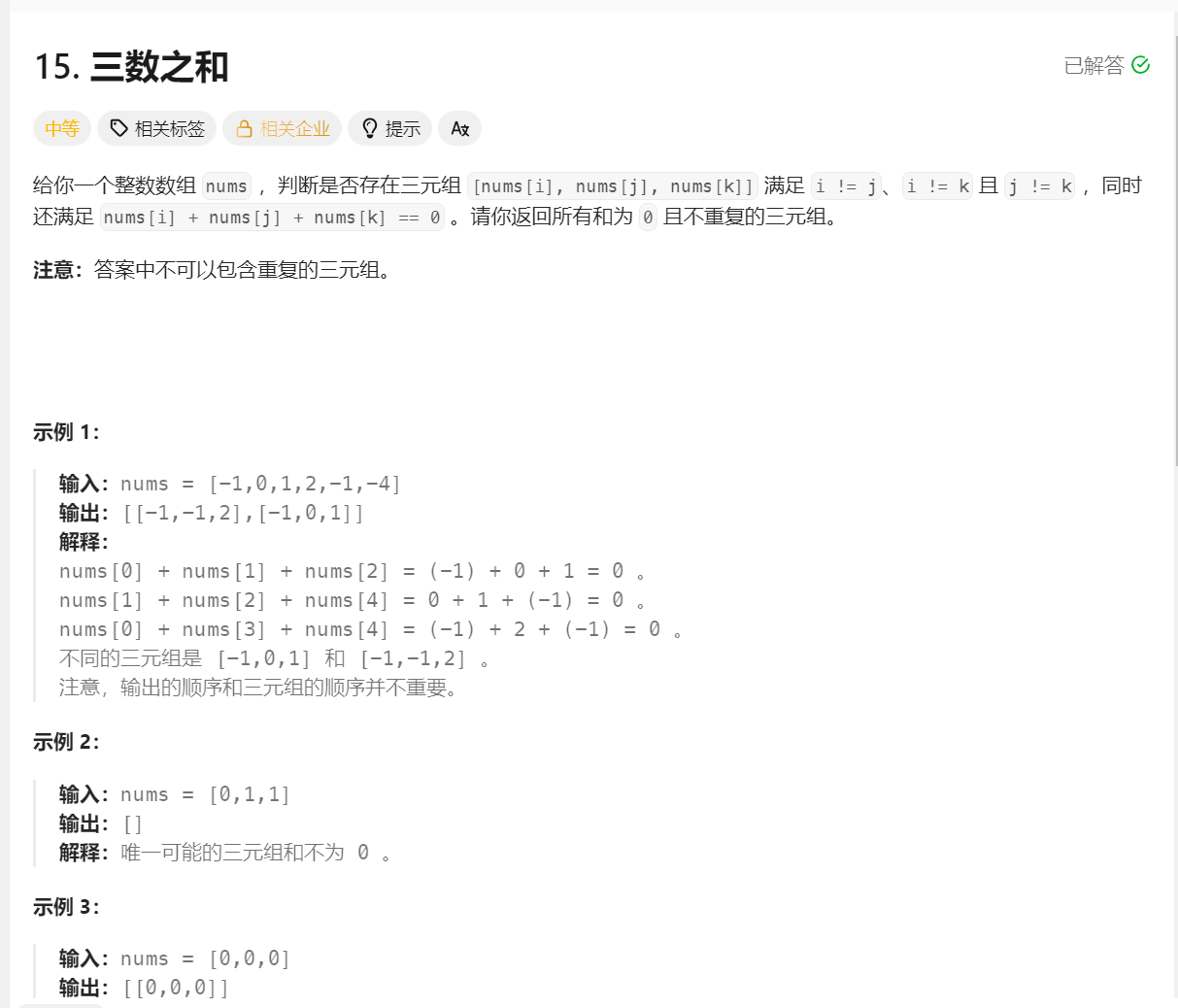
思路

1. 首先对数组进行排序：

   • 排序有助于后续的去重操作
   • 便于使用双指针寻找符合条件的元素组合

2. 外层循环枚举第一个元素a（索引为first）：

   • 跳过与前一个元素相同的值，避免重复结果
   • 计算目标值target = -a，即需要找到的另外两个元素之和

3. 内层使用双指针寻找另外两个元素b和c：

   • second指针从first + 1开始（作为b的索引）
   • third指针从数组末尾开始（作为c的索引）
   • 同样跳过b的重复值
   • 调整third指针位置，使b + c尽可能接近target：
     • 若b + c > target，则左移third指针
     • 若b + c == target，则找到一组解，加入结果集
     • 若second与third指针相遇，则退出内层循环

4. 返回所有符合条件的三元组

这种方法的核心优势是：

• 通过排序和跳过重复元素，有效避免了结果集中出现重复的三元组
• 使用双指针将原本 O (n³) 的暴力解法优化为 O (n²)，大幅提升效率

代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<vector<int>> ans;
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    ans.push_back({nums[first], nums[second], nums[third]});
                }
            }
        }
        return ans;
    }
};

42接雨水

思路

1. 初始化两个指针l（左指针）和r（右指针），分别指向数组的首尾
2. 初始化两个变量lmax和rmax，分别记录左侧和右侧的最大高度，初始值为 0
3. 初始化结果变量ans用于累计接水量，初始值为 0
4. 当左指针小于等于右指针时，循环执行：
   • 若左侧当前高度处高度小于等于右侧侧：
     • 更新左侧最大高度lmax（取当前lmax和h[l]中的较大值）
     • 计算当前位置可接的雨水量（lmax - h[l]），累加到ans
     • 左指针右移（l++）
   • 否则（右侧高度较小）：
     • 更新右侧最大高度rmax（取当前rmax和h[r]中的较大值）
     • 计算当前位置可接的雨水量（rmax - h[r]），累加到ans
     • 右指针左移（r--）
5. 返回累计的接水量ans

这种方法的核心思路是：每个位置能接的雨水量取决于它左右两侧的最大高度中的较小值与自身高度的差值。通过双指针从两端向中间移动，始终处理较矮一侧的柱子，因为较矮一侧的最大高度是确定的（由另一侧的更高柱子限制）。

代码

class Solution {
public:
    int trap(vector<int>& h) {
        int l=0,r=h.size()-1;
        int lmax=0,rmax=0;
        int ans=0;
        while(l<=r)
        {
            if(h[l]<=h[r])
            {
                lmax=max(lmax,h[l]);
                ans+=lmax-h[l];
                l++;
            }
            else 
            {
                rmax=max(rmax,h[r]);
                ans+=rmax-h[r];
                r--;
            }
        }

        return ans;
    }
};