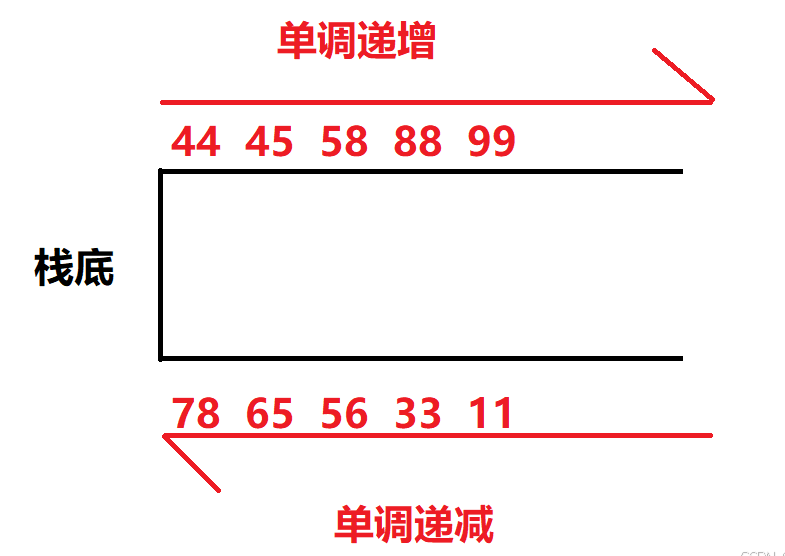
单调栈(Monotonic Stack)是一种特殊的栈结构,其内部元素始终保持单调递增 或单调递减 的顺序。它在算法设计中非常有用,尤其适用于解决与"最近更大/更小元素"相关的问题。
一、核心思想
-
维护栈的单调性:每次入栈前,若新元素会破坏单调性,则弹出栈顶元素,直到满足单调条件。
-
利用这种性质,可以在 O(n) 时间内解决某些需要比较"前后关系"的问题。
-
具体代码实现:
cpp#include <vector> #include <stack> using namespace std; int main() { vector<int> v = {2, 1, 5, 6, 2, 3}; stack<int> st; // 存储下标,让st栈中元素是单调递增的(对应值) // /当前元素往左边第一个小于它的元素下标,初始化为 -1 vector<int> index(v.size()); for (int i = 0; i < v.size(); i++) { // 弹出所有大于等于 v[i] 的元素(因为它们不可能成为后续元素的"左边更小") while (!st.empty() && v[st.top()] >= v[i]) { st.pop(); } // 如果栈空,为-1. 非空栈顶就是左边第一个小于 v[i] 的下标 index[i] = st.empty() ? -1 : st.top(); st.push(i); // 压入当前下标 } // 输出 index for (int x : index) { cout << x << " "; } // 输出: -1 -1 1 2 1 4 } /* i: 0 1 2 3 4 5 v: 2 1 5 6 2 3 index: -1 -1 1 2 1 4 */
二、常见用途
1. 寻找每个元素左边/右边第一个更大(或更小)的元素
- 典型题目 :
- 下一个更大元素(Next Greater Element)
- 每日温度(LeetCode 739)
- 应用:用于快速构建"下一个更大值"数组。
2. 计算最大矩形面积(直方图中最大矩形)
- 题目:LeetCode 84. Largest Rectangle in Histogram
- 原理:利用单调递增栈,当遇到比栈顶小的柱子时,说明以栈顶高度为高的矩形不能再向右扩展,此时计算面积。
3. 滑动窗口最大值/最小值(配合双端队列更常见,但思想类似)
- 虽然通常用单调队列实现,但思想源自单调栈。
4. 接雨水(Trapping Rain Water)
- 题目:LeetCode 42
- 方法之一:使用单调递减栈,记录可能形成"凹槽"的位置,当遇到更高的柱子时,计算可接雨水量。
5. 移掉 K 位数字使剩余数字最小
- 题目:LeetCode 402. Remove K Digits
- 策略:维护一个单调递增栈,若当前数字小于栈顶且还能删除(k > 0),则弹出栈顶。
6. 股票价格跨度(Stock Span)
- 题目:LeetCode 901
- 做法:用单调递减栈存储(价格, 天数),快速计算连续小于等于当前价格的天数。
三、优势
- 时间复杂度低 :每个元素最多入栈和出栈一次 → O(n)
- 空间换时间:用栈记录潜在候选,避免重复比较
- 总结口诀:"找最近更大用递减栈,找最近更小用递增栈;破坏单调就弹出,顺势更新答案好。"
四、实战
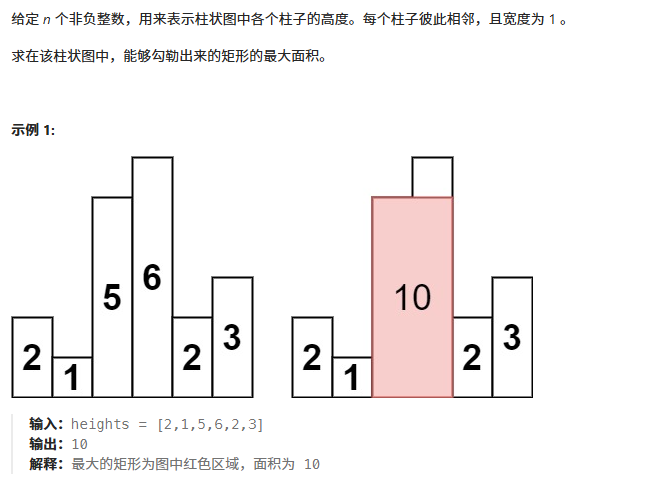
例题一:84. 柱状图中最大的矩形
解题思路:
使用单调递增栈来存储。当不满足时,说明右边的已经无法拼接出更大的面积。那么我们就一边出栈,一边计算最大面积。
特例:如果单调栈中是位于栈底,说明该元素是最小元素,也就是让它的下标为-1,最后在计算的时候,就是计算sz的宽度了。
代码实现:
cpp
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<pair<int,int>> s; //第一个参数为值,第二个为下标
int sz = heights.size();
int Max=0;
for(int i=0;i<sz;i++){
while(!s.empty() && s.top().first>heights[i]){
auto temp = s.top();
s.pop();
//需要在出栈的时候就计算,因为面积和宽高都有关。
//不能先统计出左边第一个小于的下标,不能只计算一次。
int left_bound = s.empty() ? -1 : s.top().second;
int temp_max = temp.first * (i - left_bound -1);
Max = max(Max,temp_max);
}
s.push({heights[i],i});
}
while(!s.empty())
{
auto temp = s.top();
s.pop();
int left_bound = s.empty() ? -1 : s.top().second;
int temp_max = temp.first * (sz - left_bound -1);
Max = max(Max,temp_max);
}
return Max;
}
};四、复杂度:
时间复杂度:O(n) --- 每个元素最多入栈和出栈一次
空间复杂度:O(n) --- 最坏情况下(例如输入数组单调递增),所有元素都会被压入栈中
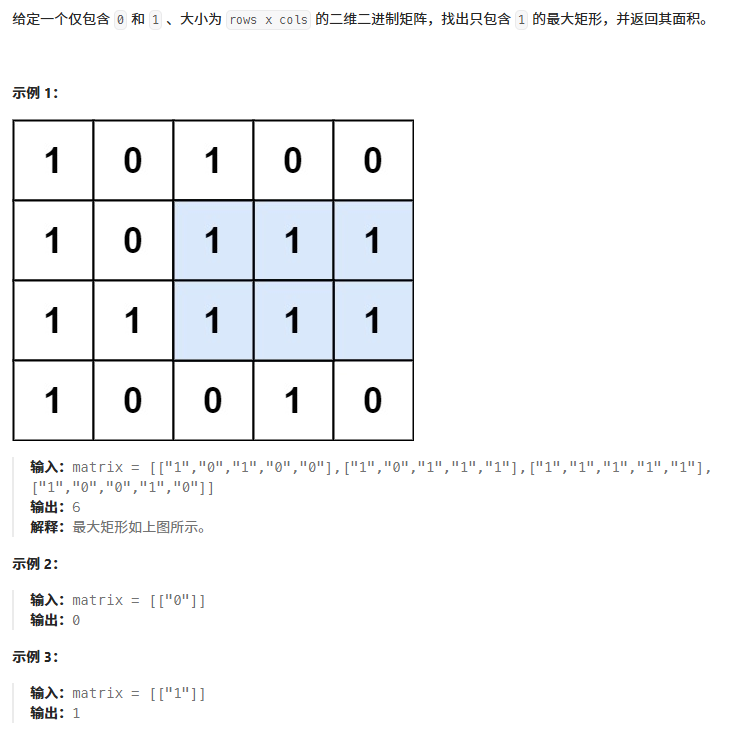
例题二:85. 最大矩形
解题思路:
以第一行为底的柱子高度为 [1,0,1,0,0],最大矩形面积为 1。
以第二行为底的柱子高度为 [2,0,2,1,1],最大矩形面积为 3。
以第三行为底的柱子高度为 [3,1,3,2,2],最大矩形面积为 6。
以第四行为底的柱子高度为 [4,0,0,3,0],最大矩形面积为 4。
答案为 max(1,3,6,4)=6。
由于我们枚举的是矩形的底边,如果 matrix[i][j]=0,那么没有柱子,高度等于 0。否则,在上一行柱子的基础上,把柱子高度增加 1。形象地说,就是在柱子下面要有"地基"。
C++代码实现:
cpp
class Solution {
private:
//获取一行的最大矩形
int largestRectangleArea(vector<int>& heights) {
stack<pair<int,int>> s; //第一个参数为值,第二个为下标
int sz = heights.size();
int Max=0;
for(int i=0;i<sz;i++){
while(!s.empty() && s.top().first>heights[i]){
auto temp = s.top();
s.pop();
int left_bound = s.empty() ? -1 : s.top().second;
int temp_max = temp.first * (i - left_bound -1);
Max = max(Max,temp_max);
}
s.push({heights[i],i});
}
while(!s.empty())
{
auto temp = s.top();
s.pop();
int left_bound = s.empty() ? -1 : s.top().second;
int temp_max = temp.first * (sz - left_bound -1);
Max = max(Max,temp_max);
}
return Max;
}
public:
int maximalRectangle(vector<vector<char>>& matrix) {
vector<vector<int>> int_matrix(matrix.size(),vector<int>(matrix[0].size()));
for(int i=0;i<matrix.size();i++)
{
for(int j=0;j<matrix[0].size();j++)
{
if(matrix[i][j]=='0') int_matrix[i][j] = 0;
else int_matrix[i][j] = 1;
}
}
int Max = 0;
for(int i=0;i<matrix.size();i++)
{
if(i!=0) //动态规划
{
for(int j=0;j<int_matrix[i].size();j++)
{
if(int_matrix[i][j]!=0) int_matrix[i][j] += int_matrix[i-1][j];
//如果为0,就还是0,没有"地基"
}
}
int temp_max = largestRectangleArea(int_matrix[i]);
Max = max(Max,temp_max);
}
return Max;
}
};复杂度:
- 时间复杂度:O(mn),其中 m 和 n 分别为 matrix 的行数和列数。做 m 次 84 题,每次 O(n)。
- 空间复杂度:O(n)。