d ≡ e⁻¹ mod φ(n)(e的模逆元)
等价于
e * d ≡ 1 mod φ(n)
私钥 d 的两个表达式关系详解
这两个表达式 完全等价,它们只是表示同一个数学概念的不同写法。
1. 两个表达式的含义
-
e * d ≡ 1 mod φ(n)
这是RSA私钥d的定义式:d是满足e乘以d在模φ(n)下等于1的整数。
-
d ≡ e⁻¹ mod φ(n)
这是e在模φ(n)下的乘法逆元的表示方式,其中e⁻¹表示e的模逆元。
2. 为什么它们等价?
在模运算中,如果a * b ≡ 1 mod m,那么b就是a在模m下的乘法逆元,记作b = a⁻¹ mod m。
所以:
- e * d ≡ 1 mod φ(n) ⇔ d = e⁻¹ mod φ(n)
这就像在普通算术中:
- 2 * 0.5 = 1 ⇔ 0.5 = 1/2
在模运算中,"除法"被表示为"乘以模逆元"。
3. 举例说明
假设:
- e = 7
- φ(n) = 10
那么:
- d = 3,因为 7 * 3 = 21 ≡ 1 mod 10
- 所以 d = e⁻¹ mod φ(n) = 7⁻¹ mod 10 = 3
因此:
- e * d ≡ 1 mod φ(n) ⇔ 7 * 3 ≡ 1 mod 10 ⇔ 21 ≡ 1 mod 10
- d ≡ e⁻¹ mod φ(n) ⇔ 3 ≡ 7⁻¹ mod 10
4. 在RSA中的应用
在RSA算法中:
- 公钥 = (e, n)
- 私钥 = (d, n)
其中d必须满足:d = e⁻¹ mod φ(n),即d是e在模φ(n)下的乘法逆元。
根据知识库[11]中的描述:"私钥d满足e * d ≡ 1 mod φ(n)(其中φ(n) = (p-1)(q-1))",这正是RSA加密和解密的核心数学原理。
5. 为什么需要这个关系?
在RSA中,加密过程是:c = m^e mod n 解密过程是:m = c^d mod n
要使这个过程成立,需要满足:m^(e*d) ≡ m mod n
通过欧拉定理,当e*d ≡ 1 mod φ(n)时,这个等式成立。这就是为什么d必须是e在模φ(n)下的乘法逆元。
总结
e * d ≡ 1 mod φ(n) 和 d ≡ e⁻¹ mod φ(n) 是完全等价的表达式,只是写法不同。在RSA算法中,d就是e在模φ(n)下的乘法逆元。
模逆元详解:RSA中的d ≡ e⁻¹ mod φ(n)
1. 模逆元的直观理解
模逆元就是"模运算中的倒数",就像普通数学中的倒数一样。
普通数学中的倒数:
- 3的倒数是1/3,因为3 × (1/3) = 1
- 5的倒数是1/5,因为5 × (1/5) = 1
模运算中的"倒数"(模逆元):
- 3在模10下的逆元是7,因为3 × 7 = 21,21 mod 10 = 1
- 7在模10下的逆元是3,因为7 × 3 = 21,21 mod 10 = 1
关键点:模逆元不是分数,而是一个整数,使得a × x ≡ 1 (mod m)。
2. RSA中的d ≡ e⁻¹ mod φ(n) 是什么意思
两种表达方式的等价性:
-
定义式:e × d ≡ 1 (mod φ(n))
- 这表示d是e在模φ(n)下的乘法逆元
-
表示式:d ≡ e⁻¹ (mod φ(n))
- 这是模逆元的标准表示方式,e⁻¹表示e的模逆元
它们完全等价,只是表达方式不同。
举例说明:
假设e = 7,φ(n) = 10
-
用定义式:e × d ≡ 1 (mod φ(n)) → 7 × d ≡ 1 (mod 10)
- 7 × 1 = 7 mod 10 = 7
- 7 × 2 = 14 mod 10 = 4
- 7 × 3 = 21 mod 10 = 1 → 找到d = 3
-
用表示式:d ≡ e⁻¹ (mod φ(n)) → d ≡ 7⁻¹ (mod 10)
- d = 3,因为7 × 3 ≡ 1 (mod 10)
所以,d = 3,因为3是7在模10下的逆元。
3. 为什么RSA需要这个关系?
在RSA加密算法中:
- 加密:c = m^e mod n
- 解密:m = c^d mod n
为了保证解密正确,我们需要:
Text
编辑
c^d mod n = (m^e)^d mod n = m^(e*d) mod n根据欧拉定理(如果m和n互质):
Text
编辑
m^φ(n) ≡ 1 mod n所以,如果e*d ≡ 1 mod φ(n),那么:
Text
编辑
m^(e*d) = m^(1 + k*φ(n)) = m * (m^φ(n))^k ≡ m * 1^k = m mod n关键点:d必须是e在模φ(n)下的逆元,才能保证解密正确。
4. 为什么d ≡ e⁻¹ mod φ(n) 是标准表示?
在数学和密码学中,我们通常用:
- a⁻¹ 表示a的逆元
- a⁻¹ mod m 表示a在模m下的逆元
所以,d ≡ e⁻¹ mod φ(n) 是标准的数学表示方式,表示d是e在模φ(n)下的逆元。
5. 通俗总结
| 表达式 | 含义 | 例子(e=7, φ(n)=10) |
|---|---|---|
| e × d ≡ 1 mod φ(n) | d是e的模逆元 | 7 × 3 ≡ 1 mod 10 |
| d ≡ e⁻¹ mod φ(n) | d是e在模φ(n)下的逆元 | 3 ≡ 7⁻¹ mod 10 |
一句话:d ≡ e⁻¹ mod φ(n) 是d是e在模φ(n)下的逆元的数学标准表示,与e × d ≡ 1 mod φ(n)完全等价。
6. 为什么在RSA中需要模逆元?
RSA的核心是:通过公钥(e, n)加密,私钥(d, n)解密。
- 公钥(e, n):用于加密
- 私钥(d, n):用于解密
为了保证加密和解密正确,必须满足e × d ≡ 1 mod φ(n),即d是e在模φ(n)下的逆元。
这就像在普通乘法中,3 × (1/3) = 1,但在模运算中,我们需要找一个整数d,使得e × d ≡ 1 mod φ(n)。
所以,d ≡ e⁻¹ mod φ(n) 是RSA算法中私钥d的数学定义。
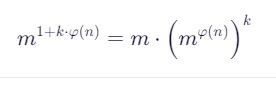
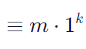 (
(