机器学习——SVM支持向量机详解

一、简介

什么是支持向量机呢？这里我们举一个简单的例子：

想象一下，你是学校的一名体育老师。操场上有一群三年级学生和一群六年级学生混在一起玩耍。现在，上课铃响了，你需要让他们迅速、清晰地分成两个阵营，以便进行不同的活动，你的目标是，在操场上画一条直线，让三年级生站在一边，六年级生站在另一边（蓝色是三年级学生，红色是六年级学生）

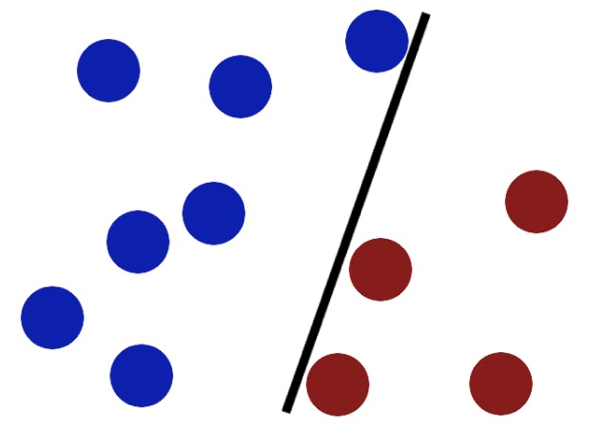
方法一：随便画一条线你可能会大致看一眼，在两组人中间画一条线。这条线确实能把人分开，但它离一些调皮捣蛋、站在队伍边缘的学生非常近问题：

这条线非常"脆弱"。万一有个三年级的学生被推了一下，或者六年级的学生往前跳了一步，他们就越过界线，造成混淆。这条线的容错能力很差

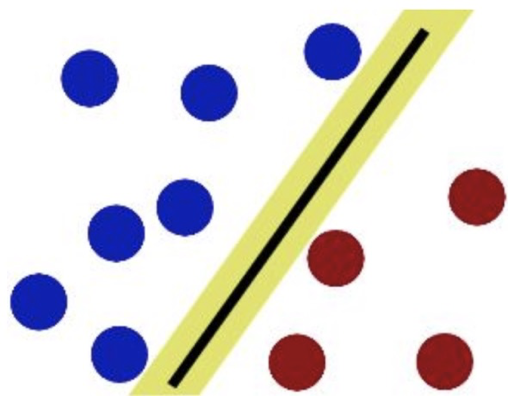
方法二：画一条"最宽"的通道聪明的你首先会观察，找出那群三年级生里最靠近六年级的"先锋"，以及六年级生里最靠近三年级的"先锋"。

然后，你会在不碰到这些学生的前提下，画一条最宽的通道。这条通道的中间线，在SVM中我们称之为

"决策边界"（图中黄色的为过道，黄色中间黑色的线为决策边界）问题：

这样的通道当然很好，因为这条边界离两边最近的学生最远，所以即使有学生稍微动一下，或者有新来的插班生站得比较靠前，他们也不太可能轻易越过这条界线，但是如果学生比较调皮，他们并不听从你的安排，没有整整齐齐的站在两边，那么应该如怎么办呢

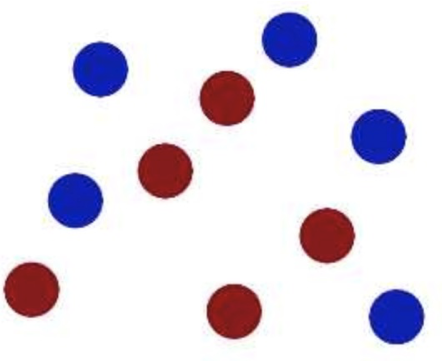
方法三：升维

显然在如下图的站位中，你没有办法通过一条直线将学生分为两类

聪明的你想到了另一种方法，通过一个台阶，让三年级的学生站在台阶上，而让六年级的学生站在台阶下，这样无论他们怎么移动，三年级的学生始终只能在台阶，他们始终是一个类

在以上的例子中，我们称学生为数据，"先锋"学生称为支持向量 ，通道为最优化 ，让学生站在台阶上的思想称为核方法 ，而台阶就是超平面

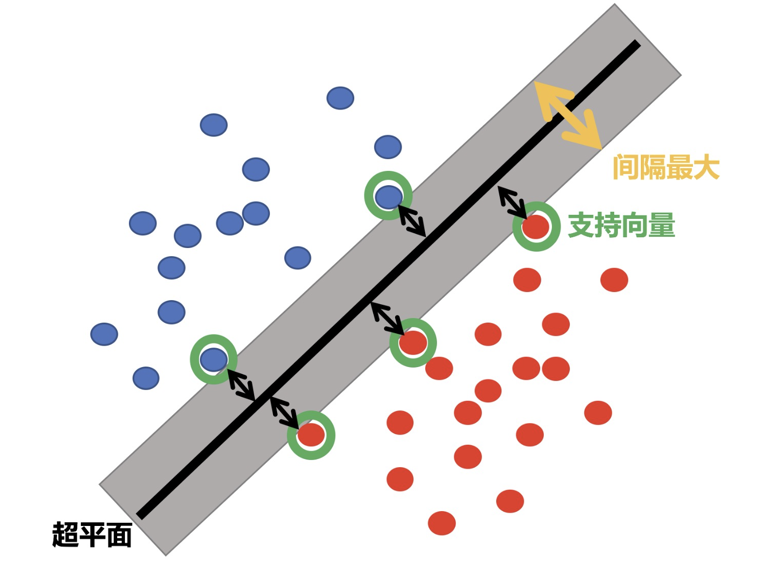
SVM全称是supported vector machine（支持向量机），即寻找到一个超平面使样本分成两类，并且间隔最大
SVM能够执行线性或非线性分类、回归，甚至是异常值检测任务，适用于中小型复杂数据集的分类

1.1 超平面最大间隔

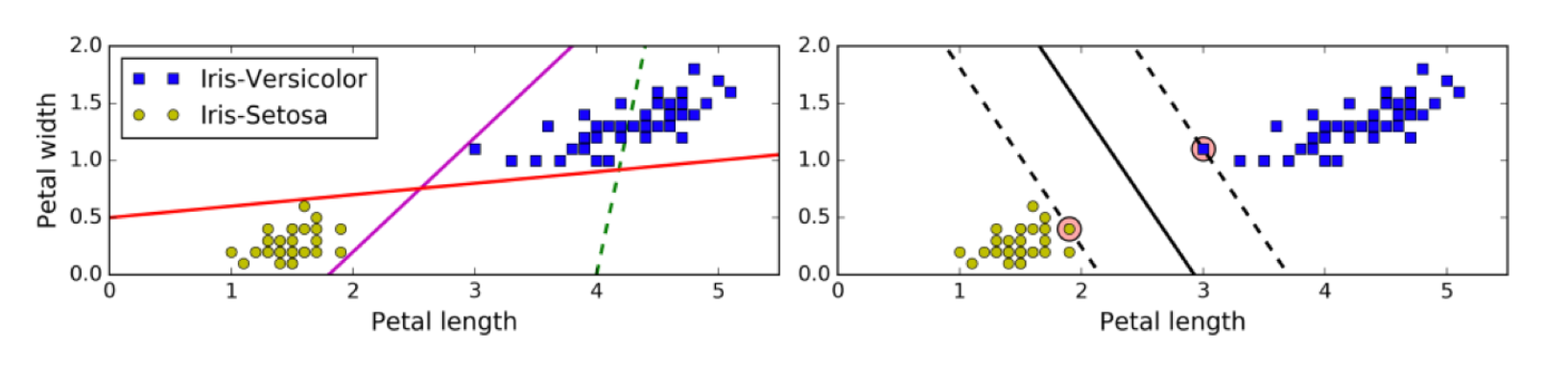
上左图显示了三种可能的线性分类器的决策边界：

虚线所代表的模型表现非常糟糕，甚至都无法正确实现分类。其余两个模型在这个训练集上表现堪称完美，但是它们的决策边界与实例过于接近，导致在面对新实例时，表现可能不会太好

右图中的实线代表SVM分类器的决策边界 ，不仅分离了两个类别，且尽可能远离最近的训练实例

1.2 硬间隔

如果样本线性可分，在所有样本分类都正确的情况下，寻找最大间隔，这就是硬间隔

如果出现异常值、或者样本不能线性可分，此时硬间隔无法实现。

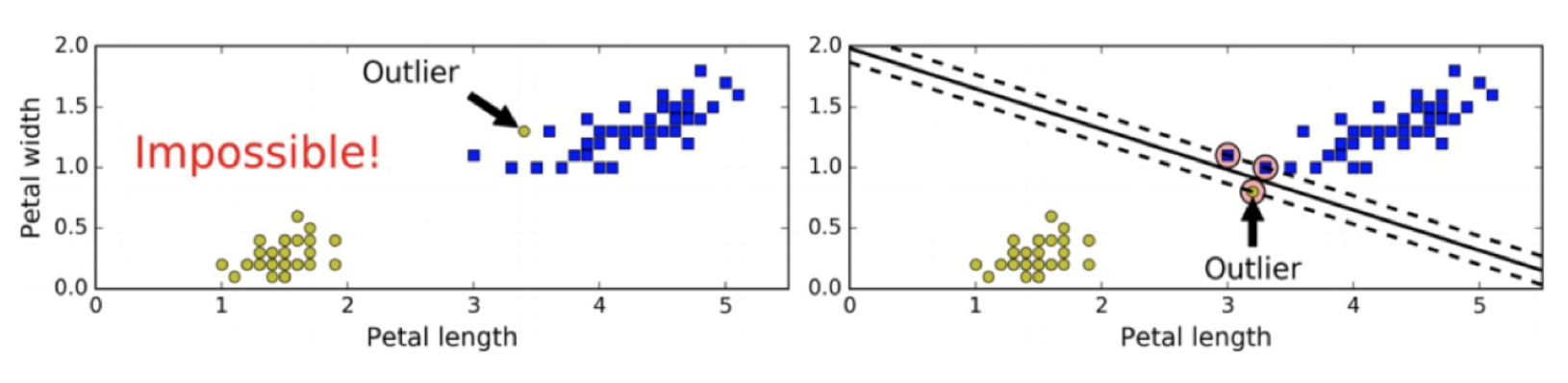
当有一个额外异常值的鸢尾花数据，左图的数据根本找不出硬间隔，而右图最终显示的决策边界与我们之前所看到的无异常值时的决策边界也大不相同，可能无法很好地泛化。

1.3 软间隔和惩罚系数

允许部分样本，在最大间隔之内，甚至在错误的一边，寻找最大间隔，这就是软间隔

目标是尽可能在保持间隔宽阔和限制间隔违例之间找到良好的平衡。

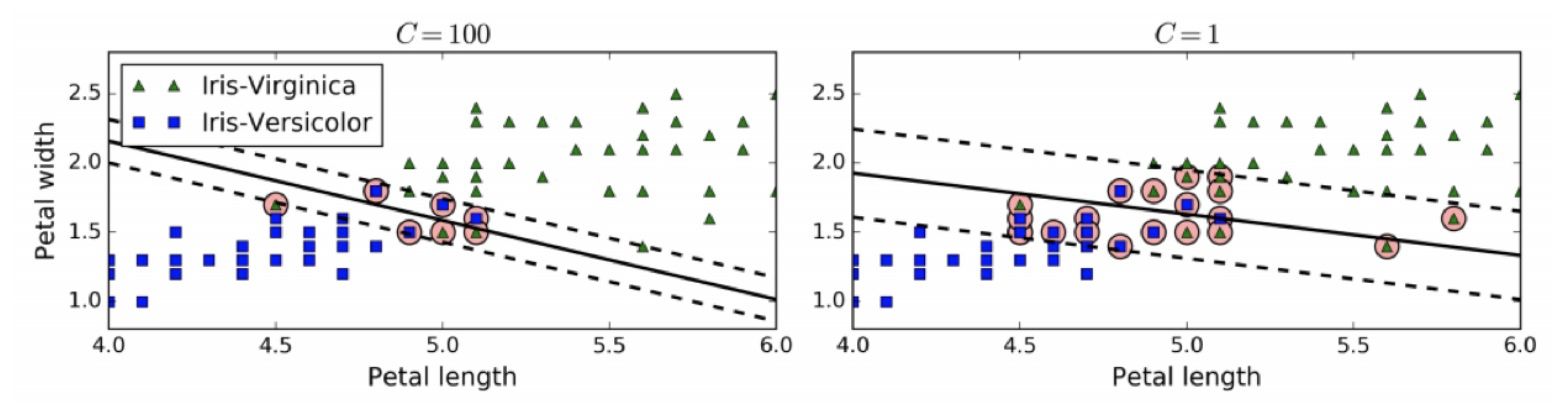
通过惩罚系数C来控制这个平衡：C值越小，则间隔越宽，但是间隔违例也会越多。

左边使用了高C值，分类器的错误样本（间隔违例）较少，但是间隔也较小。

右边使用了低C值，间隔大了很多，但是位于间隔上的实例也更多。

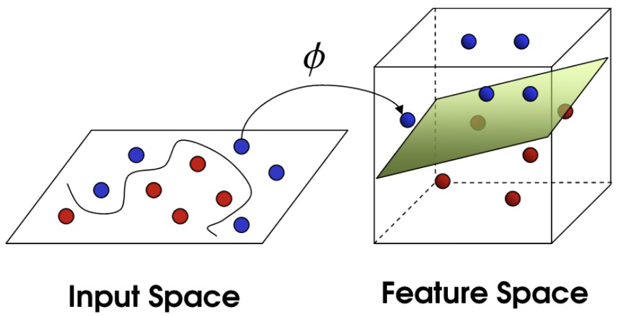
1.4 核函数

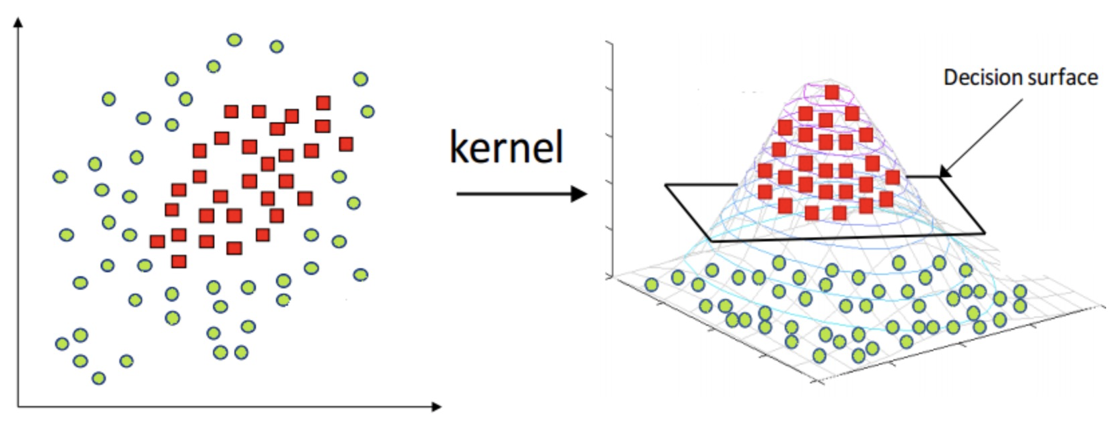
核函数将原始输入空间映射到新的特征空间，使得原本线性不可分的样本在核空间可分

二、SVM算法原理

SVM的思想：要去求一组参数（w，b），使其构建的超平面函数能够最优的分离两个集合

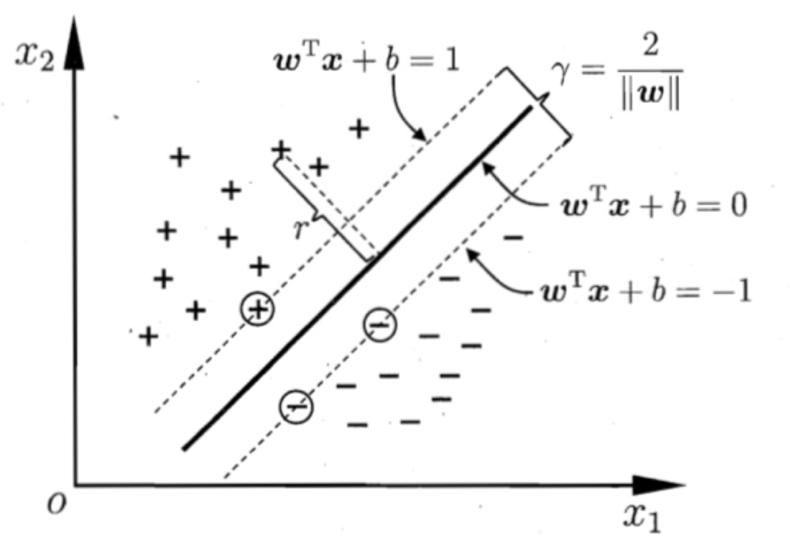
首先我们定义决策边界为：WTx+b=0W^Tx+b=0WTx+b=0，两边的支持向量所在的边界为wTx+b=1w^Tx+b=1wTx+b=1和wTx+b=−1w^Tx+b=-1wTx+b=−1，这里的±1\pm1±1只是为了好计算，等于多少都可以
我们知道，点到直线的距离可以写成：d=∣Ax0+By0+C∣A2+B2d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}d=A2+B2 ∣Ax0+By0+C∣
因此点到超平面的距离为：r=∣wTx+b∣∣∣w∣∣r=\frac{|\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b|}{||\boldsymbol{w}||}r=∣∣w∣∣∣wTx+b∣
由于支持向量在wTx+b=1w^Tx+b=1wTx+b=1线段上，因此支持向量距离超平面的距离为：r=1∣∣w∣∣r=\frac{1}{||\boldsymbol{w}||}r=∣∣w∣∣1
因此最大间距为：r=2∣∣w∣∣r=\frac{2}{||\boldsymbol{w}||}r=∣∣w∣∣2
我们知道数据集中的点需要满足的条件为：{wTxi+b⩾+1,yi=+1;wTxi+b⩽−1,yi=−1.\left.\left\{ \begin{array} {ll}\boldsymbol{w}^\mathrm{T}\boldsymbol{x}i+b\geqslant+1, & y_i=+1; \\ \boldsymbol{w}^\mathrm{T}\boldsymbol{x}i+b\leqslant-1, & y_i=-1. \end{array}\right.\right.{wTxi+b⩾+1,wTxi+b⩽−1,yi=+1;yi=−1.
我们希望在将所以样本正确分类的情况下，试下间隔最大化，因此目标函数可以写为：max⁡w,b=2∥w∥s.t. yi(wTxi+b)≥1,i=1,2,⋯ ,m\begin{aligned} & \max{w,b}=\frac{2}{\|w\|} \\ & \mathrm{s.t.~}y_i\left(w^Tx_i+b\right)\geq1,i=1,2,\cdots,m \end{aligned}w,bmax=∥w∥2s.t. yi(wTxi+b)≥1,i=1,2,⋯,m
最大值比较难求，我们可以将其转换为最小化问题：min⁡w,b=12∥w∥2s.t. yi(wTxi+b)≥1,i=1,2,⋯ ,m\begin{aligned} & \min{w,b}=\frac{1}{2}\|w\|^2 \\ & \mathrm{s.t.~}y_i\left(w^Tx_i+b\right)\geq1,i=1,2,\cdots,m \end{aligned}w,bmin=21∥w∥2s.t. yi(wTxi+b)≥1,i=1,2,⋯,m

其中∥w∥\|w\|∥w∥范数为：sqrt(w12+w22+...+wn2)sqrt(w_1^2+w_2^2+...+w_n^2)sqrt(w12+w22+...+wn2)，加上平凡之后将根号去掉，不影响优化目标
1/21/21/2是为了求导的时候，能够将系数去掉

在某种条件下，求最值，很容易联想到拉格朗日乘数法，因此我们构造：L(w,b,α)=12∥w∥2−∑i=1nαi(yi(wT⋅Φ(xi)+b)−1)，其中Φ(xi)为核函数L(w,b,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^n\alpha_i\left(y_i\left(w^T\cdot\Phi\left(x_i\right)+b\right)-1\right)，其中\Phi(x_i)为核函数L(w,b,α)=21∥w∥2−i=1∑nαi(yi(wT⋅Φ(xi)+b)−1)，其中Φ(xi)为核函数
在这个式子中，我们希望后面的一坨尽可能的大，而整个式子尽可能的小，因此我们可以将其转换一下：min⁡w,bmax⁡αL(w,b,α)<=>max⁡αmin⁡w,bL(w,b,α)\min_{w,b}\max_{\alpha}L(w,b,\alpha)<=>\max_{\alpha}\min_{w,b}L(w,b,\alpha)w,bminαmaxL(w,b,α)<=>αmaxw,bminL(w,b,α)
对偶问题转换：
接下来我们对w求偏导，并令其等于0：∂L∂w=12∣∣w∣∣2−∑i=1nαi(yiwTφ(xi)+yib−1)=0=12∣∣w∣∣2−∑i=1nαiyiwTφ(xi)+αiyib−αi=0=w−∑i=1nαiyiφ(xi)=0\begin{aligned} \frac{\partial L}{\partial w} & =\frac{1}{2}||w||^2-\sum_{i=1}^n\alpha_i\left(y_iw^T\varphi\left(x_i\right)+y_ib-1\right)=0 \\ & =\frac{1}{2}||w||^2-\sum_{i=1}^n\alpha_iy_iw^T\varphi\left(x_i\right)+\alpha_iy_ib-\alpha_i=0 \\ & =w-\sum_{i=1}^n\alpha_iy_i\varphi\left(x_i\right)=0 \end{aligned}∂w∂L=21∣∣w∣∣2−i=1∑nαi(yiwTφ(xi)+yib−1)=0=21∣∣w∣∣2−i=1∑nαiyiwTφ(xi)+αiyib−αi=0=w−i=1∑nαiyiφ(xi)=0
得出：w=∑i=1nαiyiφ(xi)w=\sum_{i=1}^n\alpha_iy_i\varphi\left(x_i\right)w=i=1∑nαiyiφ(xi)
同理，我们对b求偏导得：∂L∂w=12∥w∥2−∑i=1nαiyiwTφ(xi)+αiyib−αi=∑i=1nαiyi=0\begin{aligned} \frac{\partial L}{\partial w} & =\frac{1}{2}\|w\|^2-\sum_{i=1}^n\alpha_iy_iw^T\varphi\left(x_i\right)+\alpha_iy_ib-\alpha_i \\ & =\sum_{i=1}^n\alpha_iy_i=0 \end{aligned}∂w∂L=21∥w∥2−i=1∑nαiyiwTφ(xi)+αiyib−αi=i=1∑nαiyi=0
带入原拉格拉日公式：L(w,b,α)=12∣∣w∣∣2−∑i=1nαi(yi(wTφ(xi)+b)−1)=12wTw−∑i=1n(αiyiwTφ(xi)+αiyib−αi)=12wTw−∑i=1nαiyiwTφ(xi)−b∑i=1naiyi+∑i=1nαi=12wTw−∑i=1nαiyiwTφ(xi)+∑i=1nαi=12wT∑i=1nαiyiφ(xi)−wT∑i=1nαiyiφ(xi)+∑i=1nαi=∑i=1nαi−12(∑i=1nαiyiφ(xi))T⋅∑i=1nαiyiφ(xi)=∑i=1nαi−∑i=1n∑j=1nαiαjyiyjφT(xi)φ(xj)\begin{aligned} & L(w,b,\alpha)=\frac{1}{2}||w||^{2}-\sum_{i=1}^{n}\alpha_{i}(y_{i}(w^{T}\varphi(x_{i})+b)-1) \\ & =\frac{1}{2}w^{T}w-\sum_{i=1}^{n}(\alpha_{i}y_{i}w^{T}\varphi(x_{i})+\alpha_{i}y_{i}b-\alpha_{i}) \\ & =\frac{1}{2}w^{T}w-\sum_{i=1}^{n}\alpha_{i}y_{i}w^{T}\varphi(x_{i})-b\sum_{i=1}^{n}a_{i}y_{i}+\sum_{i=1}^{n}\alpha_{i} \\ & =\frac{1}{2}w^{T}w-\sum_{i=1}^{n}\alpha_{i}y_{i}w^{T}\varphi(x_{i})+\sum_{i=1}^{n}\alpha_{i} \\ & =\frac{1}{2}w^{T}\sum_{i=1}^{n}\alpha_{i}y_{i}\varphi(x_{i})-w^{T}\sum_{i=1}^{n}\alpha_{i}y_{i}\varphi(x_{i})+\sum_{i=1}^{n}\alpha_{i} \\ & =\sum_{i=1}^{n}\alpha_{i}-\frac{1}{2}\left(\sum_{i=1}^{n}\alpha_{i}y_{i}\varphi(x_{i})\right)^{T}\cdot\sum_{i=1}^{n}\alpha_{i}y_{i}\varphi(x_{i}) \\ & =\sum_{i=1}^{n}\alpha_{i}-\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y_{i}y_{j}\varphi^{T}(x_{i})\varphi(x_{j}) \end{aligned}L(w,b,α)=21∣∣w∣∣2−i=1∑nαi(yi(wTφ(xi)+b)−1)=21wTw−i=1∑n(αiyiwTφ(xi)+αiyib−αi)=21wTw−i=1∑nαiyiwTφ(xi)−bi=1∑naiyi+i=1∑nαi=21wTw−i=1∑nαiyiwTφ(xi)+i=1∑nαi=21wTi=1∑nαiyiφ(xi)−wTi=1∑nαiyiφ(xi)+i=1∑nαi=i=1∑nαi−21(i=1∑nαiyiφ(xi))T⋅i=1∑nαiyiφ(xi)=i=1∑nαi−i=1∑nj=1∑nαiαjyiyjφT(xi)φ(xj)
此时，先求解当 α 是什么值时，该值会变得很大，之后再求解 w, b 值，最后就变成了极大极小值问题

求解当 α 什么值的时候该公式值最大：a∗=arg⁡max⁡α(∑i=1nαi−12∑i,j=1nαiαjyiyjΦT(xi)Φ(xj))a^*=\arg\max_\alpha\left(\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\Phi^T\left(x_i\right)\Phi\left(x_j\right)\right)a∗=argαmax(i=1∑nαi−21i,j=1∑nαiαjyiyjΦT(xi)Φ(xj))
将上面的问题转换为极小值问题：min⁡α12∑i=1n∑j=1nαiαjyiyj(Φ(xi)⋅Φ(xj))−∑i=1nαis.t. ∑i=1nαiyi=0αi≥0,i=1,2,...,n\min_\alpha\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_j\left(\Phi\left(x_i\right)\cdot\Phi\left(x_j\right)\right)-\sum_{i=1}^n\alpha_i \\ \mathrm{s.t.~}\sum_{i=1}^n\alpha_iy_i=0 \\ \alpha_i\geq0,\quad i=1,2,\ldots,nαmin21i=1∑nj=1∑nαiαjyiyj(Φ(xi)⋅Φ(xj))−i=1∑nαis.t. i=1∑nαiyi=0αi≥0,i=1,2,...,n
将训练样本带入上述公式，求解出 α 值，然后将 α 带入下面公式计算出w，b：w∗=∑i=1Nαi∗yiΦ(xi)b∗=yi−∑i=1Nαi∗yi(Φ(xi)⋅Φ(xj))\begin{aligned} & w^{*}=\sum_{i=1}^N\alpha_i^*y_i\Phi\left(x_i\right) \\ & b^{*}=y_i-\sum_{i=1}^N\alpha_i^*y_i\left(\Phi\left(x_i\right)\cdot\Phi\left(x_j\right)\right) \end{aligned}w∗=i=1∑Nαi∗yiΦ(xi)b∗=yi−i=1∑Nαi∗yi(Φ(xi)⋅Φ(xj))
最后求导分离超平面：w∗Φ(x)+b∗=0w^*\Phi(x)+b^*=0w∗Φ(x)+b∗=0

三、核函数

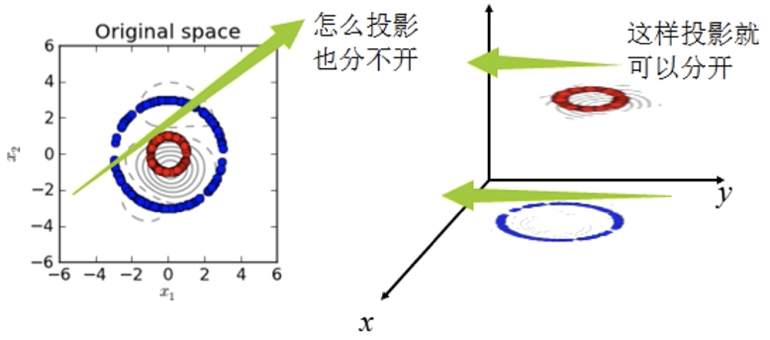
核函数，是将原始输入空间映射到新的特征空间，从而，使得原本线性不可分的样本可能在核空间可分
核函数分类：

高斯核函数使用较多。
1. 线性核：一般是不增加数据维度，而是预先计算内积，提高速度
2. 多项式核：一般是通过增加多项式特征，提升数据维度，并计算内积
3. 高斯核（RBF、径向基函数）：一般是通过将样本投射到无限维空间，使得原来不可分的数据变得可分。
高斯核函数：

在高斯核中，为了便于计算，我们将K(xi,xj)=exp⁡(−∥xi−xj∥22σ2)K(\boldsymbol{x}_i,\boldsymbol{x}_j)=\exp\left(-\frac{\|\boldsymbol{x}_i-\boldsymbol{x}_j\|^2}{2\sigma^2}\right)K(xi,xj)=exp(−2σ2∥xi−xj∥2)转换为K(x, y)=e−γ∣∣x−y∣∣2\mathrm{K(x,~y)}=e^{-\gamma||x-y||^{2}}K(x, y)=e−γ∣∣x−y∣∣2
其中gamma是超参数，作用与标准差相反，gamma越大，高斯分布越窄,gamma越小，高斯分布越宽

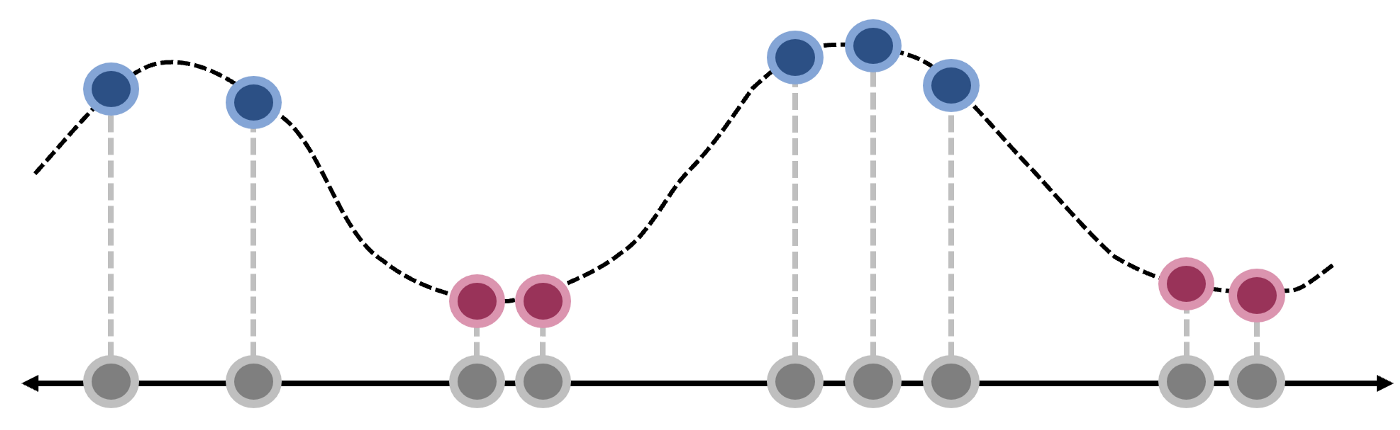
我们希望找到一种方法，用一条线将数据完美分类。如果只从1维的角度考虑，这是一项不可能完成的任务，但可以用升维度的办法来解决问题

让我们引入一个函数 f(x)，图像如下图所示。将 x 的每个值映射到其对应的输出。使得所有蓝点在Y轴的输出更大，而红点在Y轴的输出偏小。此时，我们可以使用一条水平线将数据完美分类

四、案例

python 复制代码

import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.pipeline import Pipeline
from plot_util import plot_decision_boundary
# 初始化数据集
x,y = datasets.make_moons(n_samples=200, noise=0.15 , random_state=22)
plt.scatter(x[y==0 , 0] , x[y==0 , 1] , c="red")
plt.scatter(x[y==1 , 0] , x[y==1 , 1] , c="blue")
plt.show()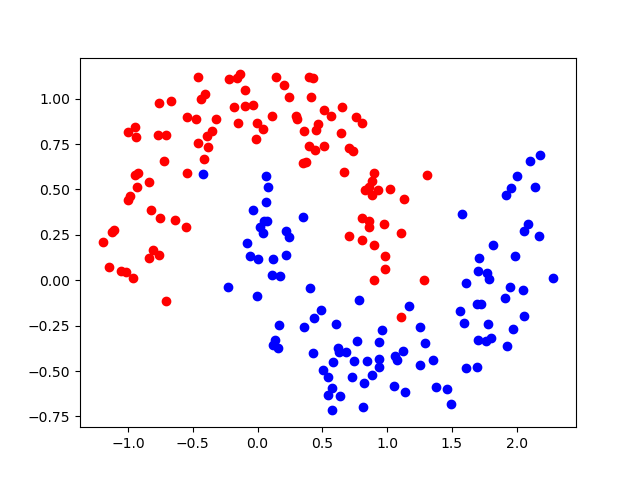

python 复制代码

# 定义一个高斯核函数，其中Pipeline为管道执行，依次执行了标准化和核函数定义
def RBFKernelSVC(gamma=1.0):
    return Pipeline([
        ('scaler', StandardScaler()),
        ('svc', SVC(kernel='rbf', gamma=gamma))
    ])
# 使用gamma=1测试
model1 = RBFKernelSVC(gamma=1.0)
model1.fit(x,y)
plot_decision_boundary(model1,axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0 , 0] , x[y==0 , 1] , c="red")
plt.scatter(x[y==1 , 0] , x[y==1 , 1] , c="blue")
plt.show()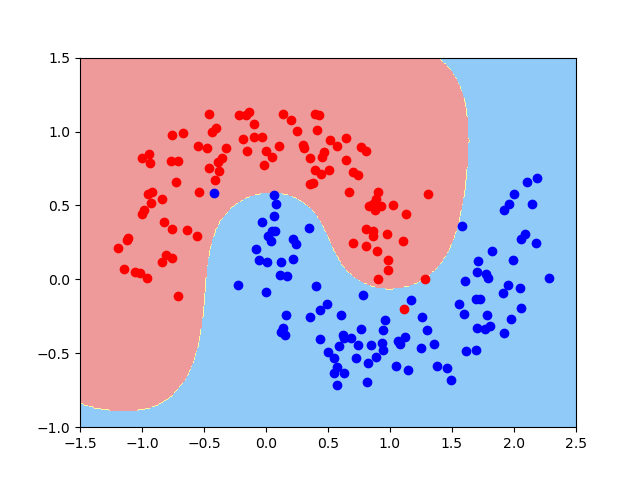

python 复制代码

# 将gamma变大，可以看到存在有过拟合的现象
model2 = RBFKernelSVC(gamma=100)
model2.fit(x,y)
plot_decision_boundary(model2,axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0 , 0] , x[y==0 , 1] , c="red")
plt.scatter(x[y==1 , 0] , x[y==1 , 1] , c="blue")
plt.show()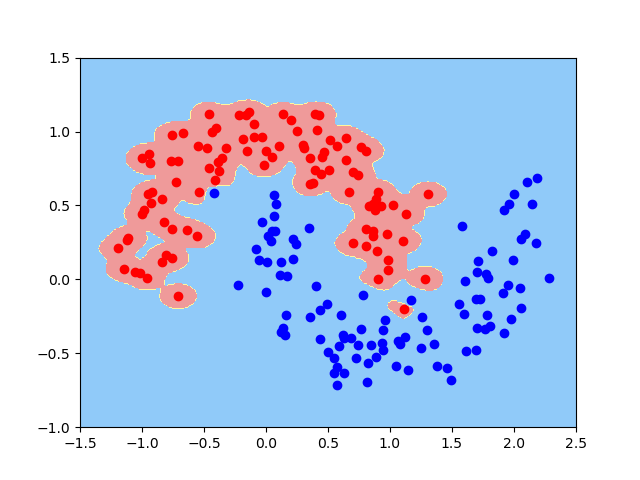

python 复制代码

# 将gamma缩小，可以看到有欠拟合的现象
model3 = RBFKernelSVC(gamma=0.1)
model3.fit(x,y)
plot_decision_boundary(model3,axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(x[y==0 , 0] , x[y==0 , 1] , c="red")
plt.scatter(x[y==1 , 0] , x[y==1 , 1] , c="blue")
plt.show()

其中plot_util的函数为：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def plot_decision_boundary(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_map = ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])

    # plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)
    plt.contourf(x0,x1,zz,cmap=custom_map)

def plot_decision_boundary_svc(model,axis):
    x0,x1 = np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)).reshape(-1,1),
        np.linspace(axis[2],axis[3],int((axis[3]-axis[2])*100)).reshape(-1,1)
    )
    X_new = np.c_[x0.ravel(),x1.ravel()]
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_map = ListedColormap(["#EF9A9A","#FFF59D","#90CAF9"])

    # plt.contourf(x0,x1,zz,linewidth=5,cmap=custom_map)
    plt.contourf(x0,x1,zz,cmap=custom_map)


    w= model.coef_[0]
    b = model.intercept_[0]
    # w0* x0 + w1* x1+ b = 0
    #=>x1 = -w0/w1 * x0 - b/w1
    plot_x = np.linspace(axis[0],axis[1],200)
    up_y = -w[0]/w[1]* plot_x - b/w[1]+ 1/w[1]
    down_y = -w[0]/w[1]* plot_x - b/w[1]-1/w[1]
    up_index =(up_y >= axis[2])&(up_y <= axis[3])
    down_index =(down_y>= axis[2])&(down_y<= axis[3])
    plt.plot(plot_x[up_index],up_y[up_index],color="black")
    plt.plot(plot_x[down_index],down_y[down_index],color="black")

因此我们可以得出结论：

gamma越大，模型过拟合风险越高
gamma越小，模型欠拟合风险越高