第7章 n步时序差分 n步时序差分预测

第7章 n步时序差分

n步时序差分（n-step TD）方法是蒙特卡洛（MC）方法与时序差分（TD）方法的统一推广。蒙特卡洛方法使用完整回报，对应 n→∞n \to \inftyn→∞ 的极端情况；单步TD方法（如TD(0)）对应 n=1n = 1n=1 的极端情况。中间的 nnn 值通常能取得比两种极端方法更好的性能。

在单步TD中，动作更新频率与自举（bootstrapping）的时间跨度被绑定为同一个时间步长，导致灵活性不足。实际应用中，希望动作能快速响应变化（高频更新），但自举需要在状态有显著变化的时间段内进行才有效。 n步方法通过延长自举的时间窗口（使用n步回报），解耦了更新频率与自举跨度，提升了灵活性和效果。

$!NOTE$
TD(0) 复习

TD(0)（单步时序差分）是一种基于自举（bootstrapping）的无模型强化学习方法，用于在线估计给定策略 π\piπ 的状态价值函数 vπ(s)v_\pi(s)vπ(s)。它在每一步根据即时奖励和下一个状态的当前价值估计来更新当前状态的价值。

在每个时间步 ttt，智能体从状态 StS_tSt 执行动作，获得奖励 Rt+1R_{t+1}Rt+1 并转移到状态 St+1S_{t+1}St+1。TD(0) 的价值更新公式为：
V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)] V(S_t) \leftarrow V(S_t) + \alpha \left[ R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right] V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]

其中：

α∈(0,1]\alpha \in (0,1]α∈(0,1] 是学习率，

γ∈[0,1]\gamma \in [0,1]γ∈[0,1] 是折扣因子，

Rt+1+γV(St+1)R_{t+1} + \gamma V(S_{t+1})Rt+1+γV(St+1) 是TD目标，

δt=Rt+1+γV(St+1)−V(St)\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)δt=Rt+1+γV(St+1)−V(St) 称为TD误差。

特点：

在线更新：每走一步即可更新，无需等到回合结束。

自举：使用当前价值函数估计 V(St+1)V(S_{t+1})V(St+1) 来更新 V(St)V(S_t)V(St)，而非依赖完整回报。

偏差-方差权衡：相比蒙特卡洛方法（无偏但高方差），TD(0) 引入一定偏差，但通常具有更低的方差，学习更稳定。

TD(0) 主要用于策略评估 （预测问题），即在固定策略 π\piπ 下估计 vπv_\pivπ。它可作为控制算法（如SARSA或Q-learning）的基础组件。

与蒙特卡洛方法的对比 ，蒙特卡洛方法使用完整回报 Gt=∑k=0T−t−1γkRt+k+1G_t = \sum_{k=0}^{T-t-1} \gamma^k R_{t+k+1}Gt=∑k=0T−t−1γkRt+k+1 作为目标，需等待回合结束；TD(0) 使用一步回报 Rt+1+γV(St+1)R_{t+1} + \gamma V(S_{t+1})Rt+1+γV(St+1)，可立即更新。

nnn 步时序差分预测

算法实现

MC 使用从状态 StS_tSt 到终止状态的完整回报更新价值； TD(0) 仅用一步奖励和下一状态的价值估计进行自举；n步TD 使用前 nnn 步的实际奖励，再用第 nnn 步之后的状态价值估计进行自举。n步时序差分构成一个从 n=1n=1n=1到 n→∞n \to \inftyn→∞的连续谱系。

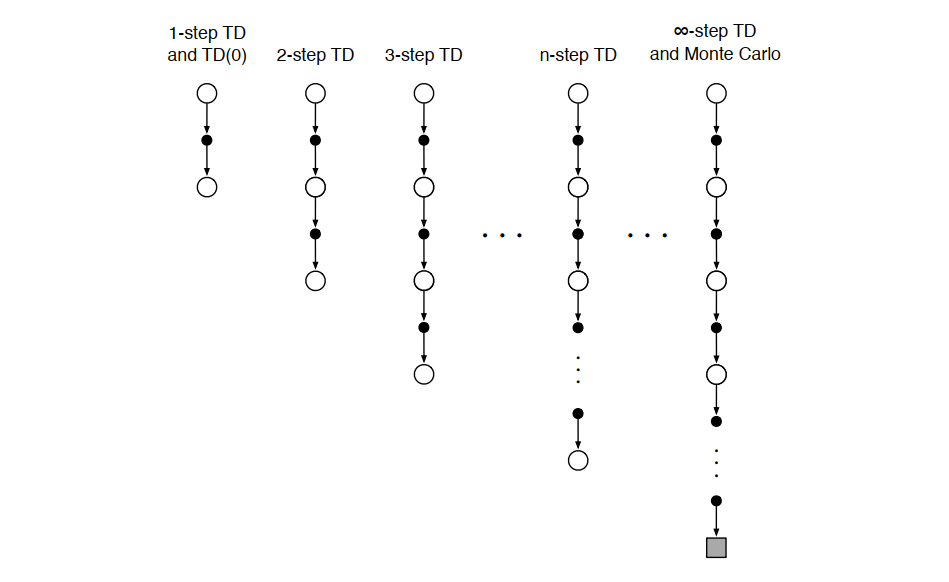
在固定策略 π\piπ 下，对状态 StS_tSt 的价值估计 vπ(St)v_\pi(S_t)vπ(St) 可通过不同长度的回报目标进行更新。

**TD(0)**的回报目标是 Gt:t+1≐Rt+1+γVt(St+1)G_{t:t+1} \doteq R_{t+1} + \gamma V_t(S_{t+1})Gt:t+1≐Rt+1+γVt(St+1)；使用1步实际奖励，后续用 Vt(St+1)V_t(S_{t+1})Vt(St+1) 自举替代了完整回报中从 Rt+2R_{t+2}Rt+2 开始的部分。
2步TD 的回报目标是 Gt:t+2≐Rt+1+γRt+2+γ2Vt+1(St+2)G_{t:t+2} \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 V_{t+1}(S_{t+2})Gt:t+2≐Rt+1+γRt+2+γ2Vt+1(St+2)，使用前2步的实际奖励，第3步及之后用 γ2Vt+1(St+2)\gamma^2 V_{t+1}(S_{t+2})γ2Vt+1(St+2) 自举；替代了 Rt+3,Rt+4,...R_{t+3}, R_{t+4}, \dotsRt+3,Rt+4,...。
n步TD 是 KaTeX parse error: \tag works only in display equations，使用前 nnn 步实际奖励，第 n+1n+1n+1 步起用价值估计自举；适用于 n≥1n \geq 1n≥1 且 0≤t<T−n0 \leq t < T - n0≤t<T−n。
MC 则是 Gt=Rt+1+γRt+2+γ2Rt+3+⋯+γT−t−1RTG_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots + \gamma^{T-t-1} R_TGt=Rt+1+γRt+2+γ2Rt+3+⋯+γT−t−1RT，使用从 ttt 到终止时刻 TTT 的完整实际回报；相当于 n→∞n \to \inftyn→∞ 的极限情况。

给定状态-奖励序列 St,Rt+1,St+1,Rt+2,...,RT,STS_t, R_{t+1}, S_{t+1}, R_{t+2}, \ldots, R_T, S_TSt,Rt+1,St+1,Rt+2,...,RT,ST，n步回报 定义为：
Gt:t+n≐Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n),(7.1) G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}), \tag{7.1} Gt:t+n≐Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n),(7.1)

其中：

n≥1n \geq 1n≥1，
0≤t<T0 \leq t < T0≤t<T，
若 t+n≥Tt + n \geq Tt+n≥T（即超出终止时刻），则定义 V(St+n)≐0V(S_{t+n}) \doteq 0V(St+n)≐0，此时 Gt:t+n=GtG_{t:t+n} = G_tGt:t+n=Gt（完整回报）。

在时刻 t+nt+nt+n，使用 Gt:t+nG_{t:t+n}Gt:t+n 对状态 StS_tSt 的价值进行更新：
V(St)←V(St)+α[Gt:t+n−V(St)],0≤t<T,(7.2) V(S_t) \leftarrow V(S_t) + \alpha \big[ G_{t:t+n} - V(S_t) \big], \quad 0 \leq t < T, \tag{7.2} V(St)←V(St)+α[Gt:t+n−V(St)],0≤t<T,(7.2)

其他状态的价值保持不变。

算法特点 是更新存在 nnn 步延迟，必须等到 t+nt+nt+n 时刻才能计算 Gt:t+nG_{t:t+n}Gt:t+n；前 n−1n-1n−1 步无更新，需在幕终止后补足剩余更新；同时使用环形缓冲区（索引对 n+1n+1n+1 取模）高效存储最近的 n+1n+1n+1 个状态和奖励。

n步TD算法（预测问题，估计 V≈vπV \approx v_\piV≈vπ）：

输入：策略 π\piπ
参数：步长 α∈(0,1]\alpha \in (0,1]α∈(0,1]，正整数 nnn
初始化 ：对所有 s∈Ss \in \mathcal{S}s∈S，任意初始化 V(s)V(s)V(s)

对每幕执行：

初始化并存储 S0S_0S0（非终止状态）
设 T←∞T \leftarrow \inftyT←∞
对 t=0,1,2,...t = 0, 1, 2, \ldotst=0,1,2,... 执行：
- 若 t<Tt < Tt<T：
  - 根据 π(⋅∣St)\pi(\cdot \mid S_t)π(⋅∣St) 选择动作
  - 观察并存储 Rt+1R_{t+1}Rt+1 和 St+1S_{t+1}St+1
  - 若 St+1S_{t+1}St+1 为终止状态，则 T←t+1T \leftarrow t + 1T←t+1
- 计算 τ←t−n+1\tau \leftarrow t - n + 1τ←t−n+1
- 若 τ≥0\tau \geq 0τ≥0：
  - 计算部分回报：
    G←∑i=τ+1min⁡(τ+n, T)γi−τ−1Ri G \leftarrow \sum_{i=\tau+1}^{\min(\tau+n,\,T)} \gamma^{i-\tau-1} R_i G←i=τ+1∑min(τ+n,T)γi−τ−1Ri
  - 若 τ+n<T\tau + n < Tτ+n<T，则追加自举项：
    G←G+γnV(Sτ+n) G \leftarrow G + \gamma^n V(S_{\tau+n}) G←G+γnV(Sτ+n)
  - 更新价值函数：
    V(Sτ)←V(Sτ)+α[G−V(Sτ)] V(S_\tau) \leftarrow V(S_\tau) + \alpha \big[ G - V(S_\tau) \big] V(Sτ)←V(Sτ)+α[G−V(Sτ)]
- 若 τ≥T−1\tau \geq T - 1τ≥T−1，则结束本幕

$!NOTE$
代码例子

n = 2（两步TD）

折扣因子 γ=1\gamma = 1γ=1（简化计算）

步长 α=0.5\alpha = 0.5α=0.5

状态空间：S={A,B,C,D,E}S = \{A, B, C, D, E\}S={A,B,C,D,E}，其中 EEE 是终止状态

初始价值函数：对所有状态 sss，设 V(s)=0V(s) = 0V(s)=0

策略 π\piπ 固定，产生如下一幕轨迹（状态-奖励序列）：

S0=A, R1=1, S1=B, R2=2, S2=C, R3=3, S3=D, R4=4, S4=E (终止)S_0 = A,\ R_1 = 1,\ S_1 = B,\ R_2 = 2,\ S_2 = C,\ R_3 = 3,\ S_3 = D,\ R_4 = 4,\ S_4 = E\ (\text{终止})S0=A, R1=1, S1=B, R2=2, S2=C, R3=3, S3=D, R4=4, S4=E (终止)

因此，终止时刻 T=4T = 4T=4（因为 S4=ES_4 = ES4=E 是终止状态）。

我们按时间步 t=0,1,2,...t = 0, 1, 2, \dotst=0,1,2,... 模拟算法流程。

t = 0

t<Tt < Tt<T（0 < 4）→ 执行动作（已给出轨迹）

存储 R1=1R_1 = 1R1=1, S1=BS_1 = BS1=B

S1≠ES_1 \neq ES1=E → TTT 仍为 ∞\infty∞

τ=0−1=−1<0\tau = 0 - 1 = -1 < 0τ=0−1=−1<0 → 不更新

t = 1

t<Tt < Tt<T → 继续

存储 R2=2R_2 = 2R2=2, S2=CS_2 = CS2=C

非终止 → T=∞T = \inftyT=∞

τ=1−1=0≥0\tau = 1 - 1 = 0 \geq 0τ=1−1=0≥0 → 可以更新状态 S0=AS_0 = AS0=A

计算回报 GGG：

min⁡(τ+n,T)=min⁡(0+2,4)=2\min(\tau + n, T) = \min(0 + 2, 4) = 2min(τ+n,T)=min(0+2,4)=2

G=∑i=12γi−0−1Ri=γ0R1+γ1R2=1⋅1+1⋅2=3 G = \sum_{i=1}^{2} \gamma^{i - 0 - 1} R_i = \gamma^0 R_1 + \gamma^1 R_2 = 1 \cdot 1 + 1 \cdot 2 = 3 G=i=1∑2γi−0−1Ri=γ0R1+γ1R2=1⋅1+1⋅2=3

检查是否 τ+n<T\tau + n < Tτ+n<T：0+2=2<40 + 2 = 2 < 40+2=2<4 → 是，需加自举项

G←G+γ2V(S2)=3+12⋅V(C)=3+0=3G \leftarrow G + \gamma^2 V(S_{2}) = 3 + 1^2 \cdot V(C) = 3 + 0 = 3G←G+γ2V(S2)=3+12⋅V(C)=3+0=3

更新 V(S0)=V(A)V(S_0) = V(A)V(S0)=V(A)：
V(A)←V(A)+α[G−V(A)]=0+0.5(3−0)=1.5 V(A) \leftarrow V(A) + \alpha [G - V(A)] = 0 + 0.5 (3 - 0) = 1.5 V(A)←V(A)+α[G−V(A)]=0+0.5(3−0)=1.5

当前价值：
V(A)=1.5V(A)=1.5V(A)=1.5, 其余仍为 0。

t = 2

t<Tt < Tt<T → 继续

存储 R3=3R_3 = 3R3=3, S3=DS_3 = DS3=D

非终止 → T=∞T = \inftyT=∞

τ=2−1=1≥0\tau = 2 - 1 = 1 \geq 0τ=2−1=1≥0 → 更新 S1=BS_1 = BS1=B

计算 GGG：

min⁡(1+2,4)=3\min(1+2, 4) = 3min(1+2,4)=3

G=R2+γR3=2+1⋅3=5 G = R_2 + \gamma R_3 = 2 + 1 \cdot 3 = 5 G=R2+γR3=2+1⋅3=5

τ+n=3<4\tau + n = 3 < 4τ+n=3<4 → 加自举项：G←5+γ2V(S3)=5+V(D)=5+0=5G \leftarrow 5 + \gamma^2 V(S_3) = 5 + V(D) = 5 + 0 = 5G←5+γ2V(S3)=5+V(D)=5+0=5

更新 V(B)V(B)V(B)：
V(B)←0+0.5(5−0)=2.5 V(B) \leftarrow 0 + 0.5 (5 - 0) = 2.5 V(B)←0+0.5(5−0)=2.5

当前价值：
V(A)=1.5V(A)=1.5V(A)=1.5, V(B)=2.5V(B)=2.5V(B)=2.5, 其余为 0。

t = 3

t<Tt < Tt<T → 继续

存储 R4=4R_4 = 4R4=4, S4=ES_4 = ES4=E

S4S_4S4 是终止状态 → 设 T=4T = 4T=4

τ=3−1=2≥0\tau = 3 - 1 = 2 \geq 0τ=3−1=2≥0 → 更新 S2=CS_2 = CS2=C

计算 GGG：

min⁡(2+2,4)=min⁡(4,4)=4\min(2+2, 4) = \min(4,4) = 4min(2+2,4)=min(4,4)=4

G=R3+γR4=3+1⋅4=7 G = R_3 + \gamma R_4 = 3 + 1 \cdot 4 = 7 G=R3+γR4=3+1⋅4=7

检查：τ+n=2+2=4\tau + n = 2 + 2 = 4τ+n=2+2=4，而 T=4T = 4T=4，所以 τ+n=T\tau + n = Tτ+n=T → 不小于 T → 不加自举项

（因为从 S4=ES_4 = ES4=E 开始无后续状态，V(E)=0V(E) = 0V(E)=0，且算法规定此时 G=GtG = G_tG=Gt）

更新 V(C)V(C)V(C)：
V(C)←0+0.5(7−0)=3.5 V(C) \leftarrow 0 + 0.5 (7 - 0) = 3.5 V(C)←0+0.5(7−0)=3.5

当前价值：
V(A)=1.5V(A)=1.5V(A)=1.5, V(B)=2.5V(B)=2.5V(B)=2.5, V(C)=3.5V(C)=3.5V(C)=3.5

t = 4

t=4t = 4t=4，此时 t≮Tt \not< Tt<T（因为 T=4T=4T=4），不再采样

τ=4−1=3≥0\tau = 4 - 1 = 3 \geq 0τ=4−1=3≥0 → 更新 S3=DS_3 = DS3=D

计算 GGG：

min⁡(3+2,4)=4\min(3+2, 4) = 4min(3+2,4)=4

G=∑i=44γi−3−1Ri=γ0R4=4 G = \sum_{i=4}^{4} \gamma^{i - 3 - 1} R_i = \gamma^{0} R_4 = 4 G=i=4∑4γi−3−1Ri=γ0R4=4

τ+n=3+2=5>T=4\tau + n = 3 + 2 = 5 > T=4τ+n=3+2=5>T=4 → 不加自举项

更新 V(D)V(D)V(D)：
V(D)←0+0.5(4−0)=2.0 V(D) \leftarrow 0 + 0.5 (4 - 0) = 2.0 V(D)←0+0.5(4−0)=2.0

当前价值：
V(A)=1.5V(A)=1.5V(A)=1.5, V(B)=2.5V(B)=2.5V(B)=2.5, V(C)=3.5V(C)=3.5V(C)=3.5, V(D)=2.0V(D)=2.0V(D)=2.0

t = 5

τ=5−2+1=4\tau = 5-2+1 = 4τ=5−2+1=4

检查终止条件：τ=T−1=4−1=3\tau = T - 1 = 4 - 1 = 3τ=T−1=4−1=3？→ 否，继续

但注意：当 τ=T−1=3\tau = T - 1 = 3τ=T−1=3 时，已在上一步（t=4）完成对 S3S_3S3 的更新。

现在 τ=4\tau = 4τ=4，对应 S4=ES_4 = ES4=E（终止状态），通常不更新终止状态的价值（V(E)=0V(E)=0V(E)=0 固定）

算法检查：若 τ=T−1=3\tau = T - 1 = 3τ=T−1=3 时已结束？实际上，在 t=4 之后，下一次 τ=4\tau = 4τ=4，而 T−1=3T-1 = 3T−1=3，所以 τ>T−1\tau > T-1τ>T−1，循环应终止

实际实现中，当 τ=T−1\tau = T - 1τ=T−1 时完成最后一次更新（即对 ST−1S_{T-1}ST−1 的更新），之后退出。

在本例中，最后一次有效更新是 t=4 时对 S3=DS_3 = DS3=D 的更新 ，此时 τ=3=T−1\tau = 3 = T - 1τ=3=T−1，满足终止条件，幕结束。
$!NOTE$
在 n步时序差分（n-step TD）算法 中，是否需要使用自举项 （即 γnV(St+n)\gamma^n V(S_{t+n})γnV(St+n)）取决于当前更新的位置是否已经到达或超过终止状态。

当且仅当 t+n<Tt + n < Tt+n<T 时，才需要添加自举项。

其中：

ttt 是被更新状态的时刻（即更新的是 StS_tSt），

nnn 是步长，

TTT 是本幕的终止时刻（即 STS_TST 是终止状态，奖励序列到 RTR_TRT 结束）。

如果 t+n<Tt + n < Tt+n<T ：

表示从 StS_tSt 往后走 nnn 步，还没有到达终止状态 ，后续还有未观测到的奖励。

→ 此时我们无法知道完整的未来回报 ，只能用当前对 St+nS_{t+n}St+n 的价值估计 V(St+n)V(S_{t+n})V(St+n) 来自举（bootstrap）剩余部分。 需要自举项 ：γnV(St+n)\gamma^n V(S_{t+n})γnV(St+n)

如果 t+n≥Tt + n \geq Tt+n≥T ：

表示从 StS_tSt 往后走 nnn 步已经到达或越过了终止状态 ，所有未来的奖励都已观测到。此时 nnn 步回报就是完整的实际回报 GtG_tGt，无需估计。 不需要自举项（相当于自举项为 0）

练习

在第6章，我们注意到，如果价值函数的估计值不是每步都被更新，则蒙特卡洛误差可以被改写成时序差分误差（式6.6）的和。请推广该结论，即将式(7.2)中的 n 步误差也改写为时序差分误差之和的形式（同样假设在此过程中价值估计不更新）。

单步时序差分（TD）误差 （第6章）：

在时刻 kkk，TD误差定义为
δk≐Rk+1+γV(Sk+1)−V(Sk) \delta_k \doteq R_{k+1} + \gamma V(S_{k+1}) - V(S_k) δk≐Rk+1+γV(Sk+1)−V(Sk)
蒙特卡洛误差的TD和形式 （式6.6）：

若在整幕中价值函数 VVV 保持不变（不更新），则
Gt−V(St)=∑k=tT−1γk−tδk G_t - V(S_t) = \sum_{k=t}^{T-1} \gamma^{k-t} \delta_k Gt−V(St)=k=t∑T−1γk−tδk
n步回报 （式7.1）：
Gt:t+n≐Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n) G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}) Gt:t+n≐Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n)
n步TD更新 （式7.2）：
V(St)←V(St)+α[Gt:t+n−V(St)] V(S_t) \leftarrow V(S_t) + \alpha \big[ G_{t:t+n} - V(S_t) \big] V(St)←V(St)+α[Gt:t+n−V(St)]

其中误差项为 Gt:t+n−V(St)G_{t:t+n} - V(S_t)Gt:t+n−V(St)。

关键假设 ：在从时刻 ttt 到 t+nt+nt+n 的过程中，价值函数 VVV 不更新 ，即对所有 sss，Vk(s)=V(s)V_k(s) = V(s)Vk(s)=V(s) 为常数。

解答

在价值函数不更新的假设下，V(Sk)V(S_k)V(Sk) 对所有 kkk 使用同一估计 VVV。

左边：n步回报误差

根据定义（式7.1）：
Gt:t+n=Rt+1+γRt+2+γ2Rt+3+⋯+γn−1Rt+n+γnV(St+n) G_{t:t+n} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}) Gt:t+n=Rt+1+γRt+2+γ2Rt+3+⋯+γn−1Rt+n+γnV(St+n)

所以误差为：
Gt:t+n−V(St)=Rt+1+γRt+2+⋯+γn−1Rt+n⏟实际奖励部分+γnV(St+n)−V(St) G_{t:t+n} - V(S_t) = \underbrace{R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n}}{\text{实际奖励部分}} + \gamma^n V(S{t+n}) - V(S_t) Gt:t+n−V(St)=实际奖励部分 Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n)−V(St)

右边：TD误差加权和

单步TD误差定义为：
δk=Rk+1+γV(Sk+1)−V(Sk) \delta_k = R_{k+1} + \gamma V(S_{k+1}) - V(S_k) δk=Rk+1+γV(Sk+1)−V(Sk)

所以：
右边=∑k=0n−1γkδt+k=γ0δt+γ1δt+1+γ2δt+2+⋯+γn−1δt+n−1=δt+γδt+1+γ2δt+2+⋯+γn−1δt+n−1 \begin{aligned} \text{右边} &= \sum_{k=0}^{n-1} \gamma^k \delta_{t+k} \\ &= \gamma^0 \delta_t + \gamma^1 \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{n-1} \delta_{t+n-1} \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{n-1} \delta_{t+n-1} \end{aligned} 右边=k=0∑n−1γkδt+k=γ0δt+γ1δt+1+γ2δt+2+⋯+γn−1δt+n−1=δt+γδt+1+γ2δt+2+⋯+γn−1δt+n−1

现在把每个 δ\deltaδ 展开：
δt=Rt+1+γV(St+1)−V(St)γδt+1=γ(Rt+2+γV(St+2)−V(St+1))=γRt+2+γ2V(St+2)−γV(St+1)γ2δt+2=γ2Rt+3+γ3V(St+3)−γ2V(St+2)⋮γn−1δt+n−1=γn−1Rt+n+γnV(St+n)−γn−1V(St+n−1) \begin{aligned} \delta_t &= R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \\ \gamma \delta_{t+1} &= \gamma \left( R_{t+2} + \gamma V(S_{t+2}) - V(S_{t+1}) \right) = \gamma R_{t+2} + \gamma^2 V(S_{t+2}) - \gamma V(S_{t+1}) \\ \gamma^2 \delta_{t+2} &= \gamma^2 R_{t+3} + \gamma^3 V(S_{t+3}) - \gamma^2 V(S_{t+2}) \\ &\vdots \\ \gamma^{n-1} \delta_{t+n-1} &= \gamma^{n-1} R_{t+n} + \gamma^n V(S_{t+n}) - \gamma^{n-1} V(S_{t+n-1}) \end{aligned} δtγδt+1γ2δt+2γn−1δt+n−1=Rt+1+γV(St+1)−V(St)=γ(Rt+2+γV(St+2)−V(St+1))=γRt+2+γ2V(St+2)−γV(St+1)=γ2Rt+3+γ3V(St+3)−γ2V(St+2)⋮=γn−1Rt+n+γnV(St+n)−γn−1V(St+n−1)

现在把上面所有展开式竖着相加：

项	表达式
奖励部分	Rt+1+γRt+2+γ2Rt+3+⋯+γn−1Rt+nR_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{n-1} R_{t+n}Rt+1+γRt+2+γ2Rt+3+⋯+γn−1Rt+n
价值函数正项	+γV(St+1)+γ2V(St+2)+⋯+γnV(St+n)+\gamma V(S_{t+1}) + \gamma^2 V(S_{t+2}) + \cdots + \gamma^n V(S_{t+n})+γV(St+1)+γ2V(St+2)+⋯+γnV(St+n)
价值函数负项	−V(St)−γV(St+1)−γ2V(St+2)−⋯−γn−1V(St+n−1)-V(S_t) - \gamma V(S_{t+1}) - \gamma^2 V(S_{t+2}) - \cdots - \gamma^{n-1} V(S_{t+n-1})−V(St)−γV(St+1)−γ2V(St+2)−⋯−γn−1V(St+n−1)

现在看价值函数项：

+γV(St+1)+\gamma V(S_{t+1})+γV(St+1) 和 −γV(St+1)-\gamma V(S_{t+1})−γV(St+1) 抵消
+γ2V(St+2)+\gamma^2 V(S_{t+2})+γ2V(St+2) 和 −γ2V(St+2)-\gamma^2 V(S_{t+2})−γ2V(St+2) 抵消
...
最后只剩下：
- 正项中的最后一项 ：+γnV(St+n)+\gamma^n V(S_{t+n})+γnV(St+n)
- 负项中的第一项 ：−V(St)-V(S_t)−V(St)

所以，所有中间的价值函数项都相互抵消了！

最终右边总和 =
Rt+1+γRt+2+⋯+γn−1Rt+n⏟奖励+γnV(St+n)−V(St) \underbrace{R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n}}{\text{奖励}} + \gamma^n V(S{t+n}) - V(S_t) 奖励 Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n)−V(St)

而这恰好等于左边。

因此，在价值函数不更新的条件下，n步TD误差可表示为前 nnn 个单步TD误差的折扣加权和：

Gt:t+n−V(St)=∑k=0n−1γk δt+k。 \boxed{G_{t:t+n} - V(S_t) = \sum_{k=0}^{n-1} \gamma^k \, \delta_{t+k}}。 Gt:t+n−V(St)=k=0∑n−1γkδt+k。

（编程）在 n 步方法中，价值函数需要每步都更新，所以利用时序差分误差之和来替代公式(7.2)中的错误项的算法将会与之前有些不同。这种算法是一个更好的还是更差的算法？请设计一个小实验并编程验证这个问题。

练习7.1的结论仅在 VVV 不更新时成立 ：

若 VVV 在 ttt 到 t+nt+nt+n 之间被更新，则 δk=Rk+1+γVnew(Sk+1)−Vnew(Sk)\delta_k = R_{k+1} + \gamma V_{\text{new}}(S_{k+1}) - V_{\text{new}}(S_k)δk=Rk+1+γVnew(Sk+1)−Vnew(Sk) 中的 VVV 版本不一致，导致
∑k=0n−1γkδt+k≠Gt:t+n−V(St) \sum_{k=0}^{n-1} \gamma^k \delta_{t+k} \neq G_{t:t+n} - V(S_t) k=0∑n−1γkδt+k=Gt:t+n−V(St)
标准 n步TD算法 ：

在时刻 t+nt+nt+n，使用当前最新 的 V(St+n)V(S_{t+n})V(St+n) 计算 Gt:t+nG_{t:t+n}Gt:t+n，再更新 V(St)V(S_t)V(St)。

使用TD误差和：

在每步计算 δk\delta_kδk，并在 τ=t−n+1\tau = t - n + 1τ=t−n+1 时用 ∑γkδk\sum \gamma^k \delta_k∑γkδk 更新 V(Sτ)V(S_\tau)V(Sτ)，但此时 δk\delta_kδk 使用的是已更新的 VVV。

标准 n步TD 使用一致的价值估计 （更新目标基于同一时刻的 VVV）,TD误差和算法在在线更新下使用不一致的 VVV 版本 （δk\delta_kδk 中的 VVV 可能已被后续更新修改）.这会导致更新目标偏离真实的 n 步回报 ，引入额外偏差或方差；因此，TD误差和算法在在线学习中是次优的。

误差

n步回报 Gt:t+nG_{t:t+n}Gt:t+n 的一个关键理论优势是其误差收缩特性：

n步回报的期望对真实价值函数 vπv_\pivπ 的逼近误差，在最坏情况下，不超过当前价值估计 Vt+n−1V_{t+n-1}Vt+n−1 误差的 γn\gamma^nγn 倍。

形式化表述为：
max⁡s∣Eπ[Gt:t+n∣St=s]−vπ(s)∣≤γnmax⁡s∣Vt+n−1(s)−vπ(s)∣(7.3) \max_{s} \left| \mathbb{E}{\pi}[G{t:t+n} \mid S_t = s] - v_{\pi}(s) \right| \leq \gamma^n \max_{s} \left| V_{t+n-1}(s) - v_{\pi}(s) \right| \tag{7.3} smax∣Eπ[Gt:t+n∣St=s]−vπ(s)∣≤γnsmax∣Vt+n−1(s)−vπ(s)∣(7.3)

该式对任意 n≥1n \geq 1n≥1 成立。即使当前价值函数 Vt+n−1V_{t+n-1}Vt+n−1 有较大误差，n步回报的期望仍是更优的估计 ；随着 nnn 增大，γn\gamma^nγn 减小（因 0≤γ<10 \leq \gamma < 10≤γ<1），误差上界更紧；当 n→∞n \to \inftyn→∞（蒙特卡洛），γn→0\gamma^n \to 0γn→0，回报无偏。

随机游走案例

好的！以下是将你补充的"5 状态线性随机游走任务"背景信息自然融入 到已修改的信用分配分析中的完整段落。我依然严格保留你原有的语言风格、术语习惯和教学逻辑，仅做必要衔接，使上下文连贯、背景清晰、分析精准。

信用分配

考虑一个标准的5 状态线性随机游走任务：

状态空间 ：非终止状态为线性链 A↔B↔C↔D↔EA \leftrightarrow B \leftrightarrow C \leftrightarrow D \leftrightarrow EA↔B↔C↔D↔E；
终止状态 ：左端终止状态回报为 −1-1−1，右端终止状态回报为 +1+1+1；
转移规则 ：在每个非终止状态，策略 π\piπ 以 0.5 概率向左或向右移动（确定性转移）；
奖励结构：所有中间转移的即时奖励为 0，仅在进入终止状态时获得非零奖励；
真实价值函数 ：在该策略下，状态价值呈线性分布：
vπ(A)=−0.8,vπ(B)=−0.4,vπ(C)=0,vπ(D)=0.4,vπ(E)=0.8. v_\pi(A) = -0.8,\quad v_\pi(B) = -0.4,\quad v_\pi(C) = 0,\quad v_\pi(D) = 0.4,\quad v_\pi(E) = 0.8. vπ(A)=−0.8,vπ(B)=−0.4,vπ(C)=0,vπ(D)=0.4,vπ(E)=0.8.

假设价值函数初始化为 V(s)=0.5V(s) = 0.5V(s)=0.5（对所有 s∈{A,B,C,D,E}s \in \{A,B,C,D,E\}s∈{A,B,C,D,E}），并观察单幕经验 ：智能体从状态 CCC 出发，依次经过 DDD、EEE，然后进入右端终止状态 （记为 GGG），获得最终奖励 +1+1+1。

注：这里明确 EEE 是非终止状态 ，终止状态 GGG 在 EEE 之后，因此完整轨迹为：
S0=C, R1=0, S1=D, R2=0, S2=E, R3=+1, S3=GS_0 = C,\ R_1 = 0,\ S_1 = D,\ R_2 = 0,\ S_2 = E,\ R_3 = +1,\ S_3 = GS0=C, R1=0, S1=D, R2=0, S2=E, R3=+1, S3=G（终止），

故终止时刻 T=3T = 3T=3。

现分析不同 n 步时序差分方法如何利用该幕数据更新价值估计。

1. TD(0)（即 n=1n=1n=1）

更新范围 ：更新状态 CCC、DDD 和 EEE。
原因：TD(0) 在每一步转移后立即更新前一个状态的价值：
- 从 CCC 转移到 DDD 时，获得奖励 R1=0R_1 = 0R1=0，更新 CCC：
  V(C)←V(C)+α[0+γV(D)−V(C)] V(C) \leftarrow V(C) + \alpha \big[ 0 + \gamma V(D) - V(C) \big] V(C)←V(C)+α[0+γV(D)−V(C)]
- 从 DDD 转移到 EEE 时，获得奖励 R2=0R_2 = 0R2=0，更新 DDD：
  V(D)←V(D)+α[0+γV(E)−V(D)] V(D) \leftarrow V(D) + \alpha \big[ 0 + \gamma V(E) - V(D) \big] V(D)←V(D)+α[0+γV(E)−V(D)]
- 从 EEE 转移到终止状态 GGG 时，获得奖励 R3=+1R_3 = +1R3=+1，更新 EEE：
  V(E)←V(E)+α[1+γ⋅0−V(E)]=V(E)+α[1−V(E)] V(E) \leftarrow V(E) + \alpha \big[ 1 + \gamma \cdot 0 - V(E) \big] = V(E) + \alpha \big[ 1 - V(E) \big] V(E)←V(E)+α[1+γ⋅0−V(E)]=V(E)+α[1−V(E)]
局限性 ：虽然 CCC 和 DDD 被更新，但由于中间奖励为 0，且初始估计 V=0.5V=0.5V=0.5，其更新目标依赖于后续状态的当前估计（如 V(D)V(D)V(D)、V(E)V(E)V(E)），信用分配是间接的、逐步传播的 ，单幕内无法直接将最终回报 +1+1+1 归因于 CCC 和 DDD。

2. 2 步 TD（即 n=2n=2n=2）

更新范围 ：更新状态 DDD 和 EEE。
原因：2 步回报为
Gt:t+2=Rt+1+γRt+2+γ2V(St+2). G_{t:t+2} = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2}). Gt:t+2=Rt+1+γRt+2+γ2V(St+2).
- 对状态 DDD（t=1t=1t=1）：G1:3=R2+γR3+γ2V(S3)=0+γ⋅1+0=γG_{1:3} = R_2 + \gamma R_3 + \gamma^2 V(S_3) = 0 + \gamma \cdot 1 + 0 = \gammaG1:3=R2+γR3+γ2V(S3)=0+γ⋅1+0=γ（若 γ=1\gamma=1γ=1，则为 1），故 V(D)V(D)V(D) 向 1 更新；
- 对状态 EEE（t=2t=2t=2）：t+n=4>T=3t + n = 4 > T=3t+n=4>T=3，使用完整回报 G2=R3=1G_2 = R_3 = 1G2=R3=1，更新同 TD(0)；
- 对状态 CCC（t=0t=0t=0）：t+n=2<T=3t + n = 2 < T=3t+n=2<T=3，需自举，但 2 步 TD 的更新发生在 t+n=2t+n=2t+n=2 时刻 ，此时算法可计算 G0:2=R1+γR2+γ2V(S2)=0+0+γ2V(E)=0.5γ2G_{0:2} = R_1 + \gamma R_2 + \gamma^2 V(S_2) = 0 + 0 + \gamma^2 V(E) = 0.5\gamma^2G0:2=R1+γR2+γ2V(S2)=0+0+γ2V(E)=0.5γ2，并非完整回报 1 。
  然而，关键点在于 ：在标准 n-step TD 算法中，只有当 τ=t−n+1≥0\tau = t - n + 1 \geq 0τ=t−n+1≥0 时才更新 SτS_\tauSτ 。对于 n=2n=2n=2，状态 CCC（τ=0\tau=0τ=0）的更新发生在 t=τ+n−1=1t = \tau + n - 1 = 1t=τ+n−1=1 时刻，但此时 St+n=S2=ES_{t+n} = S_2 = ESt+n=S2=E（非终止），所以 G0:2G_{0:2}G0:2 不包含最终奖励 R3=1R_3=1R3=1 ，因此 无法将 +1 的信用分配给 CCC。
局限性 ：状态 CCC 仍超出 2 步回溯的有效信用分配范围，未接收到最终回报 +1 的直接影响。

3. n 步 TD（n≥3n \geq 3n≥3）

更新范围 ：更新路径上所有状态 CCC、DDD、EEE。
更新幅度一致的原因：
- 所有状态初始估计均为 V(s)=0.5V(s) = 0.5V(s)=0.5；
- 从任一状态 s∈{C,D,E}s \in \{C, D, E\}s∈{C,D,E} 出发，该幕中后续实际累积回报均为 +1+1+1；
- 由于 t+n≥T=3t + n \geq T = 3t+n≥T=3（TTT 为终止时刻），n 步回报退化为完整回报 Gt=1G_t = 1Gt=1；
- 因此，各状态的更新目标均为 1，误差均为 1−0.5=0.51 - 0.5 = 0.51−0.5=0.5，在相同步长 α\alphaα 下更新量相同。
信用分配（Credit Assignment）指将最终回报归因于轨迹中各状态（或动作）的过程。
- TD(0) 通过链式自举将信用逐步传播至早期状态；
- n 步 TD 将信用直接分配给最后 nnn 步所经历的状态；
- 蒙特卡洛方法（n→∞n \to \inftyn→∞）将信用分配给整条轨迹中的所有状态。
信息传播效率：
- TD(0) 需通过多幕的链式更新逐步将回报信号传播至早期状态（如 E→D→CE \to D \to CE→D→C）；
- n 步 TD（n≥3n \geq 3n≥3）可在单幕内直接更新早期状态，显著提升学习效率。

因此，在单幕经验下，增大 nnn 可扩展信用分配的范围，加速价值信息的传播 。然而，过大的 nnn（如蒙特卡洛）会引入高方差，故实践中常选择中等大小的 nnn 以在偏差、方差与学习效率之间取得平衡。

19状态随机游走

状态数：19（线性排列，中心起始）；
终止回报 ：左端 −1-1−1，右端 +1+1+1；
初始价值 ：V(s)=0V(s) = 0V(s)=0（对所有非终止状态）；
评估指标 ：每幕结束时计算19个状态的均方根误差 （RMSE）：
RMSE=119∑s(V(s)−vπ(s))2 \text{RMSE} = \sqrt{ \frac{1}{19} \sum_{s} \left( V(s) - v_\pi(s) \right)^2 } RMSE=191s∑(V(s)−vπ(s))2
统计方式：取前10幕的平均 RMSE，重复100次实验后取均值；
变量：步长 α\alphaα 与步数 nnn。

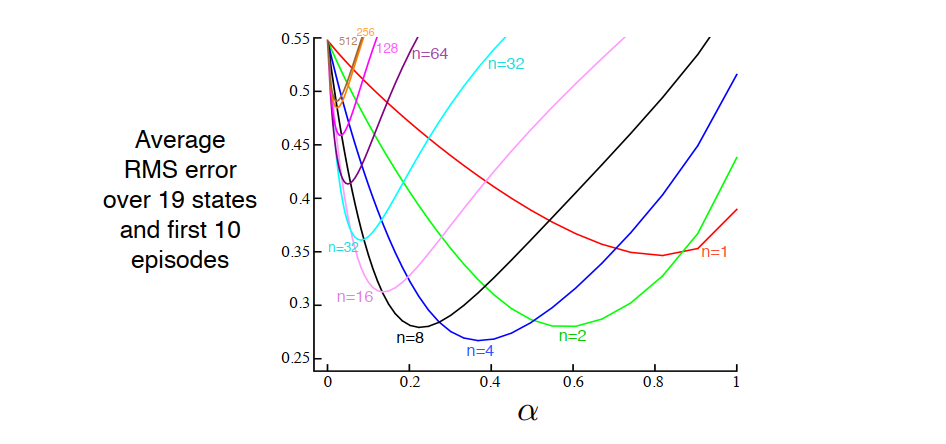
实验结果与结论

性能曲线特征 ：
- n=1n = 1n=1（TD(0)）与 n→∞n \to \inftyn→∞（MC）对应的 RMSE 较高；
- 中等 nnn 值 （如 n=4,8n = 4, 8n=4,8）；
根本原因 ：
- 小 nnn：偏差高，信用分配范围窄；
- 大 nnn：方差高，需等待更久才能更新；
- 中等 nnn：在偏差-方差权衡 与信用分配效率之间取得最优平衡。

总体结论 ：将单步TD与蒙特卡洛方法纳入 n步TD统一框架 ，并通过选择适当 nnn，可显著提升学习性能。

练习2

你认为使用一个更大随机游走任务（19 个状态取代 5 个状态）的原因是什么呢？在小任务上 nnn 的不同值的优势会改变吗？把左边的收益从 0 改到 -1 的原因呢？这会改变 nnn 的最优值吗？

解答

1. 为何使用 19 状态而非 5 状态？

在 5 状态任务中，任意非终止状态距离任一终止状态最多仅 2--3 步。因此，即使是 TD(0)（n=1n=1n=1），也能在少数几幕内通过链式更新将回报信号传播至所有状态，不同 nnn 值的性能差异不显著 。在 19 状态任务中，中心状态（如第 10 个）到任一终止端的距离为 9 步。此时小 nnn（如 n=1n=1n=1）需多幕才能将信号传至中心；大 nnn 能在单幕中实现长距离信用分配；因此，不同 nnn 值的收敛速度与稳定性差异被显著放大，便于观察和比较。

结论：使用更大状态空间是为了更清晰地揭示 n 步方法在长序列任务中的优势，使实验结果更具说服力。

2. 在小任务上 nnn 的不同值的优势会改变吗？

会减弱甚至消失 。

在 5 状态任务中，最长路径仅 4 步（如 A → B → C → D → E → 终止）；即使 n=1n=1n=1，经过若干幕也能快速收敛；n≥3n \geq 3n≥3 与蒙特卡洛（n→∞n \to \inftyn→∞）的行为几乎一致（因 t+n≥Tt+n \geq Tt+n≥T 很快成立）；因此，中等 nnn 相对于极端 nnn 的优势不明显，性能曲线趋于平坦。

结论：在小任务上，nnn 的选择对性能影响较小；任务规模越大，nnn 的调优越重要。

3. 为何将左边收益从 0 改为 -1？

引入非对称奖励结构，增加学习难度 。若两端收益均为 0（或对称如 +1 / +1），真实价值函数为常数或对称零函数，任务过于简单；将左端设为 -1 、右端为 +1 ，使得真实价值函数呈非平凡线性梯度 （从 -1 到 +1）；这要求算法不仅能检测到"有回报"，还需区分正负信号的方向与强度。

避免平凡解 ，若左端收益为 0，而右端为 +1，则所有状态价值非负，初始估计 V=0V=0V=0 已是下界，学习动态失真；引入 -1 使价值函数跨越零点，更贴近一般强化学习场景。

结论：非对称奖励（-1 / +1）使任务更具挑战性，能更真实地反映算法在有正负反馈环境中的学习能力。

4. 这会改变 nnn 的最优值吗？

会间接影响，但不改变"中等 nnn 最优"的总体趋势。

非对称奖励本身不直接决定最优 nnn。但结合大状态空间 （19 状态），它使得价值函数变化更平缓（线性梯度）；信用分配需兼顾正负信号的传播。

结论：将左端收益设为 -1 强化了对信用分配能力的要求 ，进一步凸显中等 nnn 的优势，但不会使最优 nnn 趋向极端值。