1. 多维数组
python
>>> import numpy as np
>>> A = np.array([1,2,3,4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)
1
>>> A.shape
(4,)
>>> A.shape[0]
4
>>>np.dim(A) 数组的维数
A.shape 数组的形状,结果是个元组(tuple)。 例如,二维数组时返回的
是元组 (4,3),三维数组时返回的是元组(4,3,2),因此一维数组时也同样以
元组的形式返回结果。
bash
>>> B = np.array([[1,2],[3,4],[5,6]])
>>> print(B)
[[1 2]
[3 4]
[5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)
>>> B
array([[1, 2],
[3, 4],
[5, 6]])
>>>这里生成了一个3 × 2的数组B。 3 × 2的数组表示第一个维度有3个元素,
第二个维度有2个元素。另外,第一个维度对应第0维,第二个维度对应第
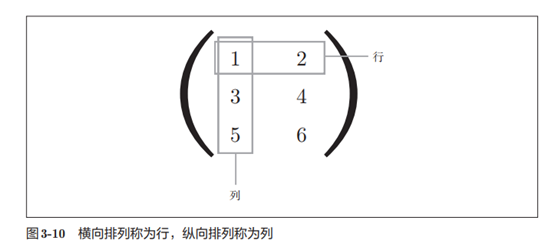
1维(Python的索引从0开始)。二维数组也称为矩阵(matrix)。如图3-10所示,
数组的横向排列称为行(row),纵向排列称为列(column)。
2.矩阵乘法
下面,我们来介绍矩阵(二维数组)的乘积。比如2 × 2的矩阵,其乘积
可以像图3-11这样进行计算(按图中顺序进行计算是规定好了的)
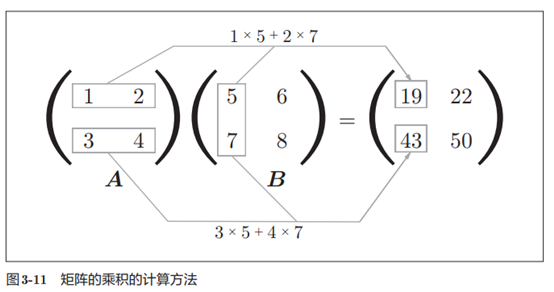
矩阵的乘积是通过左边矩阵的行(横向)和右边矩阵的列(纵
向)以对应元素的方式相乘后再求和而得到的。并且,运算的结果保存为新
的多维数组的元素。比如, A的第1行和B的第1列的乘积结果是新数组的
第1行第1列的元素, A的第2行和B的第1列的结果是新数组的第2行第1
列的元素。另外,在本书的数学标记中,矩阵将用黑斜体表示(比如,矩阵
A),以区别于单个元素的标量(比如, a或b)。这个运算在Python中可以用
如下代码实现。
bash
>>> A = np.array([[1,2],[3,4]])
>>> A.shape
(2, 2)
>>> B = np.array([[5,6],[7,8]])
>>> B.shape
(2, 2)
>>> np.dot(A,B)
array([[19, 22],
[43, 50]])
>>> 这 里, A 和 B 都 是 2 × 2 的 矩 阵,它 们 的 乘 积 可 以 通 过 NumPy 的
np.dot()函数计算(乘积也称为点积)。 np.dot()接收两个NumPy数组作为参
数,并返回数组的乘积。这里要注意的是, np.dot(A, B)和 np.dot(B, A)的
值可能不一样。和一般的运算(+或*等)不同,矩阵的乘积运算中,操作数(A、
B)的顺序不同,结果也会不同。
bash
>>> A = np.array([[1,2,3],[4,5,6]])
>>> A.shape
(2, 3)
>>> B = np.array([[1,2],[3,4],[5,6]])
>>> B.shape
(3, 2)
>>> np.dot(A,B)
array([[22, 28],
[49, 64]])
>>>2 × 3的矩阵A和3 × 2的矩阵B的乘积可按以上方式实现。这里需要
注意的是矩阵的形状(shape)。具体地讲,矩阵A的第1维的元素个数(列数)
必须和矩阵B的第0维的元素个数(行数)相等。在上面的例子中,矩阵A
的形状是2 × 3,矩阵B的形状是3 × 2,矩阵A的第1维的元素个数(3)和
矩阵B的第0维的元素个数(3)相等。如果这两个值不相等,则无法计算矩
阵的乘积。比如,如果用Python计算2 × 3 的矩阵A和2 × 2的矩阵C的乘
积,则会输出如下错误。
bash
>>> C = np.array([[1,2],[3,4]])
>>> C.shape
(2, 2)
>>> np.dot(A,C)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)
>>>这个错误的意思是,矩阵A的第1维和矩阵C的第0维的元素个数不一
致(维度的索引从0开始)。也就是说,在多维数组的乘积运算中,必须使两
个矩阵中的对应维度的元素个数一致,这一点很重要。我们通过图3-12再来
确认一下。
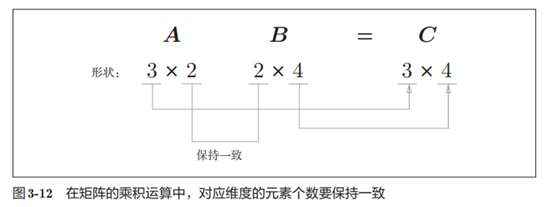
图3-12中, 3 × 2的矩阵A和2 × 4 的矩阵B的乘积运算生成了3 × 4的
矩阵C。如图所示,矩阵A和矩阵B的对应维度的元素个数必须保持一致。
此外,还有一点很重要,就是运算结果的矩阵C的形状是由矩阵A的行数
和矩阵B的列数构成的。
当A是二维矩阵、 B是一维数组时
bash
>>> A = np.array([[1,2],[3,4],[5,6]])
>>> A.shape
(3, 2)
>>> B = np.array([7,8])
>>> B.shape
(2,)
>>> np.dot(A,B)
array([23, 53, 83])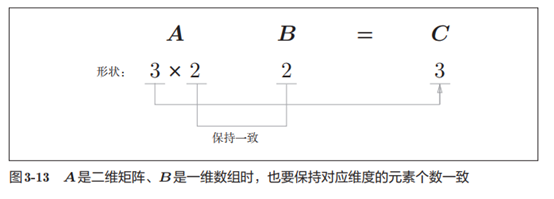
3.神经网络的内积
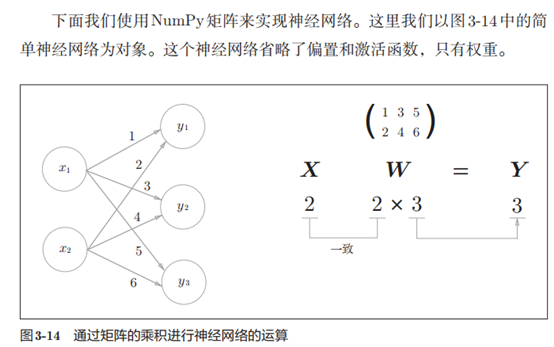
bash
>>> X = np.array([1,2])
>>> X.shape
(2,)
>>> W = np.array([[1,3,5],[2,4,6]])
>>> print(W)
[[1 3 5]
[2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X,W)
>>> print(Y)
[ 5 11 17]如上所示,使用np.dot(多维数组的点积),可以一次性计算出Y 的结果。
这意味着,即便Y 的元素个数为100或1000,也可以通过一次运算就计算出
结果!如果不使用np.dot,就必须单独计算Y 的每一个元素(或者说必须使
用for语句),非常麻烦。因此,通过矩阵的乘积一次性完成计算的技巧,在
实现的层面上可以说是非常重要的。