文章目录
- 背景
- 目标
- Pre准备
- [1,Introduction and coding our first neuron 编写第一个神经元](#1,Introduction and coding our first neuron 编写第一个神经元)
-
- 张量运算
- [NumPy 乘法及深度学习常用矩阵运算](#NumPy 乘法及深度学习常用矩阵运算)
- [2,Coding a layer of neurons 编写神经元层](#2,Coding a layer of neurons 编写神经元层)
- [3,Hidden layer activation functions 隐藏层激活函数](#3,Hidden layer activation functions 隐藏层激活函数)
- [4,Output layer activation function 输出层激活函数](#4,Output layer activation function 输出层激活函数)
-
- softmax
- [overflow prevention 溢出预防](#overflow prevention 溢出预防)
- [5,Calculating and implementing loss 计算并实现损失](#5,Calculating and implementing loss 计算并实现损失)
-
- 计算三张图像批次的损失
-
- step1:先明确「维度结构」
- step2:按「索引类型」分类记忆
- 明确两个完全不同的索引逻辑
- [什么时候是 zip,什么时候是笛卡尔积?](#什么时候是 zip,什么时候是笛卡尔积?)
- [6,Backpropogation 反向传播](#6,Backpropogation 反向传播)
-
-
- [1. 导数的两种核心用途:针对"参数" vs 针对"输入"](#1. 导数的两种核心用途:针对“参数” vs 针对“输入”)
- [2. 反向传播的核心操作:损失函数导数 + 链式法则](#2. 反向传播的核心操作:损失函数导数 + 链式法则)
- [3. 反向传播的本质:"反向递推"的逻辑](#3. 反向传播的本质:“反向递推”的逻辑)
- 两个梯度:参数梯度与输入梯度
-
- [7,Optimizers 优化器](#7,Optimizers 优化器)
- [8,Learning rate and momentum 学习率和动量](#8,Learning rate and momentum 学习率和动量)
- [9,Complete Neural Network from scratch 从头开始构建完整的神经网络](#9,Complete Neural Network from scratch 从头开始构建完整的神经网络)
- 10,只使用Numpy构建的1个简单全连接网络全代码
-
- 真纯Numpy手搓1个简单的神经网络
- 一些推导中需要注意的地方
- 为什么要合并softmax和多分类交叉熵损失?
- 梯度爆炸与梯度消失
-
- 梯度消失(vanishing)
- 梯度爆炸(exploding)
- 解决方法
- 一些题外话
-
- 首先是数学符号说明,都是一些微积分中简单的符号
- [梯度消失与Dead Neuron、Dropout等](#梯度消失与Dead Neuron、Dropout等)
-
- [梯度消失 ↔ Dead Neuron:"因" 与 "果" 的关系](#梯度消失 ↔ Dead Neuron:“因” 与 “果” 的关系)
- [Dropout ↔ 梯度消失 / Dead Neuron:"缓解工具" 与 "问题" 的关系](#Dropout ↔ 梯度消失 / Dead Neuron:“缓解工具” 与 “问题” 的关系)
- 为什么要修正动量偏差?
-
- [1. 原始公式(θ=θ−η⋅∇L):"只看脚下,步长固定"](#1. 原始公式(θ=θ−η⋅∇L):“只看脚下,步长固定”)
- [2. 动量(对应代码里的weight_momentums):"加上惯性,走得更稳更快"](#2. 动量(对应代码里的weight_momentums):“加上惯性,走得更稳更快”)
- 3,自适应学习率的问题
- [4. 缓存(对应代码里的weight_cache):"看之前的步长,灵活调整迈腿大小"](#4. 缓存(对应代码里的weight_cache):“看之前的步长,灵活调整迈腿大小”)
- 三者的逻辑关系(对比表)
- 11,检查一下nnfs
背景
这个系列其实是当初和鱼书一起刷的,但是鱼书我很早就停了更新推文。
考虑到这个系列其实是AI4S非常典型的教程系列,而且是正经的为所有研究蛋白质、蛋白质组学、蛋白质模型的新手准备的一个AI4S的教程,所以开这个新坑。
最最最最最重要的是,最近才发现Colab在Vscode出了extension,是官方的拓展!不是之前开源社区的各种工具。
Google 在微软官方 Jupyter Extension 基础上开发了 Colab VS Code Extension 扩展,Colab Extension 通过 Kernel 选项将 Notebook 的执行交给 Colab Server。
详情可以参考我之前的博客:在vscode中使用colab的GPU算力
另外文件系统挂载的问题其实已经解决了,参考https://github.com/googlecolab/colab-vscode/issues/300#issuecomment-3689252902
目标

Pre准备
因为是在colab上实验的
python
!nvidia-smi
导入该库的一些数据、一些函数,都封装在了一个库中:nnfs
python
# package for creating our dataset
!pip install nnfs
python
import numpy as np
import nnfs
from nnfs.datasets import spiral_data
import matplotlib.pyplot as plt
import math
nnfs.init()这里的nnfs就是我们后续处理的一切数据基础,是一个module

1,Introduction and coding our first neuron 编写第一个神经元

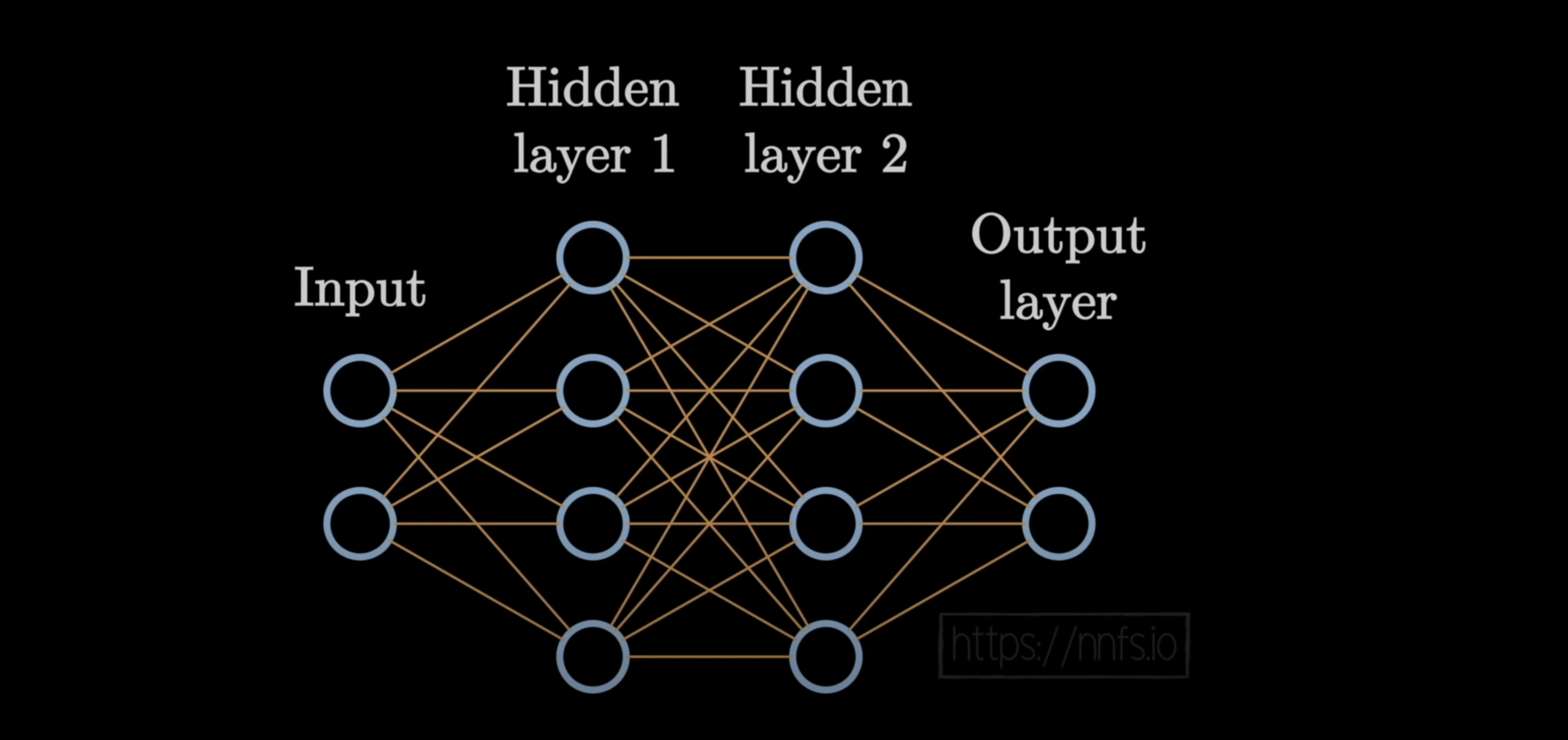


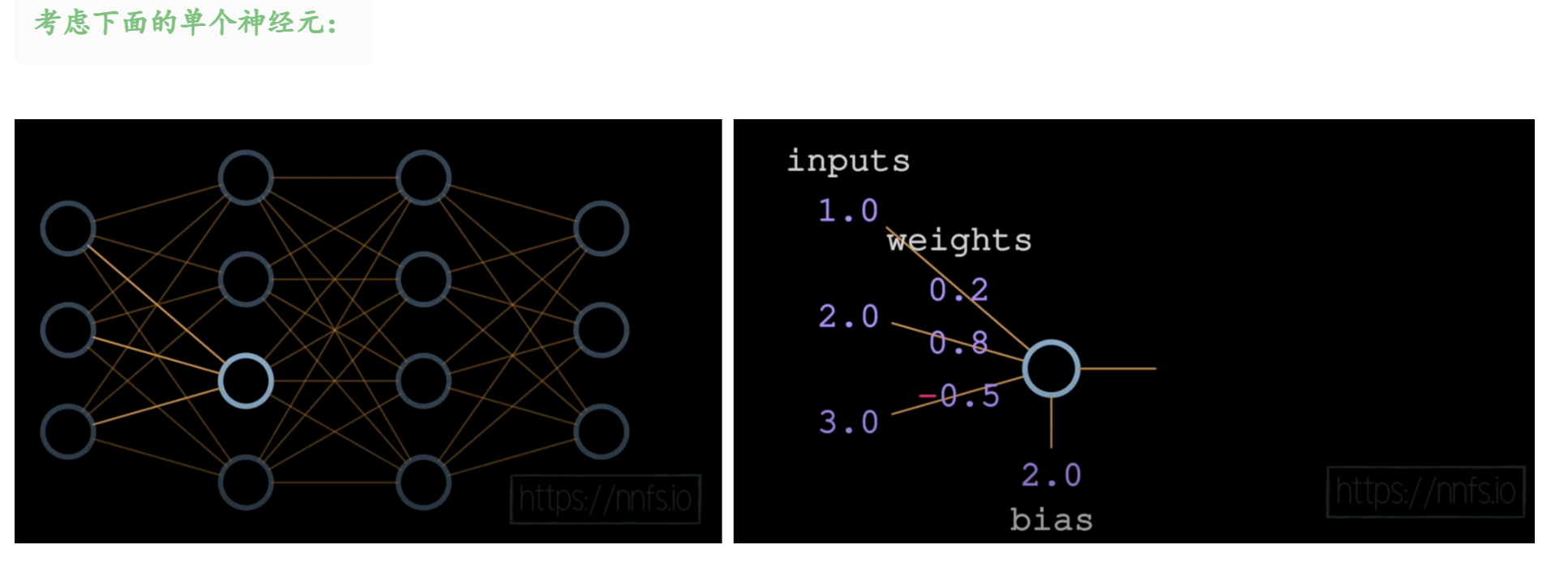
让我们计算前一层(有 3 个神经元)的输出:

但是这两个神经元都是(3,),也就是说明 inputs 和 weights 都是一维数组,不是严格的二维矩阵。
张量运算
这里提一下深度学习里的张量运算:

张量维度是运算的前提:
深度学习框架(如 TensorFlow/PyTorch)和 NumPy 的矩阵乘法,都要求维度匹配(前一个矩阵的列数 = 后一个矩阵的行数)。
先总结一些深度学习常用矩阵运算,比如说画成1个列表,需要牢记:
| 运算类型 | 符号 / 函数 | 作用 | 代码示例 | 输出结果 | 深度学习场景 |
|---|---|---|---|---|---|
| 矩阵乘法 | @ / np.matmul() |
线性变换核心,满足 前阵列数 = 后阵行数 | inputs @ weights |
[[0.3]] |
全连接层 z = X @ W + b |
| 点积 | np.dot() |
一维向量内积;二维等价于 np.matmul |
np.dot(inputs, weights) |
[[0.3]] |
向量相似度、注意力得分 |
| 逐元素乘法 | * |
对应位置相乘,触发广播 | inputs * weights |
[[0.2, 0.4, 0.6], [0.8, 1.6, 2.4], [-0.5, -1.0, -1.5]] |
注意力权重加权、元素级更新 |
| 广播加法 | + |
标量 / 向量与矩阵自动扩展相加 | (inputs @ weights) + bias |
[[2.3]] |
偏置项添加(z = X@W + b ) |
| 矩阵转置 | .T |
行列互换,调整维度顺序 | weights.T |
[[0.2, 0.8, -0.5]] |
维度适配、矩阵逆运算前置 |
| 元素级激活(ReLU) | np.maximum(x, 0) |
引入非线性,过滤负值 | np.maximum(inputs @ weights, 0) |
[[0.3]] |
隐藏层激活函数 |
| 元素级激活(Sigmoid) | 1/(1+np.exp(-x)) |
输出映射到 (0,1) | 1/(1+np.exp(-(inputs @ weights + bias))) |
[[0.9102]] |
二分类输出层 |
| 矩阵求和 | np.sum() |
降维,计算元素总和 | np.sum(inputs) |
6.0 |
损失函数计算、池化简化 |
| 矩阵求均值 | np.mean() |
降维,计算元素均值 | np.mean(inputs) |
2.0 |
数据归一化、批归一化 |
| 批量矩阵乘法 | np.matmul() |
多组样本同时运算 | inputs_batch = np.array([[1,2,3], [4,5,6]]) inputs_batch @ weights |
[[0.3], [1.1]]</font> |
批量处理样本(batch_size × in_dim ) |
NumPy 乘法及深度学习常用矩阵运算
假设我们完全没有深度学习的基础,只有线性代数的直觉+一点numpy运算基础,我们会reshape
python
inputs = np.asarray([1.0, 2.0, 3.0])
weights = np.asarray([0.2, 0.8, -0.5])
bias = 2.0
# 输出应该是1x3(1行3列)x 3x1(3行1列)+ bias
print(inputs.shape, weights.shape)
# 应该先转化一下shape
inputs = inputs.reshape(1,3)
weights = weights.reshape(3,1)
# 再看一下
print(inputs.shape, weights.shape)
outputs = inputs * weights + bias
print(outputs)
但是符号不能想当然!我们标量运算中的符号确实是乘法,但在数组也就是张量运算中却是逐元素乘法。
所以上面其实是做的一个最基础的逐元素乘法,也是numpy中基础知识:
规则是 两个数组的形状能通过广播匹配,它不会做矩阵乘法,而是把两个数组的元素逐个相乘。
在我们的代码里:

简单的算一下就知道了:
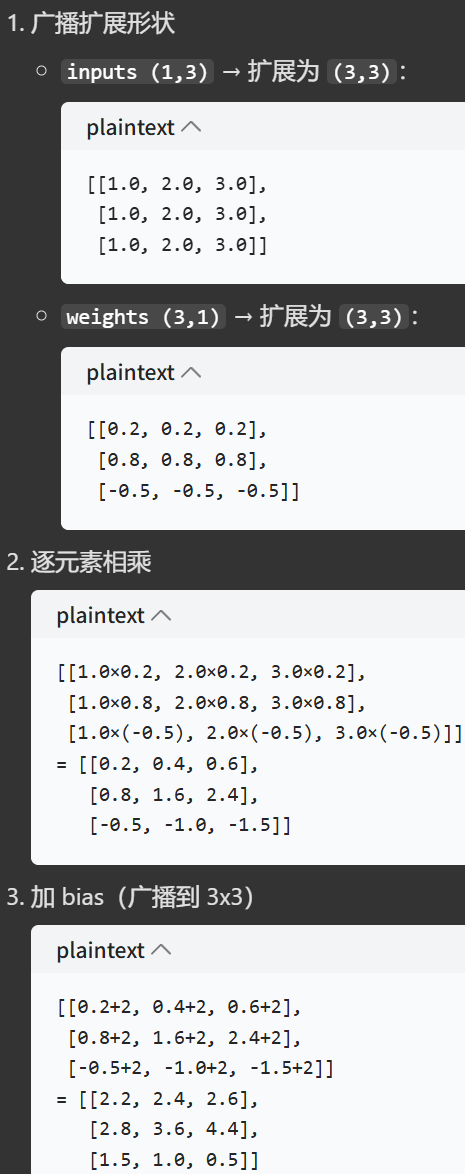
1个核心乘法类型对照表(逐元素 / 矩阵 / 点积):
| 运算类型 | 运算符 / 函数 | 语法示例 | 形状变化 | 计算逻辑 | 输出结果(示例) | 适用场景 |
|---|---|---|---|---|---|---|
| 逐元素乘法 | * |
inputs_1x3 * weights_3x1 |
(1,3) × (3,1) → (3,3) |
触发广播,两个数组都扩展为(3,3) 后对应位置相乘 |
[[0.2, 0.4, 0.6], [0.8, 1.6, 2.4], [-0.5, -1.0, -1.5]] |
同形状数组元素级操作,深度学习中权重元素级更新 |
| 矩阵乘法 | @ 或 np.matmul() |
inputs_1x3 @ weights_3x1 np.matmul(inputs_1x3, weights_3x1) |
(1,3) × (3,1) → (1,1) |
严格遵循矩阵乘法规则:前阵列数 = 后阵行数 | [[0.3]] |
深度学习全连接层、线性变换的核心运算 |
| 点积 | np.dot() |
np.dot(inputs_1x3, weights_3x1) |
(1,3) × (3,1) → (1,1) |
一维数组返回标量;二维数组等价于np.matmul |
[[0.3]] |
向量内积计算、相似度度量 |
所以我们这里应该改成@符号
plain
inputs = np.asarray([1.0, 2.0, 3.0])
weights = np.asarray([0.2, 0.8, -0.5])
bias = 2.0
# 输出应该是1x3(1行3列)x 3x1(3行1列)+ bias
print(inputs.shape, weights.shape)
# 应该先转化一下shape
inputs = inputs.reshape(1,3)
weights = weights.reshape(3,1)
# 再看一下
print(inputs.shape, weights.shape)
outputs = inputs @ weights + bias
print(outputs)
当然现在shape是1x1,变成了二维数组,我们只需要取标量


细节就是:
python
# this will be the input to our current neuron
inputs = np.array([1, 2, 3])
# every unique input will have a unique weight associated with it
# since we have three inputs, we have 3 weights
weights = np.array([0.2, 0.8, -0.5])
# every unique neuron has a unique bias
bias = 2
# output from our neuron is the input*weight + bias
output = inputs[0]*weights[0] + inputs[1]*weights[1] + inputs[2]*weights[2] + bias
print(output)其他的一些深度学习矩阵运算符的对照表:
| 运算名称 | 运算符 / 函数 | 作用 | 深度学习应用场景 | 示例(基于本文数据) |
|---|---|---|---|---|
| 矩阵转置 | .T |
行列互换,改变维度顺序 | 维度适配、注意力机制中的矩阵变换 | weights_3x1.T → 形状 (1,3) |
| 广播加法 | + |
标量 / 向量与矩阵自动扩展相加 | 偏置项添加(核心操作) | (inputs_1x3 @ weights_3x1) + bias |
| 元素级激活 | np.maximum() |
ReLU 激活函数实现 | 隐藏层激活,引入非线性 | np.maximum(matmul_result, 0) → [[0.3]] |
| 批量矩阵乘法 | np.matmul() |
多组矩阵同时相乘 | 批量处理样本((batch, in_dim) × (in_dim, out_dim) ) |
若 inputs_batch 形状 (2,3) ,可直接乘 weights_3x1 |
返回到我们前面的计算:
现在让我们来模拟输出层的一个神经元(第 4 层,最顶层的神经元)

这个和前面的有区别吗?

其实没有,先自己手动写一下简单的矩阵运算:
plain
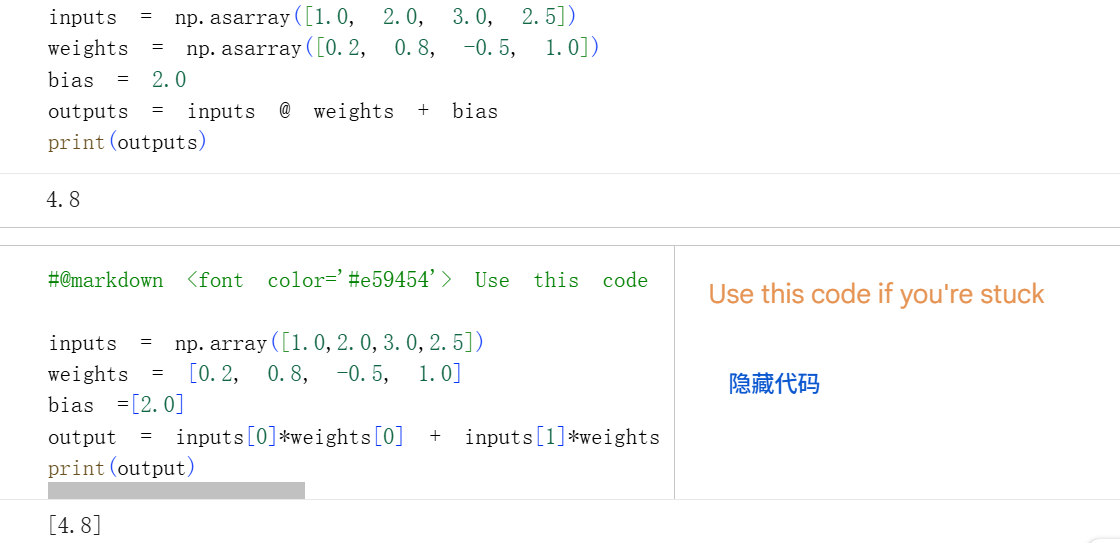
inputs = np.asarray([1.0, 2.0, 3.0, 2.5])
weights = np.asarray([0.2, 0.8, -0.5, 1.0])
bias = 2.0
outputs = inputs @ weights + bias
print(outputs)这里我们并没有reshape,而是直接按照一维数组的乘法

这是因为 NumPy 对一维数组的 @ 运算符做了特殊处理,它会自动将一维数组的矩阵乘法等价为点积运算,无需手动 reshape 成二维矩阵。
2,Coding a layer of neurons 编写神经元层

使用列表的列表(多维数组构建)来计算输出
如何构建一个包含 3 个神经元、每个神经元有 3 个输入的模型?
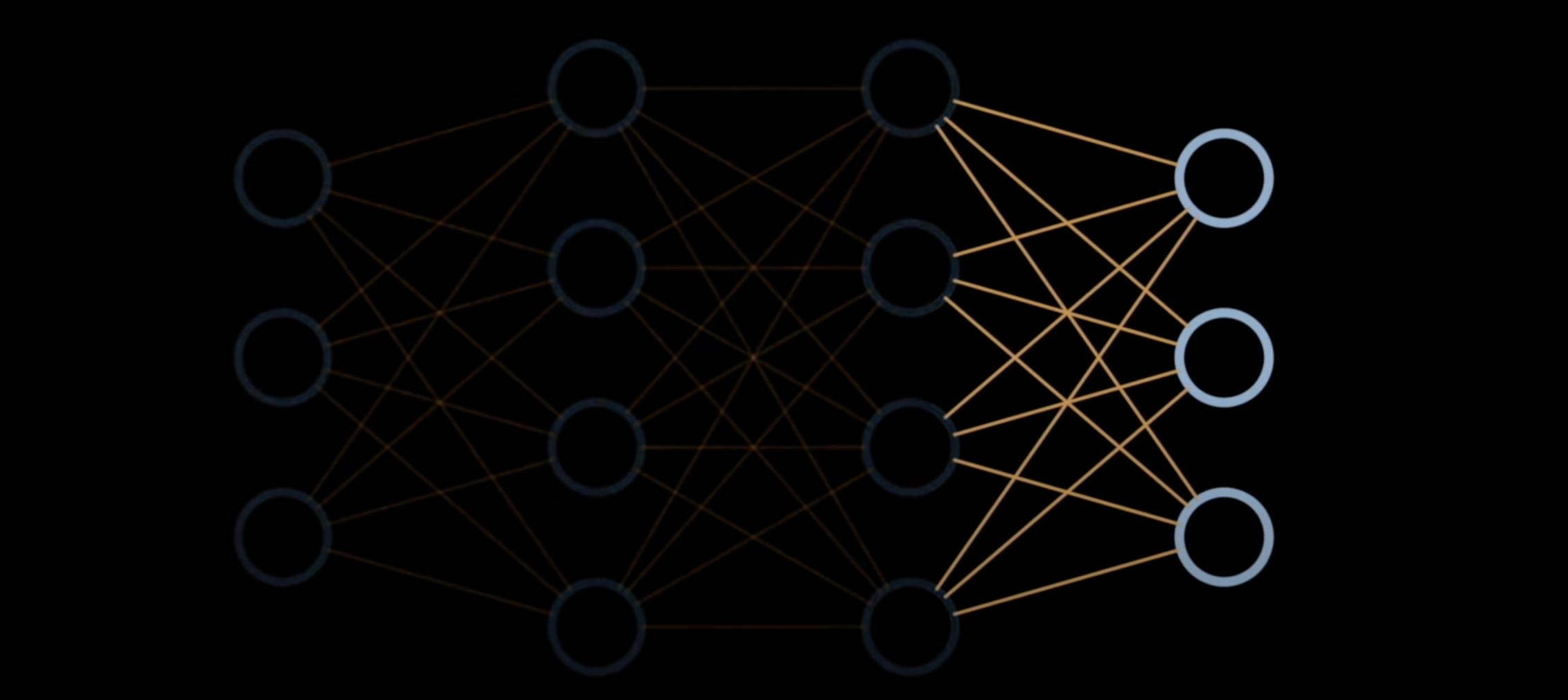
就拿上面这一个输出层为例来看,因为输出有3个神经元,倒数第2层是输入有4个神经元,
所以情况就是:
有4个输入,对应输出的3个神经元也就需要3个独特的权重集,每一个权重集有4个值(对应4个输入),另外每一个输出的神经元需要1个独特的bias
------》也就是4个输入,3个权重,3个bias(权重和bias维度与输出对齐)
python
# inputs are from hidden layer
inputs = np.array([1, 2, 3, 2.5])
# neuron 1 (top)
weights1 = np.array([0.2, 0.8, -0.5, 1.0])
bias1 = 2
# neuron 2 (middle)
weights2 = np.array([0.5, -0.91, 0.26, -0.5])
bias2 = 3
# neuron 3 (bottom)
weights3 = np.array([-0.26, -0.27, 0.17, 0.87])
bias3 = 0.5
# 3 neurons, with 4 inputs each
# each neuron has unique set of weights and a separate bias
# since our layer has 3 neurons, the layer output should be 3 values (one value for each of the neurons)
output = [inputs[0]*weights1[0] + inputs[1]*weights1[1] + inputs[2]*weights1[2] + inputs[3]*weights1[3]+ bias1,
inputs[0]*weights2[0] + inputs[1]*weights2[1] + inputs[2]*weights2[2] + inputs[3]*weights2[3]+ bias2,
inputs[0]*weights3[0] + inputs[1]*weights3[1] + inputs[2]*weights3[2] + inputs[3]*weights3[3]+ bias3]
print(output)简单来说就是输入是1x4,1行4列,输出是1x3,1行3列,
所以中间系数矩阵是4x3,bias是系数x输入之后的1x3,1行3列。
按照我们正常的习惯:
python
# inputs are from hidden layer
inputs = np.array([1, 2, 3, 2.5])
# neuron 1 (top)
weights1 = np.array([0.2, 0.8, -0.5, 1.0])
bias1 = 2
# neuron 2 (middle)
weights2 = np.array([0.5, -0.91, 0.26, -0.5])
bias2 = 3
# neuron 3 (bottom)
weights3 = np.array([-0.26, -0.27, 0.17, 0.87])
bias3 = 0.5
# 注意输入是4行1列
inputs = inputs.reshape(4,1)
# 权重是4行3列
weights = np.asarray([[weights1], [weights2], [weights3]])
print(weights.shape)
weights = weights.reshape(3,4).T
print(weights, weights.shape)
完整的就是:
python
# inputs are from hidden layer
inputs = np.array([1, 2, 3, 2.5])
# neuron 1 (top)
weights1 = np.array([0.2, 0.8, -0.5, 1.0])
bias1 = 2
# neuron 2 (middle)
weights2 = np.array([0.5, -0.91, 0.26, -0.5])
bias2 = 3
# neuron 3 (bottom)
weights3 = np.array([-0.26, -0.27, 0.17, 0.87])
bias3 = 0.5
# 注意输入是1行4列
inputs = inputs.reshape(1,4)
# 权重是4行3列
weights = np.asarray([[weights1], [weights2], [weights3]])
print(weights.shape)
weights = weights.reshape(3,4).T
print(weights, weights.shape)
# 偏置bias是1行3列
bias = np.asarray([bias1, bias2, bias3])
print(bias,bias.shape)
# 再reshape一下
bias = bias.reshape(1,3)
outputs = inputs @ weights + bias
print(outputs.shape, outputs)

python
inputs = np.array([1, 2, 3, 2.5])
# lets format the weights as a list of lists
weights = np.array([[0.2, 0.8, -0.5, 1.0],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]])
print("weights = ", weights)
# and a list for the biases
biases = np.array([2,
3,
0.5])
print("bias =", bias)
# output of current layer
layer_outputs = []
# zip together weights and biases (combines 2 lists into list of lists element-wise)
for neuron_weights, neuron_bias in zip(weights, biases):
# output of given neuron
neuron_output = 0
for n_input, weight in zip(inputs, neuron_weights):
# sum the inputs * weights
# 注意inputs只有1个值np.array([1, 2, 3, 2.5]),weight其实是3行4列
# 这里逐元素乘法实际上就是将仅有的1个inputs和3行中的任意一个weights进行逐元素乘法,获取1个标量
neuron_output += n_input*weight
# add the bias term
neuron_output += neuron_bias
# output from neurons
layer_outputs.append(neuron_output)
print("output =", layer_outputs)
总的来说,对于有些许数学直觉的人来说,数组之间的维度其实会更加敏感。
所以我们最好是写一个可以直接可视化数组张量维度的函数:
一个简单的可视化函数
python
import numpy as np
def visualize_numpy_array(arr):
"""
可视化NumPy数组的形状和结构
"""
print("=" * 50)
print(f"数组内容:\n{arr}")
print("-" * 50)
# 打印核心形状信息
shape = arr.shape
dim = arr.ndim
size = arr.size
print(f"数组形状 shape = {shape} → {dim}维数组")
print(f"数组元素总数 size = {size}")
print(f"维度含义:{' × '.join([f'第{i+1}维={s}' for i, s in enumerate(shape)])}")
print("=" * 50)
# 示例
weights = np.array([[0.2, 0.8, -0.5, 1.0],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]])
visualize_numpy_array(weights)
我们可以写得再详细一点:
python
def visualize_numpy_array(arr):
"""
可视化NumPy数组的形状和结构(层次化输出格式)
"""
# 确保输入是numpy数组
if not isinstance(arr, np.ndarray):
arr = np.asarray(arr)
# 定义分隔线样式,区分不同层级
LINE_TOP = "=" * 60
LINE_MID = "-" * 60
LINE_SUB = "~" * 60
print(LINE_TOP)
print(f"【1. 数组基础信息】")
print(LINE_SUB)
# 打印数组内容,根据维度调整显示缩进
if arr.ndim <= 2:
print(f"数组内容:\n{arr}")
else:
print(f"高维数组内容(前3个维度切片):\n{arr[:2] if arr.shape[0]>2 else arr}")
print(LINE_MID)
# 核心形状信息(层次化排版)
shape = arr.shape
dim = arr.ndim
size = arr.size
dtype = arr.dtype
print(f"【2. 核心维度参数】")
print(LINE_SUB)
print(f" ✅ 数组维度数 → {dim} 维")
print(f" ✅ 数组形状 → shape = {shape}")
print(f" ✅ 维度含义 → {' × '.join([f'第{i+1}维={s}' for i, s in enumerate(shape)])}")
print(f" ✅ 总元素数量 → size = {size}")
print(f" ✅ 数据类型 → dtype = {dtype}")
print(LINE_TOP)
python
inputs = np.array([1, 2, 3, 2.5])
# lets format the weights as a list of lists
weights = np.array([[0.2, 0.8, -0.5, 1.0],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]])
print("weights = ", weights)
visualize_numpy_array(weights)
# and a list for the biases
biases = np.array([2,
3,
0.5])
print("bias =", biases)
visualize_numpy_array(biases)
# output of current layer
layer_outputs = []
print("\n\n\n\n\n\n\n\n\n","*"*50,"\n","In Loop Now")
# zip together weights and biases (combines 2 lists into list of lists element-wise)
for neuron_weights, neuron_bias in zip(weights, biases):
# output of given neuron
neuron_output = 0
print(f"neuron_weights here is {neuron_weights}")
visualize_numpy_array(neuron_weights)
for n_input, weight in zip(inputs, neuron_weights):
# sum the inputs * weights
# 注意inputs只有1个值np.array([1, 2, 3, 2.5]),weight其实是3行4列
# 这里逐元素乘法实际上就是将仅有的1个inputs和3行中的任意一个weights进行逐元素乘法,获取1个标量
print(f"n_input here is {n_input}")
visualize_numpy_array(n_input)
print(f"weight here is {weight}")
visualize_numpy_array(weight)
neuron_output += n_input*weight
print(f"neuron_output now is {neuron_output}")
visualize_numpy_array(neuron_output)
# add the bias term
print(f"neuron_bias now is {neuron_bias}")
visualize_numpy_array(neuron_bias)
neuron_output += neuron_bias
print(f"neuron_output now is {neuron_output}")
visualize_numpy_array(neuron_output)
# output from neurons
layer_outputs.append(neuron_output)
print(f"layer_outputs now is {layer_outputs}")
visualize_numpy_array(layer_outputs)
print("output =", layer_outputs)
python
weights = [[ 0.2 0.8 -0.5 1. ]
[ 0.5 -0.91 0.26 -0.5 ]
[-0.26 -0.27 0.17 0.87]]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[[ 0.2 0.8 -0.5 1. ]
[ 0.5 -0.91 0.26 -0.5 ]
[-0.26 -0.27 0.17 0.87]]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 2 维
✅ 数组形状 → shape = (3, 4)
✅ 维度含义 → 第1维=3 × 第2维=4
✅ 总元素数量 → size = 12
✅ 数据类型 → dtype = float64
============================================================
bias = [2. 3. 0.5]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[2. 3. 0.5]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (3,)
✅ 维度含义 → 第1维=3
✅ 总元素数量 → size = 3
✅ 数据类型 → dtype = float64
============================================================
**************************************************
In Loop Now
neuron_weights here is [ 0.2 0.8 -0.5 1. ]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[ 0.2 0.8 -0.5 1. ]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (4,)
✅ 维度含义 → 第1维=4
✅ 总元素数量 → size = 4
✅ 数据类型 → dtype = float64
============================================================
n_input here is 1.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.2
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.2
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 0.2
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.2
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.8
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.8
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 1.8
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.8
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 3.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
3.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is -0.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 0.30000000000000004
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.30000000000000004
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 1.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 2.8
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.8
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_bias now is 2.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 4.8
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
4.8
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
layer_outputs now is [np.float64(4.8)]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[4.8]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (1,)
✅ 维度含义 → 第1维=1
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_weights here is [ 0.5 -0.91 0.26 -0.5 ]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[ 0.5 -0.91 0.26 -0.5 ]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (4,)
✅ 维度含义 → 第1维=4
✅ 总元素数量 → size = 4
✅ 数据类型 → dtype = float64
============================================================
n_input here is 1.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 0.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is -0.91
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.91
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -1.32
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-1.32
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 3.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
3.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.26
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.26
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -0.54
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.54
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is -0.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -1.79
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-1.79
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_bias now is 3.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
3.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 1.21
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.21
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
layer_outputs now is [np.float64(4.8), np.float64(1.21)]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[4.8 1.21]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (2,)
✅ 维度含义 → 第1维=2
✅ 总元素数量 → size = 2
✅ 数据类型 → dtype = float64
============================================================
neuron_weights here is [-0.26 -0.27 0.17 0.87]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[-0.26 -0.27 0.17 0.87]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (4,)
✅ 维度含义 → 第1维=4
✅ 总元素数量 → size = 4
✅ 数据类型 → dtype = float64
============================================================
n_input here is 1.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is -0.26
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.26
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -0.26
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.26
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is -0.27
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.27
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -0.8
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.8
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 3.0
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
3.0
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.17
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.17
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is -0.29000000000000004
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
-0.29000000000000004
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
n_input here is 2.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
weight here is 0.87
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.87
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 1.8849999999999998
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
1.8849999999999998
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_bias now is 0.5
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
0.5
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
neuron_output now is 2.385
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
2.385
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 0 维
✅ 数组形状 → shape = ()
✅ 维度含义 →
✅ 总元素数量 → size = 1
✅ 数据类型 → dtype = float64
============================================================
layer_outputs now is [np.float64(4.8), np.float64(1.21), np.float64(2.385)]
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[4.8 1.21 2.385]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (3,)
✅ 维度含义 → 第1维=3
✅ 总元素数量 → size = 3
✅ 数据类型 → dtype = float64
============================================================
output = [np.float64(4.8), np.float64(1.21), np.float64(2.385)]

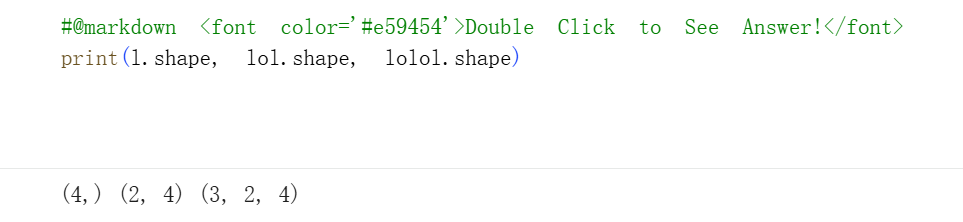
我们将处理形状和大小各异的数组。以下是其中的三个:
python
# type: list, 1D array, vector
l = np.array([1, 5, 6, 2])
# type: list of lists, 2D array, matrix
lol = np.array([[1, 5, 6, 2],
[3, 2, 1, 3]])
# type: list of list of lists, 3D array
lolol = np.array([[[1, 5, 6, 2],
[3, 2, 1, 3]],
[[5, 2, 1, 2],
[6, 4, 8, 4]],
[[2, 8, 5, 3],
[1, 1, 9, 4]]])我们可以使用 .shape numpy 方法打印上面每个tensor的形状
python
for i in [l,lol,lolol]:
visualize_numpy_array(i)
print("\n\n\n")
python
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[1 5 6 2]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 1 维
✅ 数组形状 → shape = (4,)
✅ 维度含义 → 第1维=4
✅ 总元素数量 → size = 4
✅ 数据类型 → dtype = int64
============================================================
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
数组内容:
[[1 5 6 2]
[3 2 1 3]]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 2 维
✅ 数组形状 → shape = (2, 4)
✅ 维度含义 → 第1维=2 × 第2维=4
✅ 总元素数量 → size = 8
✅ 数据类型 → dtype = int64
============================================================
============================================================
【1. 数组基础信息】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
高维数组内容(前3个维度切片):
[[[1 5 6 2]
[3 2 1 3]]
[[5 2 1 2]
[6 4 8 4]]]
------------------------------------------------------------
【2. 核心维度参数】
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
✅ 数组维度数 → 3 维
✅ 数组形状 → shape = (3, 2, 4)
✅ 维度含义 → 第1维=3 × 第2维=2 × 第3维=4
✅ 总元素数量 → size = 24
✅ 数据类型 → dtype = int64
============================================================
请注意数组必须是同构的:在每个维度上,它们需要具有相同的大小!
点积的概念

对于一维数组而言,点积就是逐元素乘法,

python
# dot product in numpy for a layer of neurons
inputs = np.array([1, 2, 3, 2.5])
weights = np.array([[0.2, 0.8, -0.5, 1.0],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]])
biases = np.array([2, 3, 0.5])
output = np.dot(weights, inputs) + biases # now order DOES matter
# here we perform the dot product 3 times:
# [np.dot(weights[0], inputs),
# np.dot(weights[1], inputs),
# np.dot(weights[2], inputs)] = [2.8, -1.79, 1.885]
# then add biases:
# np.dot(weights, inputs) + biases = [2.8, -1.79, 1.885] + [2.0, 3.0, 0.5] = [4.8, 1.21, 2.385]
print(output)关于批次batch的解释

3,Hidden layer activation functions 隐藏层激活函数


在阶跃函数中,如果输入大于 0,输出为 1,否则输出为 0。
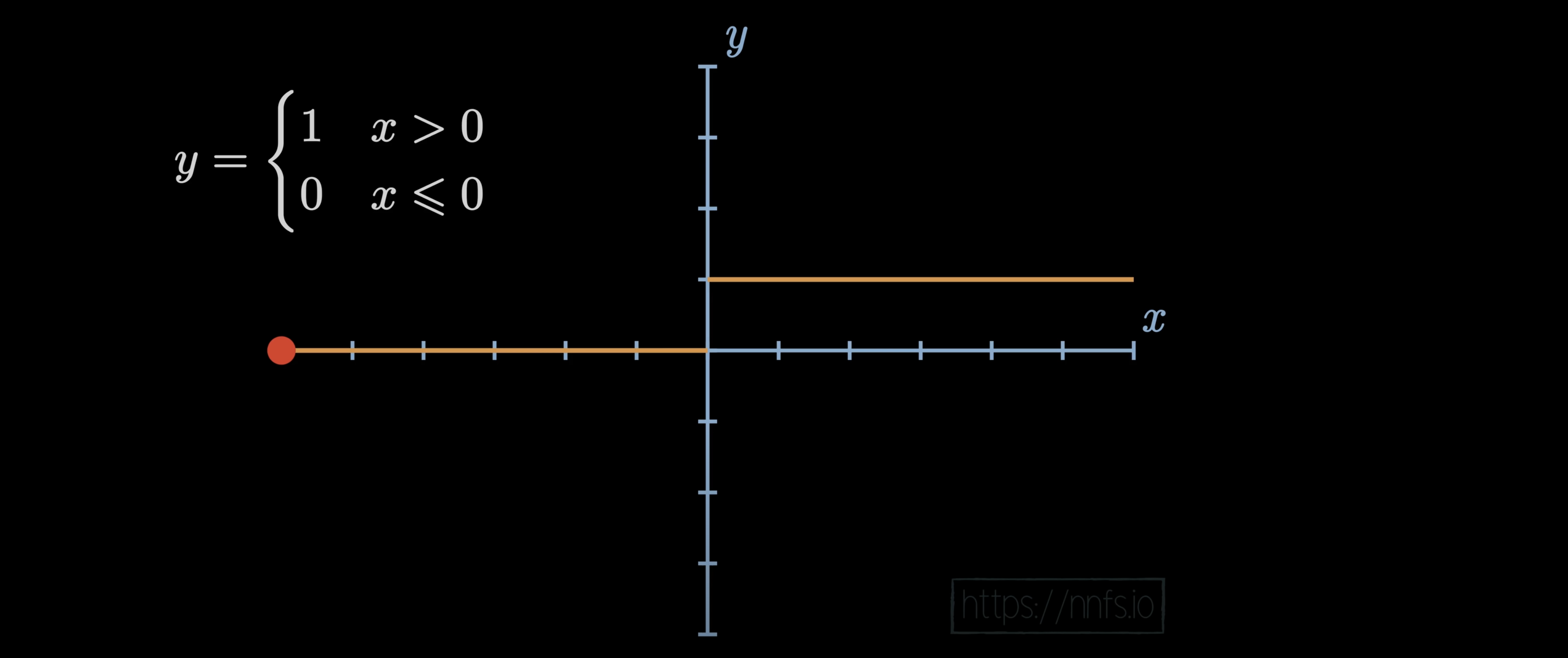
因此,在阶跃函数的情况下,您的神经元的输出字面值上是 0 或 1。
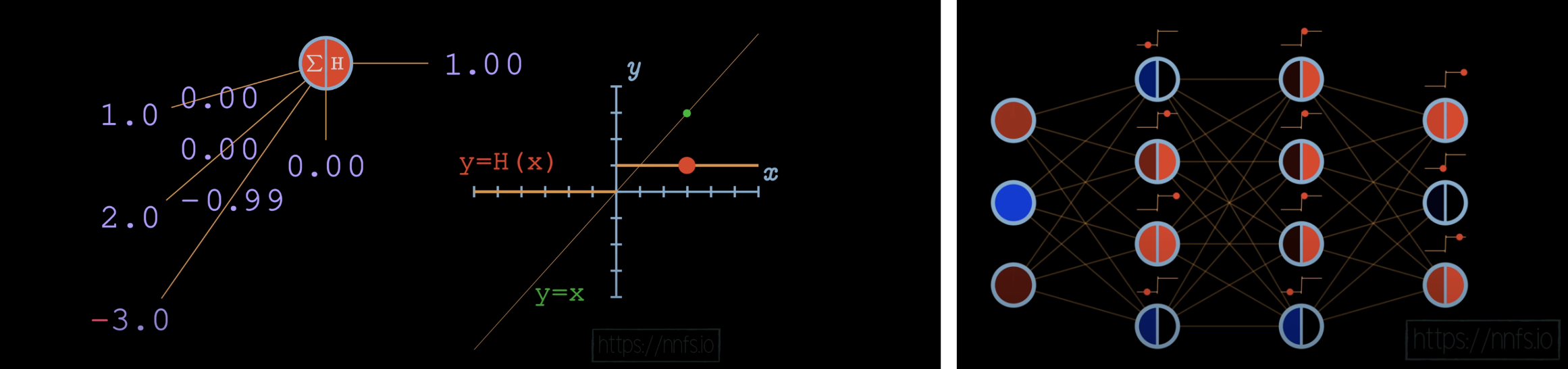

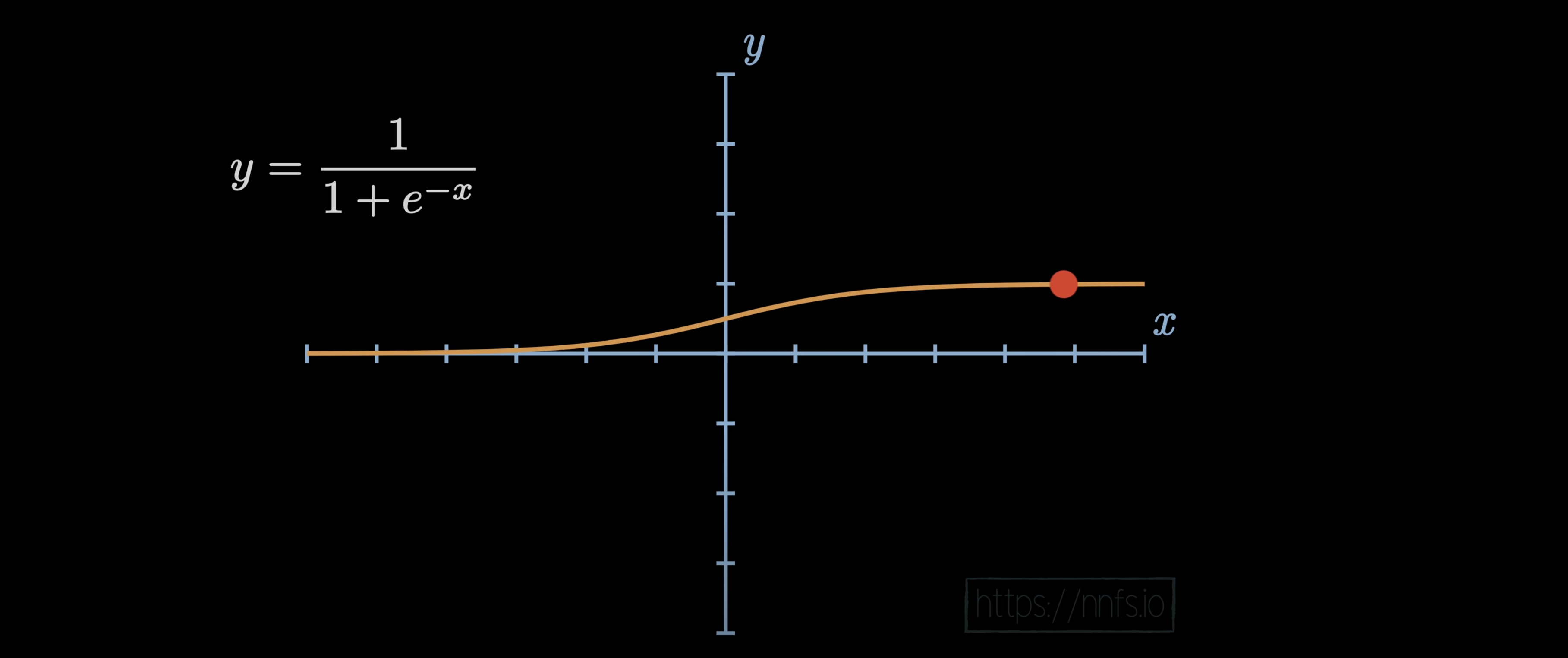

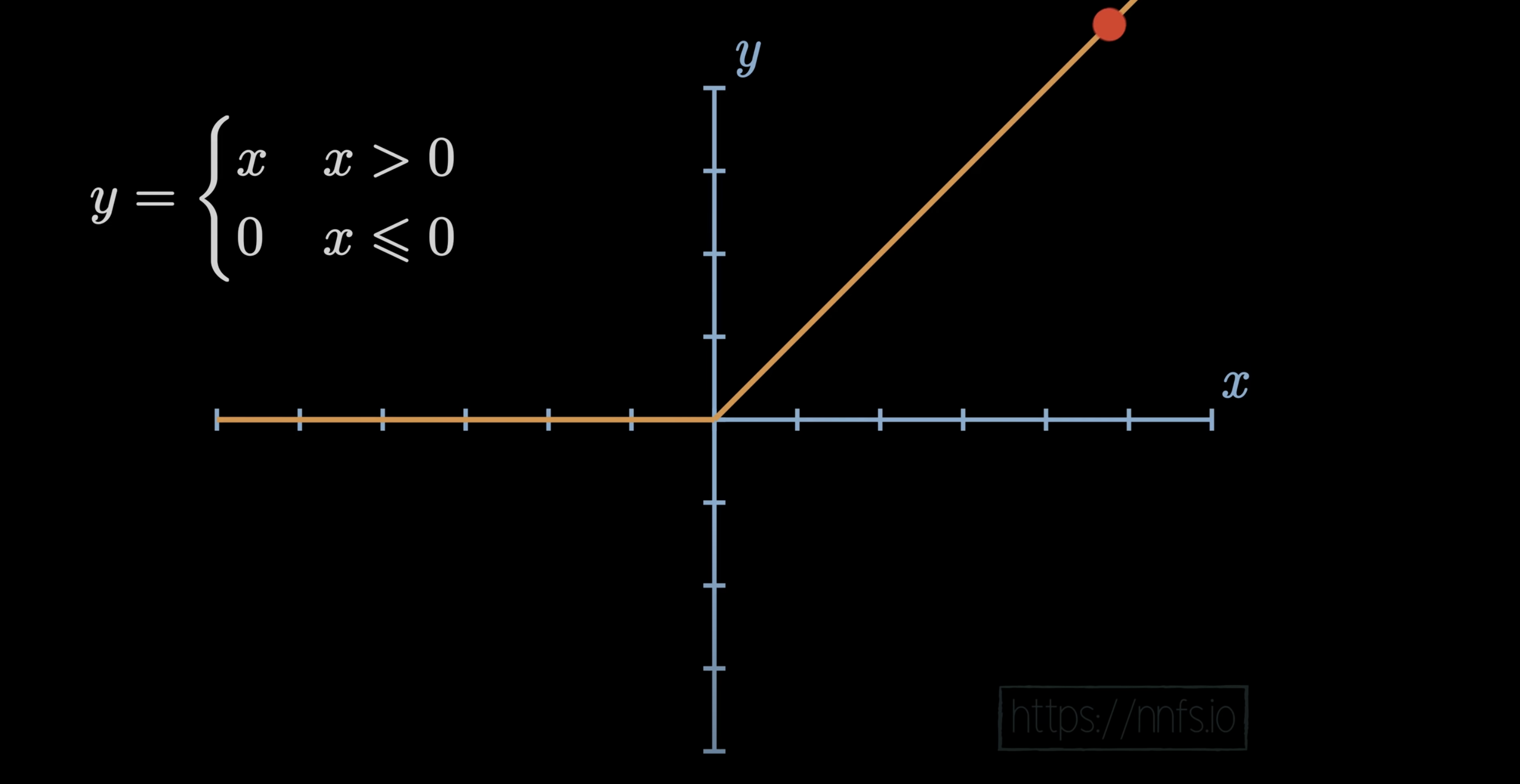

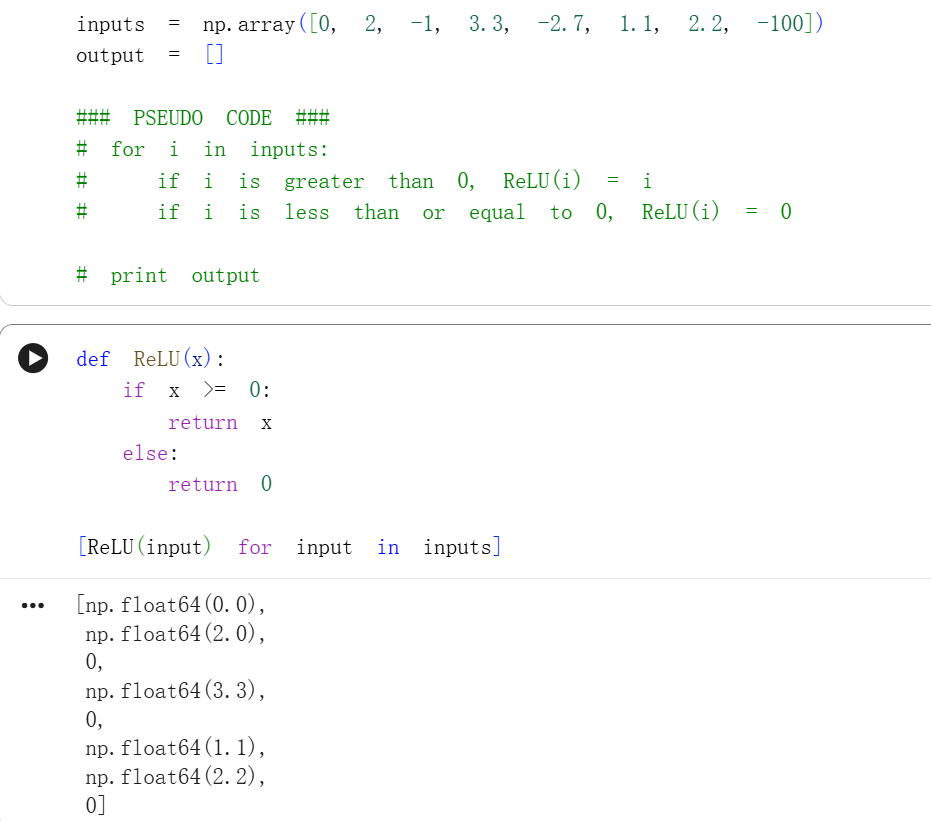


对应解释就是:


4,Output layer activation function 输出层激活函数

softmax



python
from math import exp
def softmax(x):
sum1 = sum([exp(i) for i in x])
return [exp(i)/sum1 for i in x]
softmax(layer_outputs1), softmax(layer_outputs2)或者直接使用numpy中的函数,接受numpy.ndarray作为输入:

python
#since we want to calculate the softmax for 2 outputs, instead of writing the code twice we can write a function instead
def calculate_softmax(layer_output):
softmax = np.exp(layer_output)/ np.sum(np.exp(layer_output))
return softmax
s1 = calculate_softmax(layer_outputs1)
sum1 = np.sum(s1)
s2 = calculate_softmax(layer_outputs2)
sum2 = np.sum(s2)
print(s1, sum1, s2, sum2)上面我们只是考虑一层输出,事实上我们会有一批batch输出:
python
# batch of 3 outputs
layer_outputs = np.array([[4.8, 1.21, 2.385], # output 1
[8.9, -1.81, 0.2], # output 2
[1.41, 1.051, 0.026]]) # output 3
#overflow prevention
layer_outputs = layer_outputs - layer_outputs.max()
exp_values = np.exp(layer_outputs)
# now, how do we do a sum? we use axis
# axis=1 is sum of rows, which is what we want
norm_values = exp_values / np.sum(exp_values, axis=1, keepdims=True)
print(norm_values)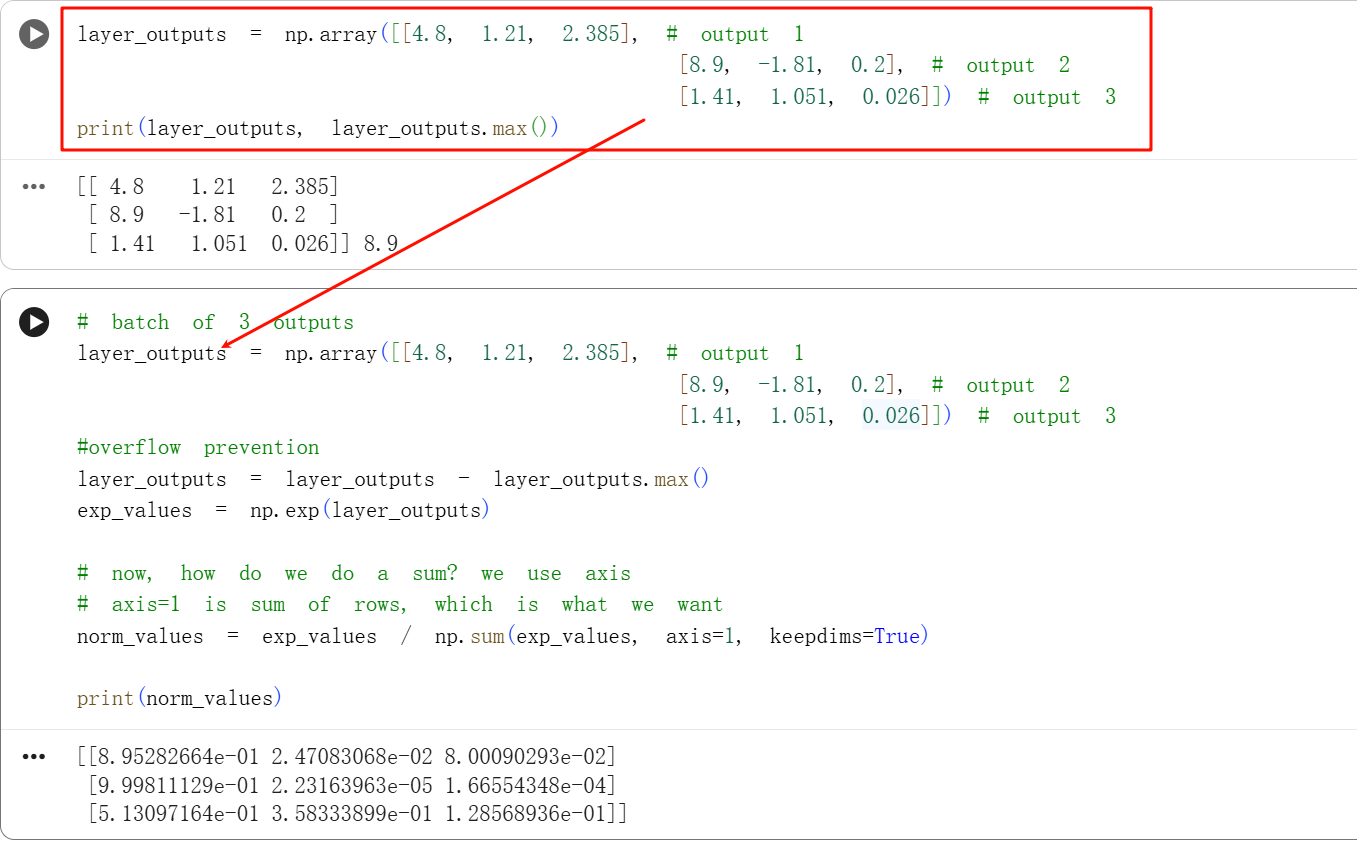
行0行,列1列,------》axis=0或者1,就按照行或者列的方向进行操作
比如说下面的求和,axis=1,也就是列1列,按照列的方向进行求和,(人是怎么数列的呢,就是横着数的,比如说第1列、第2列、第3列之类等),所以就是按照横的进行求和,也就是一行1个求和,所以行数也就是行的维度不会变,还是3行

overflow prevention 溢出预防

简单来说,就是指数运算容易爆表爆上限
5,Calculating and implementing loss 计算并实现损失



详细数学细节可以参考维基百科:
https://zh.wikipedia.org/wiki/交叉熵
http://en.wikipedia.org/wiki/Cross-entropy
pyTorch中的实现:
https://docs.pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html
比如说我们softmax输出某个样本的分布,比如说是某一个np.ndarray
python
softmax_output = np.array([0.7, 0.1, 0.2])
target_output = np.array([1, 0, 0]) # means target class is 1
target_class = 0
# 相当于前面讲的交叉熵损失函数, 样本只有1个, 也就是N=1,所以直接取第0个样本的预测概率即可
# 所以我们只需要直接看这个样本的所有类别的预测概率即可, 也就是只有K的数据
# cross-entropy loss for one sample and multiple classes
# cce = - Σ y_true * log( y_pred) # 因为N=1,所以省略了1/N
# cce = - Σ y_true * log( y_pred)
loss = -(math.log(softmax_output[0])*target_output[0] +
math.log(softmax_output[1])*target_output[1] +
math.log(softmax_output[2])*target_output[2])
print(loss)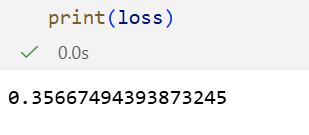
当然,其实眼尖的人能够立马看出我们的目标分类数据就是一个one-hot独热编码向量。

那么前面的计算逻辑其实能够进一步简化,独热编码下的交叉熵损失的简化逻辑就是:
- 当真实标签是独热编码时,交叉熵损失只与"真实类别对应的预测概率"有关,其余类别的预测概率因为乘0而不贡献。所以实际工程中,比如说是PyTorch/TensorFlow 的交叉熵损失函数,会直接用 "真实类别索引"(如 target_class=0)提取对应预测概率,避免不必要的求和计算,效率更高;
- 核心原因是 独热编码的 "0 项不贡献" 特性。
python
# since our true distribution has only one entry that equals 1 and the others are zero (one hot encoding), we can simply apply to the non-zero term
loss = -math.log(softmax_output[0])
print(loss)
如果猜的越不准,那么交叉熵就越大
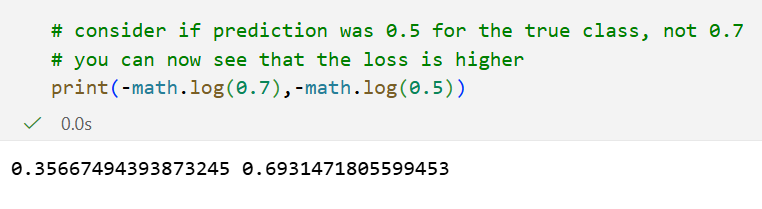
计算三张图像批次的损失
前面的例子是简单的单样本多类别分类,计算损失函数;现在我们来看一下多样本,每个样本多类别的损失函数。
比如说图像识别问题,
我们手头上有多个图片,比如说是3个样本,然后一共3个类别,
也就是我们的softmax激活函数输出是一个shape为3x3的输出矩阵。
python
softmax_outputs =np.array([[0.7, 0.1, 0.2], # prob distribution for image 1 (0.7)
[0.1, 0.5, 0.4], # ...image 2 (0.5)
[0.02, 0.9, 0.08]]) # ... image 3 (0.9)
# 0 = dog, 1 = cat, 2 = human
# image 1 dog, image 2 cat, image 3 cat
class_targets = [0, 1, 1]
print(softmax_outputs[[0, 1, 2], class_targets])
# softmax_outputs[[0,1,2]] 指的是取第0行、第1行、第2行
# 这一段等价于下面的代码
for i, j in enumerate(class_targets):
print(softmax_outputs[i][j])因为按照前面讲的,我们只需要真实label中类别(也就是真实类别)的预测概率,这对于计算交叉熵是有用的。
所以我们需要明确每一个样本对应其真实label中的类别的预测概率,
也就是取出softmax中第i个样本对应其真实label也就是第j列的值,
那么softmax_outputs[[0, 1, 2], class_targets],其实切片逻辑就是上面讲的zip一一取对应的。
python
# Apply loss function to our softmaxed values
# 其实就是每一个样本的交叉熵损失分别算
# 我们还是只要看当样本的逻辑
# 单样本前面演示了, 是 - Σ y_true * log( y_pred), 因为我们只看真实类别的独热贡献, 所以- 1 * log( y_pred ) = - log ( y_pred )
# 下面其实就是按照zip取对应值,然后算每一个y_pred的-log
neg_log = -np.log(softmax_outputs[
range(len(softmax_outputs)), class_targets
])
# 然后样本之间取均值
average_loss = np.mean(neg_log)
print(neg_log) # all cce's
print(average_loss) # average over batch
当然,很自然的,我们会遇到一个问题,就是如果在对应label处预测概率为0该怎么办------很常见,比如说预测器就是预测完全错误,会有log(0)。
一种选择是通过一个不显著的数量来裁剪值:
其实就是伪计数,给0值加上一个极小值来避免log0。
裁剪预测值可以确保我们不会遇到这个问题:
python
# y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)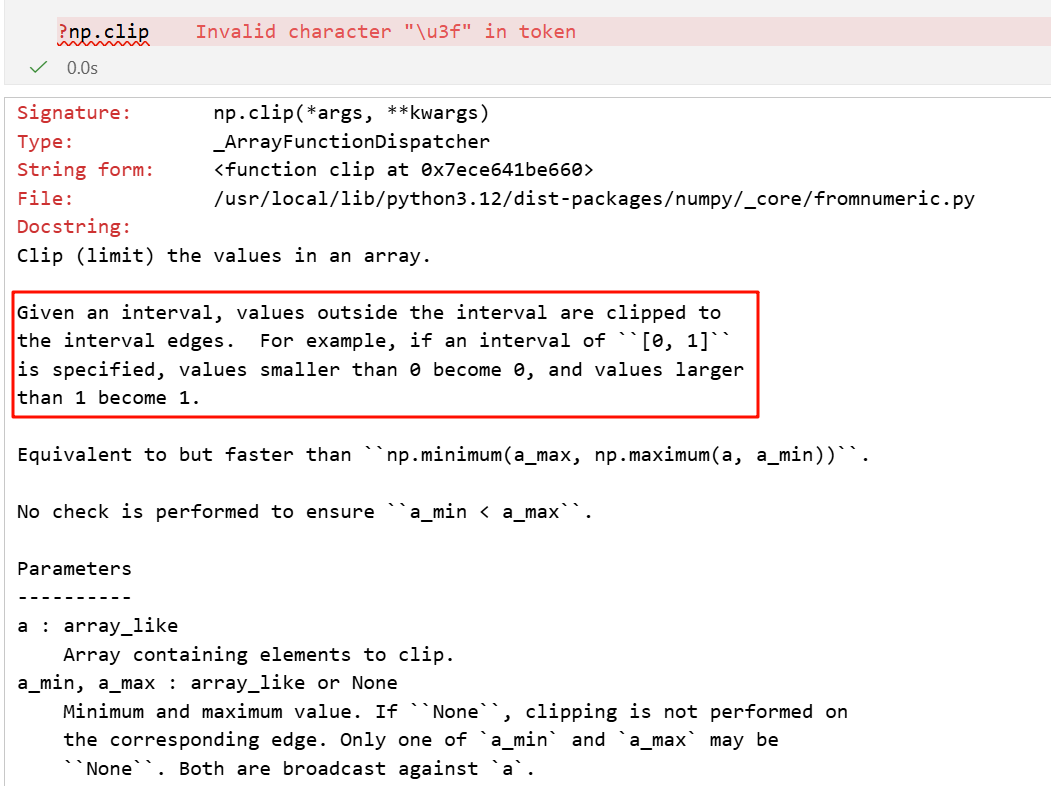
就是给定一个裁剪的上下界,然后数组中小于最小值的元素替换为下界,
数组中大于最大值的元素,替换为上界;
界于两者之间的元素保持不变。
那么我们如何解释准确率(Accuracy)?
其实准确率是针对于每个样本的类别预测问题/任务而定的,
所以其实我们光看softmax的输出,取预测概率最大的那个值/位置,看看位置/值和正确类别的是不是match,其实就是指示函数了。
那按照样本,也就是按照行来取每一行的列max(就是列1列的index,按照行取,也就是axis=1逻辑)。
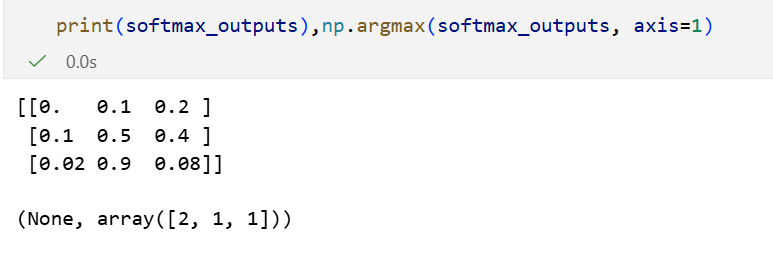
准确率,也就是位置匹配是2/3:
python
predictions = np.argmax(softmax_outputs, axis=1)
print(predictions)
print(class_targets)
# average of the amount of times prediction matches target class
accuracy = np.mean(predictions == class_targets)
print(accuracy)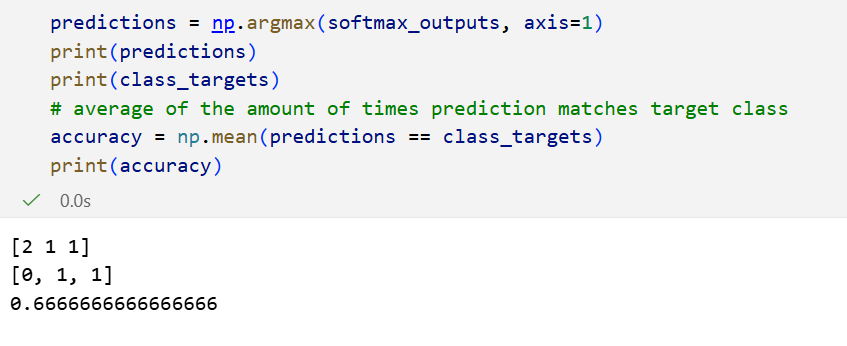
这里还有一个小细节容易搞混,就是矩阵/张量的索引/切片,其实这个也是numpy中的基础,就和前面提到的张量运算一样,但是就是基础不扎实的容易时刻犯迷糊。
step1:先明确「维度结构」
不管是几维张量,先把「维度顺序」和「每个维度的含义」拆清楚:
- 二维张量(矩阵):
(行维度, 列维度)→ 对应[行索引, 列索引] - 三维张量:
(样本维度, 通道维度, 高维度)→ 对应[样本索引, 通道索引, 高索引] - 通用规则:逗号分隔不同维度,每个维度内的索引 / 切片只作用于当前维度。
step2:按「索引类型」分类记忆
所有花式取数都可以归为 5 类,从简单到复杂逐一掌握:
| 索引类型 | 语法示例 | 作用说明 | 适用场景 |
|---|---|---|---|
| 单元素索引 | arr[2, 5] |
取第 2 行、第 5 列的单个元素(维度从 0 开始) | 精准取某个值 |
| 切片索引 | arr[1:4, :] |
取 1-3 行(左闭右开)、所有列 | 取连续的行 / 列 |
| 列表索引(花式) | arr[[0,2,4], [1,3,5]] |
取 (0,1)、(2,3)、(4,5) 三个元素 | 取离散的、成对的元素 |
| 列表索引(整行) | arr[[0,2,4], :] |
取 0、2、4 行的所有列 | 取离散的行 / 列 |
| 布尔索引 | arr[arr>0.5, :] |
取所有行中值 > 0.5 的行、所有列 | 按条件筛选元素 |
最容易搞混的其实就是列表索引 vs 切片索引
python
import numpy as np
arr = np.array([[1,2,3], [4,5,6], [7,8,9]])
# 切片:连续取行(1-2行),所有列 → 结果是二维数组
print(arr[1:3, :]) # [[4 5 6], [7 8 9]]
# 列表索引:离散取行(0、2行),所有列 → 结果也是二维数组
print(arr[[0,2], :]) # [[1 2 3], [7 8 9]]
# 列表索引(成对):取(0,1)、(2,2) → 结果是一维数组
print(arr[[0,2], [1,2]]) # [2, 9]
比如说最后一个,最容易搞混,我们很容易认为是取第0、2行,然后再取第1、2列,那么结果不应该是2x2 shape的tensor吗?
其实不是的,

其实我们可以发现,没有对切片套list的表达方式,
所以我们其实可以光看索引,[0,1]是list形式,0:2是切片形式。
python
# 列表索引(成对):[0,1]是列表,[1,2]也是列表------》列表索引
print(arr[[0,1], [1,2]])
print()
# 切片索引(指定行列的元素):0:2是切片,1:3也是切片------》切片索引
print(arr[0:2, 1:3]) # [[2 3], [5 6]]
# ✅ 关键:列表索引如果是「多维度成对」(如[行列表, 列表表]),是按位置一一对应取元素;如果是「单维度列表 + 其他维度切片」,是取「指定行 / 列的所有元素」。
✅ 关键:列表索引如果是「多维度成对」(如[行列表, 列表表]),是按位置一一对应取元素;如果是「单维度列表 + 其他维度切片」,是取「指定行 / 列的所有元素」。
列表索引在多维度同时使用时,不是「取行 + 取列」的笛卡尔积,而是「按位置配对取元素」。
明确两个完全不同的索引逻辑
| 需求描述 | 索引写法(正确) | 逻辑本质 | 结果形状 |
|---|---|---|---|
| 取 0、2 行 + 1、2 列(4 个元素) | arr[[0,2], :][:, [1,2]] 或 arr[np.ix_([0,2], [1,2])] |
先取行、再取列(笛卡尔积) | (2,2) |
| 取 (0,1)、(2,2) 两个元素 | arr[[0,2], [1,2]] |
按位置配对取元素(zip 逻辑) | (2,) |

Numpy/PyTorch 设计「多维度列表索引」时,核心规则是:
当多个维度同时传入等长的列表时,索引会按「位置一一配对」,而非「遍历所有组合」****。
所以,arr[[0,2], [1,2]] 其实等价于:
python
indices = list(zip([0,2], [1,2])) # 配对成[(0,1), (2,2)]
result = [arr[i,j] for i,j in indices] # 取arr[0,1]和arr[2,2]索引规则要求:第 k 个行索引 配 第 k 个列索引,最终只取「配对后的元素」,而非所有行 × 列的组合。
就是很符合zip的感觉。
这个规则不是 "反直觉",而是为了满足「按样本取对应类别」 这类高频场景:
- 比如 softmax 输出
(N,C),每个样本(行)要取对应的目标类别(列); - 如果用笛卡尔积,会取出
N×C个元素,完全不符合需求; - 而 zip 逻辑能精准实现「第 i 个样本取第 i 个类别」,这是深度学习、数据分析中最常用的花式索引场景。
什么时候是 zip,什么时候是笛卡尔积?
| 索引特征 | 执行逻辑 | 示例 | 结果 |
|---|---|---|---|
| 多维度都传等长列表 | zip 配对 | arr[[0,2], [1,2]] |
[2,9] |
只有一个维度传列表,其他用: |
笛卡尔积 | arr[[0,2], :] |
[[1,2,3],[7,8,9]] |
用np.ix_(行列表, 列表表) |
笛卡尔积 | arr[np.ix_([0,2],[1,2])] |
[[2,3],[8,9]] |
总之简单记忆:
多维度列表索引 = 按位置配对,单维度列表 + 切片 = 笛卡尔积
(行列列表取zip)。

多维度等长可迭代索引 = 按位置配对,和 "是不是列表" 无关
6,Backpropogation 反向传播

参考维基百科:https://en.wikipedia.org/wiki/Backpropagation
我们为什么需要导数和偏导数?
换句话说,为什么在深度学习中,我们会频繁地用到数学分析中这一部分的知识?
简单来说,了解各种操作的导数,是为了高效地优化模型的权重和偏差,从而最小化损失函数,这是机器学习(尤其是深度学习)中梯度下降算法的核心基础。
最直接地,loss是我们要优化的目标,参数(weights、bias等)是我们能够修改的。
我们想当然地希望知道输入如何变化,输出会如何变化,知道了规律之后我们才能够通过调整输入去影响输出、调整输出。
把某个参数调大一点,损失会变大还是变小?变化的幅度是多少?这就是微分/导数的基本概念。
- 随机调整参数行不通模型的权重和偏差是决定预测结果的关键参数。如果靠 "随机搜索" 去试不同的参数组合,不仅效率极低,还几乎不可能找到最优解 ------ 尤其是当模型有上万甚至上亿个参数时,这种方法完全不具备可行性。
- 参数调整的依据是 "对损失的影响"我们的目标是让模型的预测值尽可能接近真实值,也就是让损失函数的值变得最小。而要调整权重和偏差,首先得知道:把某个参数调大一点,损失会变大还是变小?变化的幅度是多少?这个 "参数对损失的影响程度",在数学上的量化指标就是导数(梯度)。导数的正负号告诉我们参数该往哪个方向调(正号表示调大参数会让损失增加,所以要调小;负号则相反),导数的绝对值告诉我们调整的幅度该多大。
- 正向传播的操作导数,是链式求导的前提神经网络的预测过程是正向传播:输入数据经过神经元的加权求和、激活函数等一系列操作,最终输出预测值并计算损失。而损失函数是关于所有权重、偏差和输入的复合函数,要计算参数对损失的导数,需要用到链式法则。这就要求我们必须先算出正向传播中每一个操作(比如加权运算 y=wx+b、激活函数 σ(y) 等)的导数,再通过链式法则把这些导数串联起来,最终得到参数对损失的梯度。




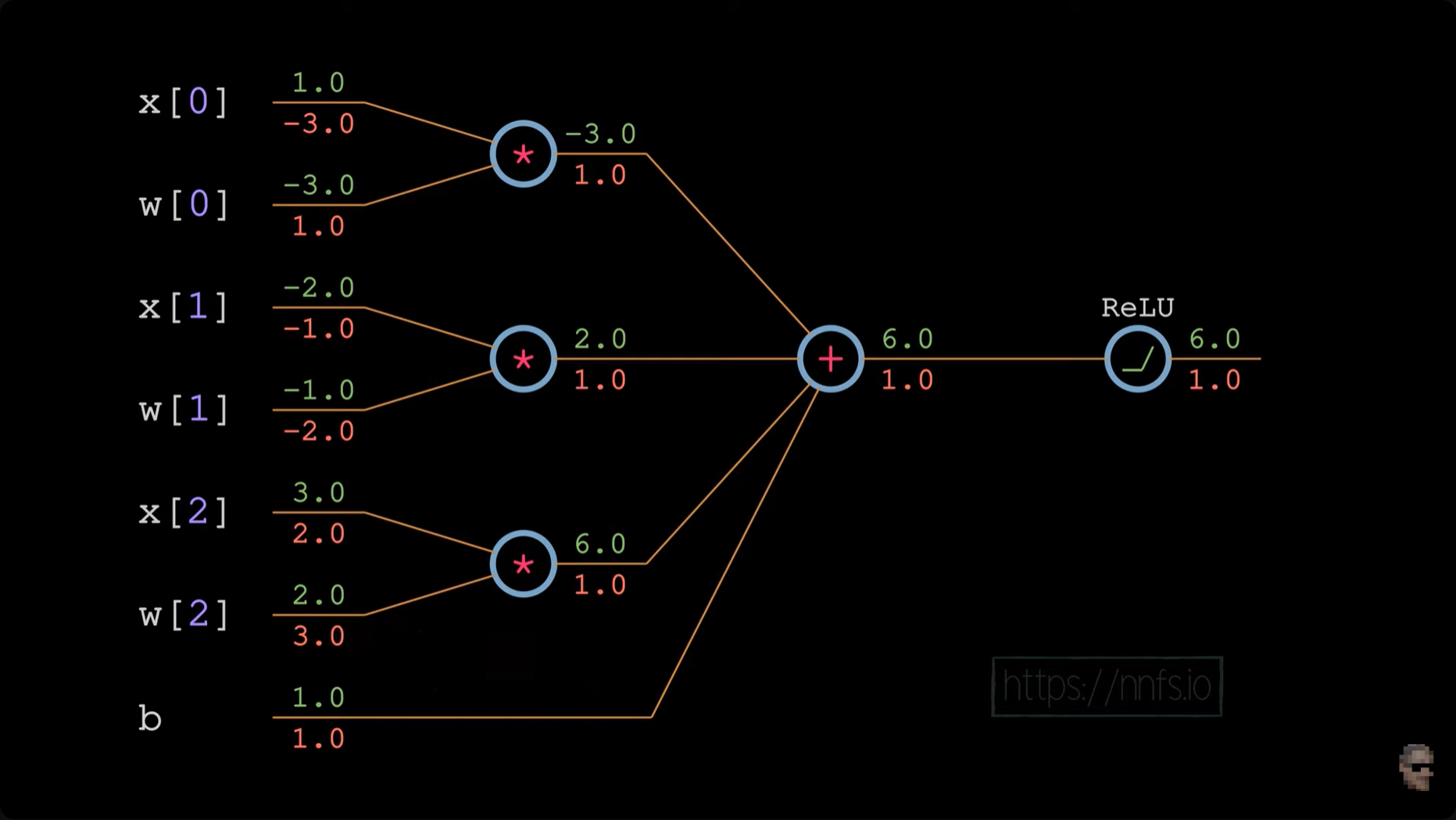
让我们反向传播单个神经元的 ReLU 函数,并假设我们打算最小化该单个神经元的输出。我们将利用链式法则和导数以及偏导数来计算每个变量对 ReLU 激活输出的影响。
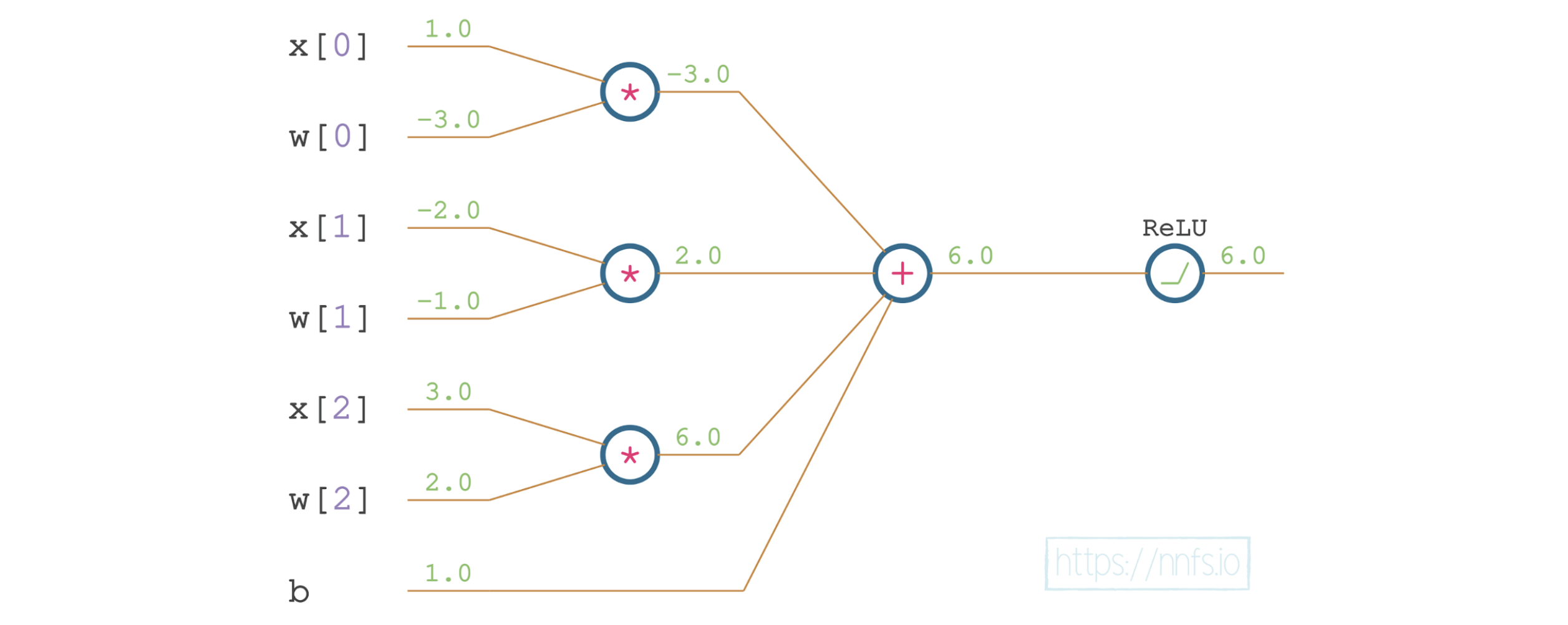
python
# neuron with 3 inputs
x = np.array([1.0, -2.0, 3.0]) # inputs
w = np.array([-3.0, -1.0, 2.0]) # weights
b = 1.0 # bias
## forward pass
# input*weights
xw0 = x[0] * w[0]
xw1 = x[1] * w[1]
xw2 = x[2] * w[2]
# add bias
z = xw0 + xw1 + xw2 + b
# ReLU activation function
y = max(z, 0)
print(y)
第一步是通过链式法则计算每个参数和输入的导数和偏导数,从而反向传播我们的梯度。我们面临的嵌套函数可以写成如下形式。
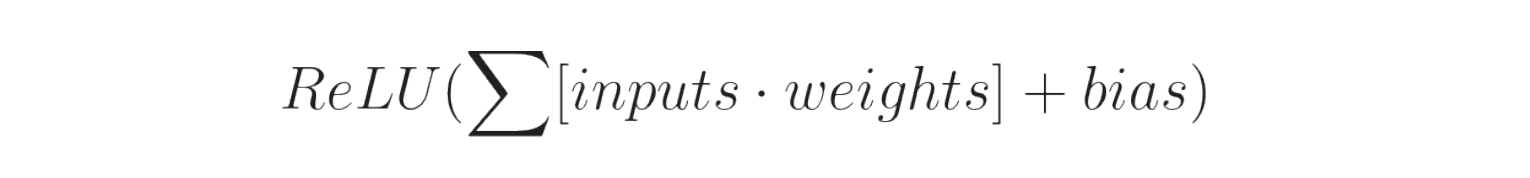
(在机器学习和数学语境中,wrt 是 with respect to 的缩写,意思是 "关于......")
1. 导数的两种核心用途:针对"参数" vs 针对"输入"
在反向传播中,会计算两类导数,它们的作用完全不同:
- 针对权重(weights)和偏置(bias)的导数
权重和偏置是神经网络的"可学习参数",其导数直接反映了"该参数的微小变化会如何影响最终的损失函数(Loss)"------导数绝对值越大,说明该参数对模型误差的影响越强。
这些导数最终会用于更新参数 (比如通过梯度下降:新参数 = 旧参数 - 学习率×导数),从而让模型逐步降低误差、提升性能。 - 针对层输入(layer inputs)的导数
层输入的导数不直接用于更新参数,而是为了串联多层网络。因为深层神经网络由"输入层→隐藏层→输出层"的链式结构组成,要计算前一层(更靠近输入层)参数的导数,必须先知道当前层输入的导数------通过将当前层输入的导数"传递给链中的前一个函数",才能反向推导前一层参数对损失的影响,实现"从输出层往输入层"的反向传播。
2. 反向传播的核心操作:损失函数导数 + 链式法则
要实现上述两种导数的计算,核心逻辑是两步:
- 计算损失函数的导数:损失函数(如交叉熵、MSE)衡量模型预测值与真实值的差距,其导数是反向传播的"起点"------告诉我们"当前模型误差的整体方向"。
- 应用链式法则:神经网络的每一层都由"线性变换(权重×输入+偏置)+ 激活函数(如ReLU、Sigmoid)"组成,多层叠加后相当于"函数的函数"。根据链式法则,需要将"损失函数的导数"与"所有连续层中激活函数的导数、神经元线性变换的导数"依次相乘,才能逐步推导到"权重/偏置的导数"和"前一层输入的导数"。
3. 反向传播的本质:"反向递推"的逻辑
为什么要"反向传播到前一层"?
因为模型的误差是在输出层产生的(预测值与真实值对比),但误差的根源可能来自前层参数的不合理(比如某隐藏层权重设置不当,导致后续层输入失真)。通过"层输入导数"的传递,能将输出层的误差"回溯"到前层,进而计算前层参数的导数并更新------这正是"反向传播"名字的由来,也是深层网络能有效学习的关键。
神经网络的计算是分层的正向流程:输入层 → 隐藏层 → 输出层,数据是从前往后 "流" 的,这叫正向传播。
而计算梯度的时候,必须反过来算:
梯度的起点是 输出层的损失函数(因为误差是在输出层才和真实标签对比出来的)。
然后从输出层往隐藏层、再往输入层倒着算 ------ 先算靠近输出层的参数梯度,再把梯度信息传递给前一层,算出前一层参数的梯度。
整个梯度的计算和传递方向,和数据正向流动的方向完全相反。
所以 "反向" 这个词,是精准描述了梯度的传递方向,不是随便起的。
从本质上讲,反向传播的概念本来就没有什么神奇的,就是我们正常理工科在大一学的数学分析中的链式法则的简单工程应用。
原理是万变不离其宗,应用场景可以很高大上,起个高大上的名字不影响我们看本质。
简单来说:反向传播是针对多层神经网络的 "定制版链式法则应用"------ 它明确了 "从损失出发、从后往前逐层算梯度" 的执行步骤,还规定了 "层与层之间梯度怎么传递"。
没有这个名字,工程师之间没法精准沟通 "怎么给神经网络算梯度",总不能每次都讲 "用链式法则从输出层倒着算权重梯度" 吧?

两个梯度:参数梯度与输入梯度
比如说算一个网络的的梯度信息的反向传播,
我们一定要明确,反向传播的梯度信息,是要计算两个梯度:
- 参数梯度:这个是毋庸置疑的,因为我们本身就是需要更新参数来调整loss,所以每一层对参数的求导也就是梯度是必要的
- 输入梯度:对输入层的求导,这个也是必要的,因为我们要更新的不是某一层的参数梯度,我们要更新的是所有层的参数梯度。举例来说,当前层的参数梯度更新完了,只能说当前层能够学习,如何把这个更新信息传递给上一层,让上一层也进行梯度更新?关键就是对当前层的输入进行求导,因为当前层的输入就是上一层的输出,这样我们就拿到了这一层与上一层的连接信息,那么这一层的输入梯度其实就相当于是上一层的输出梯度。我们可以把这个输出的梯度作为起点,那么我们此时的关注对象就自然迁移到了上一层,那么接着对参数求导,然后对上一层的输入求导(将梯度信息传递下去,这个是关键)

这段公式的写法逻辑,就是把每一个中间项都当成 "待传递的梯度节点",故意不把导数 "求尽",而是拆成一步步的链式传递。
而且也明写了既要求参数梯度(x0w0对w0求导),也要求输入梯度(x0w0对x0求导)。
公式里单独对x0w0求偏导,相当于把加权和
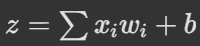 单独拆分成了求和--->乘积两个子步骤,反向传播时,梯度要先穿过"求和",再穿过"乘积",这两步都要单独算。
单独拆分成了求和--->乘积两个子步骤,反向传播时,梯度要先穿过"求和",再穿过"乘积",这两步都要单独算。

我以前刚入门的时候,对这里的步骤也很困惑,数学上能够理解,就是全微分与偏导数,很简单。
但是不明白为什么要每一步拆成这样写,
- 从数学上,全微分 / 链式法则是否要求必须同时对输入和参数求导?
- 为什么反向传播的公式里,非要把这两种导数都算出来,而不是只算参数导数?
答案很明确:从数学本质上,链式法则本身不强制要求同时算,但反向传播的工程目标(多层网络训练),决定了必须同时算这两类导数。

其实我们可以发现:

所以数学上,不是链式法则 "强制" 要算输入梯度,而是算参数梯度的中间产物,刚好可以 "顺便" 算出输入梯度------ 相当于买一送一,完全没必要浪费这个中间结果。
从工程目标上:多层网络训练,必须要输入梯度才能 "链式串联"。
这才是反向传播必须算输入梯度的根本原因,也是前面英文文档里反复强调的点:chain more layers
python
The derivative wrt the inputs are used to chain more layers by passing them to the previous function in the chain关键在于MLP多层网络,我们必须把梯度信息传给前一层,如果只算参数梯度那只能更新当前层,只有对输入也求梯度,才能将梯度传给前一层。

层与层之间的连接关系是本质需求



对当前层输入求导,本质是把当前层的梯度信号,转化为前一层的梯度起点,没有这个转化,梯度就无法 "回传" 到前一层,前一层也就没法计算自己的参数梯度。

回到我们前面的梯度反向传播的过程,代码细拆如下
python
## backward pass
# derivative from the next layer
dvalue = 1.0 # ∂y / ∂y = 1
print(dvalue)
# derivative of ReLU and chain rule
# (∂y / ∂y) * (∂ ReLU(z) / ∂
drelu_dz = dvalue * (1.0 if z > 0 else 0.)
print(drelu_dz)
# partial derivatives of summation, the chain rule
dsum_dxw0 = 1
dsum_dxw1 = 1
dsum_dxw2 = 1
dsum_db = 1
drelu_dxw0 = drelu_dz * dsum_dxw0
drelu_dxw1 = drelu_dz * dsum_dxw1
drelu_dxw2 = drelu_dz * dsum_dxw2
drelu_db = drelu_dz * dsum_db
print(drelu_dxw0, drelu_dxw1, drelu_dxw2, drelu_db)
# Partial derivatives of the multiplication and chain rule
dmul_dx0 = w[0]
dmul_dx1 = w[1]
dmul_dx2 = w[2]
dmul_dw0 = x[0]
dmul_dw1 = x[1]
dmul_dw2 = x[2]
drelu_dx0 = drelu_dxw0 * dmul_dx0
drelu_dw0 = drelu_dxw0 * dmul_dw0
drelu_dx1 = drelu_dxw1 * dmul_dx1
drelu_dw1 = drelu_dxw1 * dmul_dw1
drelu_dx2 = drelu_dxw2 * dmul_dx2
drelu_dw2 = drelu_dxw2 * dmul_dw2
print(drelu_dx0, drelu_dw0, drelu_dx1, drelu_dw1, drelu_dx2, drelu_dw2)

示例视频参考https://www.youtube.com/watch?v=_9qHQA30hys&t=2s
7,Optimizers 优化器


关于随机梯度下降,可以参考维基百科:
https://en.wikipedia.org/wiki/Stochastic_gradient_descent




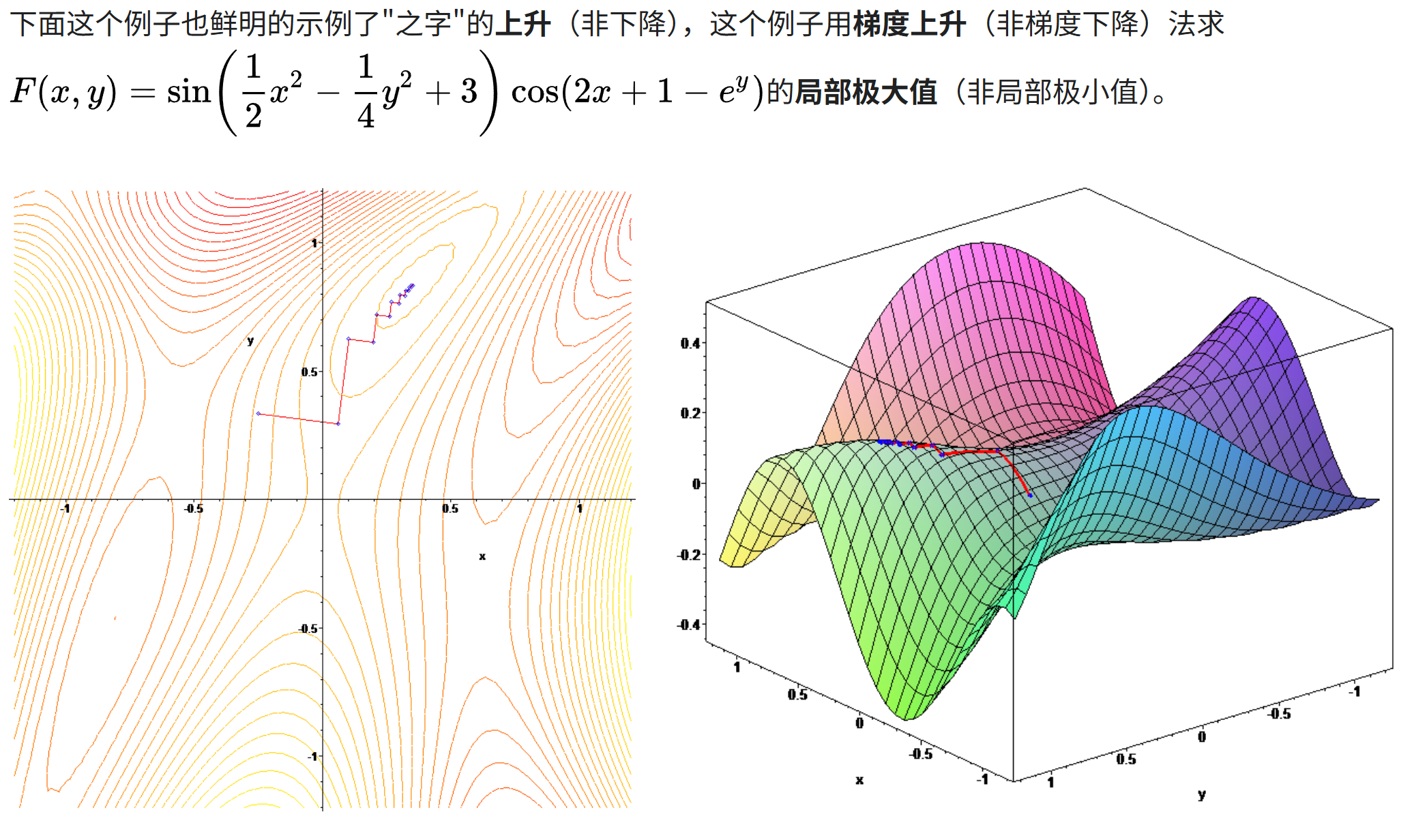


随机梯度下降(通常缩写为 SGD)是一种优化具有适当平滑性质的目标函数的迭代方法(例如可微或次可微)。它可以被视为梯度下降优化的随机近似,因为它用从随机选择的数据子集计算出的估计梯度来代替从整个数据集计算出的实际梯度。特别是在高维优化问题中,这减少了非常高的计算负担,以牺牲较低的收敛速度为代价,实现了更快的迭代。


一些数学严谨性的背后论证:

历史




SGD是一种基础的优化算法(概念很直观),动量和Adam等是在SGD的基础上进行改进和扩展的优化方法。SGD本身也是一种算法,而不是单纯的技巧,动量和Adam等方法通过引入特定的技巧来改进SGD的性能。
简单来说,SGD是基础优化算法(是算法),而动量、Adam等是技巧(trick),一般指通过技巧在SGD基础上进行改进和扩展的优化算法(简单理解就是SGD+技巧优化)。
更一般地说:SGD是一种基础优化算法,而动量和Adam等是在SGD的基础上引入了特定机制或策略来改进性能的优化算法。这些机制或策略可以被看作是"技巧",但它们本身构成了完整的优化算法。

8,Learning rate and momentum 学习率和动量



网上教材很多,总之要看通俗一点的解释,可以参考李宏毅老师油管的网课:
2021年网课版,这5节课1个系列,对于训练的一些常识解释得比较通俗易懂。





9,Complete Neural Network from scratch 从头开始构建完整的神经网络

定义模型:1个Workshop的示例
直接上代码
python
# Dense layer
class Layer_Dense:
"""
Dense layer of a neural network
Facilitates:
- Forward propogation of data throught layer
- Backward propogation of gradients during training
"""
# Layer initialization
def __init__(self, n_inputs, n_neurons):
# Initialize weights and biases
self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
self.biases = np.zeros((1, n_neurons))
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs, weights and biases
self.output = np.dot(inputs, self.weights) + self.biases
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
# ReLU activation
class Activation_ReLU:
"""
Rectified linear unit activation function
Applied to input of neural network layer
Introduces non-linearity into the network
"""
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs
self.output = np.maximum(0, inputs)
# Backward pass
def backward(self, dvalues):
# Since we need to modify original variable,
# let's make a copy of values first
self.dinputs = dvalues.copy()
# Zero gradient where input values were negative
self.dinputs[self.inputs <= 0] = 0
# Softmax classifier - combined Softmax activation
# and cross-entropy loss for faster backward step
class Activation_Softmax_Loss_CategoricalCrossentropy():
"""
Combination of softmax activation function and categorical cross entropy loss function
Commonly used in classification tasks
We minimize loss by adjustng model parameters to improve performance
"""
# create activation and loss function objectives
def __init__(self):
self.activation = Activation_Softmax()
self.loss = Loss_CategoricalCrossentropy()
# forward pass
def forward(self, inputs, y_true):
# output layer's activation function
self.activation.forward(inputs)
# set the output
self.output = self.activation.output
# calculate and return loss value
return self.loss.calculate(self.output, y_true)
# backward pass
def backward(self, dvalues, y_true):
# number of samples
samples = len(dvalues)
# if labels one-hot encoded, turn into discrete values
if len(y_true.shape) == 2:
y_true = np.argmax(y_true, axis=1)
# copy so we can safely modify
self.dinputs = dvalues.copy()
# Calculate gradient
self.dinputs[range(samples), y_true] -= 1
# Normalize gradient
self.dinputs = self.dinputs / samples
# Adam optimizer
class Optimizer_Adam:
"""
Adam optimization algorithm to optimize parameters of neural network
Initalize with learning rate, decay, epsilon, momentum
Pre-update params: Adjust learning rate based on decay
Update params: Update params using momentum and cache corrections
Post-update params: Track number of optimization steps performed
"""
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.beta_1 = beta_1
self.beta_2 = beta_2
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays, create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_momentums = np.zeros_like(layer.weights)
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# Update momentum with current gradients
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# Get corrected momentum
# self.iteration is 0 at first pass
# and we need to start with 1 here
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# update cache with squared current gradients
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# get corrected cache
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# Vanilla SGD parameter update + normalization with square root cache
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
# call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Softmax activation
class Activation_Softmax:
"""
Softmax activation function for multi-class classification
Compute probabilities for each class
"""
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Get unnormalized probabilities
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# Normalize them for each sample
probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
self.output = probabilities
# Backward pass
def backward(self, dvalues):
# Create uninitialized array
self.dinputs = np.empty_like(dvalues)
# Enumerate outputs and gradients
for index, (single_output, single_dvalues) in enumerate(zip(self.output, dvalues)):
# Flatten output array
single_output = single_output.reshape(-1, 1)
# Calculate Jacobian matrix of the output
jacobian_matrix = np.diagflat(single_output) - np.dot(single_output, single_output.T)
# Calculate sample-wise gradient and add it to the array of sample gradients
self.dinputs[index] = np.dot(jacobian_matrix, single_dvalues)
# Common loss class
class Loss:
# calculates data and regularization losses, given model output and ground truth values
def calculate(self, output, y):
# calculate sample losses
sample_losses = self.forward(output, y)
# calculate mean losses
data_loss = np.mean(sample_losses)
# return loss
return data_loss
# cross entropy loss
class Loss_CategoricalCrossentropy(Loss):
"""
Computes categorical cross entropy
Quantifies discrepency between predicted and true class probabilities
"""
# forward pass
def forward(self, y_pred, y_true):
# number samples in batch
samples = len(y_pred)
# clip data to prevent division by 0
# clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# probabilities for target values (only if categorical labels)
if len(y_true.shape) == 1:
correct_confidences = y_pred_clipped[ range(samples), y_true ]
# mask values (only for one-hot encoded labels)
elif len(y_true.shape) == 2:
correct_confidences = np.sum( y_pred_clipped * y_true, axis=1 )
# losses
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
# backward pass
def backward(self, dvalues, y_true):
# number of samples
samples = len(dvalues)
# Number of labels in every sample
# We'll use the first sample to count them
labels = len(dvalues[0])
if len(y_true.shape) == 1:
y_true = np.eye(labels)[y_true]
# calculate gradient
self.dinputs = -y_true / dvalues
# Normalize gradient
self.dinputs = self.dinputs / samples然后这一块因为我们要上gpu了,所以一些基础的东西也再提一下:
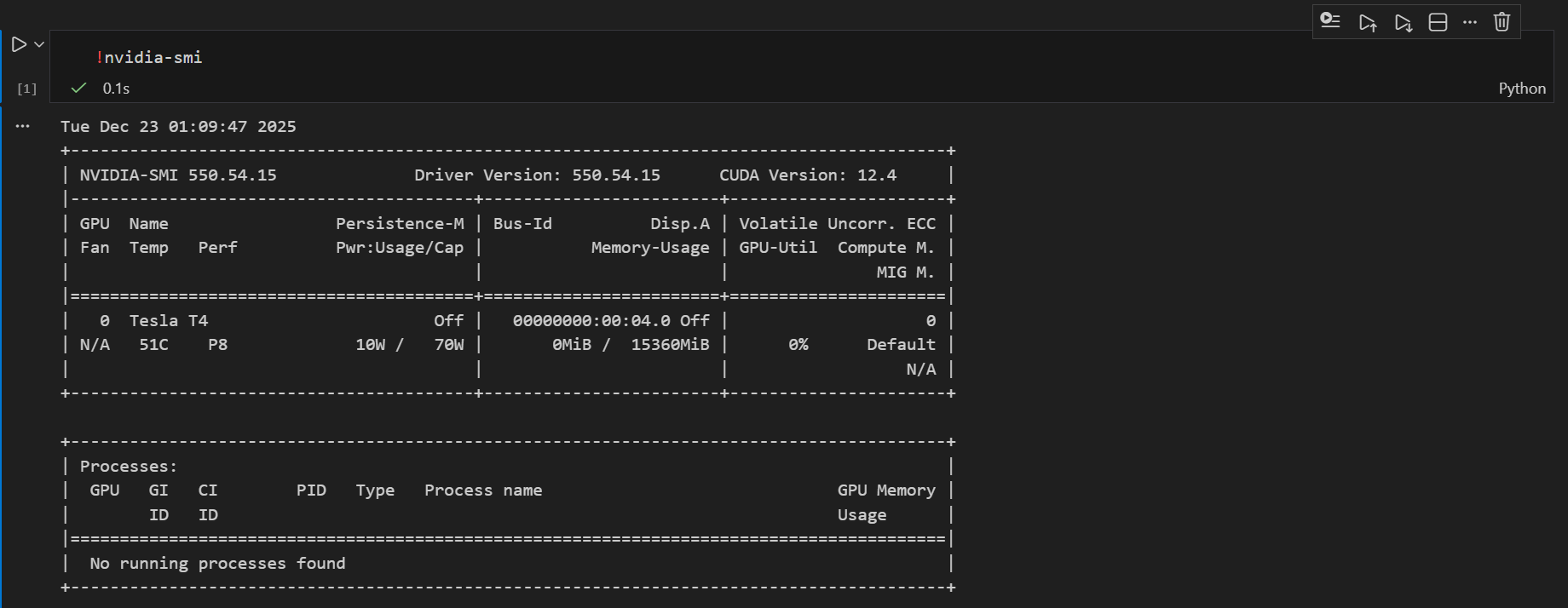
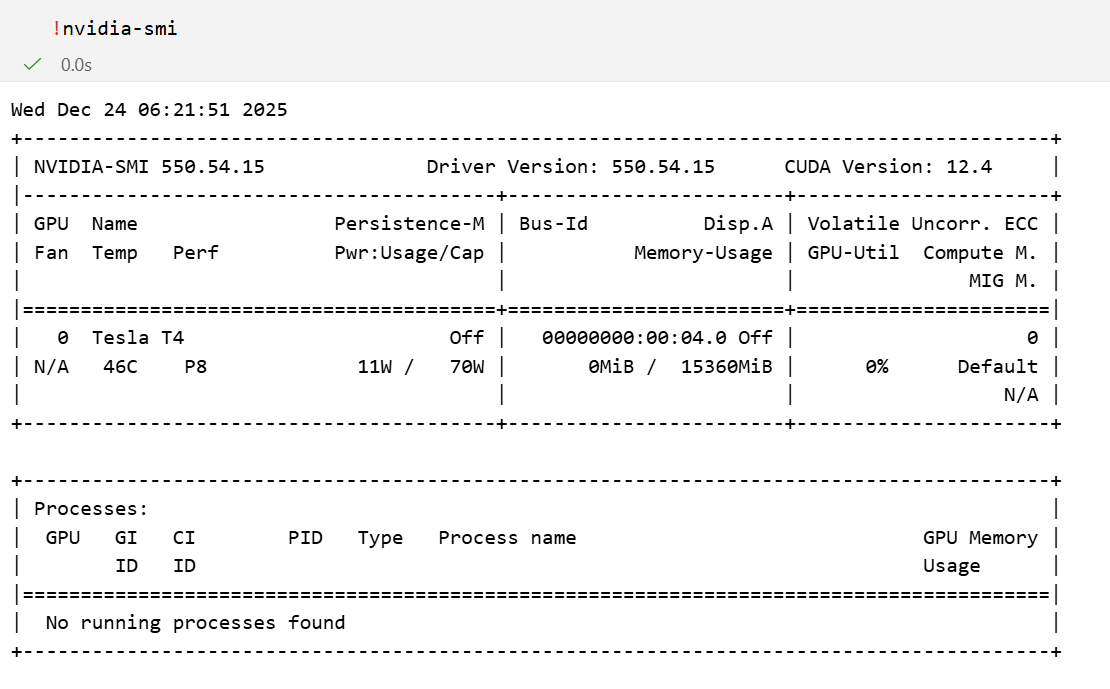
下面是一个标准的 nvidia-smi (NVIDIA System Management Interface) 输出界面。它展示了当前 GPU 的状态、驱动版本以及运行的进程。
具体查看,可以参考我上一篇博客:nvidia-smi输出界面
创建数据集

然后这里需要用到一个模拟的螺旋数据集,正好用到我们前面在前言中提到的nnfs库。
nnfs库中的一个数据集,对应函数是spiral_data
这个函数的来源是斯坦福计算机视觉课CS231n的一个case-study,
https://cs231n.github.io/neural-networks-case-study/
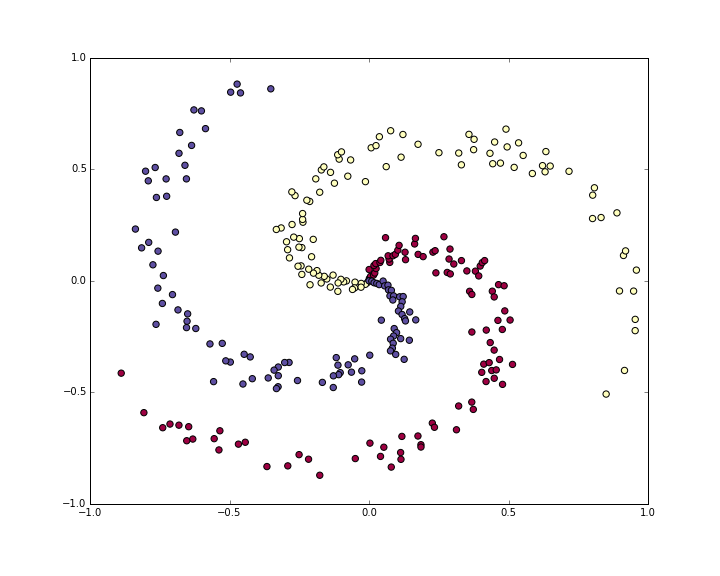
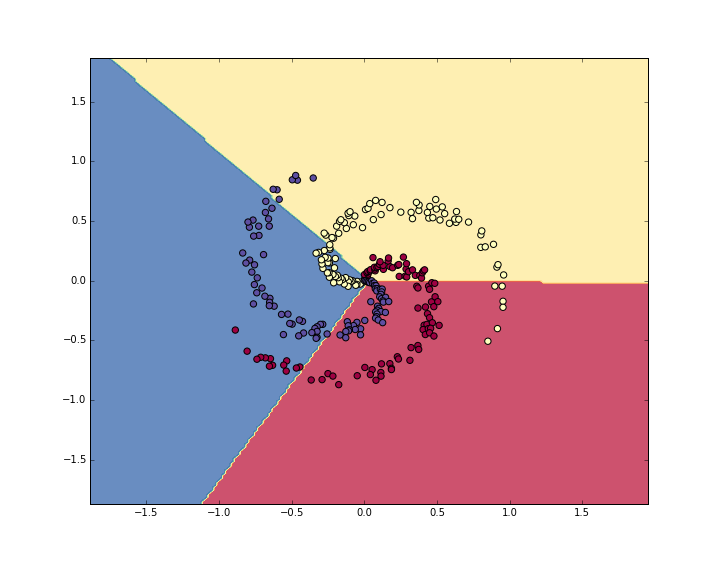
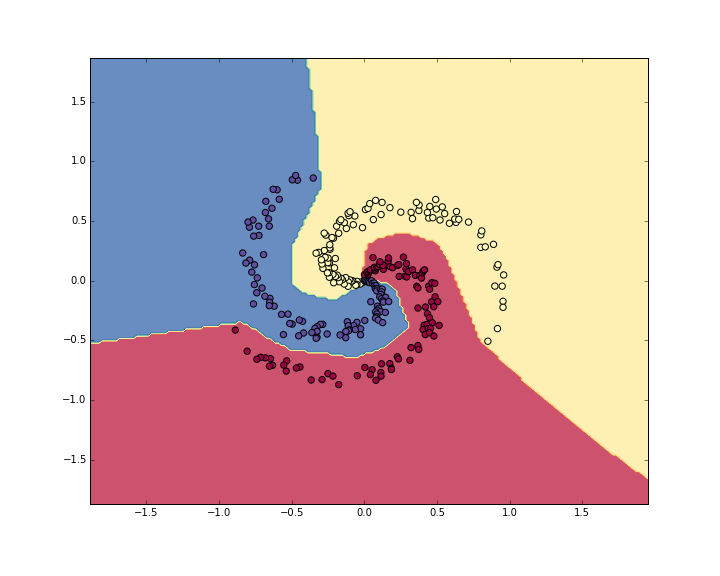
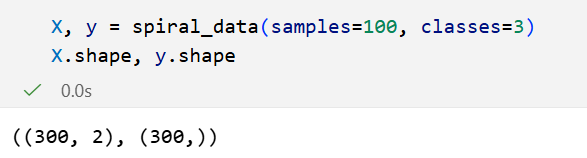
总的来说就是3个螺旋,每一个螺旋100个样本点。总共300个样本,x是训练数据,y是label。
然后X总共就两个feature,X[:, 0], X[:, 1]分别作为二维坐标。
这个问题其实是一个很经典的机器学习的分类问题,
如果是用传统机器学习,我们可以从训练一个线性分类器出发,再拓展到非线性分类器。
比如说LDA、QDA、朴素贝叶斯,SVM,决策树等等等等。
当然,我们这里讲的是深度学习,当然用的也就是神经网络的方法了。
看一下第5个样本点,以及其label(class 0)
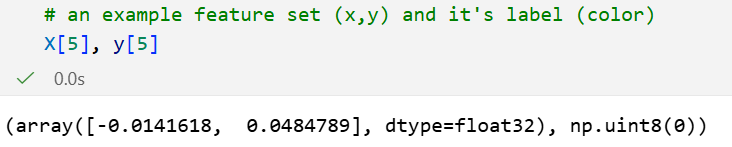
实例化模型

softmax这里,做的功能一般是归一化,严格来说softmax是输出层的归一化函数而非典型激活函数。
毕竟只是归一化概率,并没有抑制什么信息。
但学界常将其归类为"输出层激活函数"有两大原因,在多分类网络中替代了sigmoid/tanh的末端角色,将线性输出转化为概率分布;与交叉熵损失结合时能构建有效的梯度传播路径。实际应用中需明确其定位,当问题涉及"隐藏层用什么激活函数"时(如ReLU/GELU),softmax不在讨论范围内;但若泛指"模型末端映射函数",可将其视为激活函数。
简单来说就是,很多不是很严谨的论文中会在模型模块将softmax和激活函数字眼联系在一起。
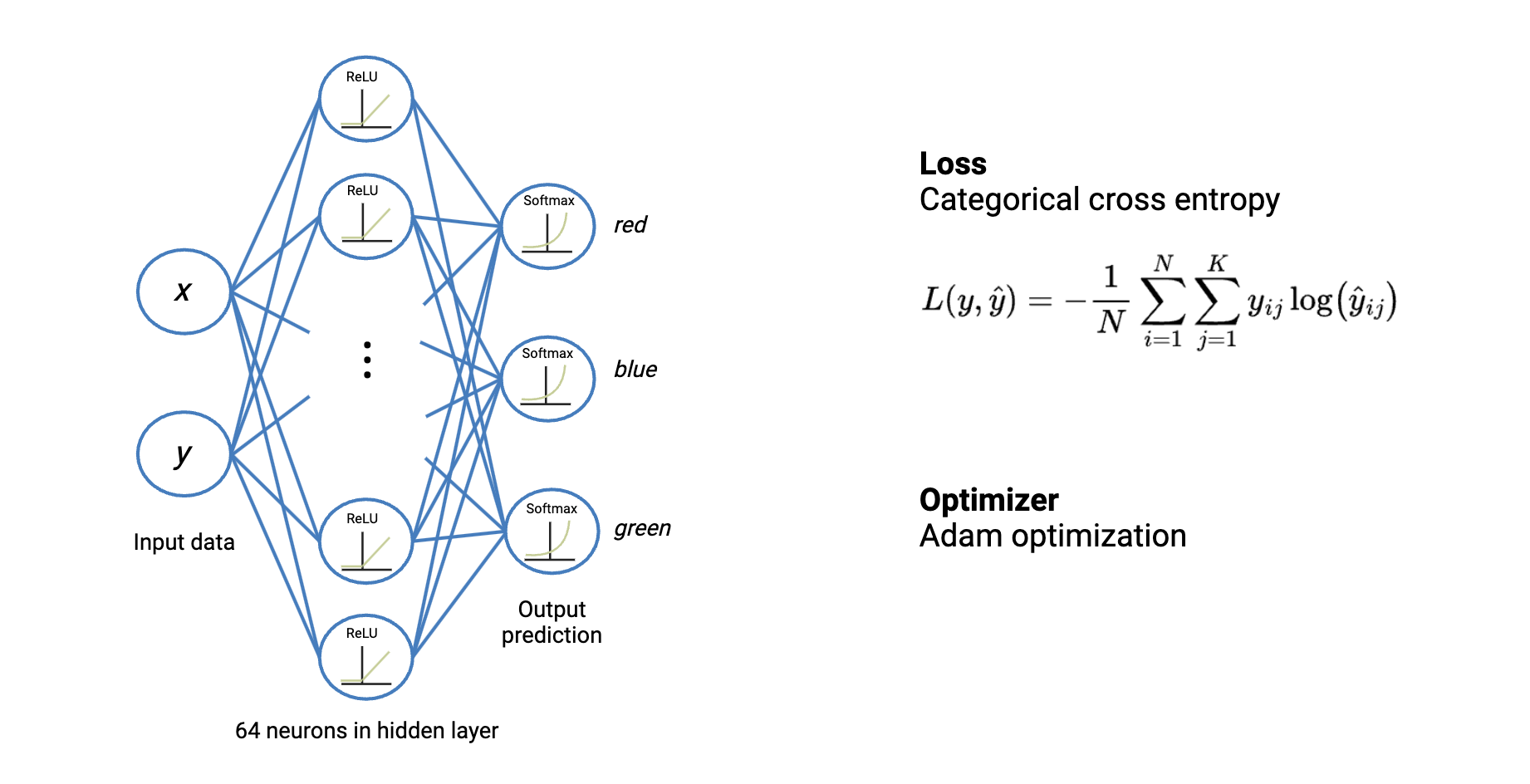 上面的这个图绘制的有点视觉误导,我觉得应该按照下面的视觉效果:
上面的这个图绘制的有点视觉误导,我觉得应该按照下面的视觉效果:

画成这样才不容易被误导:
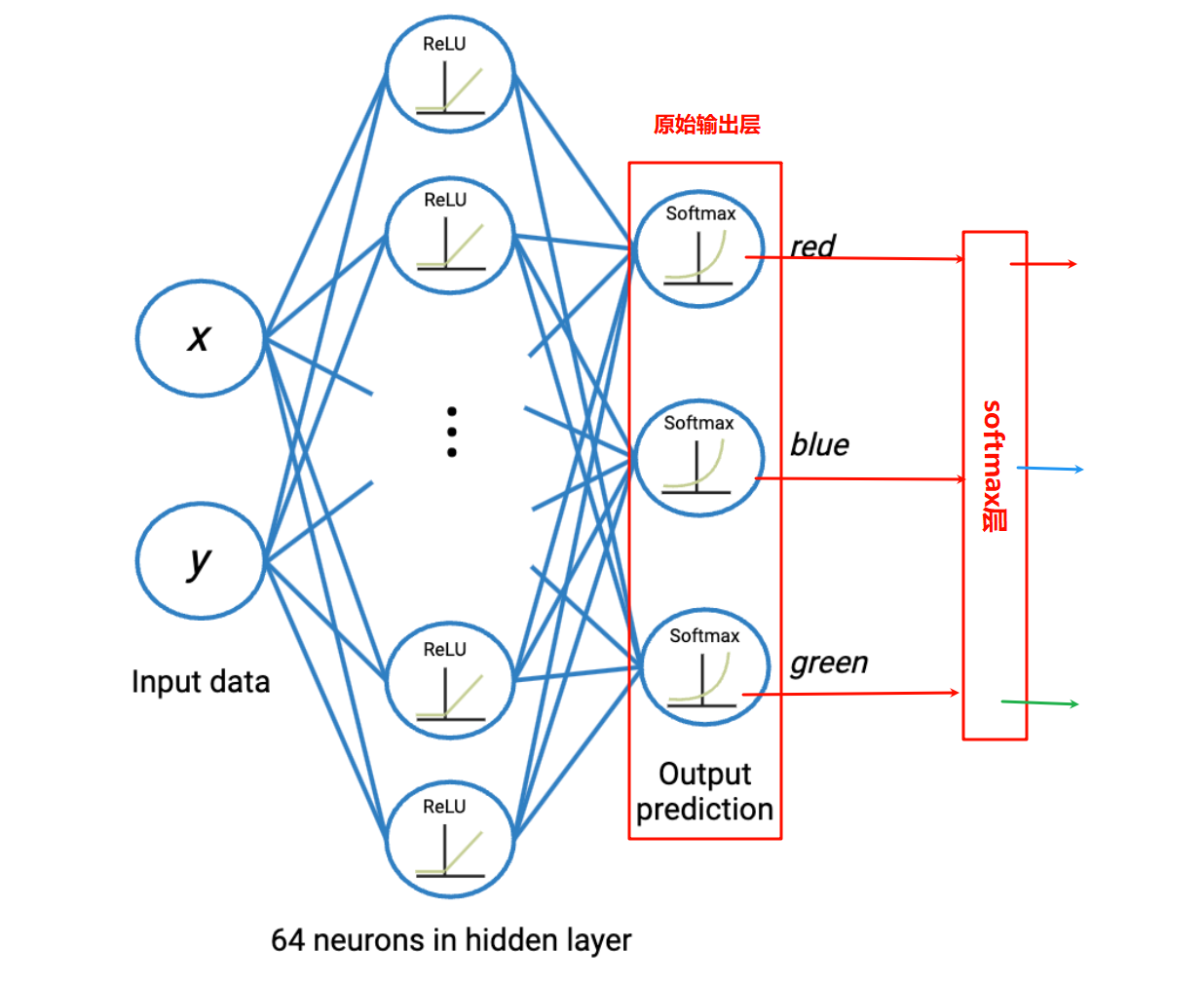
前面我们的数据x是(300,2)二维tensor,y是(300,)一维tensor;
300个样本点,我们以1个样本点为例,比如说xi,yi,
那就是(1,2)的数据和(1,)的label。
那么数据流可以这么理解:
样本点xi,形状shape是(1,2)。
- 输入层:(1,2),也就是样本点
- Dense1(隐藏层1/全连接层1):
- 权重矩阵是(2,64)
- 运算:(1,2)dot (2,64)------》(1,64)
- ReLU激活函数:将这64个数里面小于0的变成0,也就是未激活,shape依然是(1,64)
- Dense2(隐藏层2/全连接层2):
- 权重矩阵是(64,3),因为输出层是3个神经元,对应3个类别的输出预测,有3套不同的权重+bias的参数集
- 运算:(1,64)dot (64,3)------》(1,3)
- softmax层
- 输入是(1,3)的得分
- 输出是(1,3)的概率分布(和为1)
- Loss计算
- 拿这3个概率(也就是(1,3)输出的3个分量)去和真实的标签做对比,计算误差
10,只使用Numpy构建的1个简单全连接网络全代码
真纯Numpy手搓1个简单的神经网络
不借助pytorch、tensorflow等现代框架,
纯靠numpy,我们就能够手搓一个简单的神经网络;
逻辑很简单,我们将神经网络(此处指MLP)当做是一个算法问题,
从数学角度我们能够理解流程逻辑,从代码角度我们能够规划好数据输入输出流,
所以我们绝对能够纯手工搓1个简单的神经网络出来。
这里强调一下,手搓神经网络,并不是为了自找苦吃,而是为了让我们能够更加深入地理解神经网络的数学、代码逻辑,只有吃透了最简单、最原始的模块,我们之后遇到再复杂的网络、再复杂的结构,
都不会再吓到。
因为我们已经能够手搓1个最简单的系统(还原论的本质),再复杂也只是模块封装的表象。
下面就是一个多分类的神经网络model,去掉注释,其实核心也就500行以内。
具体衍生,我会在下一篇博客中展开。
python
import numpy as np
# =============================================================================
# 第一部分:底层核心类库
# =============================================================================
# 1. 全连接层
class Layer_Dense:
def __init__(self, n_inputs, n_neurons):
"""
Description
-----------
初始化全连接层的权重和偏置, 注意这是一个抽象的全连接层类, 不是输入层!
Args
----
n_inputs : int
当前层输入特征的数量(例, 输入28x28图像, 则n_inputs=784, 就是feature维度)
n_neurons : int
当前层输入神经元的数量
Notes
-----
- 1, 解释: 输入层数据格式是「样本 x 特征(n_samples, n_features), 隐藏层核心是「神经元数量(n_neurons), 权重矩阵用「特征 x 神经元(n_features, n_neurons)」的维度设计,正是为了通过矩阵乘法让两者高效衔接;
输入数据形状是 (n_samples, n_features)(比如 100 个样本, 每个样本 784 个特征 → (100, 784)),权重矩阵是 (n_features, n_neurons)(784 个特征 x 10 个神经元 → (784, 10));
(n_samples, n_features) @ (n_features, n_neurons) = (n_samples, n_neurons)
- 2, 当前全连接层单层的构建未涉及激活函数, 只是单纯的线性变换(矩阵乘法+偏置), 激活函数会在后续单独实现, 所以所有的output都是线性变换的结果, 我们直接考虑loss计算和反向传播即可, 不需要考虑激活函数的非线性影响, 就是将output作为当前层的最终输出(类比激活函数之后的输出)
"""
# 初始化(n_inputs, n_neurons)形状的权重矩阵, 采用随机的标准正态分布
# 缩放0.01以防止权重过大, 避免前向传播时输出过大导致梯度消失/爆炸
self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
# 初始为(1, n_neurons)形状的全0偏置向量, 每个神经元对应一个偏置值
# 每个神经元只有 1 个偏置(管 "神经元的偏移");所有样本共享这组偏置(管 "规则通用")
# 偏置的本质是 "与样本无关的神经元偏移",所有样本共享同一组偏置(1 个神经元 1 个偏置)
# 偏置的第 2 维(神经元数)必须和「输入 × 权重」结果的第 2 维(神经元数)完全一致(比如都是 10)------ 因为要给每个神经元加专属偏移,维度不匹配就加错了;
# 偏置的第 1 维(样本数)用 1,是因为广播机制会自动把 1 扩展成实际样本数(比如 100)------ 既满足 "所有样本共享偏置",又避免存储冗余(不用存 100 份重复的偏置)。
# 所以这里偏置形状是 (1, n_neurons), 而不是反过来(n_neurons, 1)
self.biases = np.zeros((1, n_neurons))
def forward(self, inputs):
"""
Description
-----------
前向传播, 计算当前层的输出(输入的线性变换)
Args
----
inputs : np.ndarray
输入数据, 上一层的输出, 形状为(上一层输出样本数, 上一层输出特征数), 也就是(n_samples, n_inputs/features)
Notes
-----
- 1, forward方法依然是在前面整体抽象的全连接层中定义的,不特指输入层到第一层隐藏层, 而是可以作为任意两层之间的全连接层;
只能说是当前层, 无论是哪一层, 全连接层的输出形状都是 (n_samples, 上一层神经元数);
不管是输入层后的第一层,还是隐藏层之间,只要传入符合维度的 inputs(上一层输出/上一层神经元数/当前层输入feature数), 并提前定义好对应维度的 weights(n_in_features x 当前层神经元数)和 biases(1 x 当前层神经元数),就能自动完成前向传播计算。
- 2, 理解抽象全连接层中inputs的维度:
- 通用维度: inputs.shape = (样本数, 当前层输入特征数),与层位置无关;
- 样本数不变:所有层的 inputs 第一维度都是同一批样本数,贯穿网络;------》从矩阵乘法角度来看, 任意中间层的行数=第1个矩阵的行数
- 输入特征数来源:当前层的 "输入特征数" = 上一层的输出特征数 = 上一层的神经元数量;
- 抽象复用性:正因为维度规则通用,这个 forward 方法才能作为任意全连接层使用,只需匹配上一层输出和自身权重维度即可
- 3, 此处的全连接层不包括激活函数, 只是单纯的线性变换(矩阵乘法+偏置), 激活函数会在后续单独实现, 所以所有的output都是线性变换的结果, 我们直接考虑loss计算和反向传播即可, 不需要考虑激活函数的非线性影响, 就是将output作为当前层的最终输出(类比激活函数之后的输出)
"""
# 保存当前层的输入, 用于后续反向传播计算梯度
self.inputs = inputs
# 计算当前层的输出: output = inputs @ weights + biases (矩阵乘法+广播机制)
# 输入数据 X:100 个样本,每个样本 784 个特征 → 形状 (100, 784);
# 权重 weights:784 个特征 × 10 个神经元 → 形状 (784, 10);------》X @ weights → 形状 (100, 784) @ (784, 10) = (100, 10)
# 偏置 biases:1 行 × 10 个神经元 → 形状 (1, 10)(全 0 初始化,即 [[0,0,0,...,0]])。------》NumPy 的广播机制会自动把 (1,10) 的偏置 "复制扩展" 成 (100,10)
# 刚好实现了 "给每个神经元的所有样本输出,都加同一个偏移量"------ 这正是 "与样本无关、每个神经元 1 个偏置"
self.output = np.dot(inputs, self.weights) + self.biases
def backward(self, dvalues):
"""
Description
-----------
反向传播, 计算当前层的梯度 (更新梯度值用于优化器更新参数)
Args
----
dvalues : np.ndarray
下一层传递过来的梯度, 损失对当前层输出的偏导, 作为当前层需要计算梯度的起点;
dvalues(当前层梯度起点) = ∂L(整体loss)/∂out(当前层输出, 也就是下一层输入)
Notes
-----
- 1, 我们这里的表述是下一层(靠近output)传到上一层(靠近input), 从loss传到输入的反向顺序说法, 所谓的上下是按照正常正向数据传递的说法表述
- 2, 对于矩阵微积分求导部分的数学符号以及规则说明, 可以参考: https://blog.csdn.net/weixin_62528784/article/details/156519242?spm=1001.2014.3001.5501
"""
# 计算权重的梯度:损失对权重的偏导 = 输入的转置 @ 下一层梯度
# 原理: 依据链式法则, ∂L/∂W = ∂L/∂out * ∂out/∂W
# 其中 ∂out/∂W = inputs.T, 因为 out = inputs @ weights + biases------》这一点可以从矩阵求导的分母布局法理解(输入的转置的形状正好和权重形状匹配)
# 而 ∂L/∂out 就是 dvalues, 因为 dvalues = ∂L/∂out, dvalues就是定义为loss对这一层输出的梯度, 所以dvalues是我们计算的起点
self.dweights = np.dot(self.inputs.T, dvalues)
# 计算偏置的梯度:损失对偏置的偏导 = 下一层梯度的求和(下一层沿样本轴求和)
# 原理: 依据链式法则, ∂L/∂b = ∂L/∂out * ∂out/∂b
# 其中 ∂out/∂b = 1 (因为偏置是加法项, 对每个样本都一样), 因为 out = inputs @ weights + biases
# 所以 ∂L/∂b = sum(∂L/∂out) = sum(dvalues)
# keepdims=True保持维度为(1, n_neurons),与偏置形状一致
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# 计算输入的梯度:损失对输入的偏导 = 下一层梯度 @ 权重的转置
# 原理: 依据链式法则, ∂L/∂inputs = ∂L/∂out * ∂out/∂inputs
# 其中 ∂out/∂inputs = weights.T, 因为 out = inputs @ weights + biases ------》和前面一样可以从矩阵求导的分母布局法理解(权重的转置的形状正好和输入形状匹配)
# 而 ∂L/∂out 就是 dvalues, 因为 dvalues = ∂L/∂out
# 所以 ∂L/∂inputs = dvalues @ weights.T
# 原理: 将梯度反向传给上一层, 用于前一层的参数更新
self.dinputs = np.dot(dvalues, self.weights.T)
# 2. ReLU 激活函数
class Activation_ReLU:
"""
Description
-----------
ReLU(Rectified Linear Unit) 激活函数
用于引入非线性, 解决线性模型无法拟合复杂数据的问题
Notes
-----
- 1, 此处单独实现ReLU激活函数类, 作为独立的激活层使用, 不考虑与全连接层耦合
"""
def forward(self, inputs):
"""
Description
-----------
前向传播, 计算ReLU激活函数的输出(out_relu)
Args
----
inputs : np.ndarray
in_relu, 输入数据, 上一层的输出, 全连接层的线性输出, 形状与全连接层输出一致, 也就是不考虑与激活函数耦合时的全连接层输出;
Notes
-----
- 1, 理论上全连接层输出inputs+本层激活函数之后的输出才是当前层的最终输出, 但由于此处不考虑耦合, 此处只是独立的1个激活层, 所以直接将ReLU的输出作为当前层的最终输出
"""
# 保存当前层的输入(in_relu), 用于后续反向传播判断梯度是否为0
self.inputs = inputs
# 计算ReLU激活函数的输出(out_relu): output = max(0, inputs), ReLU函数将负值置0, 保持正值不变
self.output = np.maximum(0, inputs)
def backward(self, dvalues):
"""
Description
-----------
反向传播, 计算ReLU激活函数的梯度, 用于更新前一层的梯度(ReLU层链式法则传递),
计算公式: ∂L/∂in_relu = ∂L/∂out_relu * ∂out_relu/∂in_relu
Args
----
dvalues : np.ndarray
out_relu, 下一层传递过来的梯度, 损失对当前层输出的偏导, 也就是损失对ReLU层输出的偏导, 作为当前层需要计算梯度的起点;
dvalues(当前层梯度起点) = ∂L(整体loss)/∂out(当前层输出, 也就是下一层输入)
Notes
-----
- 1, ReLU层在反向传播时的核心任务:
- 接收下一层传递过来的梯度 dvalues = ∂L/∂out_relu (损失对ReLU层输出的偏导);
- 计算当前层的梯度 dinputs = ∂L/∂in_relu (损失对ReLU层输入的偏导), 传递给前一层用于更新梯度;
- 将调整后的梯度传递给上一层(通常是全连接层), 供上一层计算参数(权重/偏置)的梯度;
- 依据ReLU的梯度规则调整梯度值(输入<=0位置的梯度置0, 输入>0位置的梯度保持不变);
- 2, 激活函数层都是剥离开来, 单独实现的, 上一个全连接层的输出作为当前ReLU层的输入, 当前ReLU层的输出作为下一个全连接层的输入;
"""
# 复制下一层传递过来的梯度, 作为当前层的梯度初始值
# 若ReLU层后接全连接层, 则dvalues就是全连接层backward方法计算出的self.dinputs(全连接层的输入梯度, 对应ReLU层的输出梯度)
# 为什么复制? 因为我们需要修改梯度值, 不能直接修改传入的dvalues, 因为下一层的梯度结果dvalues可能还会被其他层使用
# 这样可以避免影响到其他层的梯度计算
# ReLU的梯度计算需要根据输入值是否大于0来决定(也就是需要基于自身输入调整)
self.dinputs = dvalues.copy()
# ReLU的梯度规则: 当输入值<=0时, 梯度为0; 当输入值>0时, 梯度保持不变, 为1
# 此处self.inputs就是ReLU层的输入值(in_relu), 要计算其梯度, ∂L/∂in_relu = ∂L/∂out_relu * ∂out_relu/∂in_relu
# - 当in_relu <= 0, 也就是 self.inputs <= 0, 则 ∂out_relu/∂in_relu = 0, 因为ReLU函数在该区间的梯度为0 ------> 整体梯度 ∂L/∂in_relu = ∂L/∂out_relu * 0 = 0, 即把self.dinputs对应位置置0
# - 当in_relu > 0, 也就是 self.inputs > 0, 则 ∂out_relu/∂in_relu = 1, 因为ReLU函数在该区间的梯度为1 ------> 整体梯度 ∂L/∂in_relu = ∂L/∂out_relu * 1 = ∂L/∂out_relu, 即self.dinputs保持不变
# 因此我们需要将输入值<=0的位置的梯度置0, 不传递该位置的梯度
self.dinputs[self.inputs <= 0] = 0
# 3. Softmax 激活函数 (用于预测)
class Activation_Softmax:
"""
Description
-----------
softmax激活函数层, 用于多分类任务的输出层, 将线性输出转化为概率分布
Notes
-----
- 1, 本类中未实现反向传播, 通常与交叉熵损失结合使用, 以简化反向传播计算
"""
def forward(self, inputs):
"""
Description
-----------
前向传播, 计算Softmax激活函数的输出概率分布, 计算公式: softmax(xi) = exp(xi) / sum(exp(xj))
Args
----
inputs : np.ndarray
输入数据, 上一层的输出, 全连接层的线性输出, 形状与全连接层输出一致, 简单理解为in_softmax;
输出层全连接层的线性输出, 称为Logits, 形状为(样本数, 类别数)
output : np.ndarray (在状态中保存)
softmax激活函数的输出概率分布, 形状与输入一致, (样本数, 类别数);
inputs是softmax层输入, output是softmax层输出
"""
# 保存当前层的输入, 用于后续计算(反向传播时需要用到, 本类中未实现反向传播, 通常与交叉熵损失结合)
self.inputs = inputs
# step1: 为了数值稳定性, 减去每行(每个样本)的最大值, 防止指数函数溢出(np.exp过大可能返回inf)
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# step2: 计算每行(每个样本)的指数和, softmax概率=每个样本的指数值/该样本所有指数值的和
self.output = exp_values / np.sum(exp_values, axis=1, keepdims=True)
# 4. 通用 Loss 父类
class Loss:
"""
Description
-----------
定义损失函数的统一接口, 所有具体损失函数类均继承自该父类
"""
def calculate(self, output, y):
"""
Description
-----------
计算损失的公共方法: 返回平均损失(数据损失)
Args
----
output : np.ndarray
模型的预测输出, 形状为(样本数, 类别数)
y : np.ndarray
真实标签, 可为类别索引或独热编码, 对应形状为(样本数,)或(样本数, 类别数) (独热编码)
"""
# 调用子类实现的forward方法, 计算每个样本的损失(样本损失)
# 调用具体损失函数的前向传播方法, 计算每个样本的损失, forward方法在子类中具体实现, 父类中只是定义抽象接口
sample_losses = self.forward(output, y)
# 计算所有样本的平均损失(数据损失), 作为模型优化的目标
data_loss = np.mean(sample_losses)
return data_loss
# 5. 交叉熵损失 (含 Softmax)
class Loss_CategoricalCrossentropy(Loss):
"""
Description
-----------
交叉熵损失函数, 用于多分类任务, 与softmax配合使用
Args
----
继承自 Loss 父类, 实现具体的前向和反向传播方法
"""
def forward(self, y_pred, y_true):
"""
Description
-----------
前向传播, 计算每个样本的交叉熵损失
Args
----
y_pred : np.ndarray
模型的预测输出概率, 形状为(样本数, 类别数), softmax层的输出概率
y_true : np.ndarray
真实标签, 可为类别索引或独热编码, 对应形状为(样本数,)或(样本数, 类别数) (独热编码)
"""
# 获取样本数量, 用于后续平均损失计算
samples = len(y_pred)
# 防止log(0)导致数值不稳定, 对预测概率进行裁剪
# 裁剪范围在[1e-7, 1-1e-7]之间
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# 从模型输出的概率矩阵 y_pred_clipped 中,提取每个样本「真实类别对应的预测概率」
# 用于后续计算交叉熵损失: -log(正确类别的预测概率)
# 分两种情况处理真实标签: 类别索引或独热编码
# case1: 真实标签为类别索引 (一维数组), 如 y_true = [0, 2, 1] 其shape为(3,)
if len(y_true.shape) == 1:
# 列表索引取出每个样本对应的正确类别的预测概率
# 前面提到过, 列表索引index是按位置配对取元素
correct_confidences = y_pred_clipped[range(samples), y_true]
# case2: 真实标签为独热编码 (二维数组), 如 y_true = [[1,0,0], [0,0,1], [0,1,0]]
elif len(y_true.shape) == 2:
# 通过逐元素相乘并沿类别轴求和, 获取每个样本对应的正确类别的预测概率
# 注意 * 就是逐元素乘法, 就是线性代数中的Hadamard积, 哈达玛乘积(维度相同)
# np.dot 或 @ 是矩阵乘法
# 预测概率与独热编码逐元素乘法, 等价于取真实类别的概率(独热编码只有真实类别为1)
correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)
# correct_confidences中保存了每个样本「真实类别对应的预测概率」, 形状为(samples,)
# 计算交叉熵损失: -log(正确类别的预测概率)
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
def backward(self, dvalues, y_true):
"""
Description
-----------
反向传播, 计算损失对模型输出y_pred的梯度, 记为∂L/∂y_pred, 并将结果存入self.dinputs, 最终传递给前一层(通常是输出层的全连接层, 当然最后一层一般是softmax层),
用于后续参数(权重, 偏置)的梯度计算和更新
Args
----
dvalues : np.ndarray
下一层传递过来的梯度, 损失对当前层输出的偏导;
dvalues(当前层梯度起点) = ∂L(整体loss)/∂out(当前层输出, 也就是下一层输入);
当然, 在此处独立的交叉熵损失层中, dvalues其实就是y_pred, 因为损失层是网络的最后一层, 没有更下游的层了, 所以dvalues就是损失对y_pred的偏导的起点;
即损失计算的输入, 也就是模型的预测输出y_pred
y_true : np.ndarray
真实标签, 可为类别索引或独热编码, 对应形状为(样本数,)或(样本数, 类别数) (独热编码)
Notes
-----
- 1, 公式推导的是「单个样本的梯度」,但代码中计算的是所有样本的平均梯度(因损失 L 通常取平均值),因此需要除以样本数
- 2, 该层中的dvalues其实就是y_pred, dinputs就是损失对y_pred的梯度, 也就是∂L/∂y_pred
"""
# 获取样本数和类别数
# 注意此处dvalues就是y_pred(模型的预测输出), 因为交叉熵损失层是最后一层, 没有更下游的层了
samples = len(dvalues)
labels = len(dvalues[0])
# 如果输入是类别索引, 则转换为独热编码形式
if len(y_true.shape) == 1:
# np.eys(label)生成单位矩阵,y_true作为索引取出对应行, 即独热编码
# np.eye(labels):生成 (类别数, 类别数) 的单位矩阵(对角线上为 1,其余为 0), 每行对应1个类别的独热编码
# [y_true]:用真实类别索引取单位矩阵的对应行,得到独热编码形式
y_true = np.eye(labels)[y_true]
# 交叉熵损失对y_pred的梯度公式: -真实标签/预测概率
# 计算公式为 ∂L/∂y_pred = ∂(-sum(y_true * log(y_pred)))/∂y_pred
# 一般为了计算方便, log的底数取e, 其实就是ln, 求导就是1/x
# 然后我们以样本的某一个类别为例子来推导:
# L = -y_true * log(y_pred), 对y_pred,c求导:
# ∂L/∂y_pred,c = ∂(-sumk(y_true,k * log(y_pred,k)))/∂y_pred,c
# 只有当k=c时, 导数不为0, 其他k≠c时导数为0, 所以:
# ∂L/∂y_pred,c = -y_true,c/y_pred,c
# 推广到所有类别, 就是 ∂L/∂y_pred = -y_true / y_pred
self.dinputs = -y_true / dvalues
# 归一化梯度, 除以样本数, 保持梯度规模稳定(确保梯度规模与样本数量无关)
self.dinputs = self.dinputs / samples
# 6. Softmax + Loss 组合类 (为了反向传播更稳定)
class Activation_Softmax_Loss_CategoricalCrossentropy():
"""
Description
-----------
将softmax激活函数与交叉熵损失结合, 优化反向传播稳定性;
因为单独计算softmax和交叉熵的梯度会有数值不稳定问题, 组合后可简化梯度计算
Notes
-----
- 1, 该类封装了softmax激活和交叉熵损失, 提供前向和反向传播方法, 具体调用类的实现细节见前面softmax和交叉熵损失类
"""
def __init__(self):
"""
Description
-----------
初始化组合类, 创建softmax激活和交叉熵损失实例
"""
# 实现见前面
# softmax激活层
self.activation = Activation_Softmax()
# 交叉熵损失层
self.loss = Loss_CategoricalCrossentropy()
def forward(self, inputs, y_true):
"""
Description
-----------
前向传播, 计算softmax输出和交叉熵损失(先激活再计算损失)
Args
----
inputs : np.ndarray
输入数据, 上一层的输出, 全连接层的线性输出, 形状与全连接层输出一致;
输出层全连接层的线性输出, 称为Logits, 形状为(样本数, 类别数),
也就是in_softmax, softmax层的输入
y_true : np.ndarray
真实标签, 可为类别索引或独热编码, 对应形状为(样本数,)或(样本数, 类别数) (独热编码), 同交叉熵损失
"""
# 对Logits做softmax激活, 得到概率分布
# 也就是Activation_Softmax()类的forward方法
self.activation.forward(inputs)
# 保存激活后的输出(概率分布), 用于后续反向传播
# 也就是softmax激活函数的输出概率分布, 形状与输入一致, (样本数, 类别数);
# inputs是softmax层输入, output是softmax层输出
self.output = self.activation.output
# 计算平均交叉熵损失,调用交叉熵损失的calculate方法
# 实际实现细节上调用的是Loss_CategoricalCrossentropy类的forward方法, 也就是将softmax层的输出作为输入计算损失
return self.loss.calculate(self.output, y_true)
def backward(self, dvalues, y_true):
"""
Description
-----------
反向传播, 计算组合层的梯度, 直接计算简化后的梯度公式(也就是直接计算损失对Logits的梯度, 避免数值不稳定)
Args
----
dvalues : np.ndarray
下一层传递过来的梯度, 损失对当前层输出的偏导;
dvalues(当前层梯度起点) = ∂L(整体loss)/∂out(当前层输出, 也就是下一层输入);
当然, 在此处softmax+交叉熵组合层中, dvalues其实就是y_pred, 因为组合层是网络的最后一层, 没有更下游的层了, 所以dvalues就是损失对y_pred的偏导的起点;
即损失计算的输入, 也就是模型的预测输出y_pred
y_true : np.ndarray
真实标签, 可为类别索引或独热编码, 对应形状为(样本数,)或(样本数, 类别数) (独热编码)
Notes
-----
- 1, 注意该组合层backward的目标是计算损失对Logits的梯度(也就是损失对全连接层输出的梯度), 以便传递给前一层(通常是输出层的全连接层), 用于更新参数;
也就是计算 ∂L/∂Logits, 而不是单独计算softmax层或交叉熵损失层的梯度;
"""
# 获取样本数量
# 注意这里的dvalues就是y_pred(模型的预测输出), 因为softmax+交叉熵组合层是最后一层, 没有更下游的层了
samples = len(dvalues)
if len(y_true.shape) == 2:
# 若真实标签为独热编码, 则转换为类别索引(方便后续索引操作), 独热变索引
y_true = np.argmax(y_true, axis=1)
# 复制dvalues(此处dvalues是softmax的输出, 即概率分布), 因为y_pred可能有其他作用, 比如说计算准确率等, 不能直接修改
self.dinputs = dvalues.copy()
# 关键步骤:简化之后的梯度也就是softmax+交叉熵的联合梯度 = 预测概率 - 真实标签(独热编码形式)
# 对每个样本的 "真实类别对应的概率" 减 1, 等价于将独热编码的 y_true 中 "1" 的位置减 1, "0" 的位置不变
# 用的还是列表索引
self.dinputs[range(samples), y_true] -= 1
# 梯度归一化: 除以样本数, 保持梯度规模稳定(确保梯度规模与样本数量无关)
self.dinputs = self.dinputs / samples
# 7. Adam 优化器
class Optimizer_Adam:
"""
Description
-----------
Adam优化器类, 用于更新神经网络的权重和偏置参数, 结合动量(Momentum)和自适应学习率(RMSProp)的优化算法, 通过积累历史梯度信息动态调整参数更新策略,实现更快收敛和更稳定的训练;
收敛快, 稳定, 适合大多数神经网络训练
Adam的核心是维护两个关键变量:
- 动量(momentum): 积累历史梯度的"方向", 缓解SGD在局部最优附近的震荡, 加速沿稳定方向的收敛;量纲是"梯度的累积", 梯度是损失对参数的偏导, 量纲是损失值/参数值
- 自适应缓存(cache): 积累历史梯度的"幅度", 为每个参数动态调整学习率(梯度大的参数用小步长, 梯度小的参数用大步长);量纲是"梯度平方的累积", 量纲是(损失值/参数值)^2
其中偏差修正: 初始阶段动量和缓存接近0, 通过修正项使其更接近真实值, 避免初期更新过慢
注意, 优化器维护的动量和缓存只是辅助变量, 与此处model的权重/偏置核心参数不同;
辅助变量的初始化≠核心参数的初始化
"""
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
"""
Description
-----------
初始化Adam优化器的超参数
Args
----
learning_rate : float
初始学习率, 控制参数更新的步长大小, 默认0.001
decay : float
学习率衰减率, 控制学习率随迭代次数逐渐减小, 默认0.0(不衰减)
epsilon : float
防止除0错误的小常数, 用于数值稳定性, 默认1e-7
beta_1 : float
动量项的指数衰减率(控制动量的历史贡献, 默认0.9)
beta_2 : float
自适应学习率项的指数衰减率(控制平方梯度的历史贡献, 默认0.999)
"""
# 初始学习率, 即初始步长, 控制参数更新的幅度
self.learning_rate = learning_rate
# 当前学习率(可能会随迭代次数逐渐衰减), 实际用于更新的学习率
self.current_learning_rate = learning_rate
# 学习率衰减率(控制实际用于更新的学习率随迭代次数减小, 避免后期震荡), 默认0不衰减
self.decay = decay
# 迭代次数(用于学习率衰减计算和偏差修正)
self.iterations = 0
# 防止除0错误的小常数, 数值稳定项
self.epsilon = epsilon
# 动量项系数, 控制动量的历史贡献; 即动量项的指数衰减率, 控制历史动量的"记忆比例"(β1越大, 记忆越久)
self.beta_1 = beta_1
# 自适应学习率项系数, 控制平方梯度的历史贡献; 即自适应学习率项/缓存项的指数衰减率, 控制历史平方梯度的"记忆比例"(β2越大, 记忆越久)
self.beta_2 = beta_2
def pre_update_params(self):
"""
Description
-----------
在更新参数前调用, 用于调整当前学习率(如果设置了衰减);
在每次参数更新之前, 根绝迭代次数调整当前学习率(current_learning_rate), 仅当decay>0时生效
"""
if self.decay:
# 若启动学习率衰减, 则根据迭代次数调整当前学习率/按公式更新当前学习率
# 衰减公式: lr = initial_lr / (1 + decay * iterations)
# 训练前期, 迭代次数小, 当前学习率接近初始值, 大步长快速收敛; 训练后期, 迭代次数大, 当前学习率减小, 小步长精细调整参数, 避免在最优解附近震荡
# 目的: 训练前期使用较大学习率快速收敛, 后期使用较小学习率精细调整
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
def update_params(self, layer):
"""
Description
---------
接收1个全连接层(Layer_Dense示例), 利用该层的梯度(dweights/dbiases)更新其相应参数(权重和偏置)
Args
----
layer : Layer_Dense
需要更新参数的层实例, 该层必须包含dweights和dbiases属性(梯度)
"""
# 如果该层没有weight_cache属性(没有历史信息, 说明是首次更新), 则初始化动量和缓存数组(与参数形状一致, 因为动量公式中每一轮迭代中的动量本质是历史梯度的一个加权平均, 所以形状要和梯度一致, 而参数的梯度形状和参数本身一致)
# 首次更新某层时,没有历史梯度数据, 所以创建与权重 / 偏置形状完全一致的全 0 数组,用于存储历史动量(weight_momentums)和历史平方梯度(weight_cache)
if not hasattr(layer, 'weight_cache'):
# layer.weights 是该层的权重参数
# layer.weight_momentums: 是该层的权重动量, 量纲是"梯度的累积"
# layer.weight_cache: 是该层的权重缓存, 量纲是"梯度平方的累积"
# 动量数组(momentums): 存储历史梯度的指数移动平均(用于动量更新)
layer.weight_momentums = np.zeros_like(layer.weights)
# np.zeros_like: 创建与layer.weights形状相同的全0数组
layer.weight_cache = np.zeros_like(layer.weights)
# 缓存数组(cache): 存储历史平方梯度的指数移动平均(用于自适应学习率)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# 1, 更新动量数组(权重与偏置) ------> ⚠️ 动量法体现
# 公式: momentum = beta_1 * previous_momentum + (1 - beta_1) * current_gradient
# mt=β1⋅mt-1+(1-β1)⋅∇Wt 当前迭代的动量=β1乘以前一迭代的动量+(1-β1)乘以当前迭代的权重梯度
# 作用: 积累历史梯度方向, 加速收敛(如沿同一方向则步长变大)
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# 2, 动量偏差修正: 初始迭代时momentum接近0, 需修正为更精确的估计 ------> 矫正加权和为1
# 公式: corrected_momentum = momentum / (1 - beta_1^(iterations + 1))
# 原因: beta1接近1, 迭代初期1 = beta1^t 较小, 修正后momentum更接近真实值
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# 3, 更新缓存数组(权重与偏置) ------> ⚠️ 自适应学习率体现(也就是RMSProp)
# 公式: cache = beta_2 * previous_cache + (1 - beta_2) * current_gradient^2
# 作用: 记录梯度平方的历史, 用于自适应调整学习率(梯度大则步长小, 反之则步长大)
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# 4, 缓存偏差修正: 同动量修正, 解决初始迭代时cache接近0的问题 ------> 矫正加权和为1 不能
# 公式: corrected_cache = cache / (1 - beta_2^(iterations + 1))
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# 5, 最终参数更新: 结合动量修正和自适应学习率
# 公式: 参数 = 参数 - 学习率*修正动量/(sqrt(修正缓存) + 小常数)
# 修正动量: 提供梯度的方向和累计效应(解决SGD震荡问题)
# 修正缓存: 调整学习率以适应不同参数的梯度规模(自适应调整每个参数的学习率, 梯度大则步长小, 避免震荡)
# 小常数: 防止除0错误, 保持数值稳定
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
def post_update_params(self):
# 迭代次数更新: 每次参数更新后迭代次数+1, 用于下一次衰减和偏差修正
self.iterations += 1
# =============================================================================
# 第二部分:通用深度网络封装 (UniversalDeepModel)
# =============================================================================
class UniversalDeepModel:
"""
Description
-----------
这是一个通用的、支持任意深度的全连接神经网络封装类; 它自动管理层的创建、前向传播、反向传播和参数更新.
本质是组装工具类, 根据后续用户配置动态搭建网络(隐藏层数量/神经元数, 输入输出维度), 并自动协调"前向传播-损失计算-反向传播-参数更新"的流程.
Notes
-----
- 1, 封装目的是为了降低使用复杂度, 用户只需指定网络结构和训练参数(数据和网络结构), 无需手动管理每一层和训练细节(也就是无需关注梯度计算/层间维度匹配等细节)
"""
def __init__(self, input_dim, hidden_layer_sizes, output_dim, learning_rate=0.001, decay=0.):
"""
Description
-----------
初始化模型架构, 动态创建隐藏层和输出层, 并设置优化器和损失函数.
只是设计网络结构, 并未进行训练, 也就是层的初始化和连接.
Args
----
input_dim (int): 输入数据的特征数量 (例如 2, 784), 主要是每一层的输入维度, 可以视为上一层的输出维度/神经元数量, 如 28x28 图像展平后为 784
hidden_layer_sizes (list of int): 一个列表,定义隐藏层的结构
例如 [64] 表示 1 个隐藏层,有 64 个神经元
例如 [128, 64] 表示 2 个隐藏层,第一层 128, 第二层 64
output_dim (int): 输出类别的数量, 例如 10 表示有 10 个类别 (0-9)
learning_rate (float): 初始学习率, 控制参数更新步长, 默认0.001
decay (float): 学习率衰减率, 防止训练后期震荡, 默认0.0(不衰减)
"""
self.layers = [] # 用于存储所有的网络层 (Dense 和 ReLU), 仅存隐藏层, 输出层单独处理, 因输出层激活函数与隐藏层不同
self.optimizer = Optimizer_Adam(learning_rate=learning_rate, decay=decay)
# --- 1. 动态构建隐藏层 ---
# current_input_dim 记录当前层的输入维度,初始为数据的输入维度
current_input_dim = input_dim
for i, n_neurons in enumerate(hidden_layer_sizes):
# 创建全连接层:输入维度current_input_dim -> 当前隐藏层神经元数n_neurons
# 隐藏层的固定结构:全连接层(线性变换)+ ReLU 层(非线性激活)
# 示例, 若hidden_layer_sizes=[64,32], 则self.layers会依次添加: Dense(input_dim->64)->ReLU->Dense(64->32)->ReLU
dense_layer = Layer_Dense(current_input_dim, n_neurons)
self.layers.append(dense_layer)
# 创建激活函数层:每个全连接层后通常接一个 ReLU, 引入非线性
activation_layer = Activation_ReLU()
self.layers.append(activation_layer)
# 更新下一层的输入维度为当前层的神经元数
current_input_dim = n_neurons
print(f"构建层 {i+1}: Dense({dense_layer.weights.shape[0]}->{n_neurons}) + ReLU")
# --- 2. 构建输出层 ---
# 最后一层全连接:最后一个隐藏层神经元数 -> 输出类别数
# 注意:最后一层通常不接 ReLU,而是接 Softmax (包含在 loss_activation 中)
# 单独存储输出层全连接层(因后续反向传播需优先处理输出层梯度)
self.final_dense = Layer_Dense(current_input_dim, output_dim)
print(f"构建输出层: Dense({current_input_dim}->{output_dim}) + Softmax")
# --- 3. 定义损失函数和输出激活 ---
# 使用 Softmax + CrossEntropy 的组合类
# 输出层激活+损失:Softmax(概率化)+ 交叉熵(损失计算)组合类
self.loss_activation = Activation_Softmax_Loss_CategoricalCrossentropy()
def forward(self, X):
"""
Description
-----------
前向传播:数据从输入流向输出, 只是计算输出, 不进行训练.
前向传播是 "数据流转阶段":输入数据从隐藏层逐层传递,最终经过输出层全连接层,得到线性输出(Logits)(Softmax 在损失计算时才执行);
层间传递:每个层的 forward 方法会更新自身的 self.output, 并作为下一层的输入, 无需用户手动处理维度匹配(底层 Layer_Dense 已保证维度正确)
Args
----
X (np.ndarray): 输入数据, 形状为(样本数, 特征数)
"""
# 1. 数据先流经所有隐藏层
current_output = X # 初始输入为原始数据
for layer in self.layers:
layer.forward(current_output) # 调用层的前向传播(Dense算线性输出,ReLU做激活)
current_output = layer.output # 将当前层的输出作为下一层的输入
# 2. 流经最后一个全连接层
self.final_dense.forward(current_output)
# 3. 返回最终层的输出 (Logits),注意此时还没过 Softmax
# Softmax 激活被封装在 loss_activation 中,会在计算损失时自动执行(避免重复计算)
return self.final_dense.output
def train(self, X, y, epochs=1000, print_every=100):
"""
Description
-----------
训练循环, 是模型的 "迭代优化阶段",整合了 "前向传播→损失计算→梯度反向传播→参数更新" 的全流程,是训练模型的入口.
Args
----
X (np.ndarray): 输入数据, 形状为(样本数, 特征数)
y (np.ndarray): 真实标签, 可为类别索引或独热编码, 形状为(样本数,)或(样本数, 类别数) (独热编码)
epochs (int): 训练轮数, 控制训练的迭代次数, 默认1000
print_every (int): 每多少轮打印一次训练状态, 默认100
"""
for epoch in range(epochs):
# ====================
# A. 前向传播 (Forward)
# ====================
# 1. 计算网络主体输出, 线性输出(Logits)
final_outputs = self.forward(X)
# 2. 计算损失 (同时做 Softmax)
# self.loss_activation.forward 接收Logits,先做Softmax得到概率,再算交叉熵损失
# forward 返回的是 loss 值
loss = self.loss_activation.forward(final_outputs, y)
# ====================
# B. 打印状态 (Logging)
# ====================
if not epoch % print_every:
# 1. 计算预测类别(从概率分布取最大值索引)
predictions = np.argmax(self.loss_activation.output, axis=1)
# 2. 处理标签(若为独热编码,转成类别索引)
if len(y.shape) == 2:
y_labels = np.argmax(y, axis=1)
else:
y_labels = y
# 3. 计算准确率(预测正确的样本数 / 总样本数)
accuracy = np.mean(predictions == y_labels)
# 4. 打印当前轮数, 准确率, 损失, 学习率, 梯度范数⚠️
# 如果可以还想打印一下梯度的范数
print(f'Epoch: {epoch}, ' +
f'Acc: {accuracy:.3f}, ' +
f'Loss: {loss:.3f}, ' +
f'LR: {self.optimizer.current_learning_rate:.6f}, '+
f'Grad Norm: {np.mean([np.linalg.norm(layer.dweights) for layer in self.layers if hasattr(layer, "dweights")]):.3f}')
# ====================
# C. 反向传播 (Backward)
# 反向传播是 "梯度回流阶段",核心是根据损失计算所有参数(权重、偏置)的梯度,遵循 "从输出层→隐藏层→输入层" 的顺序(梯度链式法则)
# ====================
# 1. 从 Loss 开始反向传播
# 1. 从损失层开始反向传播(计算对Logits的梯度)
# self.loss_activation.backward 直接返回损失对输出层全连接层输出(Logits)的梯度
self.loss_activation.backward(self.loss_activation.output, y)
# 2. 反向传播经过输出层
# 输入是 loss 层的梯度 (dinputs)
# 2. 输出层全连接层反向传播(计算对输出层权重/偏置的梯度,及对隐藏层输出的梯度)
self.final_dense.backward(self.loss_activation.dinputs)
# 3. 反向传播经过所有隐藏层 (需要倒序遍历!因为梯度从后往前传)
# 这里的梯度链是:上一层的 dinputs -> 当前层的 backward
# 初始梯度:输出层对隐藏层输出的梯度
back_gradient = self.final_dense.dinputs
for layer in reversed(self.layers):
layer.backward(back_gradient) # 调用层的反向传播(计算当前层梯度)
back_gradient = layer.dinputs # 更新梯度:当前层对前一层输入的梯度 → 传给前一层
# ====================
# D. 参数更新 (Optimize)
# ====================
# 1. 预更新:处理学习率衰减(若开启)
self.optimizer.pre_update_params()
# 2. 更新隐藏层的参数(仅全连接层有参数,ReLU无参数)
for layer in self.layers:
# 只有 Layer_Dense 有参数(weights/biases),ReLU 没有
if hasattr(layer, 'weights'):
self.optimizer.update_params(layer)
# 3. 更新输出层的参数
self.optimizer.update_params(self.final_dense)
# 4. 后更新:迭代次数+1(用于下一轮衰减计算和Adam的偏差修正)
self.optimizer.post_update_params()
def predict(self, X):
"""
Description
-----------
使用训练好的模型进行预测, 返回类别概率分布.
训练完成后,通过 predict 方法对新数据进行预测,输出类别概率分布(方便用户判断预测置信度)
预测函数:输入数据,输出概率分布
推理流程:新数据→前向传播(Logits)→Softmax(概率)
Args
----
X : np.ndarray
输入数据, 形状为(样本数, 特征数)
Notes
-----
- 1, 输出解读:例如输出 [[0.05, 0.9, 0.05]] 表示样本属于第 2 类的概率为 90%,可通过 np.argmax(probs, axis=1) 得到最终预测类别
"""
# 1. 前向传播得到Logits(线性输出)
logits = self.forward(X)
# 2. 对Logits执行Softmax,转为概率分布
self.loss_activation.activation.forward(logits)
# 3. 返回概率分布(形状:(样本数, 类别数))
return self.loss_activation.activation.output
# =============================================================================
# 第三部分:【用户配置区】 (万金油模板接口)
# =============================================================================
# --- 1. 数据准备 (Data Preparation) ---
# 这里是唯一需要你根据实际任务修改数据加载逻辑的地方
# 示例:生成 300 个样本,2 个特征,3 分类
print("正在生成数据...")
N_SAMPLES = 300
INPUT_FEATURES = 2
NUM_CLASSES = 3
X_data = np.random.randn(N_SAMPLES, INPUT_FEATURES) # 你的输入数据, 随机生成标准正态分布数据, 形状 (300, 2)
y_data = np.random.randint(0, NUM_CLASSES, size=(N_SAMPLES,)) # 你的标签, 随机生成 0,1,2 三类标签, 形状 (300,)
# --- 2. 模型配置 (Model Configuration) ---
# 只要修改这里,就能改变网络的深度和宽度
# 场景 A: 简单网络 -> hidden_layers = [64]
# 场景 B: 深层网络 -> hidden_layers = [128, 128, 64]
MY_HIDDEN_LAYERS = [64, 64] # 2个隐藏层,每层64个神经元
model = UniversalDeepModel(
input_dim=INPUT_FEATURES, # 自动适配输入数据
hidden_layer_sizes=MY_HIDDEN_LAYERS, # 在这里定义你有多少层,每层多大
output_dim=NUM_CLASSES, # 自动适配输出类别
learning_rate=0.05, # 学习率
decay=1e-4 # 学习率衰减 (防止后期震荡)
)
# --- 3. 训练 (Training) ---
print("\n开始训练...")
model.train(
X_data,
y_data,
epochs=2000, # 训练轮数
print_every=10 # 每多少轮打印一次
)
# --- 4. 验证/使用 (Inference) ---
print("\n模型使用示例:")
# 假设来了一条新数据
new_sample = np.array([[0.5, -1.2]]) # 新样本, 形状 (1, 2)
probs = model.predict(new_sample) # 预测类别概率分布, 形状 (1, 3)
pred_class = np.argmax(probs, axis=1) # 预测类别索引
print(f"输入: {new_sample}")
print(f"各类别概率: {probs}")
print(f"预测类别: {pred_class}")可视化略,要实现可以通过matplotlib实现,打印一些model训练过程中的参数、日志之类。
梯度范数之所以打印,是我在这里特别加进去的,是为了能够判断我们在model loss一直降不下去的时候,判断到底是不是卡在了局部极值点还是saddle point(梯度为0的地方)。
下面是日志输出:
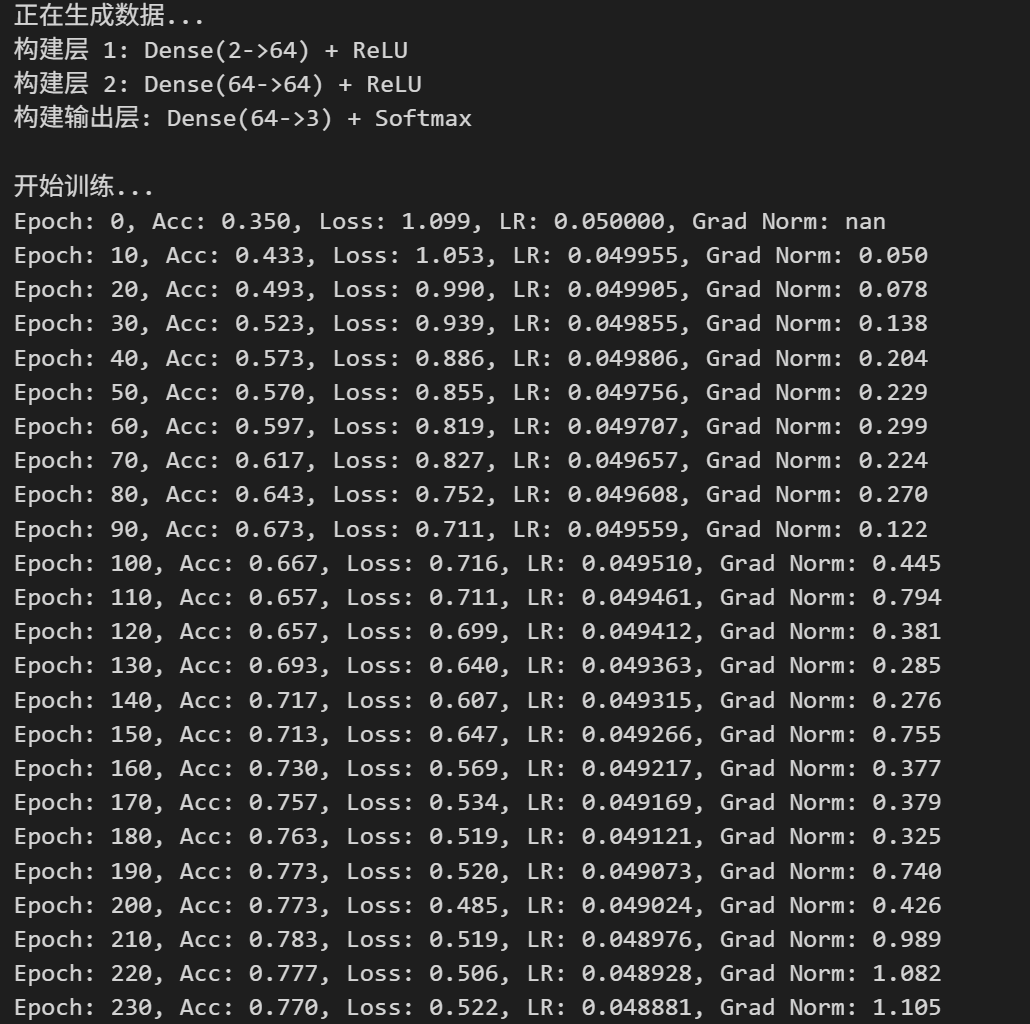
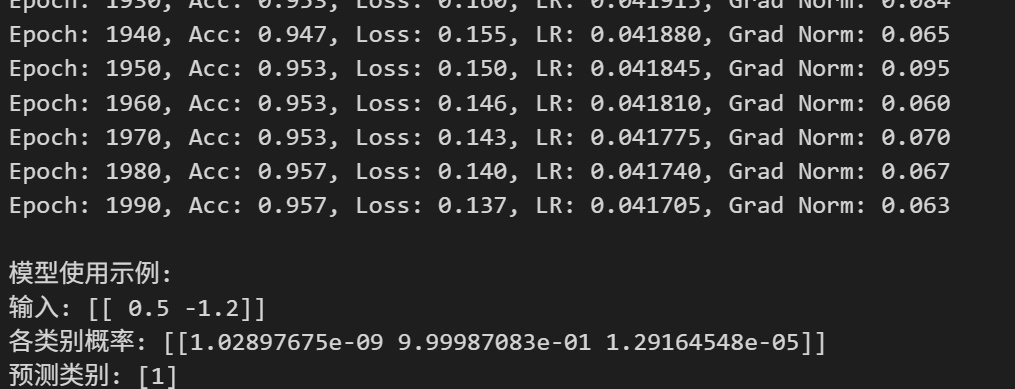
python
正在生成数据...
构建层 1: Dense(2->64) + ReLU
构建层 2: Dense(64->64) + ReLU
构建输出层: Dense(64->3) + Softmax
开始训练...
Epoch: 0, Acc: 0.350, Loss: 1.099, LR: 0.050000, Grad Norm: nan
Epoch: 10, Acc: 0.433, Loss: 1.053, LR: 0.049955, Grad Norm: 0.050
Epoch: 20, Acc: 0.493, Loss: 0.990, LR: 0.049905, Grad Norm: 0.078
Epoch: 30, Acc: 0.523, Loss: 0.939, LR: 0.049855, Grad Norm: 0.138
Epoch: 40, Acc: 0.573, Loss: 0.886, LR: 0.049806, Grad Norm: 0.204
Epoch: 50, Acc: 0.570, Loss: 0.855, LR: 0.049756, Grad Norm: 0.229
Epoch: 60, Acc: 0.597, Loss: 0.819, LR: 0.049707, Grad Norm: 0.299
Epoch: 70, Acc: 0.617, Loss: 0.827, LR: 0.049657, Grad Norm: 0.224
Epoch: 80, Acc: 0.643, Loss: 0.752, LR: 0.049608, Grad Norm: 0.270
Epoch: 90, Acc: 0.673, Loss: 0.711, LR: 0.049559, Grad Norm: 0.122
Epoch: 100, Acc: 0.667, Loss: 0.716, LR: 0.049510, Grad Norm: 0.445
Epoch: 110, Acc: 0.657, Loss: 0.711, LR: 0.049461, Grad Norm: 0.794
Epoch: 120, Acc: 0.657, Loss: 0.699, LR: 0.049412, Grad Norm: 0.381
Epoch: 130, Acc: 0.693, Loss: 0.640, LR: 0.049363, Grad Norm: 0.285
Epoch: 140, Acc: 0.717, Loss: 0.607, LR: 0.049315, Grad Norm: 0.276
Epoch: 150, Acc: 0.713, Loss: 0.647, LR: 0.049266, Grad Norm: 0.755
Epoch: 160, Acc: 0.730, Loss: 0.569, LR: 0.049217, Grad Norm: 0.377
Epoch: 170, Acc: 0.757, Loss: 0.534, LR: 0.049169, Grad Norm: 0.379
Epoch: 180, Acc: 0.763, Loss: 0.519, LR: 0.049121, Grad Norm: 0.325
Epoch: 190, Acc: 0.773, Loss: 0.520, LR: 0.049073, Grad Norm: 0.740
Epoch: 200, Acc: 0.773, Loss: 0.485, LR: 0.049024, Grad Norm: 0.426
Epoch: 210, Acc: 0.783, Loss: 0.519, LR: 0.048976, Grad Norm: 0.989
Epoch: 220, Acc: 0.777, Loss: 0.506, LR: 0.048928, Grad Norm: 1.082
Epoch: 230, Acc: 0.770, Loss: 0.522, LR: 0.048881, Grad Norm: 1.105
Epoch: 240, Acc: 0.780, Loss: 0.484, LR: 0.048833, Grad Norm: 0.712
Epoch: 250, Acc: 0.803, Loss: 0.469, LR: 0.048785, Grad Norm: 1.029
Epoch: 260, Acc: 0.770, Loss: 0.544, LR: 0.048738, Grad Norm: 1.021
Epoch: 270, Acc: 0.790, Loss: 0.472, LR: 0.048690, Grad Norm: 0.592
Epoch: 280, Acc: 0.807, Loss: 0.427, LR: 0.048643, Grad Norm: 0.671
Epoch: 290, Acc: 0.823, Loss: 0.411, LR: 0.048596, Grad Norm: 0.554
Epoch: 300, Acc: 0.837, Loss: 0.376, LR: 0.048548, Grad Norm: 0.402
Epoch: 310, Acc: 0.837, Loss: 0.359, LR: 0.048501, Grad Norm: 0.252
Epoch: 320, Acc: 0.857, Loss: 0.345, LR: 0.048454, Grad Norm: 0.153
Epoch: 330, Acc: 0.860, Loss: 0.335, LR: 0.048407, Grad Norm: 0.208
Epoch: 340, Acc: 0.850, Loss: 0.345, LR: 0.048361, Grad Norm: 0.537
Epoch: 350, Acc: 0.757, Loss: 0.599, LR: 0.048314, Grad Norm: 1.326
Epoch: 360, Acc: 0.810, Loss: 0.501, LR: 0.048267, Grad Norm: 1.053
Epoch: 370, Acc: 0.790, Loss: 0.501, LR: 0.048221, Grad Norm: 1.140
Epoch: 380, Acc: 0.813, Loss: 0.404, LR: 0.048174, Grad Norm: 1.263
Epoch: 390, Acc: 0.840, Loss: 0.351, LR: 0.048128, Grad Norm: 0.627
Epoch: 400, Acc: 0.857, Loss: 0.329, LR: 0.048082, Grad Norm: 0.429
Epoch: 410, Acc: 0.863, Loss: 0.310, LR: 0.048035, Grad Norm: 0.260
Epoch: 420, Acc: 0.863, Loss: 0.300, LR: 0.047989, Grad Norm: 0.208
Epoch: 430, Acc: 0.870, Loss: 0.290, LR: 0.047943, Grad Norm: 0.182
Epoch: 440, Acc: 0.880, Loss: 0.281, LR: 0.047897, Grad Norm: 0.184
Epoch: 450, Acc: 0.873, Loss: 0.287, LR: 0.047851, Grad Norm: 0.751
Epoch: 460, Acc: 0.880, Loss: 0.303, LR: 0.047806, Grad Norm: 0.725
Epoch: 470, Acc: 0.897, Loss: 0.274, LR: 0.047760, Grad Norm: 0.358
Epoch: 480, Acc: 0.893, Loss: 0.270, LR: 0.047714, Grad Norm: 0.491
Epoch: 490, Acc: 0.897, Loss: 0.258, LR: 0.047669, Grad Norm: 0.390
Epoch: 500, Acc: 0.887, Loss: 0.260, LR: 0.047624, Grad Norm: 0.443
Epoch: 510, Acc: 0.873, Loss: 0.255, LR: 0.047578, Grad Norm: 0.390
Epoch: 520, Acc: 0.907, Loss: 0.245, LR: 0.047533, Grad Norm: 0.231
Epoch: 530, Acc: 0.877, Loss: 0.276, LR: 0.047488, Grad Norm: 0.782
Epoch: 540, Acc: 0.807, Loss: 0.638, LR: 0.047443, Grad Norm: 3.128
Epoch: 550, Acc: 0.693, Loss: 1.010, LR: 0.047398, Grad Norm: 3.243
Epoch: 560, Acc: 0.707, Loss: 0.807, LR: 0.047353, Grad Norm: 1.730
Epoch: 570, Acc: 0.747, Loss: 0.545, LR: 0.047308, Grad Norm: 1.159
Epoch: 580, Acc: 0.790, Loss: 0.415, LR: 0.047263, Grad Norm: 1.064
Epoch: 590, Acc: 0.867, Loss: 0.329, LR: 0.047219, Grad Norm: 0.388
Epoch: 600, Acc: 0.893, Loss: 0.291, LR: 0.047174, Grad Norm: 0.271
Epoch: 610, Acc: 0.900, Loss: 0.275, LR: 0.047130, Grad Norm: 0.197
Epoch: 620, Acc: 0.907, Loss: 0.264, LR: 0.047085, Grad Norm: 0.198
Epoch: 630, Acc: 0.910, Loss: 0.255, LR: 0.047041, Grad Norm: 0.221
Epoch: 640, Acc: 0.920, Loss: 0.249, LR: 0.046997, Grad Norm: 0.204
Epoch: 650, Acc: 0.913, Loss: 0.246, LR: 0.046953, Grad Norm: 0.163
Epoch: 660, Acc: 0.913, Loss: 0.239, LR: 0.046909, Grad Norm: 0.178
Epoch: 670, Acc: 0.913, Loss: 0.233, LR: 0.046865, Grad Norm: 0.275
Epoch: 680, Acc: 0.930, Loss: 0.232, LR: 0.046821, Grad Norm: 0.178
Epoch: 690, Acc: 0.923, Loss: 0.223, LR: 0.046777, Grad Norm: 0.270
Epoch: 700, Acc: 0.927, Loss: 0.218, LR: 0.046733, Grad Norm: 0.184
Epoch: 710, Acc: 0.930, Loss: 0.214, LR: 0.046690, Grad Norm: 0.154
Epoch: 720, Acc: 0.930, Loss: 0.209, LR: 0.046646, Grad Norm: 0.204
Epoch: 730, Acc: 0.933, Loss: 0.207, LR: 0.046603, Grad Norm: 0.211
Epoch: 740, Acc: 0.933, Loss: 0.203, LR: 0.046559, Grad Norm: 0.206
Epoch: 750, Acc: 0.937, Loss: 0.201, LR: 0.046516, Grad Norm: 0.314
Epoch: 760, Acc: 0.933, Loss: 0.196, LR: 0.046473, Grad Norm: 0.262
Epoch: 770, Acc: 0.937, Loss: 0.193, LR: 0.046430, Grad Norm: 0.364
Epoch: 780, Acc: 0.923, Loss: 0.202, LR: 0.046386, Grad Norm: 0.672
Epoch: 790, Acc: 0.940, Loss: 0.188, LR: 0.046343, Grad Norm: 0.448
Epoch: 800, Acc: 0.920, Loss: 0.220, LR: 0.046301, Grad Norm: 0.833
Epoch: 810, Acc: 0.837, Loss: 0.546, LR: 0.046258, Grad Norm: 3.338
Epoch: 820, Acc: 0.807, Loss: 0.578, LR: 0.046215, Grad Norm: 1.729
Epoch: 830, Acc: 0.853, Loss: 0.390, LR: 0.046172, Grad Norm: 1.985
Epoch: 840, Acc: 0.853, Loss: 0.335, LR: 0.046130, Grad Norm: 1.138
Epoch: 850, Acc: 0.893, Loss: 0.278, LR: 0.046087, Grad Norm: 1.414
Epoch: 860, Acc: 0.910, Loss: 0.245, LR: 0.046045, Grad Norm: 1.492
Epoch: 870, Acc: 0.903, Loss: 0.239, LR: 0.046002, Grad Norm: 0.786
Epoch: 880, Acc: 0.933, Loss: 0.210, LR: 0.045960, Grad Norm: 0.529
Epoch: 890, Acc: 0.933, Loss: 0.201, LR: 0.045918, Grad Norm: 0.263
Epoch: 900, Acc: 0.937, Loss: 0.195, LR: 0.045876, Grad Norm: 0.179
Epoch: 910, Acc: 0.940, Loss: 0.190, LR: 0.045834, Grad Norm: 0.111
Epoch: 920, Acc: 0.937, Loss: 0.187, LR: 0.045792, Grad Norm: 0.118
Epoch: 930, Acc: 0.937, Loss: 0.183, LR: 0.045750, Grad Norm: 0.103
Epoch: 940, Acc: 0.947, Loss: 0.177, LR: 0.045708, Grad Norm: 0.092
Epoch: 950, Acc: 0.947, Loss: 0.173, LR: 0.045666, Grad Norm: 0.110
Epoch: 960, Acc: 0.950, Loss: 0.170, LR: 0.045625, Grad Norm: 0.087
Epoch: 970, Acc: 0.943, Loss: 0.167, LR: 0.045583, Grad Norm: 0.153
Epoch: 980, Acc: 0.950, Loss: 0.165, LR: 0.045541, Grad Norm: 0.130
Epoch: 990, Acc: 0.947, Loss: 0.163, LR: 0.045500, Grad Norm: 0.102
Epoch: 1000, Acc: 0.943, Loss: 0.160, LR: 0.045459, Grad Norm: 0.112
Epoch: 1010, Acc: 0.940, Loss: 0.158, LR: 0.045417, Grad Norm: 0.114
Epoch: 1020, Acc: 0.947, Loss: 0.155, LR: 0.045376, Grad Norm: 0.097
Epoch: 1030, Acc: 0.950, Loss: 0.154, LR: 0.045335, Grad Norm: 0.157
Epoch: 1040, Acc: 0.953, Loss: 0.152, LR: 0.045294, Grad Norm: 0.088
Epoch: 1050, Acc: 0.953, Loss: 0.150, LR: 0.045253, Grad Norm: 0.100
Epoch: 1060, Acc: 0.947, Loss: 0.149, LR: 0.045212, Grad Norm: 0.172
Epoch: 1070, Acc: 0.957, Loss: 0.146, LR: 0.045171, Grad Norm: 0.119
Epoch: 1080, Acc: 0.957, Loss: 0.145, LR: 0.045130, Grad Norm: 0.135
Epoch: 1090, Acc: 0.960, Loss: 0.149, LR: 0.045090, Grad Norm: 0.882
Epoch: 1100, Acc: 0.940, Loss: 0.183, LR: 0.045049, Grad Norm: 1.262
Epoch: 1110, Acc: 0.903, Loss: 0.246, LR: 0.045009, Grad Norm: 1.801
Epoch: 1120, Acc: 0.823, Loss: 0.594, LR: 0.044968, Grad Norm: 2.595
Epoch: 1130, Acc: 0.750, Loss: 0.963, LR: 0.044928, Grad Norm: 3.524
Epoch: 1140, Acc: 0.773, Loss: 0.588, LR: 0.044887, Grad Norm: 1.808
Epoch: 1150, Acc: 0.840, Loss: 0.538, LR: 0.044847, Grad Norm: 2.559
Epoch: 1160, Acc: 0.863, Loss: 0.346, LR: 0.044807, Grad Norm: 1.401
Epoch: 1170, Acc: 0.893, Loss: 0.219, LR: 0.044767, Grad Norm: 0.741
Epoch: 1180, Acc: 0.937, Loss: 0.193, LR: 0.044727, Grad Norm: 0.469
Epoch: 1190, Acc: 0.953, Loss: 0.173, LR: 0.044687, Grad Norm: 0.307
Epoch: 1200, Acc: 0.953, Loss: 0.163, LR: 0.044647, Grad Norm: 0.158
Epoch: 1210, Acc: 0.960, Loss: 0.158, LR: 0.044607, Grad Norm: 0.119
Epoch: 1220, Acc: 0.960, Loss: 0.155, LR: 0.044567, Grad Norm: 0.132
Epoch: 1230, Acc: 0.963, Loss: 0.151, LR: 0.044528, Grad Norm: 0.097
Epoch: 1240, Acc: 0.960, Loss: 0.148, LR: 0.044488, Grad Norm: 0.188
Epoch: 1250, Acc: 0.963, Loss: 0.146, LR: 0.044448, Grad Norm: 0.191
Epoch: 1260, Acc: 0.957, Loss: 0.145, LR: 0.044409, Grad Norm: 0.114
Epoch: 1270, Acc: 0.960, Loss: 0.141, LR: 0.044370, Grad Norm: 0.133
Epoch: 1280, Acc: 0.960, Loss: 0.139, LR: 0.044330, Grad Norm: 0.153
Epoch: 1290, Acc: 0.963, Loss: 0.137, LR: 0.044291, Grad Norm: 0.121
Epoch: 1300, Acc: 0.960, Loss: 0.135, LR: 0.044252, Grad Norm: 0.090
Epoch: 1310, Acc: 0.960, Loss: 0.134, LR: 0.044213, Grad Norm: 0.097
Epoch: 1320, Acc: 0.963, Loss: 0.133, LR: 0.044174, Grad Norm: 0.119
Epoch: 1330, Acc: 0.963, Loss: 0.131, LR: 0.044135, Grad Norm: 0.123
Epoch: 1340, Acc: 0.973, Loss: 0.129, LR: 0.044096, Grad Norm: 0.106
Epoch: 1350, Acc: 0.967, Loss: 0.127, LR: 0.044057, Grad Norm: 0.091
Epoch: 1360, Acc: 0.973, Loss: 0.126, LR: 0.044018, Grad Norm: 0.113
Epoch: 1370, Acc: 0.967, Loss: 0.124, LR: 0.043979, Grad Norm: 0.100
Epoch: 1380, Acc: 0.967, Loss: 0.123, LR: 0.043941, Grad Norm: 0.126
Epoch: 1390, Acc: 0.967, Loss: 0.121, LR: 0.043902, Grad Norm: 0.090
Epoch: 1400, Acc: 0.967, Loss: 0.121, LR: 0.043863, Grad Norm: 0.107
Epoch: 1410, Acc: 0.970, Loss: 0.119, LR: 0.043825, Grad Norm: 0.137
Epoch: 1420, Acc: 0.970, Loss: 0.118, LR: 0.043787, Grad Norm: 0.092
Epoch: 1430, Acc: 0.967, Loss: 0.117, LR: 0.043748, Grad Norm: 0.093
Epoch: 1440, Acc: 0.970, Loss: 0.115, LR: 0.043710, Grad Norm: 0.116
Epoch: 1450, Acc: 0.967, Loss: 0.114, LR: 0.043672, Grad Norm: 0.083
Epoch: 1460, Acc: 0.970, Loss: 0.113, LR: 0.043634, Grad Norm: 0.077
Epoch: 1470, Acc: 0.970, Loss: 0.111, LR: 0.043596, Grad Norm: 0.086
Epoch: 1480, Acc: 0.970, Loss: 0.110, LR: 0.043558, Grad Norm: 0.073
Epoch: 1490, Acc: 0.970, Loss: 0.110, LR: 0.043520, Grad Norm: 0.122
Epoch: 1500, Acc: 0.973, Loss: 0.109, LR: 0.043482, Grad Norm: 0.141
Epoch: 1510, Acc: 0.973, Loss: 0.107, LR: 0.043444, Grad Norm: 0.086
Epoch: 1520, Acc: 0.973, Loss: 0.106, LR: 0.043407, Grad Norm: 0.104
Epoch: 1530, Acc: 0.970, Loss: 0.105, LR: 0.043369, Grad Norm: 0.111
Epoch: 1540, Acc: 0.967, Loss: 0.105, LR: 0.043331, Grad Norm: 0.097
Epoch: 1550, Acc: 0.970, Loss: 0.105, LR: 0.043294, Grad Norm: 0.176
Epoch: 1560, Acc: 0.973, Loss: 0.104, LR: 0.043256, Grad Norm: 0.101
Epoch: 1570, Acc: 0.970, Loss: 0.102, LR: 0.043219, Grad Norm: 0.138
Epoch: 1580, Acc: 0.967, Loss: 0.103, LR: 0.043182, Grad Norm: 0.299
Epoch: 1590, Acc: 0.963, Loss: 0.101, LR: 0.043144, Grad Norm: 0.275
Epoch: 1600, Acc: 0.967, Loss: 0.100, LR: 0.043107, Grad Norm: 0.132
Epoch: 1610, Acc: 0.967, Loss: 0.106, LR: 0.043070, Grad Norm: 0.519
Epoch: 1620, Acc: 0.967, Loss: 0.101, LR: 0.043033, Grad Norm: 0.177
Epoch: 1630, Acc: 0.967, Loss: 0.097, LR: 0.042996, Grad Norm: 0.184
Epoch: 1640, Acc: 0.970, Loss: 0.098, LR: 0.042959, Grad Norm: 0.170
Epoch: 1650, Acc: 0.973, Loss: 0.096, LR: 0.042922, Grad Norm: 0.148
Epoch: 1660, Acc: 0.970, Loss: 0.095, LR: 0.042885, Grad Norm: 0.118
Epoch: 1670, Acc: 0.970, Loss: 0.093, LR: 0.042849, Grad Norm: 0.067
Epoch: 1680, Acc: 0.973, Loss: 0.093, LR: 0.042812, Grad Norm: 0.143
Epoch: 1690, Acc: 0.970, Loss: 0.092, LR: 0.042775, Grad Norm: 0.096
Epoch: 1700, Acc: 0.970, Loss: 0.091, LR: 0.042739, Grad Norm: 0.087
Epoch: 1710, Acc: 0.967, Loss: 0.090, LR: 0.042702, Grad Norm: 0.110
Epoch: 1720, Acc: 0.973, Loss: 0.090, LR: 0.042666, Grad Norm: 0.065
Epoch: 1730, Acc: 0.973, Loss: 0.089, LR: 0.042629, Grad Norm: 0.075
Epoch: 1740, Acc: 0.970, Loss: 0.089, LR: 0.042593, Grad Norm: 0.139
Epoch: 1750, Acc: 0.973, Loss: 0.088, LR: 0.042557, Grad Norm: 0.201
Epoch: 1760, Acc: 0.973, Loss: 0.087, LR: 0.042521, Grad Norm: 0.112
Epoch: 1770, Acc: 0.973, Loss: 0.090, LR: 0.042484, Grad Norm: 0.425
Epoch: 1780, Acc: 0.970, Loss: 0.086, LR: 0.042448, Grad Norm: 0.282
Epoch: 1790, Acc: 0.973, Loss: 0.085, LR: 0.042412, Grad Norm: 0.126
Epoch: 1800, Acc: 0.977, Loss: 0.086, LR: 0.042376, Grad Norm: 0.314
Epoch: 1810, Acc: 0.970, Loss: 0.086, LR: 0.042341, Grad Norm: 0.236
Epoch: 1820, Acc: 0.747, Loss: 2.130, LR: 0.042305, Grad Norm: 6.721
Epoch: 1830, Acc: 0.657, Loss: 1.662, LR: 0.042269, Grad Norm: 6.141
Epoch: 1840, Acc: 0.740, Loss: 0.828, LR: 0.042233, Grad Norm: 2.452
Epoch: 1850, Acc: 0.700, Loss: 0.986, LR: 0.042198, Grad Norm: 3.132
Epoch: 1860, Acc: 0.820, Loss: 0.506, LR: 0.042162, Grad Norm: 2.407
Epoch: 1870, Acc: 0.840, Loss: 0.389, LR: 0.042127, Grad Norm: 1.232
Epoch: 1880, Acc: 0.887, Loss: 0.272, LR: 0.042091, Grad Norm: 0.961
Epoch: 1890, Acc: 0.920, Loss: 0.215, LR: 0.042056, Grad Norm: 0.322
Epoch: 1900, Acc: 0.937, Loss: 0.189, LR: 0.042020, Grad Norm: 0.198
Epoch: 1910, Acc: 0.947, Loss: 0.175, LR: 0.041985, Grad Norm: 0.139
Epoch: 1920, Acc: 0.950, Loss: 0.166, LR: 0.041950, Grad Norm: 0.117
Epoch: 1930, Acc: 0.953, Loss: 0.160, LR: 0.041915, Grad Norm: 0.084
Epoch: 1940, Acc: 0.947, Loss: 0.155, LR: 0.041880, Grad Norm: 0.065
Epoch: 1950, Acc: 0.953, Loss: 0.150, LR: 0.041845, Grad Norm: 0.095
Epoch: 1960, Acc: 0.953, Loss: 0.146, LR: 0.041810, Grad Norm: 0.060
Epoch: 1970, Acc: 0.953, Loss: 0.143, LR: 0.041775, Grad Norm: 0.070
Epoch: 1980, Acc: 0.957, Loss: 0.140, LR: 0.041740, Grad Norm: 0.067
Epoch: 1990, Acc: 0.957, Loss: 0.137, LR: 0.041705, Grad Norm: 0.063
模型使用示例:
输入: [[ 0.5 -1.2]]
各类别概率: [[1.02897675e-09 9.99987083e-01 1.29164548e-05]]
预测类别: [1]看看我们的运行时间:
纯CPU,0.4s
一些推导中需要注意的地方
其中一些需要注意的地方:
类别索引转换为独热编码索引,用到了np.eye,以及Numpy高级索引的广播匹配机制
python
import numpy as np
y_true = np.random.randint(0,3, size=100) # 100个样本的真实类别索引, 范围0-2
y_true_onehot = np.eye(3)[y_true] # 转换为独热编码形式
print(y_true_onehot)
还有就是softmax+交叉熵损失层的反向传播计算梯度,这一部分的代码,其中一些公式的计算细节:
该层的dinputs,实际上计算的就是整体loss损失对于Logits的梯度,

在推导前,我摸嗯先统一一下符合和变量定义
| 符号 / 变量 | 数学含义 | 代码对应对象 | 形状 |
|---|---|---|---|
Logits |
输出层全连接层的线性输出(未经过 Softmax) | Layer_Dense.output (final_dense 层) |
(样本数,类别数) → (N,C) |
y_pred |
Softmax 激活后的预测概率分布 | Activation_Softmax.output |
(N,C) |
y_true_onehot |
真实标签的独热编码 | np.eye(labels)[y_true] |
(N,C) |
L |
交叉熵损失(平均损失,对所有样本取平均) | Loss_CategoricalCrossentropy.calculate 输出 |
标量 |
∂L/∂y_pred |
损失对 Softmax 输出的梯度 | Loss_CategoricalCrossentropy.dinputs |
(N,C) |
∂y_pred/∂Logits |
Softmax 输出对 Logits 的梯度 | 需推导(Softmax 层的梯度) | (N,C,C)(样本级雅可比矩阵) |
∂L/∂Logits |
最终目标:损失对 Logits 的梯度 | Activation_Softmax_Loss_CategoricalCrossentropy.dinputs |
(N,C) |

简单来说就是
python
∂L/∂in_softmax = ∂L/∂out_softmax * ∂out_softmax/∂in_softmax
# 注意这里只是矩阵公式推导, *是矩阵乘法, 不是代码实现中的哈达玛乘积
# 公式推导注意和numpy代码实现分开先推导

其实就是∂L/∂out_softmax,但是这一步其实在前面交叉熵损失层的backward反向传播梯度中已经推导过了;
因为out_softmax实际上就是交叉熵损失层的input,
所以后者backward中推导的dinputs,实际上就是∂L/∂out_softmax
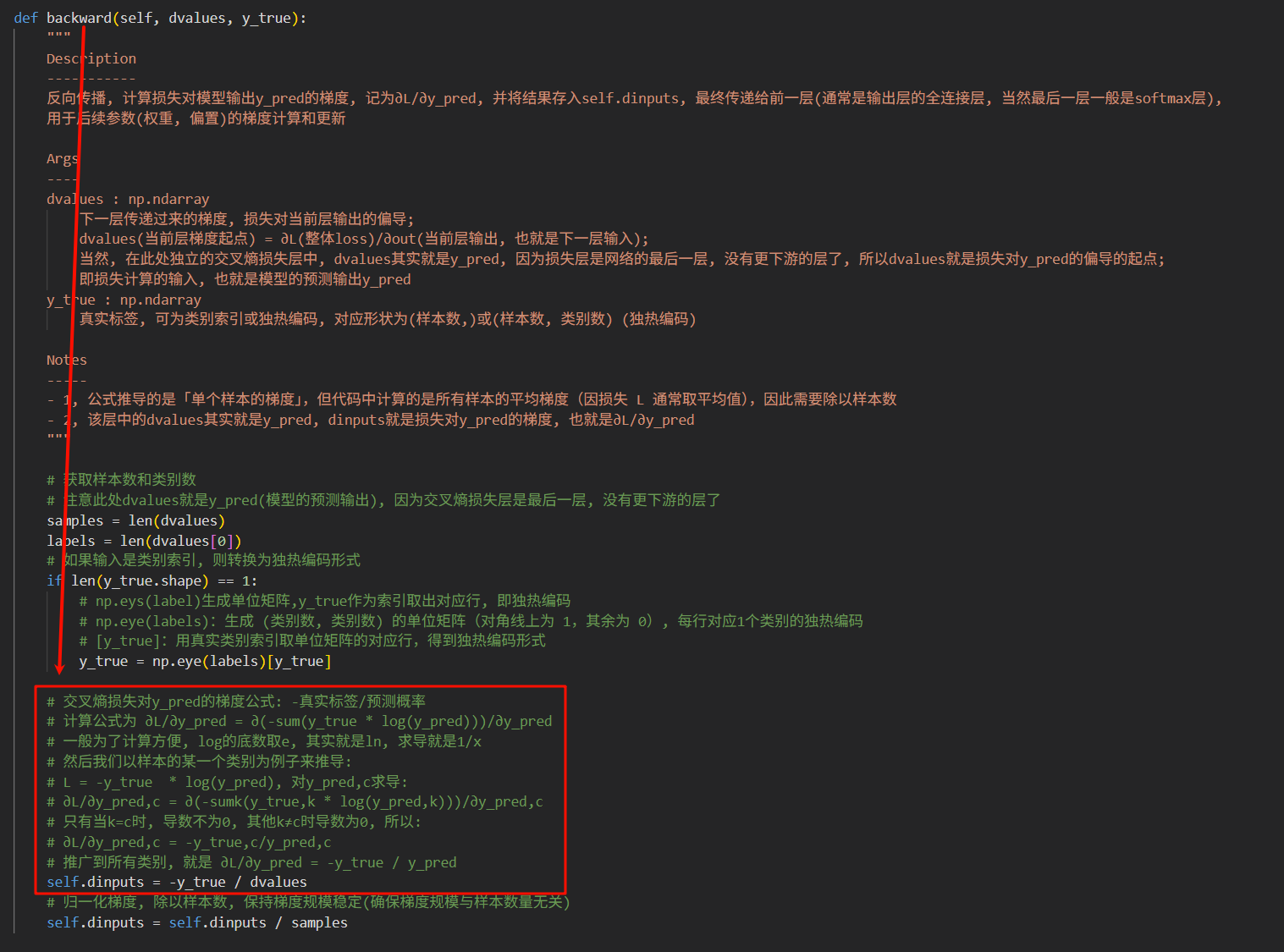
这里我们再推导一下,因为文本注释写得可能没有那么详细

再接着就是推导
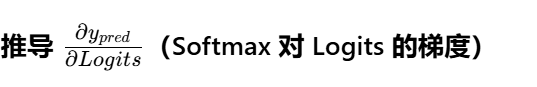

这里要分两类,本质上也只是矩阵求导中,我们实际的1个计算过程的拆分,
对于矩阵求导部分,可以查看我之前的博客(一篇简单、速成的扫盲贴):矩阵微积分速通

我们以单样本视角来看,实际上就是以类向量对列向量求导,然后我们用定义法(详情见前面提的博客)在拆分单个元素(也就是softmax中某一类的输出标量,对logits中某一类的输入标量,的一个求导),然后这里拆分出来的两个标量其实都有类别的索引,一般分析时我们就会考虑这两个类别的分类(就是简单的分类讨论逻辑,没什么特殊的)

然后这两类实际的讨论情况如下




最后的合并以及归一化

简单来说,计算出来的结果其实就是"简化之后的梯度也就是softmax+交叉熵的联合梯度 = 预测概率 - 真实标签(独热编码形式)"。
也就是对每个样本的 "真实类别对应的概率" 减 1, 等价于将独热编码的 y_true 中 "1" 的位置减 1, "0" 的位置不变。
在代码上很容易实现,就是

为什么要合并softmax和多分类交叉熵损失?
之所以把这一块证明、分析以及代码单独拿出来讲,其实是有原因的:
我们先来单独看一下如果不把softmax层和交叉熵损失层合并在一起,其损失函数是怎么样的,然后合并之后计算损失又是怎么样的?
在多分类任务中,模型输出层的结构分为两种形式,对应两种计算方式:
| 计算方式 | 网络结构 | 损失计算流程 | 梯度计算流程 |
|---|---|---|---|
| 分离计算 | 全连接层 → Softmax 层(独立) → 交叉熵损失层(独立) | 先算 Softmax 得到 ypre__d ,再代入交叉熵公式算损失 L | 先算损失对 ypred 的梯度,再算 ypred 对 Logits 的梯度,通过链式法则串联(也就是loss对out_softmax,out_softmax对in_softmax) |
| 合并计算 | 全连接层 → Softmax + 交叉熵组合层(统一) | 直接基于 Logits 推导合并后的损失公式,无需显式计算 ypre__d | 直接推导损失对 Logits 的联合梯度,跳过中间步骤(loss直接对in_softmax) |
两种方式的「最终损失值完全相等」(数学上等价),差异仅在于「计算过程」「数值稳定性」和「计算效率」。
对于前者:


尽管数学上等价,但是我们实际的工程实现中其实是将这两者合并在一起的!
参考:https://discuss.pytorch.org/t/multi-class-cross-entropy-loss-and-softmax-in-pytorch/24920/4
(该贴为pytorch官方论坛)
比如说,在pytorch中,多分类任务,nn.CrossEntropyLoss实际上已经在内部应用了F.log_softmax和nn.NLLLoss,所以我们在写代码的时候,一般直接传递原始raw logits进去就行了,也就是in_softmax。

道理很简单,分离计算有隐患


如果硬是要单独操作的话:

当然,有些时候我们不一定需要loss,可能我们只是简单的将softmax的中间输出值,作为我们另外一个网络模块的输入,或者是什么其他的运算,这是很常见的


梯度爆炸与梯度消失
总而言之,分离计算,比较容易遇到我们常说的梯度爆炸、梯度消失问题。
梯度爆炸、梯度消失其实是反向传播中梯度的两个极端问题(对应 "值极大 /inf" 和 "值极小 / 接近 0")。
当然,我们这里提到的softmax+交叉熵分离计算的梯度爆炸inf,只是梯度爆炸的一种特殊场景(数值溢出型),
深度学习中更普遍的梯度爆炸/消失,本质是链式法则累积导致的梯度幅值异常(非单纯数值计算溢出)。
梯度消失和梯度爆炸是深度神经网络训练中的常见问题,都源于反向传播过程中梯度的累积效应(累积是因为链式法则反向传播梯度):
- 梯度消失时,梯度变得极小以至网络浅层权重几乎不更新,导致学习停滞;
- 梯度爆炸时,梯度呈指数级增长,权重更新过大,使模型不稳定,无法收敛。
二者本质相同,都是由于深度网络中各层梯度(尤其是激活函数导数)连乘导致的,前者是值小于1的连乘,后者是值大于1的连乘。
梯度消失(vanishing)

loss 变化被压缩,本质是梯度在反向传播时逐层衰减,因为梯度是参数更新的依据(θ=θ−η⋅∇L),这就意味着靠近输入层的参数梯度会变得极小,甚至趋近为0。
这就导致输入层参数的更新步长几乎为0,这意味着不管loss怎么变,这些参数都"纹丝不动",相当于这部分网络层"罢工"了,没法学习输入的特征。
简单粗暴的理解:就是信号(梯度)在传递过程中被衰减到失效,相当于输入端接收不到loss变化的信号。
梯度爆炸(exploding)

梯度爆炸是梯度在反向传播时逐层放大,靠近输入层的参数会拿到一个极大的梯度值。
这会让参数更新步长变得超大,一次更新就可能让参数值偏离到离谱的范围,甚至跳出合理的数值区间(比如出现 NaN)。
比如说一个很典型的表现,就是"参数频繁修改方向",因为过大的步长可能会让模型在最优解附近来回震荡,根本没法收敛。
简单总结来说就是,梯度消失是梯度太小--->参数不更新,梯度爆炸是梯度太大--->参数乱更新,两者都是反向传播时梯度传递出了问题。
解决方法
既然提到了这些常见的问题,也就汇总一下网络上的一些普适性结局方法
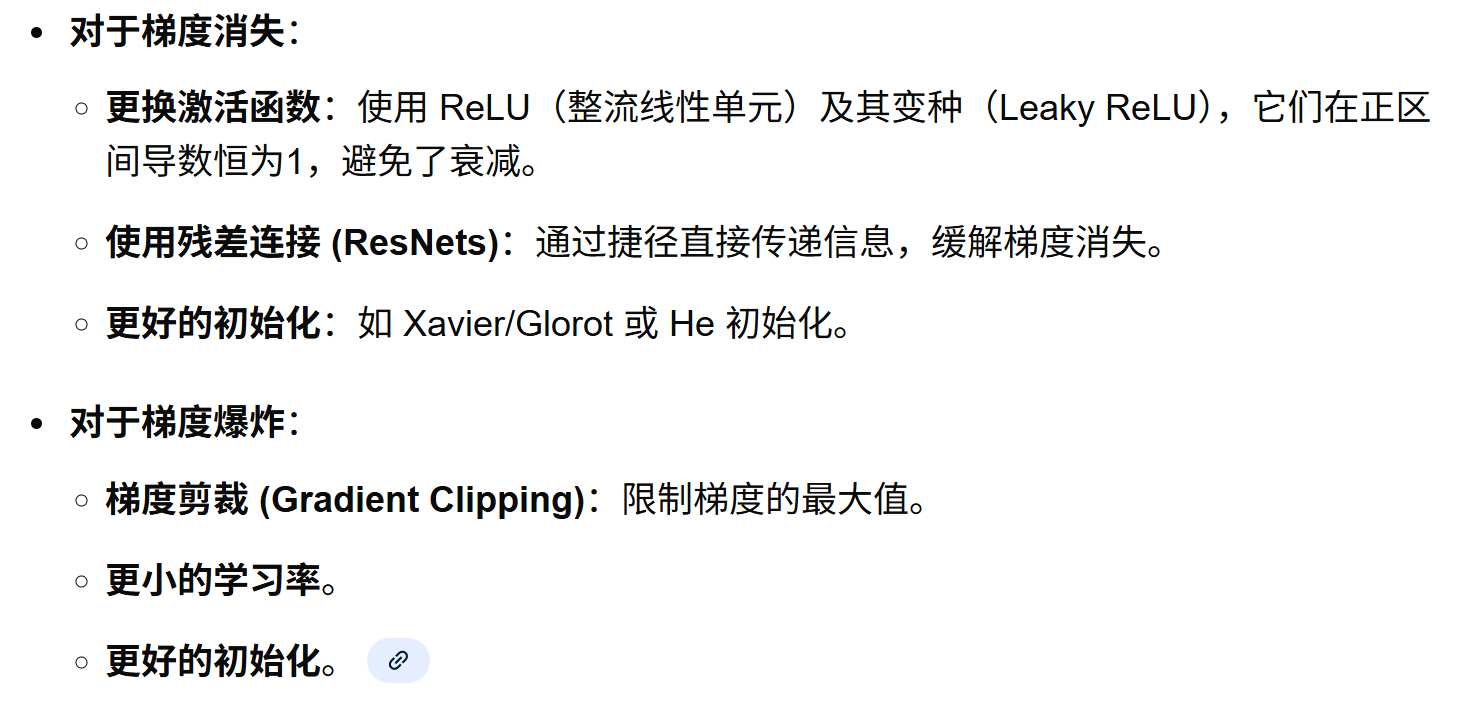
| 对比维度 | 梯度消失 (Vanishing Gradient) | 梯度爆炸 (Exploding Gradient) |
|---|---|---|
| 核心现象 | 反向传播时梯度逐层连乘衰减,趋近于 0 | 反向传播时梯度逐层连乘放大,呈指数级增长 |
| 主要影响 | 输入层参数更新停滞,模型无法学习深层特征 | 参数更新步长过大,训练震荡不收敛,甚至出现 NaN |
| 核心原因 | 1. Sigmoid、Tanh 等激活函数在饱和区导数接近 02. 多层网络梯度连乘后急剧衰减 | 1. 权重初始化值过大2. 部分激活函数导数大于 1,多层连乘后梯度失控 |
| 激活函数优化 | 1. 使用 ReLU 及其变体(ReLU、Leaky ReLU、ELU):导数在非负区间为 1,避免梯度衰减2. 替换 Sigmoid/Tanh 为更平缓且导数区间更大的函数 | 1. 避免使用导数恒大于 1 的激活函数2. 优先选择 ReLU 系列,其导数最大为 1,可限制梯度放大 |
| 权重初始化策略 | 1. Xavier 初始化:适用于 Tanh/Sigmoid,使每层输入输出的方差一致2. He 初始化:专为 ReLU 设计,适配其单侧激活的特性 | 1. 小范围权重初始化:避免初始权重过大,减少梯度连乘的放大效应2. 采用 Xavier/He 初始化,控制每层梯度的传播幅度 |
| 梯度裁剪 (Gradient Clipping) | 一般不适用(梯度本身已趋近于 0) | 核心解决方法:设置梯度的最大阈值,当梯度超过阈值时,将其裁剪到阈值范围内,防止梯度无限放大 |
| 网络结构改进 | 1. 残差连接 (ResNet):通过短路连接,让梯度直接传递到浅层,避免梯度衰减2. 分层训练 / 预训练:先训练浅层网络,再叠加深层,逐层传递有效梯度 | 1. 残差连接同样有效:限制梯度在短路路径中的放大2. 减少网络深度:降低梯度连乘的层数,从根源减少放大风险 |
| 归一化手段 | 1. 批量归一化 (Batch Normalization):标准化每层输入分布,避免激活函数进入饱和区,维持梯度活性2. 层归一化 (Layer Normalization):适配小批量场景,效果类似 | 1. 批量归一化 / 层归一化:稳定每层输入输出的方差,限制梯度的异常波动2. 权重归一化:对权重进行归一化处理,降低梯度放大的可能性 |
| 优化器调整 | 1. 使用 Adam、RMSprop 等自适应学习率优化器:自动调整参数的学习率,即使梯度小也能有效更新2. 适当提高学习率(需配合其他策略) | 1. 降低全局学习率:减小参数更新步长,缓解震荡2. 使用 Adam/RMSprop:通过梯度平方的滑动平均,抑制过大梯度的影响 |
一些题外话
首先是数学符号说明,都是一些微积分中简单的符号
- 向量微积分的梯度算子/Nabla算子:
倒立三角形 ∇(Nabla 算子)≠ 普通导数,而是 "梯度算子"
参考:https://zh.wikipedia.org/wiki/向量算子
https://zh.wikipedia.org/wiki/倒三角算符

学过微积分的,应该在多元微积分中会经常遇到这个向量运算符的各种奇形怪状的形式,比如说衍生出的梯度、散度、旋度等等等。

- 其他的类似:
- 哈密顿算子:
实际上我们在大学物理(比如说工科生基础的电动力学或者是一些基础的电磁力学)中,经常会遇到的一个算符,其实本质上就是Nabla算子,就是向量微分算子,只不过我们都知道数学中的向量,在物理中对应的矢量,那每一个都有很多故事,所以内涵会更丰富一点。


- 拉普拉斯算子:参考[https://zh.wikipedia.org/wiki/%E6%8B%89%E6%99%AE%E6%8B%89%E6%96%AF%E7%AE%97%E5%AD%90](https://zh.wikipedia.org/wiki/%E6%8B%89%E6%99%AE%E6%8B%89%E6%96%AF%E7%AE%97%E5%AD%90)

梯度消失与Dead Neuron、Dropout等
问题不一定直接相关,但是多思考这些深度学习中常见的术语,从计算逻辑层面上去思考,对于深度学习还是有益的。
本质上:
- 梯度消失是被动导致神经元/层失效
- Dead Neuron是神经元永久失效的状态
- Dropout是主动让部分神经元暂时失效以预防过拟合
| 概念 | 核心定义 | 本质属性 | 发生场景 |
|---|---|---|---|
| 梯度消失 | 反向传播时,梯度(参数更新的依据)从输出层向输入层逐层衰减,最终趋近于 0 | 「梯度传递问题」 | 深层网络(如未用残差连接的 CNN、早期 DNN) |
| Dead Neuron | 神经元在训练中永久 "失去活性"------ 无论输入是什么,输出始终为 0(或趋近于 0) | 「神经元失效状态」 | 激活函数选择不当(如 Sigmoid)、梯度消失 / 爆炸 |
| Dropout | 训练时随机 "关闭"(输出置 0)一部分神经元,测试时恢复并按比例缩放权重 | 「正则化策略」 | 几乎所有深度学习模型(预防过拟合) |
梯度消失 ↔ Dead Neuron:"因" 与 "果" 的关系
梯度消失是导致 Dead Neuron 的核心原因之一,两者是 "问题根源" 与 "最终失效状态" 的直接关联。
我们以sigmoid函数为例,依据微积分,我们可以轻易地求出其一阶导、二阶导,并做一些极值点的分析(一阶驻点、二阶拐点)

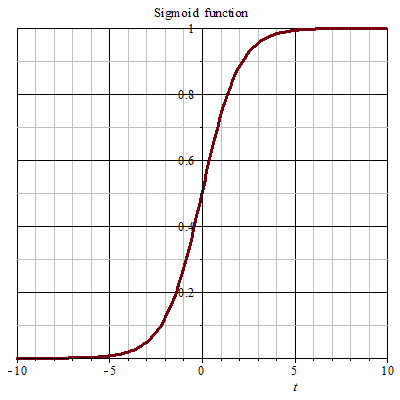 、
、


Dropout ↔ 梯度消失 / Dead Neuron:"缓解工具" 与 "问题" 的关系
Dropout 是深度学习中经典的正则化策略,其核心目的是预防过拟合,但在设计上也能间接缓解梯度消失,并降低 Dead Neuron 的风险 ------ 注意:Dropout 不直接 "解决" 梯度消失,而是通过改变网络结构的 "冗余性" 来减轻影响。


为什么要修正动量偏差?
动量公式大家都理解,至少从实现细节的背景需求,以及数学逻辑上。
但是问题是:我们前面的模板代码中还有修正动量的地方

那么问题来了,我们为什么要修正偏差?
- 首先是,哪里来的偏差?
- 其次是,为什么需要修正偏差,保留不行吗,或者我们确实能够评估它的影响程度?
- 如何修正偏差?
首先,哪里来的偏差?
我们需要了解我们动量计算的是什么,缓存存储的是什么,和什么标准进行比较,又为什么会有偏差?
下面这个是我们每一次迭代中更新的动量数组,
可以看到我们更新的方法,受历史动量与当前迭代的梯度影响。
然后权重和偏置,其实更新的逻辑是一致的,所以我们单独拿权重来讲。

首先我们需要明确的是,我们为什么需要动量?
我们之所以需要动量,是因为我们想要通过"历史梯度的加权平均"来平滑梯度的波动(无论是方向还是模长)。
为什么要平滑这种梯度的迭代变化?
因为SGD的原始优化算法有问题。动量设计的目的,其实就是为了解决SGD梯度波动大、更新方向不稳定的问题,
我们原始的参数更新公式,就是完全依赖于梯度信息(θ=θ−η⋅∇L),
如果说SGD可能在某一步梯度突然变大、变小、方向突变,导致训练震荡,无法收敛。
而动量,能够通过积累历史梯度的信息,让当前梯度对于参数更新的影响,能够被历史梯度所稀释一下,也就是让参数更新的方向和模长能够更稳定。

更通俗易懂地解释,可以参考李宏毅老师对于动量法的介绍:
https://www.youtube.com/watch?v=zzbr1h9sF54&t=9s
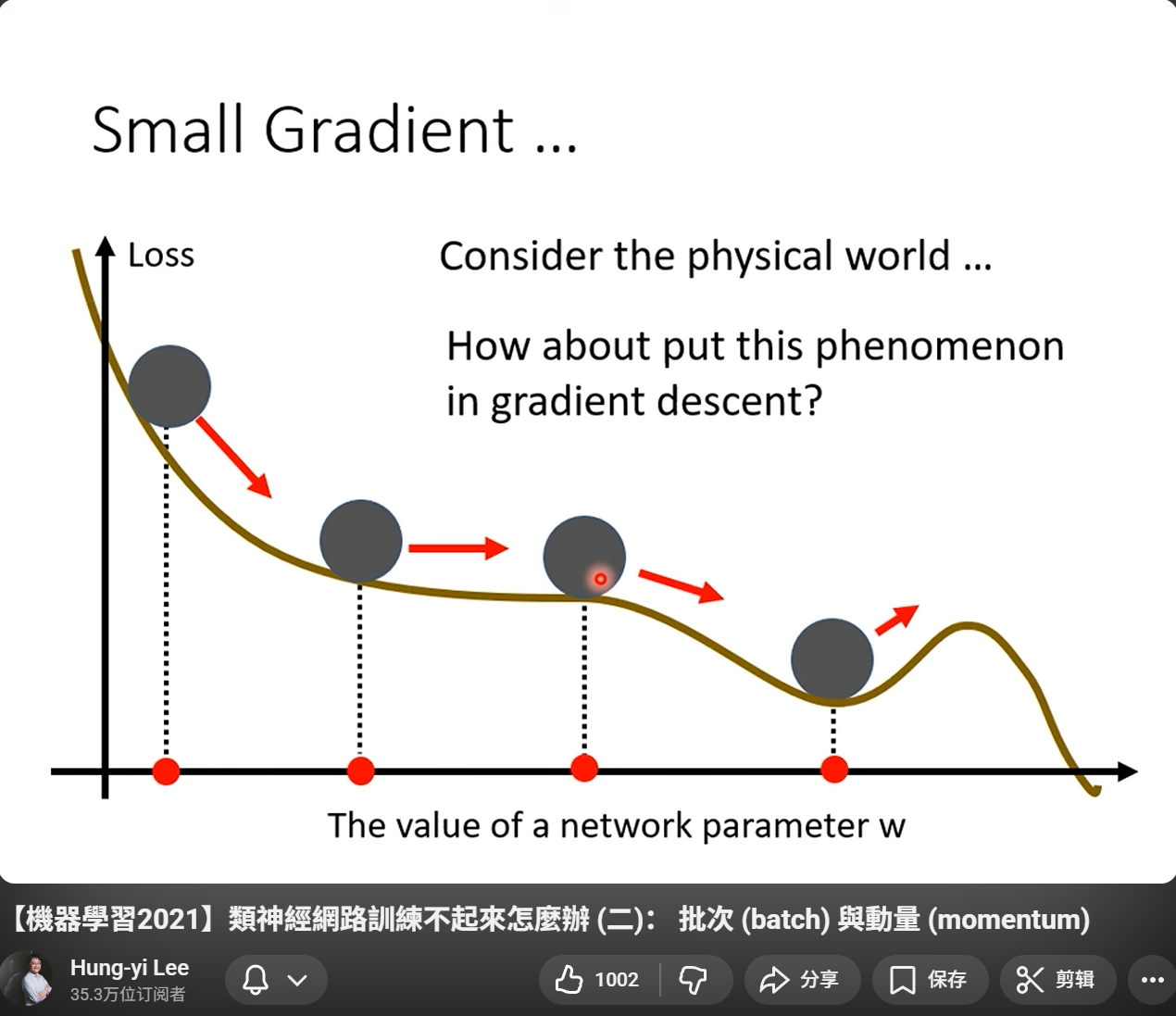
以及自适应学习率(给每一个参数设置不同的学习率)
https://www.youtube.com/watch?v=HYUXEeh3kwY&t=157s
李老师讲动量法,同样是从SGD缺陷开始讲的:
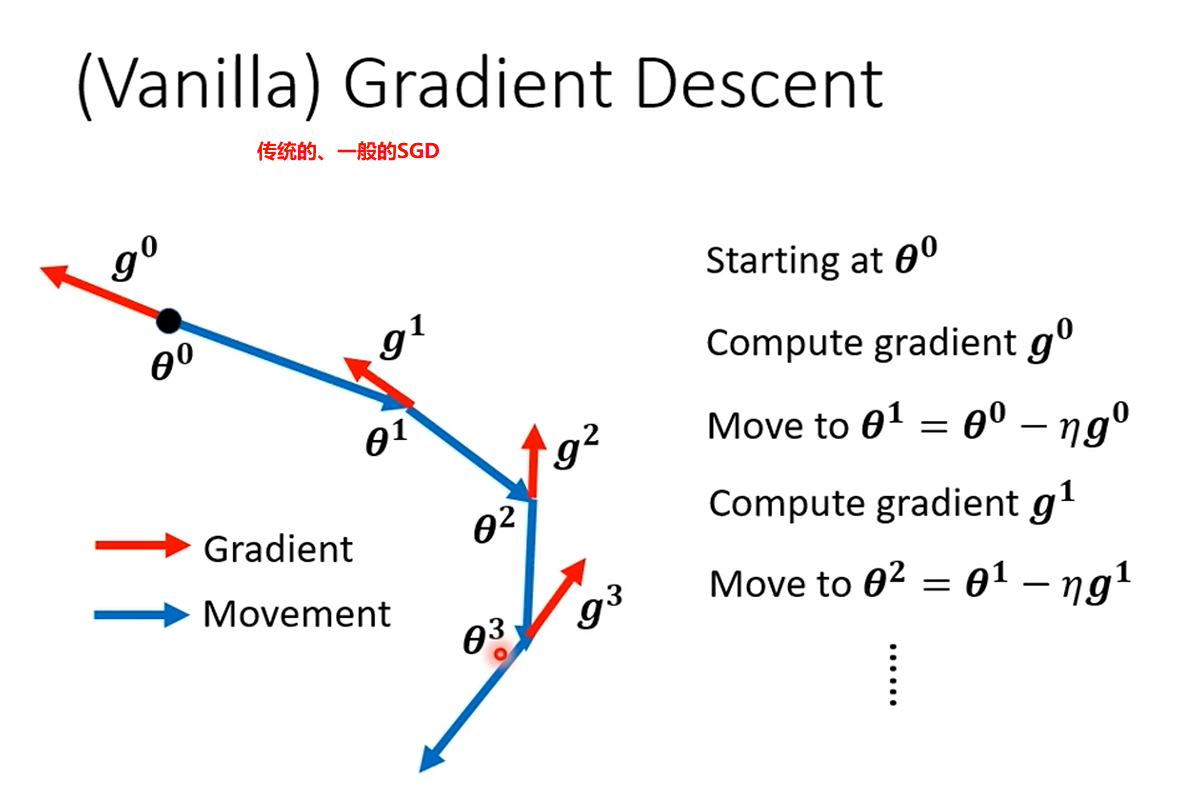
初始没有惯性,所以m0=0,也就是对应我们代码中的动量初始化设置为0
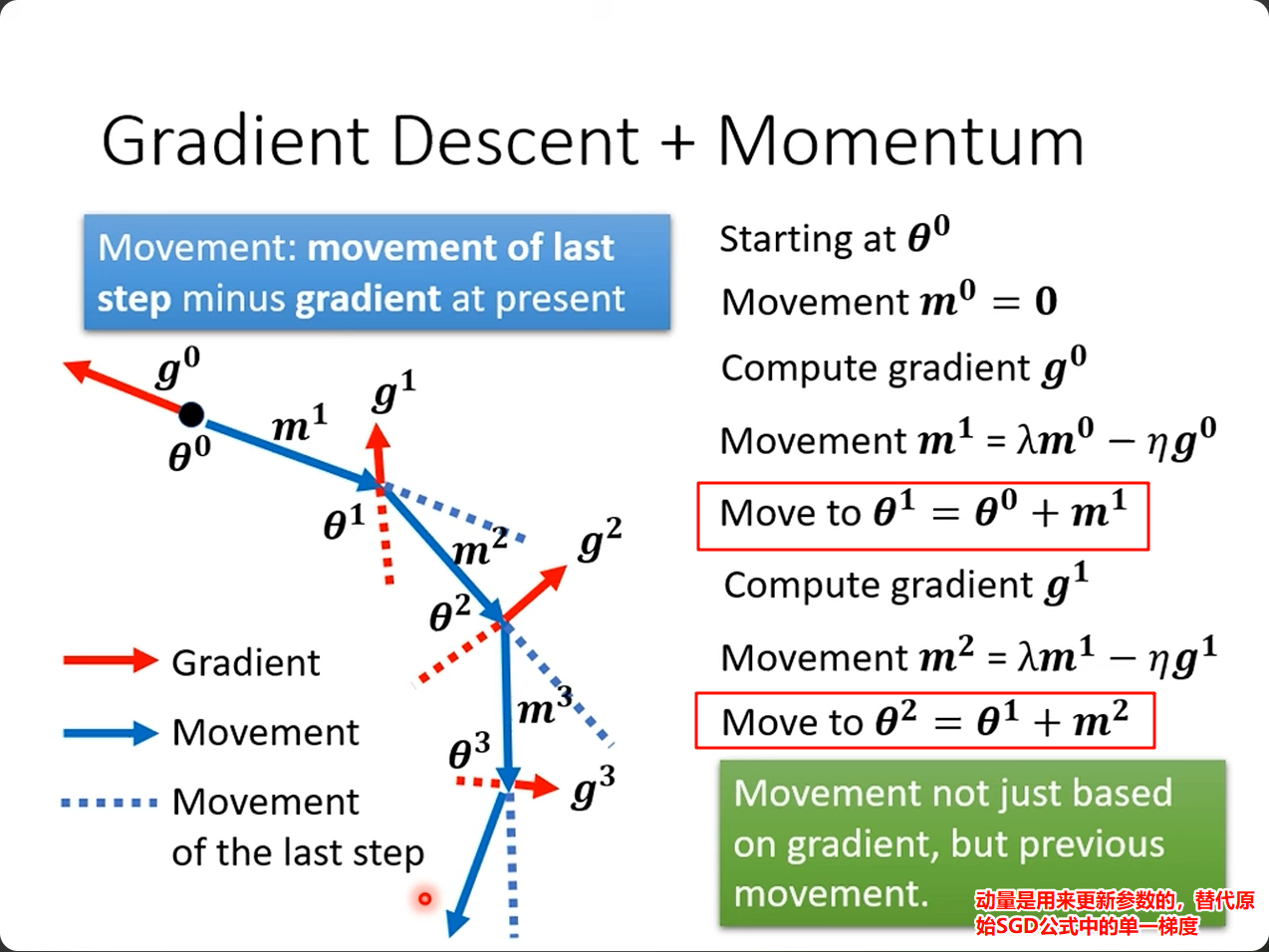
动量的数学意义就是所有历史梯度信息的一种加权平均

最经典的就是下面这张图了:
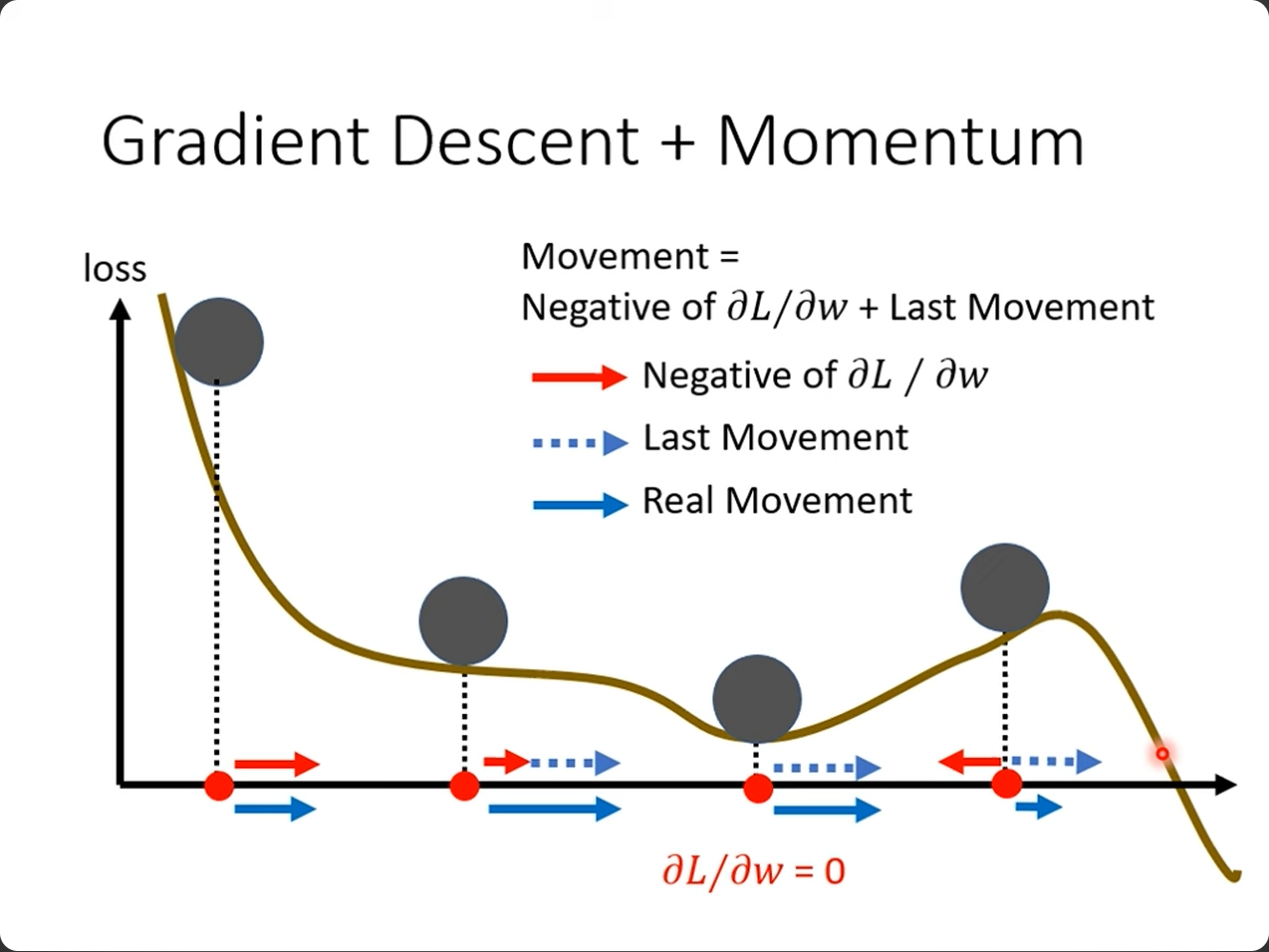
我们用"走路下山"的生活例子,把「原始SGD公式」「动量」「缓存」的逻辑关系串起来(θ是我们当前的位置,目标是走到山底=最小化损失):
1. 原始公式(θ=θ−η⋅∇L):"只看脚下,步长固定"
原始SGD的逻辑像"蒙眼走路":
- ∇L(当前梯度)= 我们脚下的"坡度方向"(比如脚下路往东北斜,梯度方向就是东北,我们往反方向西南走);
- η(学习率)= 我们固定的"步长"(比如每次迈0.5米);
- 公式意思:看脚下的坡度,往反方向迈固定步长。
但这个方式有两个大问题:
- 问题1:路坑坑洼洼(梯度波动大)→ 我们会左摇右晃(训练震荡),走不稳;
- 问题2:路是缓坡但很长(梯度小但方向稳定)→ 我们迈小步慢慢挪(收敛慢),到不了底。
2. 动量(对应代码里的weight_momentums):"加上惯性,走得更稳更快"
为了解决"摇摇晃晃+走得慢",我们给走路加个"惯性"(动量):
- 动量=我们"之前走的方向的积累"(比如前几步一直往西南走,就有了西南方向的惯性);
- 现在的更新逻辑:看脚下的坡度 + 之前的惯性,往这个混合方向迈步。
对应公式(动量版更新):
θ = θ - η \\cdot m_t
其中 m_t = β_1 \\cdot m_{t-1} + (1-β_1) \\cdot ∇L ( ( ( m_t 是当前惯性, 是当前惯性, 是当前惯性, m_{t-1} 是之前的惯性)。
像走路时:
- 如果我们前几步一直往西南走(惯性方向),现在脚下稍微往南偏了一点(当前梯度),我们不会突然拐向南,而是带着西南的惯性,往"西南偏南"走------既稳(不晃),又快(惯性帮你加速)。
代码里的weight_momentums:就是记录"惯性"的小本本。首次更新时(我们刚起步),还没有任何惯性,所以用全0数组初始化(小本本是空白的),之后每走一步,就把"当前坡度+之前惯性"记到这个小本本里。
3,自适应学习率的问题
但是这里还有一个问题,就是自适应学习率的问题:
当我们训练一个network,然后loss不再下降的时候,我们并不一定是卡在局部最小值点/saddle point,不一定是收敛了,也有可能只是单纯的loss没法下降(这个时候可以分析一下梯度的范数,看看到底卡住的原因是什么)

比如说可能是左边这种震荡,一直无法收敛;
更具体地,李老师举了一个凸优化的例子(一个椭圆形error surface)
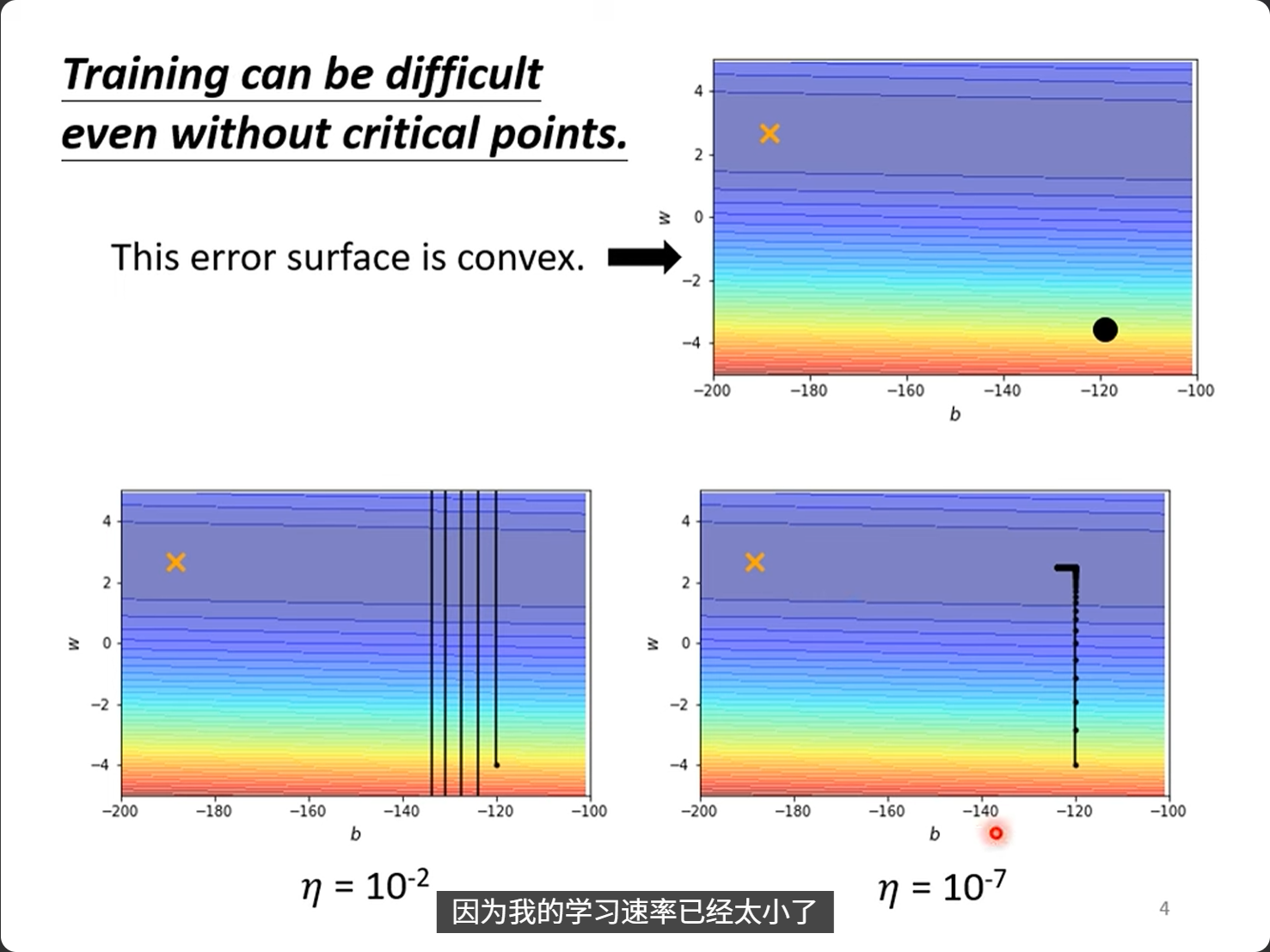
在短轴处需要设置小学习率,才能慢慢沿着误差曲线下滑(上面右图),否则就是快速震荡了(上面左图)。
但是一旦滑到平原地区,此时的学习率,如果还是固定的话,那么在椭圆长轴区域,就已经很难移动了(参数迭代速度会非常慢)。
这就是典型的学习率一刀切问题,没有"看碟下菜",也就是随机应变。
那么如何随机应变呢,我们需要的就是自适应学习率,也就是给不同参数设置不同的学习率(学习率的值随着参数值的变化而变化)
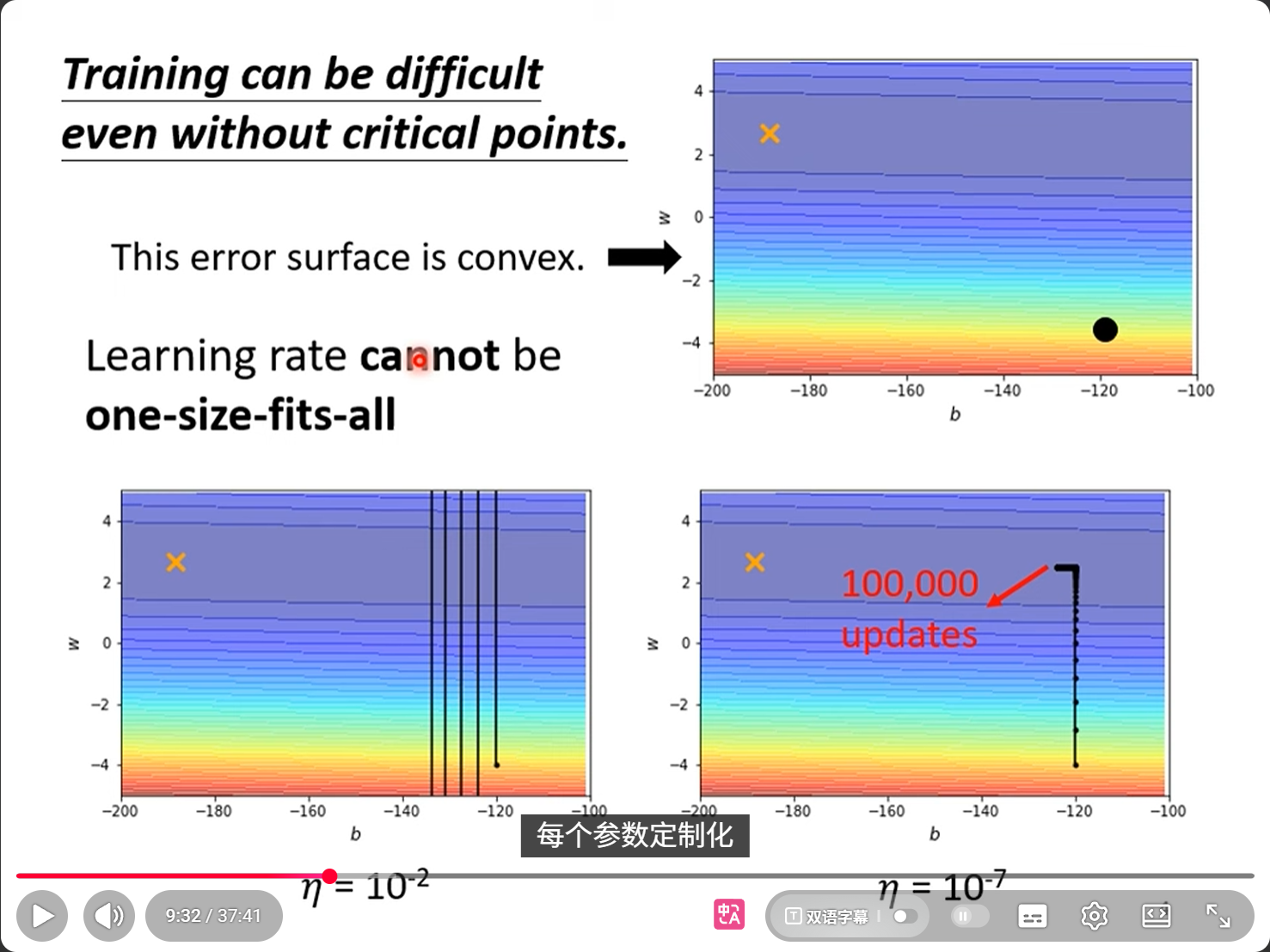
那么如何做到定制化的学习率呢?
答案就是在参数的迭代更新公式中引入新的变量(这个变量和参数有关,而我们的参数,比如说下面的θi,就是指第i个参数,t上标指的是第t轮迭代------》要让更新也就是这个新学习率和参数相关、参数定制化,那么我们加入的这个参数δ,也得和i、t相关,也就是绿色框框出来的两个)
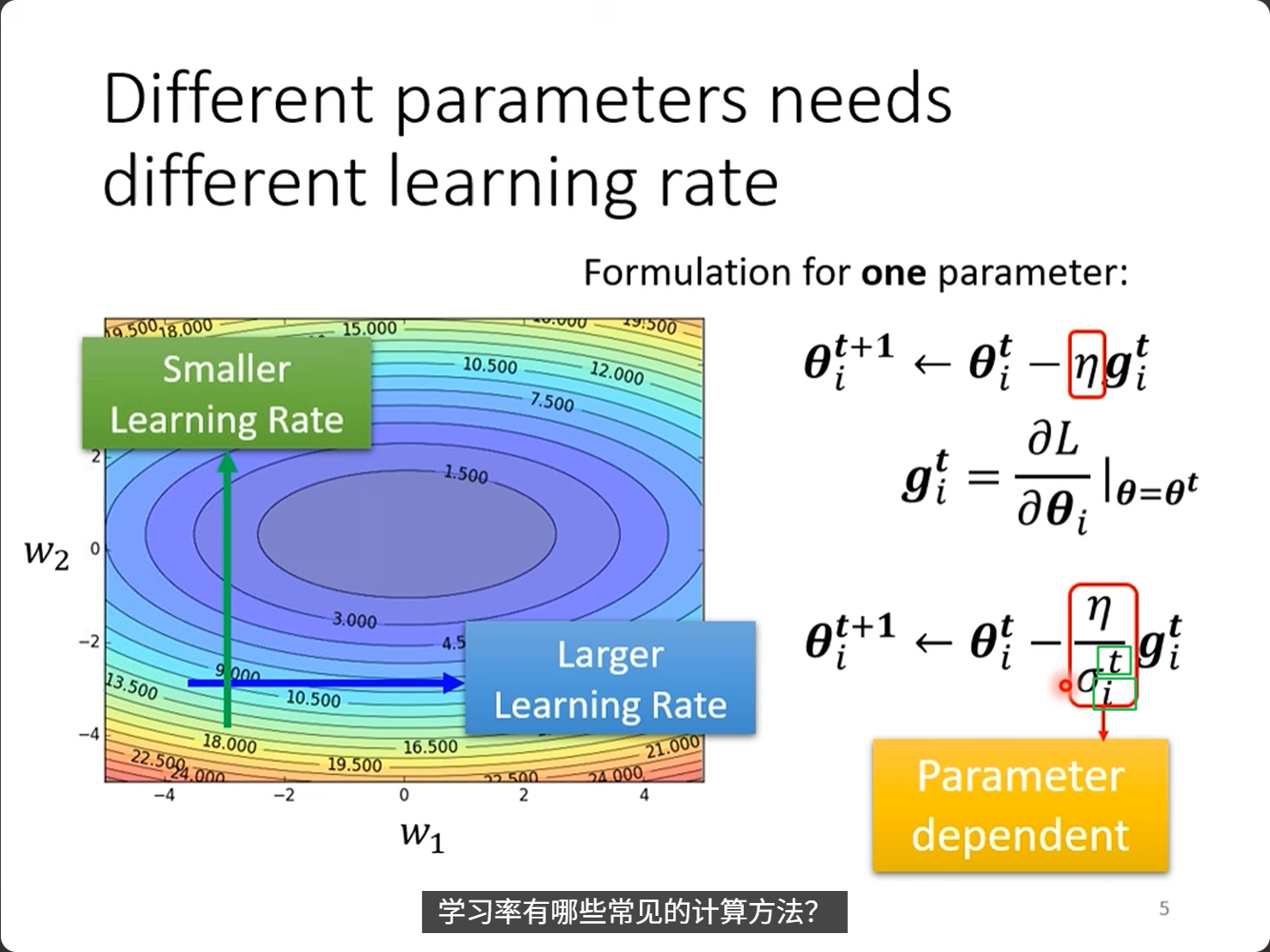
具体来说:我们新引入的δ这个变量就是历史梯度信息的均方根(平方和的均值的平方根)
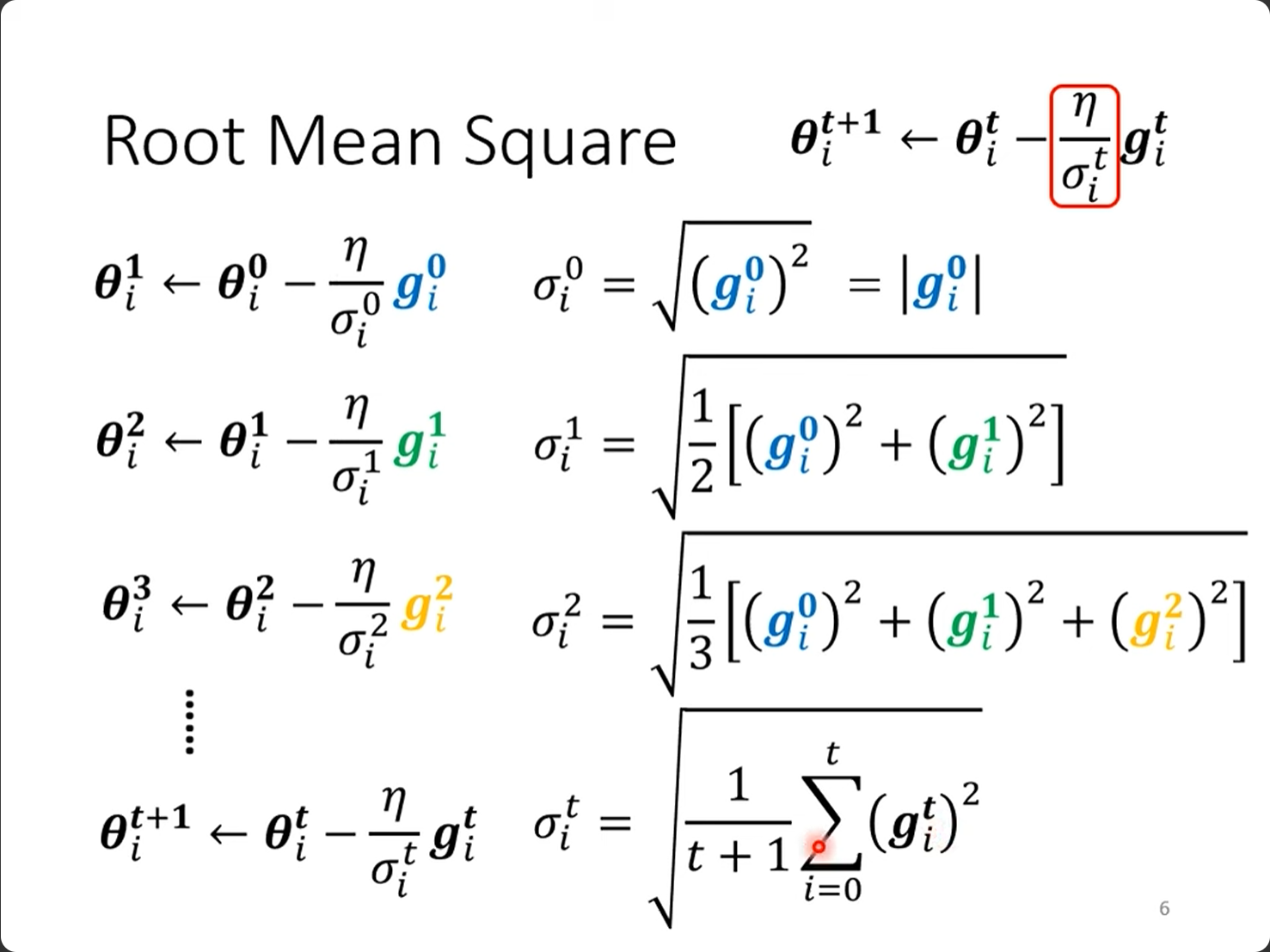
而这个RMS均方根的方法,就是Adagrad。
也就是能够做到,在error surface中,遇到坡度大梯度大的地方,学习率调小慢慢走;遇到坡度小梯度小的地方,学习率调大走快一点。
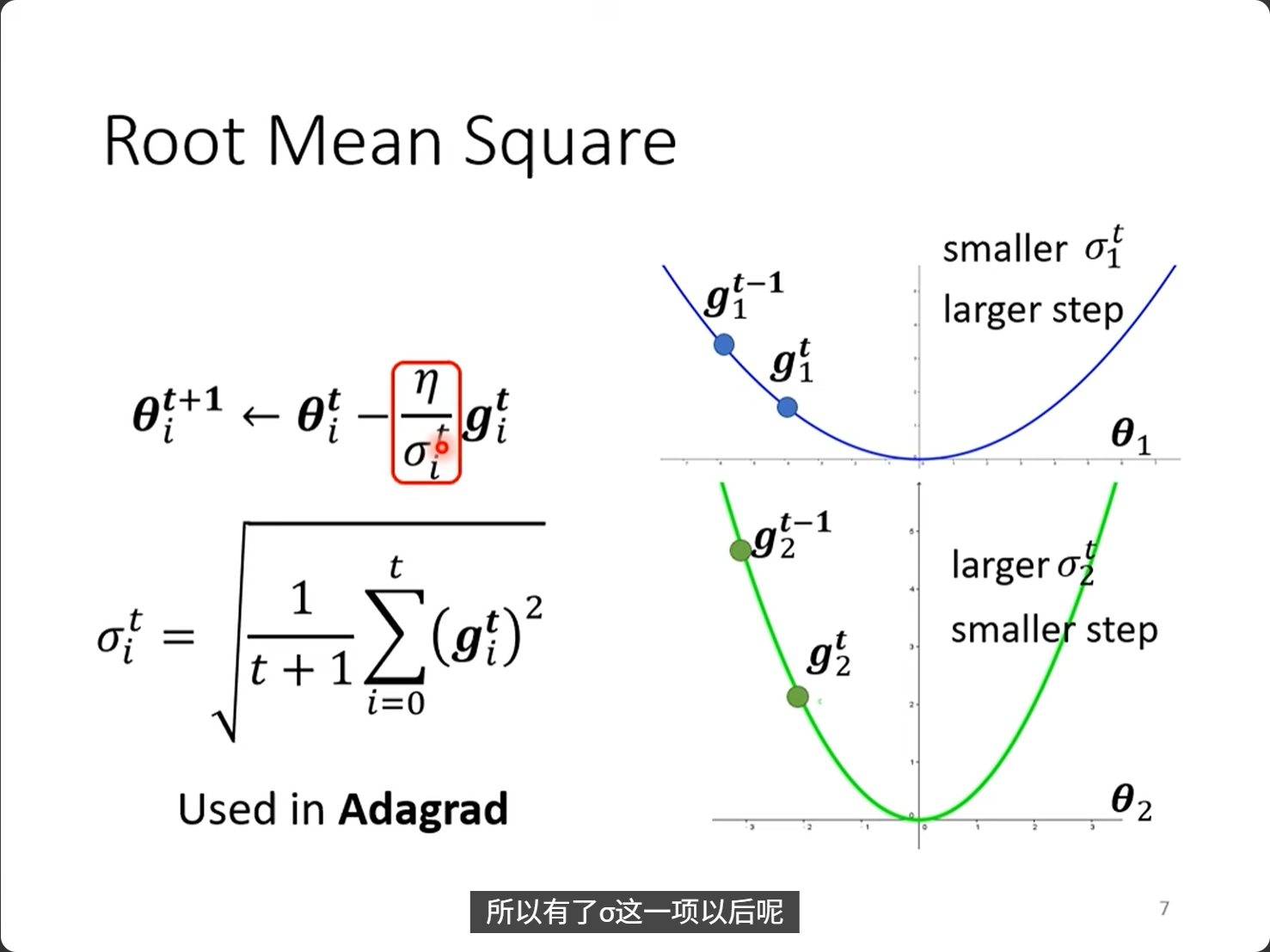
虽然上面的这个Adagrad的方法已经能够做到对于一个参数在不同迭代中调整学习率了,但这个方法并不是我们今天所使用的最终版本。
我们再来看一下这个逻辑,我们这里学习率更新的依据,是因为参数θi在不同的迭代次数中(t不同中)引入了新的梯度gt,所以我们的学习率才会变,所以θt参数更新才会有和上一轮不同的操作;
所以实际上δ这个分母是依据梯度自动调整学习率大小。
而我们在Adagrad中的假设,其实有一点,是假设只要是同一个参数θi,其梯度大小gi的历史贡献是相同的,因为我们均方根公式是最简单的加权平均(所有权相等),每一个梯度gt都有同等重要性。
那么新的方法,也就是下面的RMSPro做了什么呢?
调整了当前迭代中当前梯度的重要性,原理是一样的,还是历史梯度的加权,只不过每一次迭代的梯度的权重(也就是我们认为的重要性)不一样了,通过α这个参数来调整当前梯度对于当前迭代的影响大小。

一个很经典的说明示例还是走路下山:
当我们走在平路上,然后突然进入到陡坡,这个时候梯度突变变大,我们其实可以迅速调大该轮迭代中梯度的影响(也就是将α调小,gt的比重调大),然后这个时候δt就会变得很大,然后学习率整体就会变小,结果就是我们在陡坡上迅速降低速度慢慢走(也就是迅速踩刹车)。
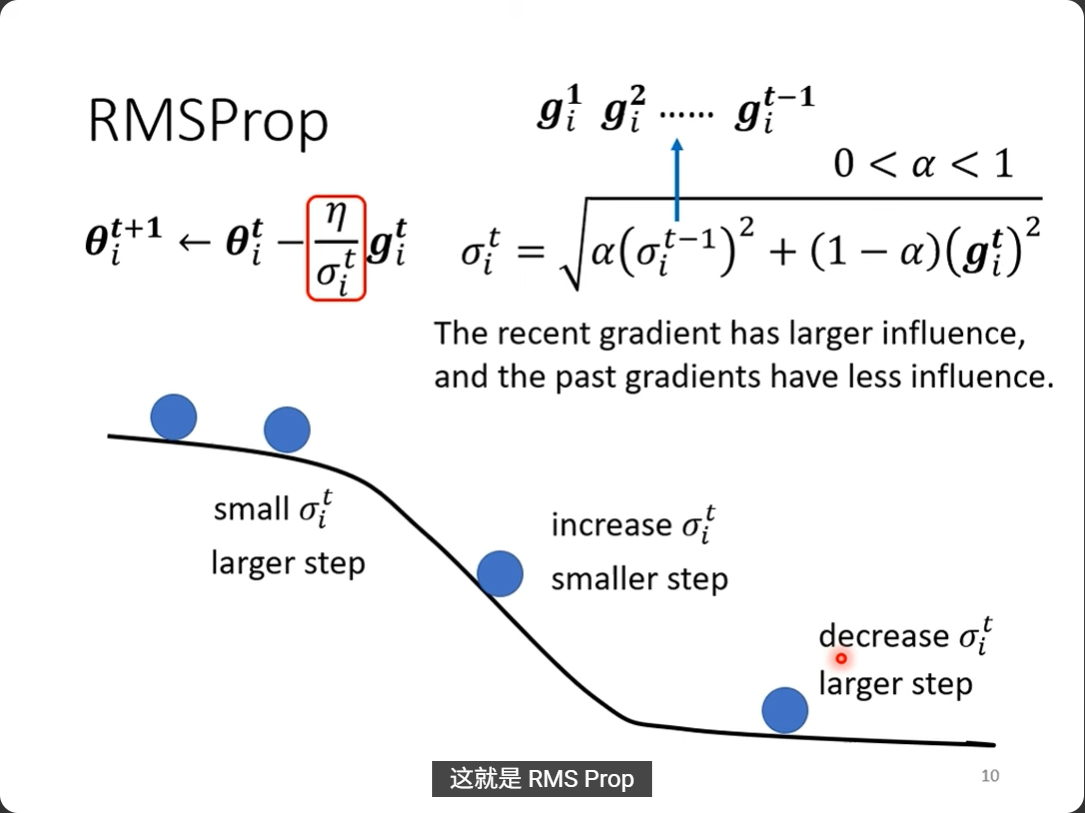
讲完了动量法和RMSProp,我们再来看一下现在深度学习常用的优化算法,也就是SGD的一个优化版本,Adam算法,实际上就是RMSProp(自适应学习率)+动量法(考虑历史梯度),
其实说白了,就是学习率要考虑历史信息、梯度也要考虑历史信息,考虑的东西越多、参数能够调整的空间越自由(附加的超参数越来越多)

具体可以参考pytorch中的实现:https://docs.pytorch.org/docs/stable/generated/torch.optim.Adam.html
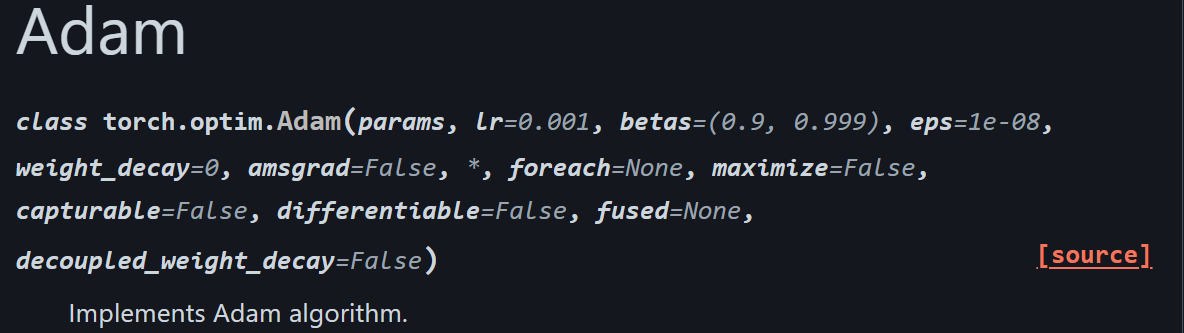

依据原始文献:https://arxiv.org/abs/1412.6980
现在回过头再来看一下我们的模板代码,
下面这一块是动量法(梯度需要考虑历史信息):


下面这一块是RMSProp,也就是自适应学习率(学习率需要考虑历史信息):

都是梯度的平方量纲

4. 缓存(对应代码里的weight_cache):"看之前的步长,灵活调整迈腿大小"
原始SGD和动量的步长都是"固定的η",但走路时有时需要"灵活调步长":
- 如果你之前踩过"陡坡"(梯度大=步长大),现在就要迈小步(防止踩空);
- 如果你之前走的是"缓坡"(梯度小=步长小),现在就要迈大步(加快下山)。
这就是缓存的作用:记录"之前步长的大小",动态调整当前步长。也就是动态调整学习率,自适应学习率,上面已经提过了。
我们关注的点是,现在Adam的公式和理论我们清楚了,动量法和RMSProp的代码实现我们前面比对了,那么合并起来的Adam呢?
代码中是这一块:

代码中对应公式(加缓存后的更新):
θ = θ - η \\cdot \\frac{\\hat{m}_t}{\\sqrt{\\hat{v}_t} + ε}
其中 \\hat{v}_t (修正后的缓存)= 我们"之前步长大小的平均"。
现在我们来严格比较一下这两个公式
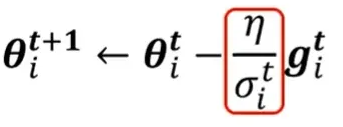
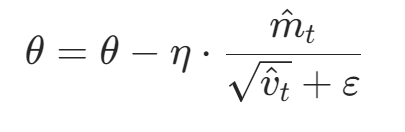
首先学习率的调整,也就是分母处引入的RMSProp项,查看代码以及形式是没问题的,加一个伪计数项防0影响不大;
梯度的调整,也就是我们现在的历史梯度的加权平均(动量),从形式上是没问题的;
所以此处更新代码形式没问题。
为什么说梯度形式没问题,但是代码细节没提呢?
因为这个就是我们一开始提出的问题,为什么在具体实现中要调整动量(⚠️ 绕了一大圈终于回到我们前面的问题了!)
缓存cache其实就是历史信息,结合Adam,我们要更新的是两块:
1个是历史梯度,也就是动量法中需要更新的,对应矫正为

另外1个是历史学习率,也就是RMSProp法需要更新的,对应矫正为

总体来说就是:

那么这两块为什么要修正呢?
因为我们这两块实际上计算的都是cache值,因为动量法和RMSProp法要求的实际上都是历史梯度、学习率的加权平均,也就是都需要历史信息。
加权平均,首先从数学形式上来讲,我们就得确保每一次加权的公式拆开来看所有历史迭代次数中的数据权重和为1。
道理很简单,再回过头来看一下我们的代码:
下面这一块是动量法(梯度需要考虑历史信息):
我们的权重每一次迭代确实看起来β1、1-β1是加权和为1的


下面这一块是RMSProp,也就是自适应学习率(学习率需要考虑历史信息):
同样看起来β2、1-β2是加权和为1的

都是梯度的平方量纲

但是但是!虽然β12、1-β12是看起来加权和为1!
但是我们初始化的时候:动量和学习率对应项都是赋值为0!
也就是说,我们只需要简单用t=0去检验一下上面的动量法和RMSProp法的公式,一旦代进去,只要历史信息t=0的时刻值,一旦代进去,就是0(因为t=0时刻的历史值就是0),所以相当于这一项的权是没有的,
那么我们后面再一次一次迭代加权,实际上都是在"加权和不为1"的这么一个最基础的数学错误上进行的,所以需要进行矫正!

比如说以权重参数更新为例,我们看梯度也就是动量法迭代:

然后因为我们的代码中cache(学习率历史)、动量(梯度历史)都是初始值赋为0,都是同样加权逻辑,所以矫正的方法自然也就一样,所以代码中两处矫正是一致的。
三者的逻辑关系(对比表)
| 方式 | 走路逻辑 | 解决的问题 | 代码里的"工具" |
|---|---|---|---|
| 原始SGD | 只看脚下坡度,迈固定步长 | 无(问题多) | 无额外工具 |
| SGD+动量 | 看脚下坡度+之前的惯性,迈步 | 走路晃(震荡)、走得慢 | weight_momentums(记惯性) |
| Adam(动量+缓存) | 看惯性+之前的步长,灵活调步长迈步 | 步长固定导致的踩空/慢走 | weight_cache(记步长) |
11,检查一下nnfs
现在我们再回过头来看一下这里的nnfs:
同样,用我之前开发的LibInspector看一下;
因为这里其实还是挂载的colab的jupyter服务器目录,所以必须得再从头安装一下
在colab上我们的工具照样能够运行:

我们把分析之后的报告文档下载下来看看
下面是解析出来的html内容: