目录
电路学习(一)
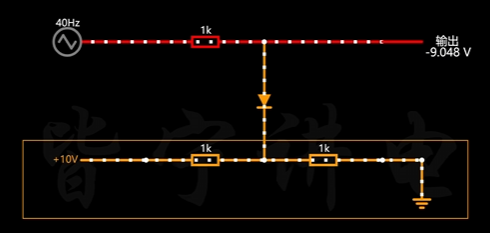
一、钳位电路
- 戴维南等效电路
二、PID的零点和极点
这是一个非常专业的问题,答案取决于我们如何定义和看待PID控制器。简单直接的回答是:一个理想的并行式PID控制器有两个零点和一个位于原点的极点。
下面我们从不同表示形式进行详细分析。
一、理想PID控制器的传递函数
最常用的并行形式(Ideal PID)的传递函数为:
G _ c ( s ) = K _ p + K _ i s + K _ d s = K _ d s 2 + K _ p s + K _ i s G\_{c}(s) = K\_p + \frac{K\_i}{s} + K\_d s = \frac{K\_d s^2 + K\_p s + K\_i}{s} G_c(s)=K_p+sK_i+K_ds=sK_ds2+K_ps+K_i
从这个公式我们可以直接分析出:
- 极点(Poles) : 令分母为零,即 ( s = 0 )。所以,系统在原点处有1个极点。
- 零点(Zeros) : 令分子为零,即 ( K_d s^2 + K_p s + K_i = 0 )。这是一个二次方程,其根的个数由判别式决定。在绝大多数实际应用中,( K_p, K_i, K_d > 0 ),这个二次方程有两个根(可以是两个实根或一对共轭复根)。因此,系统有2个零点。
结论1:一个理想的并行式PID控制器有 2 个零点和 1 个极点。
二、实际PID控制器(考虑噪声和可实现性)
理想微分环节 ( K_d s ) 在实际中是无法实现的(它对高频噪声极度敏感,且增益随频率无限增大)。因此,实际PID控制器会用一个一阶低通滤波器来近似微分项,最常见的形式是:
G _ c ( s ) = K _ p + K _ i s + K _ d s 1 + s N G\_{c}(s) = K\_p + \frac{K\_i}{s} + \frac{K\_d s}{1 + \frac{s}{N}} G_c(s)=K_p+sK_i+1+NsK_ds
这里,( N ) 是微分滤波系数,通常取值在5-20之间。将这个表达式通分合并后,传递函数变为:
- 分子 : 是一个三次多项式,因此 有3个零点。
- 分母 : 是 s ( 1 + s N ) s (1 + \frac{s}{N}) s(1+Ns),所以 有2个极点 :一个在原点 s = 0 s=0 s=0,另一个在 s = − N s=-N s=−N。
结论2:一个实际的可实现PID控制器(带微分滤波)有 3 个零点和 2 个极点。
三、其他形式的PID(串联式)
PID控制器也可以写成串联形式(Series 或 Interactive Form):
G _ c ( s ) = K ( 1 + 1 T _ i s ) ( 1 + T _ d s ) G\_{c}(s) = K \left( 1 + \frac{1}{T\_i s} \right) (1 + T\_d s) G_c(s)=K(1+T_is1)(1+T_ds)
将其改写为标准形式:
G _ c ( s ) = K ( T _ i T _ d s 2 + T _ i s + 1 ) T _ i s = K T _ d s 2 + K s + K T _ i s G\_{c}(s) = K \frac{(T\_i T\_d s^2 + T\_i s + 1)}{T\_i s} = \frac{K T\_d s^2 + K s + \frac{K}{T\_i}}{s} G_c(s)=KT_is(T_iT_ds2+T_is+1)=sKT_ds2+Ks+T_iK
这与我们最初讨论的理想并行形式在数学上是等价的(系数对应关系不同)。因此,它同样具有 2个零点 和 1个位于原点的极点。
总结与对比
为了更清晰地理解,下表总结了不同情况下PID的零极点数量:
| PID控制器类型 | 零点数量 | 极点数量 | 说明 |
|---|---|---|---|
| 理想PID(并行式) | 2 | 1 (在原点) | 理论模型,实际无法实现 |
| 实际PID(带微分滤波) | 3 | 2 (一个在原点,一个在 -N) |
工程中最常用的形式 |
| 串联式PID | 2 | 1 (在原点) | 与理想并行式数学等价 |
核心要点:
- 极点 由积分项(I)引入,它决定了系统在低频段的特性(提高无静差度)。
- 零点 由比例项(P)、积分项(I)和微分项(D)共同作用产生,它们决定了控制器的动态响应速度和稳定性。
- 讨论PID的零极点时,必须明确其具体形式 。在绝大多数实际工程应用和仿真中,我们指的都是在结论2 中的实际PID控制器(带微分滤波),即 3个零点,2个极点。