文章目录
- [T1 木棍](#T1 木棍)
- [T2 巧克力](#T2 巧克力)
- [T3 龙脊雪山](#T3 龙脊雪山)
T1 木棍
题意
有 n n n 根木棒,从中选 6 6 6 根,将这 6 6 6 根拼成一个正方形,任意木棒可以接成一根新的木棒,注意木棒不能弯曲,求总方案数。 1 ≤ n ≤ 5 × 1 0 3 , 1 ≤ a i ≤ 1 0 7 1 \le n \le 5 \times 10^3,1 \le a_i \le 10^7 1≤n≤5×103,1≤ai≤107
思路
注意到这个正方形的四条边可以形如 { a , a , b + c , d + e } \{a,a,b+c,d+e\} {a,a,b+c,d+e} 或 { a , a , a , b + c + d } \{a,a,a,b+c+d\} {a,a,a,b+c+d} 这两种组合。对两种情况分开讨论。对于第二种可以先对于每个 a a a 预处理出 b + c + d = a b+c+d=a b+c+d=a 的三元组 { b , c , d } \{b,c,d\} {b,c,d} (满足 b ≤ c ≤ d b\le c \le d b≤c≤d);当然也可以枚举 d , a d,a d,a 求 b , c b,c b,c 。
反思
( n 2 ) × ( n − 2 2 ) ≠ ( n 4 ) \binom{n}{2}\times \binom{n-2}{2} \ne \binom{n}{4} (2n)×(2n−2)=(4n)
代码
cpp
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=5e3+5,maxs=1e7+5;
ll C(ll x,ll y){
if(x<y) return 0ll;
if(y==2) return x*(x-1)/2;
if(y==3) return x*(x-1)/2*(x-2)/3;
if(y==4) return x*(x-1)/2*(x-2)/3*(x-3)/4;
}
ll a[maxn],b[maxn],sum[maxn],f[maxs];
map<int,int>mp;
int main(){
freopen("stick.in","r",stdin);
freopen("stick.out","w",stdout);
int n; cin>>n; int cnt=0;
for(int i=1;i<=n;i++){
cin>>a[i];
if(!mp[a[i]]) mp[a[i]]=++cnt;
sum[mp[a[i]]]++;
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++)
b[i]=a[i];
int m=unique(b+1,b+n+1)-b-1;
ll ans=0;
for(int i=1;i<=m;i++)
if(sum[mp[b[i]]]>=2){
ll fs=0,s=0;
for(int j=i-1;j>=1;j--){
if(b[i]-b[j]>b[j]) break;
int tmp=b[i]-b[j];
if(tmp==b[j]){
if(sum[mp[tmp]]>=2){
fs+=C(sum[mp[tmp]],4);//! C(x,2)*C(x-2,2) ≠C(x,4)
fs+=s*C(sum[mp[tmp]],2);
s+=C(sum[mp[tmp]],2);
}
continue;
}
if(sum[mp[tmp]]){
if(sum[mp[b[j]]]>=2&&sum[mp[tmp]]>=2) fs+=C(sum[mp[b[j]]],2)*C(sum[mp[tmp]],2);
ll d=sum[mp[tmp]]*sum[mp[b[j]]];
fs+=s*d,s+=d;
}
}
ans+=fs*C(sum[mp[b[i]]],2);
}
for(int i=1;i<=m;i++){
for(int j=i+1;j<=m;j++)
if(sum[mp[b[j]]]>=3){
ans+=sum[mp[b[i]]]*C(sum[mp[b[j]]],3)*f[b[j]-b[i]];
if(sum[mp[b[i]]]>=2&&b[j]-2*b[i]>=0&&b[j]-2*b[i]<b[i])
ans+=C(sum[mp[b[i]]],2)*C(sum[mp[b[j]]],3)*sum[mp[b[j]-2*b[i]]];
if(sum[mp[b[i]]]>=3&&3*b[i]==b[j]) ans+=C(sum[mp[b[i]]],3)*C(sum[mp[b[j]]],3);
}
for(int j=1;j<i;j++)
if(b[i]+b[j]<=b[m]) f[b[i]+b[j]]+=sum[mp[b[i]]]*sum[mp[b[j]]];
if(b[i]+b[i]<=b[m]&&sum[mp[b[i]]]>=2) f[b[i]+b[i]]+=C(sum[mp[b[i]]],2);
}
cout<<ans;
return 0;
}T2 巧克力
link
思路
易知每个连通块的平均数等于全局平均数,考虑先让每个 a i a_i ai 减去全局平均数(由于平均数会是分数我们将对整体 × 2 n \times 2n ×2n) ,这样每个连通块的限制化简为 ( ∑ a i ) = 0 (\sum a_i) =0 (∑ai)=0 。记 s u m i , j sum_{i,j} sumi,j 表示第 i i i 行 a a a 的前缀和。若连通块在同一行,记 ( l , r ] (l,r] (l,r] ,有 s u m i , r − s u m i , l = 0 sum_{i,r}-sum_{i,l}=0 sumi,r−sumi,l=0 ;若连通块跨越两行,记连通块中每一行最右侧的位置为 r 0 , r 1 r0,r1 r0,r1 ,有 s u m 0 , r 0 + s u m 1 , r 1 = 0 sum_{0,r0}+sum_{1,r1}=0 sum0,r0+sum1,r1=0 。这样我们知道如何快速判断一个连通块是否合法。
考虑 DP 。
有一个想法,设 f i , j f_{i,j} fi,j 表示当前第 0 0 0 行考虑到第 i i i 位,第 1 1 1 行考虑到第 j j j 位且此时已经划分了的块全部合法的块数。发现有如下情况会使这个状态转移不了:
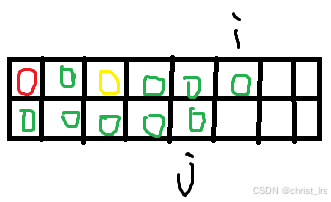
于是再次重新设状态。设 f i , j , k f_{i,j,k} fi,j,k 表示考虑到第 i i i 列, ( 0 , i ) (0,i) (0,i) 所在块和为 j j j , ( 1 , i ) (1,i) (1,i) 所在块和为 k k k 此时的块数。复杂度爆炸。考虑优化。发现如果 i , j i,j i,j 在不同的块且两个块的和均不为 0 0 0 的话状态没用,因为可以等到块和为 0 0 0 的时候再转移。重新记 f i , j f_{i,j} fi,j 表示考虑到第 i i i 列,此时第 j j j 行的 ( j , i ) (j,i) (j,i) 所在块和为 0 0 0 ,另一行不确定时分成的最多块数。答案为 m a x ( f n , 0 , f n , 1 ) max(f_{n,0},f_{n,1}) max(fn,0,fn,1) 。
分讨转移:
- 将两行的数并入同一个块中, f i , j ← m a x ( f i − 1 , 0 , f i − 1 , 1 ) f_{i,j}← max(f_{i-1,0},f_{i-1,1}) fi,j←max(fi−1,0,fi−1,1) ;
- 只在一行划分一个和为 0 0 0 的块,记块为 ( k , i ] (k,i] (k,i] ,当 s u m j , i − s u m j , k = 0 sum_{j,i}-sum_{j,k}=0 sumj,i−sumj,k=0 ,有 f i , j ← f k , j + 1 f_{i,j}←f_{k,j}+1 fi,j←fk,j+1 ;
- 划分一个横跨两行的块,记另一行在此块中最右侧的位置的左边一位为 k k k ( k < i k\lt i k<i),当 s u m j , i + s u m j ⊕ 1 , k = 0 sum_{j,i}+sum_{j\oplus 1,k}=0 sumj,i+sumj⊕1,k=0 时,有 f i , j ← f i ⊕ 1 , k + 1 f_{i,j}← f_{i\oplus 1,k}+1 fi,j←fi⊕1,k+1;
- 特殊情况:另一行不确定为 0 0 0 的部分拼上去上一行和可以为 0 0 0 时,即 s u m 0 , i + s u m 1 , i = 0 sum_{0,i}+sum_{1,i}=0 sum0,i+sum1,i=0 时, f i , j ← m a x ( f i , 0 , f i , 1 ) + 1 f_{i,j}←max(f_{i,0},f_{i,1})+1 fi,j←max(fi,0,fi,1)+1 。
这个 O ( n 3 ) O(n^3) O(n3) dp 可以通过 map 优化到 O ( n 2 ) O(n^2) O(n2) 。
代码
cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=2e5+5;
int f[maxn][2];
ll a[2][maxn],sum[2][maxn];
map<ll,int>mp[6];//mp[0(0/1)/1(0/1)][j]
int main(){
freopen("sweet.in","r",stdin);
freopen("sweet.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n; cin>>n; ll s=0;
for(int i=0;i<=1;i++)
for(int j=1;j<=n;j++){
cin>>a[i][j];
s+=a[i][j];
}
for(int i=0;i<=1;i++)
for(int j=1;j<=n;j++){
a[i][j]*=2ll*n,a[i][j]-=s;
sum[i][j]=sum[i][j-1]+a[i][j];
}
mp[0][0]=mp[1][0]=mp[2][0]=mp[3][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=1;j++){
f[i][j]=max(f[i-1][0],f[i-1][1]);
int k=(j^1);
if(mp[k].count(sum[k][i])) f[i][j]=max(f[i][j],mp[k][sum[k][i]]+1);
if(mp[k|2].count(-sum[k][i])) f[i][j]=max(f[i][j],mp[k|2][-sum[k][i]]+1);
}
if(sum[0][i]+sum[1][i]==0) f[i][0]=f[i][1]=max(f[i][0],f[i][1])+1;
for(int j=0;j<=1;j++){
mp[j][sum[j][i]]=max(mp[j][sum[j][i]],f[i][j^1]);
mp[j|2][sum[j^1][i]]=max(mp[j|2][sum[j^1][i]],f[i][j]);
}
}
cout<<max(f[n][0],f[n][1]);
return 0;
}T3 龙脊雪山
由于如果起点确定,能走的山峰是一段区间,可以用的灯笼也是一段区间,于是dp ,好像 O ( n 2 ) O(n^2) O(n2) dp 挺好想?