数据结构实战：顺序表全解析 - 从零实现到性能分析

时间醉酒2025-10-13 13:04

1.2 线性表

基础概念与结构特性

定义 ：由 n ( n >= 0 )个数据特性相同的元素构成的有限序列，称为线性表。（线性表是n个元素的有限序列，其中 n 个数据是相同数据类型的。)

分类：顺序表和链表

核心属性：

  • 长度： 线性表中实际包含的数据元素个数 n 称为线性表的长度。
  • 空表： 当长度 n=0 时，该线性表称为空表。

非空线性表的结构特征：

对于任意非空线性表，其元素序列需满足以下四个结构特性：

  1. 首元素唯一性： 必存在一个唯一的元素被称作"第一个"元素（也称首元素）。
  2. 尾元素唯一性： 必存在一个唯一的元素被称作"最后一个"元素（也称尾元素）。
  3. 前驱性： 除第一个元素外，其余所有元素都只有一个前驱（紧邻其前的元素）。
  4. 后继性： 除最后一个元素外，其余所有元素都只有一个后继（紧邻其后的元素）。

定义 ：用一组连续的内存单元依次存储线性表的各个元素，也就是说，逻辑上 相邻的元素，实际的物理存储空间 也是连续的 。（这和数组类似，在数组里**，'A 后面是 B' （这是逻辑上的前后关系），就意味着 A 的储存单元紧挨着 B 的储存单元（这是物理上的连续排列）。**

一.顺序表 - 定义和初始化以及遍历

(1)顺序表定义

cs 复制代码 
//宏定义与类型定义
#define MAXSIZE 100
typedef int ElemType; //定义 int 的别名为 ElemType （方便后续修改数据类型）

//结构体定义(SeqList)
typedef struct{
    ElemType data[MAXSIZE]; //声明了一个长度为MAXSIZE(100)的整数类型的数组
    int length; //用于记录当前顺序表中实际存储了多少个元素
}SeqList;

(2)顺序表初始化

cs 复制代码 
//初始化函数 (initList)
void initList(SeqList *L)
{
    L->length = 0;
}

通过传入结构体的指针L，将其中存储当前元素数量的 length 成员设置为 0。这使得当我们声明一个新的顺序表时，它就是空的。

cs 复制代码 
//mian函数
int main(int argc,char const *argv[])
{
    //声明一个顺序表并初始化
    SeqList list;
    initList(&list);
    printf("初始化成功，目前长度占用%d\n",list.length);
    printf("目前占用内存%zu字节\n",sizeof(list.data)); //打印数组部分占用的字节数
    return 0;
}

(3)遍历函数

cs 复制代码 
//遍历
void listElem(SeqList *L)
{
    for (int i = 0; i < L->length; i++)
    {
        printf("%d",L->data[i]);
    }
    printf("\n");
}

二.顺序表 - 尾部插入元素

cs 复制代码 
//添加元素的核心代码
int appendElem(SeqList *L,ElemType e) //传入顺序表的指针，想要添加的元素
{
    if(L->length>=MAXSIZE)
    {
        printf("顺序表已满\n");
        return 0;
    }

    // 核心逻辑：添加元素
    L->data[L->length] = e; //L->data 数组，L->length 数组的下标
    L->length++;
    return 1;
}
  • L->data 表示："找到指针 L 所指向的顺序表，并访问它的数据数组部分。"
  • L->length 表示："找到指针 L 所指向的顺序表的长度变量。"

在main函数里调用appendElem函数

cs 复制代码 
//mian函数
int main(int argc,char const *argv[])
{
    //声明一个顺序表并初始化
    SeqList list;
    initList(&list);
    printf("初始化成功，目前长度占用%d\n",list.length);
    printf("目前占用内存%zu字节\n",sizeof(list.data)); //打印数组部分占用的字节数

    //调用函数
    appendElem(&list,88);
    appendElem(&list,45);
    appendElem(&list,43);
    appendElem(&list,17);
    listElem(&list);

    return 0;
}

结果如下：

三.顺序表 - 中间插入元素

cs 复制代码 
//插入元素的核心代码
int insertElem(SeqList *L,int pos,ElemType e)
{
    if(L->length >= MAXSIZE)
    {
        printf("表已经满了\n");
        return 0;
    }

    if(pos < 1 || pos > L->length)
    {
        printf("插入位置错误\n");
        return 0;
    }

    //核心逻辑
    if (pos <= L->length)
    {
        for (int i = L->length-1; i >= pos-1; i--)
        {
            L->data[i+1] = L->data[i];
        }
        L->data[pos-1] = e;
        L->length++;
        }
        return 1;
}

在main函数里调用appendElem函数

cs 复制代码 
int main(int argc, char const* argv[])
{
    //声明一个顺序表并初始化
    SeqList list;
    initList(&list);
    printf("初始化成功，目前长度占用%d\n", list.length);
    printf("目前占用内存%zu字节\n", sizeof(list.data)); //打印数组部分占用的字节数

    appendElem(&list, 88);
    appendElem(&list, 45);
    appendElem(&list, 43);
    appendElem(&list, 17);
    listElem(&list);

    //调用函数
    insertElem(&list,2,18);
    listElem(&list);

    return 0;
}

结果如下：

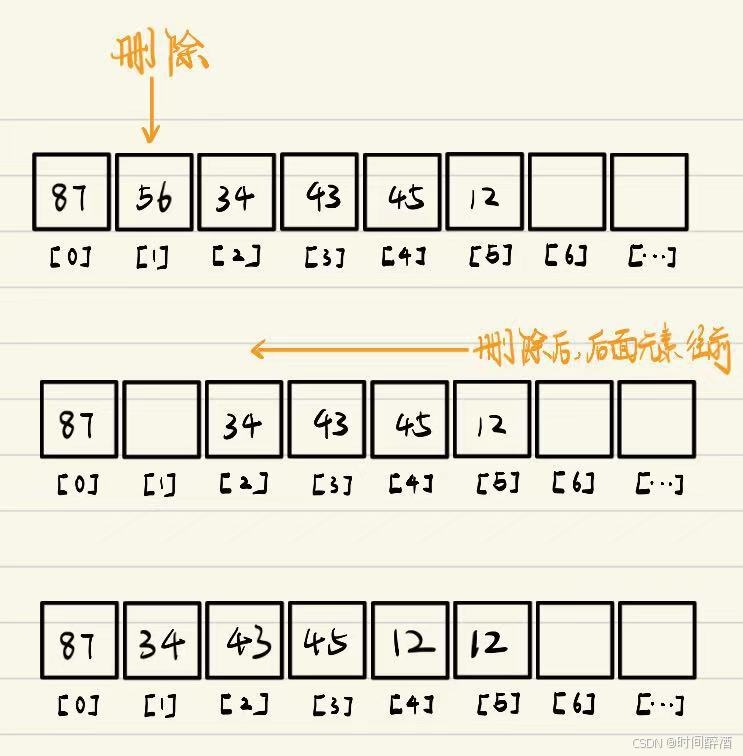
四.顺序表 - 删除元素

虽然说是删除，但本质上是覆盖的过程。

34覆盖56，43覆盖34，45覆盖43，12覆盖45，后面就没有元素覆盖12了，所以我们可以看最后顺序表中有两个12，那么我们怎么处理呢？

答案是：长度-1( L->length-- )就可以了

cs 复制代码 
//删除元素的核心逻辑
int deleteElem(SeqList* L, int pos, ElemType* e) 
{
    *e = L->data[pos - 1];  //*e用来储存被删掉数据的位置(L->data[pos-1])
    if (pos < L->length)
    {
        for (int i = pos; i < L->length; i++)
        {
            L->data[i - 1] = L->data[i];
        }
    }
    L->length--;
    return 1;

}

mian函数中调用

cs 复制代码 
//mian函数
int main(int argc, char const* argv[])
{
    //声明变量delData
    ElemType delData;
    //声明一个顺序表并初始化
    SeqList list;
    initList(&list);
    printf("初始化成功，目前长度占用%d\n", list.length);
    printf("目前占用内存%zu字节\n", sizeof(list.data)); //打印数组部分占用的字节数

    appendElem(&list, 88);
    appendElem(&list, 45);
    appendElem(&list, 43);
    appendElem(&list, 17);
    listElem(&list);

    insertElem(&list,2,18);
    listElem(&list);
    
    //调用函数
    deleteElem(&list, 2, &delData);
    printf("被删除的数据为：%d\n", delData);
    listElem(&list);

    return 0;
}

结果如下：

五.顺序表 - 查找

cs 复制代码 
//查找的核心逻辑
int findElem(SeqList* L,ElemType e)
{
    for (int i = 0; i < L->length; i++)
    {
        if (L->data[i] == e)
        {
            return i + 1;
        }
    }
    return 0;
}

mian中调用

cs 复制代码 
//mian函数
int main(int argc, char const* argv[])
{
    ElemType delData;
    //声明一个顺序表并初始化
    SeqList list;
    initList(&list);
    printf("初始化成功，目前长度占用%d\n", list.length);
    printf("目前占用内存%zu字节\n", sizeof(list.data)); //打印数组部分占用的字节数

    appendElem(&list, 88);
    appendElem(&list, 45);
    appendElem(&list, 43);
    appendElem(&list, 17);
    listElem(&list);

    insertElem(&list,2,18);
    listElem(&list);

    deleteElem(&list, 2, &delData);
    printf("被删除的数据为：%d\n", delData);
    listElem(&list);

    //调用
    printf("%d\n", findElem(&list, 43));

    return 0;
}

结果如下：

六.顺序表 - 动态分配内存地址初始化

cs 复制代码 
//动态分配内存地址初始化
typedef struct {
    ElemType* data;// 存储元素数据的指针，指向一块动态分配的内存
    int length; // 当前顺序表中元素的数量
} SeqList;

SeqList* initList(SeqList* L) 
{
    //在堆内存中开辟SeqListd结构体空间
    SeqList* L = (SeqList*)malloc(sizeof(SeqList)); 
    //在堆内存中开辟顺序表储存数据的连续空间（相当于上面的data(100)）
    L->data = (ElemType*)malloc(sizeof(ElemType) * MAXSIZE);
    //初始化长度
    L->length = 0;
    //返回指向新创建的顺序表的指针
    return L;
}

将数据从栈内存中转移到堆内存中开辟空间

分析：

SeqList* L = (SeqList*)malloc(sizeof(SeqList));

malloc函数表示在内存当中开辟一片内存空间，默认返回值是void*（通用类型数据的指针)，所以要做类型的强制转换(SeqList*)，sizeof(SeqList)表示SeqList需要的空间，用SeqList指针接返回的值（SeqList* L）

完整代码实例：

cs 复制代码 
#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100
typedef int ElemType;

// 动态分配顺序表结构体
typedef struct {
    ElemType* data;  // 存储元素数据的指针，指向一块动态分配的内存
    int length;      // 当前顺序表中元素的数量
} SeqList;

// 动态分配内存地址初始化
SeqList* initList()  // 移除参数，直接返回指针
{
    // 在堆内存中开辟SeqList结构体空间
    SeqList* L = (SeqList*)malloc(sizeof(SeqList)); 
    if (L == NULL) {
        printf("结构体内存分配失败\n");
        return NULL;
    }
    
    // 在堆内存中开辟顺序表储存数据的连续空间
    L->data = (ElemType*)malloc(sizeof(ElemType) * MAXSIZE);
    if (L->data == NULL) {
        printf("数据内存分配失败\n");
        free(L);  // 释放之前分配的结构体
        return NULL;
    }
    
    // 初始化长度
    L->length = 0;
    
    // 返回指向新创建的顺序表的指针
    return L;
}

// 销毁顺序表
void destroyList(SeqList* L) {
    if (L != NULL) {
        if (L->data != NULL) {
            free(L->data);  // 先释放数据数组
        }
        free(L);  // 再释放结构体
    }
}

// 遍历函数
void listElem(SeqList* L) {
    if (L->length == 0) {
        printf("顺序表为空\n");
        return;
    }
    printf("顺序表元素：");
    for (int i = 0; i < L->length; i++) {
        printf("%d ", L->data[i]);
    }
    printf("\n");
}

// 尾部插入元素
int appendElem(SeqList* L, ElemType e) {
    if (L->length >= MAXSIZE) {
        printf("顺序表已满\n");
        return 0;
    }
    L->data[L->length] = e;
    L->length++;
    return 1;
}

// 主函数测试
int main() {
    // 创建顺序表
    SeqList* list = initList();
    if (list == NULL) {
        printf("顺序表初始化失败\n");
        return -1;
    }
    printf("顺序表初始化成功，当前长度：%d\n", list->length);
    
    // 添加元素
    appendElem(list, 10);
    appendElem(list, 20);
    appendElem(list, 30);
    appendElem(list, 40);
    
    // 遍历显示
    listElem(list);
    printf("当前长度：%d\n", list->length);
    
    // 销毁，避免内存泄漏
    destroyList(list);
    
    return 0;
}

顺序表的核心概念总结

基于数组 (Array-based) ：数据存储在一个固定大小的数组中，这保证了物理存储是连续的。

随机访问 (Random Access) ：正因为物理地址连续，我们可以通过索引（L->data[i]）高效地访问任何一个元素，时间复杂度为 O(1)。

插入和删除效率低 ：appendElem（即在表尾添加）是高效的 O(1)操作（只要没满），但如果在表头或中间 插入/删除元素，需要将后面所有元素整体移动，时间复杂度是 O(n)。

但缺点是：

容量固定 ：一旦定义了 MAXSIZE，此表的最大容量就是固定的。当 length == MAXSIZE 时，表满。

插入/删除效率低：平均需要移动半个表，时间复杂度O(n)。

  • 插入时的"多米诺效应"：在位置i插入新元素，需要将i之后的所有元素都向后移动一位

  • 删除时的"补位操作"：删除位置i的元素，需要将i之后的所有元素都向前移动一位

那么，有没有一种数据结构，既能保持线性表"逻辑上相邻"的特性，又能在物理存储上摆脱连续性的束缚，从而解决插入删除的效率问题呢？

答案是肯定的------这就是我们接下来要重点学习的链表(Linked List)。

敬请期待下一篇：《数据结构实战（二）链表：打破存储连续性的高效线性表》

相关推荐
Craaaayon3 小时前
【数据结构】二叉树-图解广度优先搜索
java·数据结构·后端·算法·宽度优先
刘某某.4 小时前
数组和小于等于k的最长子数组长度b
java·数据结构·算法
chenyuhao20244 小时前
《C++二叉引擎：STL风格搜索树实现与算法优化》
开发语言·数据结构·c++·后端·算法
杂亿稿4 小时前
优先级队列
数据结构
要争气5 小时前
5 二分查找算法应用
java·数据结构·算法
欧阳x天5 小时前
堆(超详解)
数据结构
vir026 小时前
翻转后1的数量(dp)
java·数据结构·算法
艾莉丝努力练剑7 小时前
【C++STL ：list类 (二) 】list vs vector：终极对决与迭代器深度解析 && 揭秘list迭代器的陷阱与精髓
linux·开发语言·数据结构·c++·list
游坦之7 小时前
基于Java Swing的智能数据结构可视化系统 | 支持自然语言交互的AI算法助手
java·数据结构·交互
热门推荐
01BongoCat - 跨平台键盘猫动画工具02两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答03智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践042025羊城杯网络安全大赛 wp05GitHub 镜像站点06UV安装并设置国内源07Linux下V2Ray安装配置指南08Spring Boot 实现微信登录，So Easy !095大DOM/BOM核心考点：从入门到精通，让面试官眼前一亮10Cursor Plan Mode：AI 终于知道先想后做了