代码随想录刷题——二叉树篇（十三）

cpp 复制代码

class Solution{
public:
	TreeNode* traversal(vector<int>& inorder,vector<int> postorder){
		if(postorder.size()==0) return NULL;
		int rootValue = postorder.back();
		TreeNode* root = new TreeNode(rootValue);
		if(postorder.size()==1) return root;
		int i;
		for(i=0;i<inorder.size();i++){
			if(inorder[i]==rootValue) break;
		}
		vector<int> leftInorder(inorder.begin(),inorder.begin()+i);
		vector<int> rightInorder(inorder.begin()+i+1,inorder.end());
		postorder.pop_back();
		vector<int> leftPostorder(postorder.begin(),postorder.begin()+leftInorder.size());
		vector<int> rightPostorder(postorder.begin()+leftInorder.size(),postorder.end());
		root->left = traversal(leftInorder,leftPostorder);
		root->right = traversal(rightInorder,rightPostorder);
		return root;
	}
	TreeNode* buildTree(vector<int>& inorder,vector<int> postorder){
		if(inorder.size()==0||postorder.size()==0) return NULL;
		return traversal(inorder,postorder);
	}
};

递归法（下标版本）：

cpp 复制代码

class Solution{
public:
	TreeNode* traversal(vector<int>& inorder,vector<int>& postorder,int inbegin,int inend,int postbegin,int postend){
		if(postbegin==psotend) return NULL;
		int rootValue=postorder[postend-1];
		TreeNode* root=new TreeNode(rootValue);
		if(postend-postbegin==1) return root;
		int i;
		for(i=inbegin;i<inend;i++){
			if(inorder[i]==rootValue) break;
		} 
		int linbegin = inbegin;
		int linend = i; 
		int rinbegin = i+1;
		int rinend = inend;
		
		int lpostbegin = postbegin;
		int lpostend = postbegin + i - inbegin;
		int rpostbegin = postbegin + i - inbegin;
		int rpostend = postend - 1;
		root->left = traversal(inorder,postorder,linbegin,linend,lpostbegin,lpostend);
		root->right = traversal(inorder,postorder,rinbegin,rinend,rpostbegin,rpostend);
		return root;
	}
	TreeNode* buildTree(vector<int> inorder,vector<int> postorder){
		if(inorder.size()==0||postorder.size()==0) return NULL;
		return traversal(inorder,postorder,0,inorder.size(),0,postorder.size());
	}
};

105. 从前序与中序遍历序列构造二叉树
递归法（下标版本）：

cpp 复制代码

class Solution{
public:
	TreeNode* traversal(vector<int>& preorder,vector<int>& inorder,int inbegin,int inend,int prebegin,int preend){
		if(prebegin==preend) return NULL;
		TreeNode* root = new TreeNode(preorder[prebegin]);
		if(preend-prebegin==1) return root;
		int i;
		for(i=inbegin;i<inend;i++){
			if(inorder[i]==preorder[prebegin]) break;
		}
		int linbegin=inbegin;
		int linend=i;
		prebegin++;
		int lprebegin=prebegin;
		int lpreend=prebegin+i-inbegin;
		
		int rinbegin=i+1;
		int rinend=inend;
		int rprebegin=prebegin+i-inbegin;
		int rpreend=preend;
		root->left=traversal(preorder,inorder,linbegin,linend,lprebegin,lpreend);
		root->right=traversal(preorder,inorder,rinbegin,rinend,rprebegin,rpreend);
		return root;
	}
	TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0||inorder.size()==0) return NULL;
        return traversal(preorder,inorder,0,preorder.size(),0,inorder.size());
    }
};

其他：

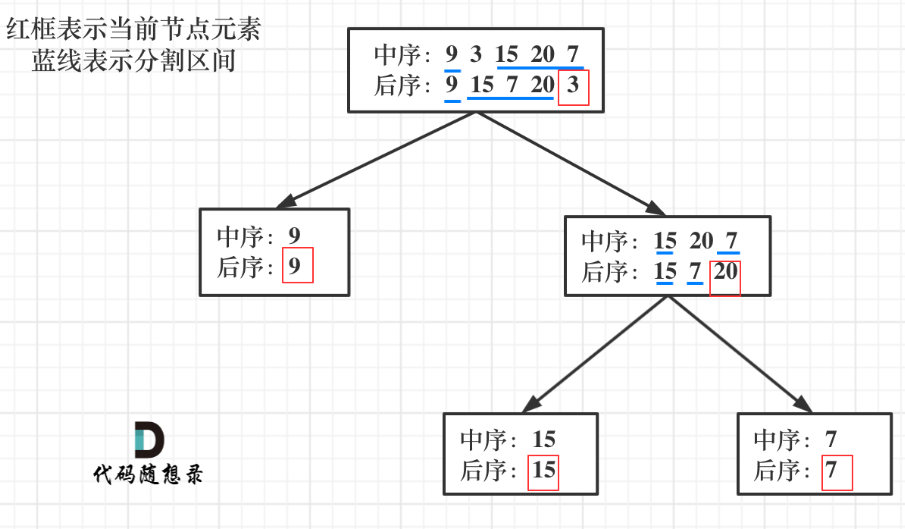
（1）先找根节点：后序遍历 的最后一个 ，然后用后序遍历的节点切中序遍历 ，再根据中序遍历切开的左右子数组切后序遍历。

这张图画的太好了：

vector的一些操作：back()、find()、resize()、pop_back()

（2）vector<int> vec(inorder.begin(),inorder.begin()+num)这种构建方式，num=0时会构建一个空的vector，构造时可以按意义理解：vec(i，j) ，则取**[ i , j )** ，左闭右开 ，迭代器可以理解成指向一个位置的指针，加几移动几个位置

（3）这道题的递归法其实和之前的思路一样，只不过是把inorder 和postorder 这两个遍历数组的不同情况 和节点所处的位置类型进行了对应：

a.inorder和postorder为空 ------------------------>到了空节点

b.inorder和postorder的size为1 ----------------->到了叶子节点

c.其他（递归函数的其他区域）---------------->其他节点 的处理逻辑

和三部曲基本一致，先确定参数（中序和后序数组），再确定终止处理条件 （到空节点和叶子节点（这里之所以是两个情况，是因为存在某个节点只有一个子节点的情况）），最后确定其他节点的处理逻辑（切分数组、递归）

下标版也是一样：

a.postbegin**==** postend----------------------------->到了空节点

b.postend**-** postbegin**==0** --------------------------->到了叶子节点

c.其他（递归函数的其他区域）------------------>其他节点 的处理逻辑

（4）下标版本同样需要保持左闭右开 的状态，下标左为闭区间 ，右为开区间

（5）105题一开始traversal函数的vector<int>参数忘记写引用了，执行用时和消耗内存都差了很多，原因是不加引用的话，每次递归都会把vector<int>参数复制一遍

（6）中序+前序/后序数组可以构建二叉树，只有前序和后序不行