超详细链式插补 (MICE) 多元插补：机器学习模型的高级缺失数据处理

多元链式方程插补（MICE）是一个强大的框架，用于填补缺失值，同时最大限度地减少插补过程中的偏差和不确定性。

然而，理解和利用MICE具有挑战性，因为其迭代的、依赖于模型的特性使其过程变得复杂。

在本文中，我将通过实际示例探讨其核心机制，例如使用PMM和LR等方法的MICE，并与一个标准的基于模型的插补方法作为基线进行比较。

什么是多元链式方程插补（MICE）？

多元链式方程插补（MICE）是一种插补方法，即用估计值填充缺失数据点的技术。

主要的插补方法分为三类：

统计方法：均值、中位数、众数插补等。
基于模型的方法：KNN插补、回归插补、GAIN（生成对抗插补网络）等。
时间序列特定方法：前向/后向填充。

MICE被归类为基于模型的方法，尽管它通过迭代使用预测模型来预测缺失值，采取了更复杂的方法。

下图展示了整个过程：

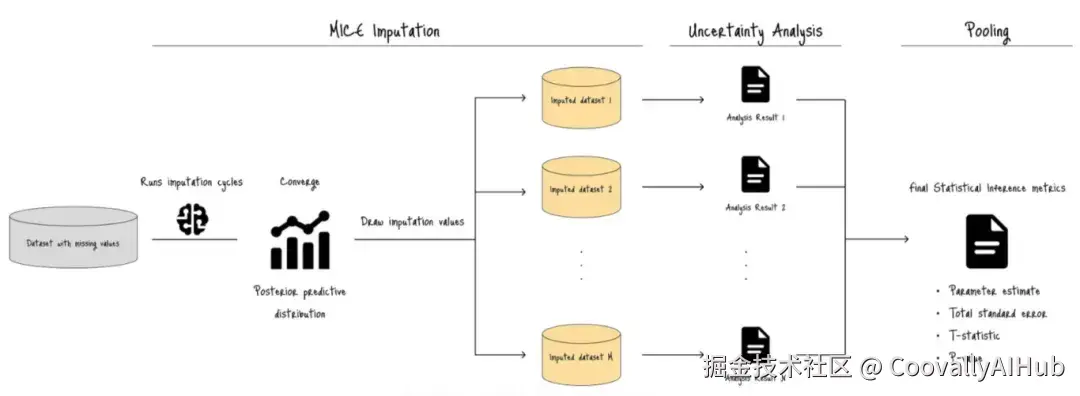
添加图片注释，不超过 140 字（可选）

MICE首先使用预测模型运行插补循环，生成带有缺失值的目标变量的后验分布。

然后，它通过迭代过程（图A中的M次）从该分布中抽取插补值。

这个过程生成了多个具有唯一插补值的插补数据集（黄色标注的插补数据集1, 2, ..., M）。

最后，进行不确定性分析和合并，生成一组最终的统计推断指标，包括合并后的参数估计、总标准误、t统计量和p值。

这些指标衡量了由缺失值引入的不确定性，并检查插补数据集在统计上是否足以执行可靠的后续推断。

核心概念

在插补循环期间，MICE涉及一个链式预测结构，其中预测模型按顺序插补缺失值，并利用之前的插补结果。

例如，假设我们有一个简单的数据集，包含两个特征：Income（X1）和Age（X2），且存在缺失值：

添加图片注释，不超过 140 字（可选）

标准的回归插补，例如，通过简单地应用学习到的近似函数来填充缺失值：

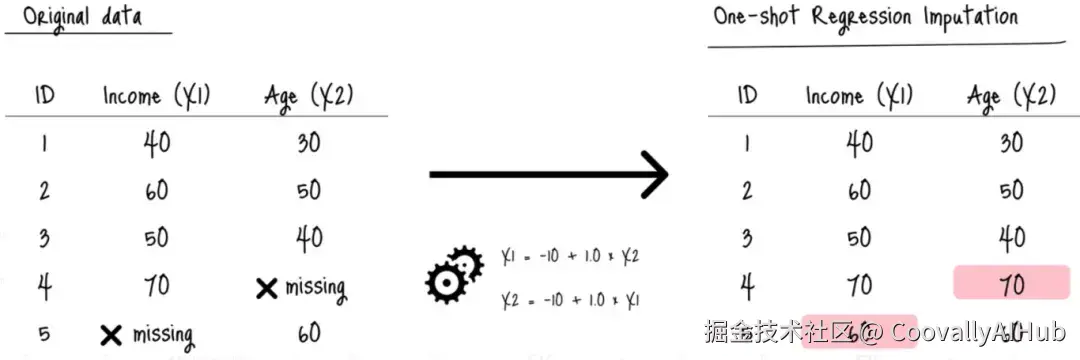
添加图片注释，不超过 140 字（可选）

这种方法本身没有错。

但由于回归模型是在数据的一个小的、不完整的部分上训练的，插补值（粉色单元格）可能存在偏差。

相比之下，MICE算法利用了链式预测：

添加图片注释，不超过 140 字（可选）

首先，MICE用初始猜测值（如均值，浅粉色单元格）替换所有缺失值。

然后，它使用所有数据（包括新插补的值，如X1中的"57"）来持续优化插补值（深粉色单元格）。

MICE重复此过程数次，直到插补值稳定，表明已收敛。

随机缺失（MAR）假设

由于其链式预测的性质，MICE在强随机缺失（MAR）假设下运行，即某个值缺失的可能性仅取决于数据集中已存在的值。

当缺失机制被分类时：

完全随机缺失（MCAR）：缺失值是纯粹随机的。
非随机缺失（MNAR）：缺失值取决于缺失列中值的特定范围（例如，家庭收入高的调查受访者在调查中跳过回答家庭收入问题。此时，家庭收入的缺失取决于实际的家庭收入值）。

对于MCAR和MNAR，更有可能使用其他插补方法：

对于MCAR：除MICE外的统计方法、基于模型的方法。
对于MNAR：特别是针对复杂数据集的自动编码器，领域特定模型。

何时使用MICE

MICE在MAR情况下效果最佳，因为它可以：

实现高精度：与其他一次性插补方法相比，迭代过程提供了有效的不确定性估计。
处理多元依赖关系：比简单的非迭代插补方法能更好地建模多元依赖关系。
通过利用其他变量创建现实的插补值来避免插补值偏差。

然而，它也有局限性，例如：

与其他插补方法相比，计算过程较慢。
迭代过程引入复杂性。
依赖于底层模型假设：MICE框架中模型的线性等底层假设会影响插补值的准确性。

因此，选择能最大化其优势的场景至关重要。

这些场景包括：

多元缺失数据：如其名所示，缺失值分散在多个变量中且彼此相关的数据集可以利用MICE的链式预测特性。
混合变量类型：包含连续和分类变量且存在缺失值的数据集。
高缺失率：缺失值占整个样本的比例足够高，达到约10%或更多，此时其他插补方法可能会引入严重偏差。

实际上，像临床试验和公共卫生调查这类需要无偏参数估计的研究，是MICE在现实世界中的绝佳应用案例。

在下一节中，我将详细探讨MICE算法的工作原理。

MICE算法工作原理

如图A所示，插补过程包括以下步骤：

使用占位值进行初始插补。
建模后验分布并从中抽取样本。
重复步骤2直到收敛。
重复步骤3以生成具有唯一插补值的多个数据集。
进行不确定性分析和合并。

让我们详细看看。

步骤 1. 初始插补

第一步是对所有缺失值执行简单的插补，例如均值或中位数插补。

为了概括该过程：

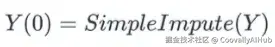
添加图片注释，不超过 140 字（可选）

其中 Y 是一个包含 P 个变量的数据集，Y = [Y_1, Y_2, ..., Y_P]，Y(t) 表示在插补周期 t 时的数据集 Y。

在插补之前，Y 包含观测值（无缺失值的标记值）和缺失值。

步骤 2. 后验分布与抽样

下一步是对后验分布进行建模并从中抽取样本。

该过程首先：

训练预测模型，
对目标变量的（条件）后验分布进行建模，以及
从该分布中抽取一个样本。

目标变量（如前例中的X1）包含缺失值。

这个过程用目标变量的列索引 j 和插补周期 t 来概括：

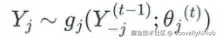
添加图片注释，不超过 140 字（可选）

其中：

Y_j：目标变量的观测值，
Y_j^(t-1)：来自前一个插补周期 t-1 的插补数据集，
g_j：由预测模型生成的后验分布，
θ_j(t)：当前插补周期 t 时预测模型的可学习参数。

这里，后验分布 g_j 随预测模型的选择而变化。

对于回归任务，主要选项有：

正态（贝叶斯）线性回归：

回归任务的基础方法
从正态分布中抽取缺失值：

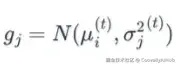
添加图片注释，不超过 140 字（可选）

其中均值 μ_i^(t) 是预测值，方差 σ_j^2(t) 是从贝叶斯框架导出的残差方差。

带自助法的正态线性回归：

g_j 与正态线性回归相同。
模型参数是从 Y 的观测数据的自助样本中估计的。

预测均值匹配（PMM）：

使用标准参数模型（如线性回归）生成预测均值。
然后，从供体池 Di（预测均值与预测均值距离最小的观测数据集）中随机抽取一个样本：

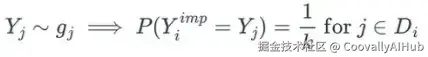
添加图片注释，不超过 140 字（可选）

其中 k 是供体池大小。其概念类似于 K 近邻。

对于分类任务，主要选项有：

正态（贝叶斯）逻辑回归：

二分类任务的基础方法。
从伯努利分布中抽取样本：

添加图片注释，不超过 140 字（可选）

其中 p_i 是第 i 个缺失值在插补周期 t 时属于类别 1 的条件概率。

多项式逻辑回归：

多项分类任务的基础方法。
从多项分布中抽取样本：

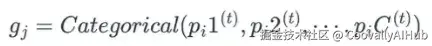
添加图片注释，不超过 140 字（可选）

其中 p_i 是第 i 个缺失值属于总 C 个类别中第 k 个类别的条件概率。

比例优势逻辑回归：

与其他方法相同，从伯努利或多项分布中抽取样本。
利用比例优势假设。
模型参数明显少于其他方法，因为跨所有累积分界点估计一组斜率系数。

步骤 3. 迭代收敛

现在，MICE算法按顺序对所有缺失变量重复步骤2，直到所有插补值收敛。

例如，如果数据集 Y 有四个具有缺失值的目标变量（例如，列索引 j = 0, 1, 2, 3），MICE 按顺序重复以下过程：

为第一个变量 j = 0 生成后验分布，
抽取样本进行插补，
移动到下一个变量 j = 1，依此类推。

这种顺序插补确保了链式预测，即在插补当前变量（例如 j = 1）时，会纳入当前已完成插补变量（例如 j = 0）的插补值。

步骤 4. 迭代------生成多个数据集

然后，MICE 将步骤 3 的整个循环重复多次（例如 20 次），以创建多个插补数据集，每个数据集具有不同的插补值。

在每个循环中，MICE 使用从后验分布 g_j 中随机抽取的值，确保数据集之间的变异性和适当的不确定性估计。

步骤 5. 不确定性分析与合并

最后一步是对所有插补数据集进行不确定性分析，并通过合并得出它们的统计推断指标。

不确定性分析

具体的分析完全取决于任务和数据类型。

但这里的一般原则是在所有插补数据集上运行完全相同的统计程序。

例如：

任务：确定年龄和BMI对胆固醇水平的影响。
MICE使用的分析模型：标准普通最小二乘（OLS）线性回归。
概念模型公式：Cholesterol ∼ β_0 + β_1⋅Age + β_2⋅BMI + ϵ
第 m 个插补数据集 D(m) 的分析结果：一组系数估计值：θ^_m = (β^_0, β^_1, β^_2) 系数的方差-协方差矩阵：U_m。

另一个例子：

任务：根据患者特征预测慢性病的可能性。
MICE使用的分析模型：二元逻辑回归。
概念模型公式：log(P(DM=1)/(1−P(DM=1))) ∼ α + γ_1⋅Age + γ_2⋅Gender + γ_3⋅Smoking
第 m 个插补数据集 D(m) 的分析结果：一组对数几率比估计值：θ^_m = (α^, γ^_1, γ^_2, γ^_3) 方差-协方差矩阵：U_m。

使用 Rubin 规则进行合并

在分析了所有插补数据集（共 M 个）之后，有 M 个模型参数估计值 (θ^_1, θ^_2, ..., θ^_M) 和方差 (U_1, U_2, ..., U_M)。

在合并过程中，Rubin 规则将这些结果组合成一个单一的估计值，以反映插补过程的整体发现。

例如，模型参数 θ 作为 M 个估计值平均后的期望值给出：

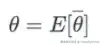
添加图片注释，不超过 140 字（可选）

其中 θˉ 是 M 个估计值的平均值（称为合并点估计）。

Rubin 规则量化了最终结果 θ 与合并点估计 θˉ 之间的估计误差（差异）：

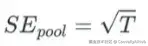
添加图片注释，不超过 140 字（可选）

其中：

SE_pool 是称为合并标准误（SE）的估计误差，
T 是总方差，汇总了组内和组间插补方差：

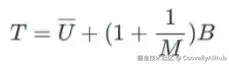
添加图片注释，不超过 140 字（可选）

其中：

Uˉ：组内插补方差，即 M 个标准误平方的平均值，量化了来自抽样变异性的不确定性。
B：组间插补方差，即 M 个估计值的样本方差，量化了由插补缺失值引入的额外不确定性。
M：插补数据集的总数。

通过使用该误差和适当的自由度，该过程可以为最终模型构建有效的置信区间和 p 值。

实际实现

在本节中，我将通过使用合成数据集训练回归任务模型来演示 MICE 的应用。

步骤包括：

结构化缺失值，
分析缺失值（统计类型），
定义插补器，
插补，
不确定性分析和合并，
模型训练和评估。

为了进行实验，我将比较以下插补方法：

MICE with PMM
MICE with 正态线性回归
标准回归插补（作为基线）

合成数据集包含 10,000 个样本（包括缺失值），具有三个特征：X1、X2 和 Y。

步骤 1. 结构化缺失值

我首先将所有的缺失值替换为 NumPy 的 np.nan。

默认情况下，Pandas DataFrame 不识别非结构化的缺失值，例如空格或像 "NA" 或 "?" 这样的文本输入。

如果未结构化，这些值会被 Pandas 视为有效条目，从而扭曲分析。

ini 复制代码

import pandas as pd
import numpy as np
def structure_missing_values(df: pd.DataFrame, target_cols: list = []) -> pd.DataFrame:
    target_cols = target_cols if target_cols else df.columns.tolist()
    # 列出非结构化缺失值选项
    unstructured_missing_vals = ['', '?', ' ', 'nan', 'N/A', None, 'na', 'None', 'none']
    # 结构化
    structured_nan = { item: np.nan for item in unstructured_missing_vals }
    structured_df = df.copy()
    for col in target_cols:
        structured_df[col].replace(structured_nan, inplace=True)
    return structured_df
df_structured = structure_missing_values(df=original_df)

步骤 2. 分析缺失值

接下来，我将分析缺失值以评估 MICE 是否适用。

我们已经了解到存在多种条件，MICE 在这些条件下效果最佳。

为了演示，我将重点对缺失值的统计类型进行分类：

ini 复制代码

from scipy import stats
def assess_missingness_diagnostics(df, target_variable='X1', missingness_type='mcar'):
    # 创建缺失指示器
    df_temp = df.copy()
    df_temp['is_missing'] = df_temp[target_variable].isna().astype(int)
    observed_vars = [col for col in df_temp.columns if col not in [target_variable, 'is_missing']]

    # 比较 1) group_observed (x1 被观测到) 和 2) group_missing (x1 缺失) 两组之间观测变量 (x2, y) 的均值
    for var in observed_vars:
        # 创建分组
        group_observed = df_temp[df_temp['is_missing'] == 0][var]
        group_missing = df_temp[df_temp['is_missing'] == 1][var]

        # 检查两组中是否有足够的样本
        if len(group_missing) < 2 or len(group_observed) < 2:
            continue
        # 执行双样本 t 检验以计算均值差异
        _, p_value = stats.ttest_ind(group_observed.dropna(), group_missing.dropna())
        mean_obs = group_observed.mean()
        mean_miss = group_missing.mean()

        # 拒绝 h0（均值相等）表明缺失机制依赖于观测变量
        if p_value < 0.05:
            print(f"  -> 结论: MAR 或 MNAR，因为均值在统计上显著不同。")
        else:
            # 未能拒绝 h0 表明独立性
            print(f"  -> 结论: MCAR，因为均值在统计上没有显著不同。")
assess_missingness_diagnostics(
    df=df_structured,
    target_variable='X1', 
    missingness_type='mar'
)

输出：

makefile 复制代码

变量: X2
均值 (X1 被观测到): 50.8368932981
均值 (X1 缺失): 38.2861376084
p值: 0.0000000000
  -> 结论: MAR 或 MNAR，因为均值在统计上显著不同。
变量: Y
均值 (X1 被观测到): -2.3461196877
均值 (X1 缺失): 8.5763595796
p值: 0.0000000000
  -> 结论: MAR 或 MNAR，因为均值在统计上显著不同。

实际上，这些统计类型可能很模糊，或者单个数据集中可能包含混合类型。

一个好的策略是使用几种不同的插补方法训练模型，然后比较它们对模型泛化能力的影响。

步骤 3. 定义插补器

在确保 MICE 适用之后，我将使用 Scikit-learn 库中的 IterativeImputer 类来定义插补器：

MICE with PMM

ini 复制代码

from sklearn.impute import IterativeImputer
imputer_mice_pmm = IterativeImputer(
    estimator=PMM(),            # pmm
    max_iter=10,                # 循环次数
    initial_strategy='mean',    # 初始插补值
    random_state=42,            # 为了可重现性
)

对于估计器，我将自定义继承 BaseEstimator 类的 PMM 类：

python 复制代码

import numpy as np
from sklearn.linear_model import LinearRegression 
from sklearn.base import BaseEstimator, RegressorMixin
# 实现一个自定义的 pmm 估计器
class PMM(BaseEstimator, RegressorMixin):
    def __init__(self, k: int = 5, base_estimator=LinearRegression()):
        self.k = k # k-近邻
        self.base_estimator = base_estimator

    def fit(self, observed_X, observed_y):
        self.base_estimator.fit(observed_X, observed_y) 

        # 存储观测数据
        self.X_donors = observed_X.copy()
        self.y_donors = observed_y.copy()

        # 预测所有观测供体的均值
        self.y_pred_donors = self.base_estimator.predict(self.X_donors) 
        return self
    # pmm 核心逻辑：从观测数据的 k 个最近邻中抽样值。x 包含缺失值
    def predict(self, X):
        # 预测缺失数据（受者）的均值
        y_pred_recipients = self.base_estimator.predict(X)
        imputed_values = np.zeros(X.shape[0])

        # 对每个受者（x 中的每一行）执行 pmm
        for i, pred_recipient in enumerate(y_pred_recipients):
            # 计算受者预测均值与所有供体预测均值之间的绝对差。
            diffs = np.abs(self.y_pred_donors - pred_recipient)

            # 获取对应 k 个最小差异（k 个最近匹配）的索引
            nearest_indices = np.argsort(diffs)[:self.k] # 取 k 个索引，避免从上一轮抽到完全相同的插补值

            # 从 k 个最近邻（供体池）中随机抽取一个观测值
            donor_pool = self.y_donors[nearest_indices]
            imputed_value = np.random.choice(donor_pool, size=1)[0]
            imputed_values[i] = imputed_value
        return imputed_values
    ## 用于 IterativeImputer 兼容性的函数
    def _predict_with_uncertainty(self, X, return_std=False):
        if return_std:
            return self.predict(X), np.zeros(X.shape[0])  # pmm 是半参数方法。设置标准差 = 0
        return self.predict(X)

库中的 KNeighborsRegressor 类可以执行类似的操作。

MICE with 正态线性回归

对于正态线性回归，我将使用库中的 BayesianRidge 模型，以确保生成唯一的插补值：

ini 复制代码

from sklearn.impute import IterativeImputer
from sklearn.linear_model import BayesianRidge
imputer_mice_lr = IterativeImputer(
    estimator=BayesianRidge(max_iter=500, tol=1e-3, alpha_1=1e-10, alpha_2=1e-10, lambda_1=1e-10, lambda_2=1e-10),
    max_iter=10,
    initial_strategy='mean',
    random_state=42,
    sample_posterior=True # 向预测添加从后验分布抽取的随机噪声。
)

步骤 4. 插补

插补过程涉及将链式预测迭代 M = 5 次。

我将定义 run_mice_imputation 函数：

python 复制代码

import pandas as pd
from sklearn.impute import IterativeImputer
def run_mice_imputation(df: pd.DataFrame, imputer: IterativeImputer, M: int = 5) -> list:
    # 迭代
    imputed_datasets= [] # 稍后用于分析和合并
    imputed_values_x1 = {}
    missing_indices_x1 = df[df['X1'].isna()].head(3).index.tolist()
    for m in range(M): 
        # 为每次迭代设置插补器（唯一的随机种子控制 pmm 抽样的 numpy 种子）
        setattr(imputer, 'random_state', m)
        # 插补 df 并将生成的数组转换为 pandas df
        df_m = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
        # 记录
        imputed_datasets.append(df_m)
        imputed_values_x1[m] = df_m['X1'].loc[missing_indices_x1].tolist()
    # 输出 - 唯一的插补值
    print("跨 M 个数据集的插补值（真正的 PMM - 期望变异性）：")
    for m_idx in range(M):
        print(f"插补数据集 {m_idx+1} - X1 的前三个插补值: {[f'{x:.14f}' for x in imputed_values_x1[m_idx]]}")
    return imputed_datasets

MICE with PMM

ini 复制代码

imputed_datasets_mice_pmm = run_mice_imputation(df=df_structured, imputer=imputer_mice_pmm, M=5)

五个已完成的数据集（D's）为目标变量 X1 生成了唯一的插补值：

跨 M 个数据集的插补值（真正的 PMM - 期望变异性）：

插补数据集 1 - X1 的前三个插补值: ['9.24212539359209', '8.86784044761337', '16.27959379662983']
插补数据集 2 - X1 的前三个插补值: ['10.67728456933526', '6.72710070935441', '8.84037515230672']
插补数据集 3 - X1 的前三个插补值: ['10.15359370564326', '6.72710070935441', '18.59563606925789']
插补数据集 4 - X1 的前三个插补值: ['10.78202129747172', '6.72710070935441', '8.84037515230672']
插补数据集 5 - X1 的前三个插补值: ['9.35638700644611', '5.15233963776858', '13.88818918534419']

MICE with 正态线性回归

ini 复制代码

imputed_datasets_mice_lr = run_mice_imputation(df=df_structured, imputer=imputer_mice_lr, M=5)

五个已完成的数据集（D's）为目标变量 X1 生成了唯一的插补值：

跨 M 个数据集的插补值（真正的 PMM - 期望变异性）：

插补数据集 1 - X1 的前三个插补值: ['12.21062281693754', '9.96558458658052', '12.49501000922409']
插补数据集 2 - X1 的前三个插补值: ['8.71573023588752', '10.85416071007341', '12.35300502646557']
插补数据集 3 - X1 的前三个插补值: ['12.72459653377737', '8.71106811173562', '11.99063594937416']
插补数据集 4 - X1 的前三个插补值: ['9.73654929041454', '3.72657966114651', '12.08960122126962']
插补数据集 5 - X1 的前三个插补值: ['8.59526280022813', '12.78831127091796', '12.39797242039489']

步骤 5. 不确定性分析与合并

创建了五个数据集后，我将运行不确定性分析和合并：

python 复制代码

import numpy as np
import statsmodels.formula.api as smf
from scipy.stats import t
def perform_analysis_and_pooling(imputed_datasets, target_param='X1'):
    m = len(imputed_datasets)
    estimates = []  # theta_m
    variances = []  # 组内插补方差 u_m
    # 1. 分析 - 在每个插补数据集上运行模型
    for i, df_m in enumerate(imputed_datasets):
        # ols 模型
        model = smf.ols(formula='Y ~ X1 + X2', data=df_m).fit()
        # 提取目标参数的估计值 (theta_m) 及其方差 (u_m)
        estimate = model.params[target_param]
        variance = model.bse[target_param]**2

        estimates.append(estimate)
        variances.append(variance)
    # 2. 使用 Rubin 规则进行合并
    # 合并点估计 (theta_bar)
    theta_bar = np.mean(estimates)

    # 组内插补方差 (u_bar)
    u_bar = np.mean(variances)

    # 组间插补方差 (b)
    b = (1 / (m - 1)) * np.sum([(est - theta_bar)**2 for est in estimates])

    # 总方差 (t)
    t_total = u_bar + (1 + (1 / m)) * b

    # 总标准误 (se)
    se_pooled = np.sqrt(t_total)

    # 方差的相对增加量 (riv) 和自由度 (v)
    riv = ((1 + (1 / m)) * b) / u_bar
    v_approx = (m - 1) * (1 + (1 / riv))**2 

    # 置信区间
    t_critical = t.ppf(0.975, df=v_approx)
    ci_lower = theta_bar - t_critical * se_pooled
    ci_upper = theta_bar + t_critical * se_pooled
    print("\n--- 使用 Rubin 规则的合并结果 ---")
    print(f"合并估计 ({target_param}): {theta_bar:.10f}")
    print(f"组内方差 (u_bar): {u_bar:.10f}")
    print(f"组间方差 (b): {b:.10f}")
    print(f"总方差 (t): {t_total:.10f}")
    print(f"合并标准误: {se_pooled:.10f}")
    print(f"方差的相对增加量 (riv): {riv:.10f}")
    print(f"自由度 (近似): {v_approx:.2f}")
    print(f"95% 置信区间: [{ci_lower:.10f}, {ci_upper:.10f}]")

    return theta_bar, se_pooled, t_total, v_approx

MICE with PMM

X1 的最终系数估计值为 2.021，95% 置信区间为 [1.954, 2.087]。

由插补过程引入的不确定性（RIV）较低（RIV ≈ 5.7%）。

合并结果：

合并估计 (X1): 2.0207316250
组内方差 (u_bar): 0.0010799139
组间方差 (b): 0.0000517265
总方差 (t): 0.0011419857
合并标准误: 0.0337932796
方差的相对增加量 (riv): 0.0574785271
自由度 (近似): 1353.92
95% 置信区间: [1.9544387504, 2.0870244996]

MICE with 正态线性回归

X1 的最终系数估计值为 2.029，95% 置信区间为 [1.963, 2.096]。

由于缺失数据引起的不确定性相对较小（RIV ≈ 6.8%）。

合并结果：

合并估计 (X1): 2.0294741750
组内方差 (u_bar): 0.0010822802
组间方差 (b): 0.0000609310
总方差 (t): 0.0011553976
合并标准误: 0.0339911402
方差的相对增加量 (riv): 0.0675586403
自由度 (近似): 998.81
95% 置信区间: [1.9627719357, 2.0961764143]

可以安全地说，在这两种方法中，由插补过程引入的不确定性是可以接受的。

步骤 6. 模型训练与评估

最后，我将在每个插补数据集上训练支持向量回归器（SVR），并平均结果以评估其泛化能力：

ini 复制代码

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error
mse_train_mice_pmm_list = []
mse_val_mice_pmm_list = []
for i, df in enumerate(imputed_datasets_mice_pmm): # 对于 PMM，使用 imputed_datasets_mice_lr 对于 LR
    # 创建 X, y
    y = df['Y']
    X = df[['X1', 'X2']]

    # 创建训练、验证、测试数据集
    test_size, random_state = 1000, 42
    X_tv, X_test, y_tv, y_test = train_test_split(X, y, test_size=test_size, shuffle=True, random_state=random_state)
    X_train, X_val, y_train, y_val = train_test_split(X_tv, y_tv, test_size=test_size, shuffle=True, random_state=random_state)
    # 预处理
    num_cols = X.columns
    num_transformer = Pipeline(steps=[('scaler', StandardScaler())])
    preprocessor = ColumnTransformer(transformers=[('num', num_transformer, num_cols),], remainder='passthrough')
    X_train = preprocessor.fit_transform(X_train)
    X_val = preprocessor.transform(X_val)
    X_test = preprocessor.transform(X_test)
    # 训练模型
    model = SVR(kernel="rbf", degree=3, gamma='scale', coef0=0, tol=1e-5, C=1, epsilon=1e-5, max_iter=1000)
    model.fit(X_train, y_train)
    # 推断
    y_pred_train = model.predict(X_train)
    mse_train = mean_squared_error(y_pred_train, y_train)
    y_pred_val = model.predict(X_val)
    mse_val = mean_squared_error(y_pred_val, y_val)
    # 记录
    mse_train_mice_pmm_list.append(mse_train)
    mse_val_mice_pmm_list.append(mse_val)
# 考虑插补不确定性的最终性能指标。
pooled_mse_train_mice_pmm = np.mean(mse_train_mice_pmm_list)
pooled_mse_val_mice_pmm = np.mean(mse_val_mice_pmm_list)
print(f'\n最终性能 - 训练 MSE: {pooled_mse_train_mice_pmm:.6f}, 验证 MSE: {pooled_mse_val_mice_pmm:.6f}')

结果

每种方法的训练和验证结果均使用均方误差（MSE）进行评估：

MICE with PMM：训练集：394.135692，验证集：368.203358
MICE with 正态线性回归：训练集：331.430123，验证集：308.422768
回归插补（基线）：训练集：412.053577，验证集：383.246492

两种 MICE 方法都取得了比单一回归插补基线更好的性能（更低的 MSE）。

MICE with 正态线性回归方法表现最佳，实现了最低的验证集 MSE（308.42）。

这种优越的性能可能归因于：

插补模型拟合度：MICE 使用的正态线性回归模型准确地捕捉了数据中潜在的关系。
预测一致性：PMM 方法使用随机抽样（随机性）来抽取值，这引入了固有的抽样噪声，并可能导致更高的 MSE。

总之，MICE 通过正确处理缺失数据的不确定性，成功地提高了模型性能，其中线性回归插补技术被证明对任务最有效。

结论

MICE 是一种有竞争力的插补方法，可用于从不完整数据中创建统计上有效的推断和稳健的预测模型。

在实验中，我们观察到 MICE 成功地提高了模型性能，优于基线线性回归插补。

展望未来，优化估计器、迭代次数或循环次数将进一步增强模型的能力。