1 单选题(每题 2 分,共 30 分)
第1题 运行下面程序后变量 a 的值是( )。
|-------------------------------------------------|
| 1│int a = 42; 2│int* p = &a; 3│*p = *p + 1; |
A. 42 B. 43 C. 编译错误 D. 不确定
解析:答案B。*p指向变量a,*p=*p+1即a=a+1,运行程序后变量a的值是43。故选B。
第2题 以下关于数组的描述中,( )是错误的。
A. 数组名是一个指针常量
B. 随机访问数组的元素方便快捷
C. 数组可以像指针一样进行自增操作
D. sizeof(arr)返回的是整个数组 arr 占用的字节数
解析:答案C。数组名表示首元素地址,类型为T* const(不可修改的指针),为指针常,A正确;通过下标(如arr[i])可O(1)时间复杂度访问任意元素,B正确;数组名虽然是首元素的地址(指针常量),但它不能直接进行自增操作(如arr++),C错误;sizeof作用于数组名时返回总大小(如int arr[5]返回5*sizeof(int)),D正确。故选C。
第3题 给定如下定义的数组arr,则 *(*(arr + 1) + 2) 的值是( )。
|-----------------------------------------------|
| 1│int arr[2][3] = {{1, 2, 3}, {4, 5, 6}}; |
A. 2 B. 5 C. 4 D. 6
解析:答案D。二维数组名退化为指针,指向数组的行,*(arr + 1)指向第2行第1个元素,再+2,指向第3个元素,*解引用获取指针指向元素的值,相当于arr[1][2],等于6。故选D。
第4题 下面这段代码会输出( )。
|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int add(int a, int b = 1); // 函数声明 2│ 3│int main() { 4│ cout << add(2) << " " << add(2, 3); 5│ return 0; 6│} 7│ 8│int add(int a, int b) { // 函数定义 9│ return a + b; 10│} |
A. 3 5 B. 编译失败:定义处少了默认参数
C. 运行错误 D. 链接失败:未定义引用
解析:答案A。add(2),a=2,b=1(默认),返回a+b=2+1=3;add(2, 3),a=2,b=3,返回a+b=2+3=5。选A。
第5题 下面这段代码会输出( )。
|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int x = 5; 2│ 3│void foo() { 4│ int x = 10; 5│ cout << x << " "; 6│} 7│ 8│void bar() { 9│ cout << x << " "; 10│} 11│ 12│int main() { 13│ foo(); 14│ bar(); 15│} |
A. 5 5 B. 10 10 C. 5 10 D. 10 5
解析:答案D。在所有函数外定义的int x=5是全局变量,在foo()函数中又定义了一个同名局部变量int x=10,所以第5行输出的x是局部变量x,输出10,如要输出 全局变量x,则需用::x表示;在bar()中没有定义同名局部变量x,所以第9行输出的x是全局变量x,输出5;总体输出10 5,故选D。
第6题 下面程序运行的结果是( )。
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│void increaseA(int x) { 2│ x++; 3│} 4│void increaseB(int* p) { 5│ (*p)++; 6│} 7│int main() { 8│ int a = 5; 9│ increaseA(a); 10│ cout << a << " "; 11│ increaseB(&a); 12│ cout << a; 13│} |
A. 6 7 B. 6 6 C. 5 6 D. 5 5
解析:答案C。increaseA()函数是值传递,第9行调用时将a的值 5传递给形参x,对x的修改不影响传递变量a,所以第10行输出的a的值 为5;increaseB()是指针传递,第11行调用时将a的地址传递给形参p,对*p就是对a的修改,(*p)++是指针指向类型变量自增,等价a++,所以第12行输出的a的值为6;总体输出5 6,故选C。
第7题 关于结构体初始化,以下四个选项中正确的是( )。
|----------------------------|
| 1│struct Point {int x,y;}; |
A. Point p = (1,2); B. Point p = {1,2}; C. Point p = new {1,2}; D. Point p = <1,2>;
解析:答案B。结构体初始化用{},排除A、D;B是列表初始化 ,x 和 y 分别被赋值为 1 和 2,B正确;new 返回的是指针 ,不能直接赋值给非指针变量,正确写法:
Point* p = new Point(1, 2);
D错误。故选B。
第8题 运行如下代码会输出( )。
|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│struct Cat { 2│ string name; 3│ int age; 4│}; 5│ 6│void birthday(Cat& c) { 7│ c.age++; 8│} 9│ 10│int main() { 11│ Cat kitty{"Mimi", 2}; 12│ birthday(kitty); 13│ cout << kitty.name << " " << kitty.age; 14│} |
A. Mimi 2 B. Mimi 3 C. kitty 3 D. kitty 2
解析:答案B。第11行定义了结构体结构体kitty,并初始化用name为"Mimi"、age为2,第12行用kitty对象(结构体)调用,第6行&引用接收,c相当于kitty的别名,对c的修改就是对kitty的修改,第7行对c的age自增,即由原来和2增为3,所以第13行输出为Mimi 3。故选B。
第9题 关于排序算法的稳定性,以下说法错误的是( )。
A. 稳定的排序算法不改变相等元素的相对位置
B. 冒泡排序是稳定的排序算法
C. 选择排序是稳定的排序算法
D. 插入排序是稳定的排序算法
解析:答案C。排序算法的稳定性定义即保证相等元素的原始相对顺序不变,所以A正确;冒泡排序仅交换相邻元素,若相等则不交换,因此是稳定的,所以B正确;选择排序在交换过程中可能破坏相等元素的相对顺序。例如,序列 [5, 8, 5, 2] 中,第一个 5 可能与 2 交换,导致两个 5 的相对位置改变,因此选择排序是不稳定的,所以C错误;插入排序(包括直接插入和折半插入)在插入相等元素时不会改变其相对位置,故稳定,所以D正确。故选C。
第10题 下面代码试图实现选择排序,使其能对数组 nums 排序为升序,则横线上应分别填写( )。
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│void selectionSort(vector& nums) { 2│ int n = nums.size(); 3│ for (int i = 0; i < n - 1; ++i) { 4│ int minIndex = i; 5│ for (int j = i + 1; j < n; ++j) { 6│ if ( __________ ) { // 在此处填入代码 7│ minIndex = j; 8│ } 9│ } 10│ ____________________; // 在此处填入代码 11│ } 12│} |
|----|----------------------------------------------------------------------|----|---------------------------------------------------------------------|
| A. | 1│nums[j] < nums[minIndex] 2│swap(nums[i], nums[minIndex]) | B. | 1│nums[j] > nums[minIndex] 2│swap(nums[i], nums[minIndex]) |
| C. | 1│nums[j] <= nums[minIndex] 2│swap(nums[j], nums[minIndex]) | D. | 1│nums[j] <= nums[minIndex] 2│swap(nums[i], nums[j]) |
解析:答案A。升序排序:小的元素排到前面,大的元素排到后面,即从小到大排。这是选择排序,需在未排序部分找到最小值 ,因此应使用 nums[j] < nums[minIndex]; 比较,排除C、D;找到最小值后,需将其与当前未排序部分的第一个元素(nums[i])交换,即 swap(nums[i], nums[minIndex])。B的比较条件错误(找最大值),A正确。故选A。
第11题 下面程序实现插入排序(升序排序),则横线上应分别填写( )。
|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│void insertionSort(int arr[], int n) { 2│ for (int i = 1; i < n; i++) { 3│ int key = arr[i]; 4│ int j = i - 1; 5│ while ( j >= 0 && ____________________ ) { // 在此处填入代码 6│ arr[j + 1] = arr[j]; 7│ j--; 8│ } 9│ ____________________; // 在此处填入代码 10│ } 11│} |
|----|----------------------------------------|----|----------------------------------------|
| A. | 1│arr[j] > key 2│arr[j + 1] = key | B. | 1│arr[j] < key 2│arr[j + 1] = key |
| C. | 1│arr[j] > key 2│arr[j] = key | D. | 1│arr[j] < key 2│arr[j] = key |
解析:答案A。插入排序需将 key(当前元素)插入到已排序部分的正确位置(arr[j]≤key)。当 arr[j] > key 时,需将 arr[j] 后移,为 key 腾出位置,所以排除B、D;找到 key 的正确位置后,需将 key 赋给 arr[j + 1](即 key 应插入的位置(找到的位置之后)),所以C、D错误。故选A。
第12题 关于插入排序的时间复杂度,下列说法正确的是( )。
A. 最好情况和最坏情况的时间复杂度都是𝑂(𝑛²)
B. 最好情况是𝑂(𝑛),最坏情况是𝑂(𝑛²)
C. 最好情况是𝑂(𝑛),最坏情况是𝑂(2ⁿ)
D. 最好情况是𝑂(𝑛²),最坏情况是𝑂(2ⁿ)
解析:答案B。关于插入排序的时间复杂度,最好情况(数组已有序):每次插入仅需比较一次且无需移动元素,时间复杂度为𝑂(𝑛);最坏情况(数组完全逆序):每次插入需比较并移动所有已排序元素,总时间复杂度为𝑂(𝑛²)。所以插入排序的时间复杂度,最好情况是𝑂(𝑛),最坏情况是 𝑂(𝑛²),B正确。故选B。
第13题 小杨正在爬楼梯,需要𝑛阶才能到达楼顶,每次可以爬1阶或2阶,求小杨有多少种不同的方法可以爬到楼顶,横线上应填写( )。
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int climbStairs(int n) { 2│ if (n <= 2) return n; 3│ int prev2 = 1; 4│ int prev1 = 2; 5│ int current = 0; 6│ for (int i = 3; i <= n; ++i) { 7│ ________________ // 在此处填入代码 8│ 9│ } 10│ return current; 11│} |
|----|----------------------------------------------------------------|----|----------------------------------------------------------------|
| A. | 1│prev2 = prev1; 2│prev1 = current; 3│current = prev1 + prev2; | B. | 1│current = prev1 + prev2; 2│prev2 = prev1; 3│prev1 = current; |
| C. | 1│current = prev1 + prev2; 2│prev1 = current; 3│prev2 = prev1; | D. | 1│prev1 = current; 2│prev2 = prev1; 3│current = prev1 + prev2; |
解析:答案B。推导:要上n阶台阶,可从n-2阶跨2阶到达,也可从n-1阶跨1阶到达,总方法数是到n-2阶的方法+到n-1阶的方法,设f(n)是到达n阶的方法,则f(n)=f(n-1)+f(n-2)。第1阶台阶只能跨1阶,1种方法,f(1)=1;第2阶台阶可跨1阶到1阶、再跨1阶到2阶,也可跨2阶到2阶,共2种方法,f(2)=2。所以根据题目提供的程序应填写
current = prev1 + prev2;
prev2 = prev1;
prev1 = current;
逻辑顺序 :首先计算当前值:current = prev1 + prev2(因为当前方法数是前两种方法数之和)
然后更新变量:prev2 取旧值 prev1,prev1 取新值 current。
先赋值再计算,会导致 current 初始值错误,A错误;C更新顺序错误,prev2 会丢失旧值,错误;D完全颠倒了计算和赋值的顺序,错误。故选B。
第14题 假设有一个班级的成绩单,存储在一个长度为 n 的数组 scores 中,每个元素是一个学生的分数。老师 想要找出 所有满足 scores[i] + scores[j] + scores[k] == 300 的三元组,其中 i < j < k。下面代码实现该功 能,请问其时间复杂度是( )。
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1│int cnt = 0; 2│for (int i = 0; i < n; i++) { 3│ for (int j = i + 1; j < n; j++) { 4│ for (int k = j + 1; k < n; k++) { 5│ if (scores[i] + scores[j] + scores[k] == 300) { 6│ cnt++; 7│ } 8│ } 9│ } 10│} |
A. 𝑂(𝑛) B. 𝑂(𝑛²) C. 𝑂(𝑛³) D. 𝑂(2ⁿ)
解析:答案C。外层循环:i从0到n-1,执行n次,中层循环:j从i+1到n-1,最坏情况下约执行n/2次;内层循环:k从j+1到n-1,最坏情况下约执行n/3次;最内层操作:条件判断是𝑂(1)的常数时间操作。总时间复杂度为三重循环的乘积:𝑂(𝑛) ×𝑂(𝑛) ×𝑂(𝑛) = 𝑂(𝑛³)
具体来说:当𝑛很大时,循环次数约为𝑛(𝑛-1)(𝑛-2)/6,最高次为𝑛³,所以时间复杂度为𝑂(𝑛³)。故选C。
第15题 关于异常处理,以下说法错误的是( )。
A. try 块中的代码可能会抛出异常
B. catch 块可以有多个,处理不同类型的异常
C. throw 语句用于抛出异常
D. 所有异常都必须被捕获,否则程序会崩溃
解析:答案D。try 块中的代码可能会抛出异常,这是 try-catch 机制的基本用途,A正确; catch 块可以有多个,分别处理不同类型的异常(如 catch (IOException e) 和 catch (SQLException e)),B正确;throw 语句用于手动抛出异常(如 throw new IllegalArgumentException("Invalid input");),C正确;并非所有异常都必须被捕获。未被捕获的异常会向上层调用栈传播,如果最终未被处理,程序会终止并打印错误信息,但并非所有情况都会导致程序崩溃(例如某些异常可以被 finally 块或全局异常处理器处理),D错误。故选D。
2 判断题(每题 2 分,共 20 分)
第1题 以下代码能正确初始化指针。
|-----------------------------|
| 1│int a = 5; 2│int *p = a; |
解析:答案╳。这段代码试图将一个整型变量 a 直接赋值给一个整型指针 p,这是不正确的,问题是类型不匹配 :a 是 int 类型,而 p 是 int* 类型(指针)。不能直接将一个普通变量赋值给指针,指针应该存储变量的地址 ,而不是变量的值。正确的初始化方式 :如果要让 p 指向 a,应该使用取地址运算符 &:int *p = &a;。故错误。
第2题 执行下面C++代码将输出 11 。
|-------------------------------------------------------------------------------------------------------|
| 1│int x = 10; 2│void f() { 3│ int x = x + 1; 4│ cout << x << endl; 5│} 6│int main() { 7│ f(); 8│} |
解析:答案╳。这段代码的输出结果不是 11 ,而是未定义行为 (Undefined Behavior, UB) ,可能输出一个随机值或导致程序崩溃。问题原因:变量作用域冲突 :在函数 f() 中,int x = x + 1; 声明了一个新的局部变量 x,但它的初始化表达式 x + 1 中的 x 是未初始化的局部变量 (不是全局变量 x = 10)。C++ 的变量作用域规则规定:局部变量 x 在声明完成后才可见,因此在初始化时使用的是自身的未定义值 ,而不是全局变量 x。未定义行为 :使用未初始化的局部变量 x 的值(x + 1)是未定义行为,可能导致程序输出任意值或崩溃。故错误。
第3题 以下C++代码合法。
|---------------------------------------------------------------------------------------------------------------|
| 1│struct Student { 2│ string name; 3│ int age; 4│ float score; 5│}; 6│Student* students = new Student[20]; |
解析:答案√。这段 C++ 代码定义结构体 Student:包含三个成员变量:name(string 类型)、age(int 类型)、score(float 类型)。动态分配数组 :Student* students = new Student[20]; 在堆内存中分配了20 个 Student结构体的连续空间 ,并返回首地址给指针 students。代码语法正确,符合 C++ 规范,是合法的。 故正确。
第4题 执行下面C++代码将输出 10 。
|-----------------------------------------------------------------------------------------------------------------------------------|
| 1│void func(int* p) { 2│ *p = 10; 3│} 4│ 5│int main() { 6│ int a = 5; 7│ func(&a); 8│ cout << a << endl; 9│ return 0; 10│} |
解析:答案√。这段代码 指针传递 : func(&a) 将变量 a 的地址传给函数 func ,函数内部通过 *p = 10 修改了 a 的值 (p 指向 a) 。 修改后,a 的值变为 10,因此 cout << a 输出 10。故正确。
第5题 下面代码将二维数组 arr 传递给函数 f ,函数内部用 arr[i][j] 访问元素,函数参数声明为 int arr[] [4] 是错误的。
|-----------------------------------------------------------------------------------------------------------------------------------------------|
| 1│void f(int arr[][4], int rows) { 2│ // 访问 arr[i][j] 3│} 4│ 5│int main() { 6│ int arr[3][4] = { /* 初始化 */ }; 7│ f(arr, 3); 8│} |
解析:答案╳。C/C++**数组参数规则 :当传递二维数组给函数时,第一维的大小可以省略** (因为编译器可以通过指针运算推导),但第二维必须明确指定 (否则无法计算元素偏移)。所以题目中的函数参数声明 int arr[][4] 是正确的,函数内部可以通过 arr[i][j] 访问元素,只要0 < i < rows 且0 < j < 4。故错误。
第6题 递推是在给定初始条件下,已知前一项(或前几项)求后一项的过程。
解析:答案√。递推的核心是通过已知的初始条件和递推关系逐步推导后续项。具体要点为:初始条件:必须明确数列的前几项(如第1项或前几项)作为计算基础。递推关系:需定义当前项与前一项(或前几项)的数学关系(如斐波那契数列的𝑓(𝑛) = 𝑓(𝑛−1) + 𝑓(𝑛−2))。逐步推导:通过初始条件和递推公式,可逐项计算出后续值。故正确。
第7题 虽然插入排序的时间复杂度为 ,但由于单元操作相对较少,因此在小数据量的排序任务中非常受欢迎。
解析:答案√。插入排序的时间复杂度为𝑂(𝑛²),但在小规模或近乎有序的数据中表现优异,原因如下:单元操作较少(插入排序的核心操作是"比较"和"移动",其内层循环的移动次数通常较少(尤其在数据部分有序时)。例如,若数据已基本有序,每次插入仅需少量比较和移动,实际效率接近𝑂(𝑛))。小数据量优势(当数据规模较小时,𝑂(𝑛²)的常数因子(如比较和移动的固定开销)可能优于更复杂算法(如快速排序)的递归开销。稳定性与原地性(插入排序是稳定排序(相等元素顺序不变)且空间复杂度为𝑂(1),适合对内存敏感或需保持数据顺序的场景。故正确。
第8题 对整数数组 {4, 1, 3, 1, 5, 2} 进行冒泡排序(将最大元素放到最后),执行一轮之后是 {4, 1, 3, 1, 2, 5} 。
解析:答案╳。冒泡排序第一轮:{4, 1, 3, 1, 5, 2}→{1, 4, 3, 1, 5, 2}→{1, 3, 4, 1, 5, 2}→{1, 3, 1, 4, 5, 2}→{1, 3, 1, 4, 5, 2}→{1, 3, 1, 4, 2, 5},执行一轮之后是{1, 3, 1, 4, 2, 5}不是{4, 1, 3, 1, 2, 5}。故错误。
第9题 以下代码只能捕获 int 类型异常。
|----------------------------------------------------------------------------------------------------------------|
| 1│int main() { 2│ try { 3│ throw 42; 4│ } catch (...) { 5│ cout << "Caught" << endl; 6│ } 7│ return 0; 8│} |
解析:答案╳。题目提供的代码使用了 catch (...),这是C++中的通用异常捕获 语法,可以捕获任意类型 的异常(包括 int、自定义类、标准异常等),而不仅限于 int 类型。题目描述"只能捕获 int 类型异常"是不正确的。故错误。
第10题 以下代码将 Hello 写入文件 data.txt 。
|--------------------------------------------------------------------------|
| 1│ofstream file("data.txt"); 2│cout<<"Hello"<< endl; 3│file.close(); |
解析:答案╳。题目提供的代码存在逻辑错误:题目给的第1行是以读文件方式文件对象file,打开"data.txt",非重定向,所以cout 会将 "Hello" 输出到控制台(屏幕),而非写入文件。故错误。
3 编程题(每题 25 分,共 50 分)
3.1 编程题 1
- 试题名称:排兵布阵
- 时间限制:1.0 s
- 内存限制:512.0 MB
3.1.1题目描述
作为将军,你自然需要合理地排兵布阵。地图可以视为𝑛行𝑚列的网格,适合排兵的网格以1标注,不适合排兵的网格以0标注。现在你需要在地图上选择一个矩形区域排兵,这个矩形区域内不能包含不适合排兵的网格。请问可选择的矩形区域最多能包含多少网格?
3.1.2 输入格式
第一行,两个正整数𝑚, 𝑛,分别表示地图网格的行数与列数。
接下来𝑛行,每行𝑚个整数𝑎ᵢ, ₁,𝑎ᵢ, ₂,...,𝑎ᵢ, ₘ,表示各行中的网格是否适合排兵。
3.1.3 输出格式
一行,一个整数,表示适合排兵的矩形区域包含的最大网格数。
3.1.4 样例
3.1.4.1 输入样例1
|---------------------------------------|
| 1│4 3 2│0 1 1 3│1 0 1 4│0 1 1 5│1 1 1 |
3.1.4.2 输出样例1
|-----|
| 1│4 |
3.1.4.3 输入样例2
|-------------------------------------------|
| 1│3 5 2│1 0 1 0 1 3│0 1 0 1 0 4│0 1 1 1 0 |
3.1.4.4 输出样例2
|-----|
| 1│3 |
3.1.5 数据范围
对于所有测试点,保证1≤𝑛,𝑚≤12,0≤𝑎ᵢ,ⱼ≤1。
3.1.6 编写程序
方法一:
题目要求在地图网格(0/1矩阵)中找出最大的全1矩形区域,因为𝑛,𝑚都不大,其核心算法可通过枚举所有可能的子矩阵并验证其有效性。算法步骤:
1.输入处理:读取n行m列的矩阵数据,0表示不可排兵,1表示可排兵。
2.预处理:计算二维前缀和saᵢⱼ,saᵢⱼ=从(1,1)到(i,j)的子矩阵和(全部0、1和)。
3.枚举策略:通过左上角坐标(x1,y1)到右下角坐标(x2,y2)四重循环遍历所有可能的子矩阵边界,求(x1,y1)到(x2,y2)区域内的和(1的个数)。
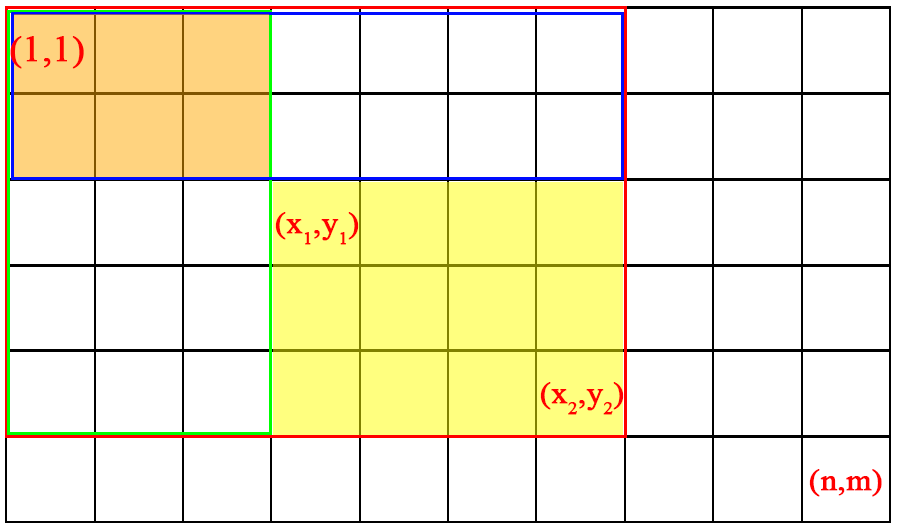
图1 区域内1的个数计算用图
如图1所示,(x1,y1)到(x2,y2)区域内1的和sum(黄色区)等于红框区域内1的和sa[x2][y2] ,减去蓝色框区域内1的和sa[x2][y1-1],减去绿框区域内1的和sa[x1-1][y2],其中橙色区减了2次,需加橙色区的和sa[x1-1][y1-1],合计:
sum=sa[x2][y2] - sa[x2][y1 - 1] - sa[x1 - 1][y2] + sa[x1 - 1][y1 - 1];区域大小为(x2 - x1 + 1) * (y2 - y1 + 1)
4.有效性验证:检查子矩阵内所有元素是否为1,如sun=(x2 - x1 + 1) * (y2 - y1 + 1),则为全1。
5.时间复杂度:𝑂(𝑛²𝑚²)=𝑂(12²×12²)=20736<10⁵,不会超时。
完整参考程序如下:
cpp
#include <iostream>
using namespace std;
const int N = 15; // 1≤n, m≤12
int n, m, a[N][N], sa[N][N], maxn = 0; // maxn为最大网格数
int main() {
cin >> n >> m; // 输入n, m
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) cin >> a[i][j]; // 输入aᵢⱼ
for (int i = 1; i <= n; i++) // 计算二维前缀和saᵢⱼ
for (int j = 1; j <= m; j++)
sa[i][j] = sa[i - 1][j] + sa[i][j - 1] - sa[i - 1][j - 1] + a[i][j];
for (int x1 = 1; x1 <= n; x1++) // 枚举所有子矩阵。x1,y1左上角坐标
for (int y1 = 1; y1 <= m; y1++) // x2,y2右下角坐标
for (int x2 = x1; x2 <= n; x2++)
for (int y2 = y1; y2 <= m; y2++) { // saᵢⱼ存储从(1,1)到(i,j)的子矩阵和(全部0、1和)
int sum = sa[x2][y2] - sa[x2][y1 - 1] - sa[x1 - 1][y2] + sa[x1 - 1][y1 - 1];
if (sum == (x2 - x1 + 1) * (y2 - y1 + 1)) // 如(x1,y1)到(x2,y2)的子矩阵和=区域大小(全1)
maxn = sum > maxn? sum: maxn; // 与原最大值比较取大者
}
cout << maxn << endl;
return 0;
}方法二:
题目要求在地图网格(0/1矩阵)中找出最大的全1矩形区域,因为𝑛,𝑚都不大,其核心算法可通过枚举所有可能的子矩阵并验证其有效性。算法步骤:
1.输入处理:读取n行m列的矩阵数据,0表示不可排兵,1表示可排兵。
2.枚举策略:通过左上角坐标(x1,y1)到右下角坐标(x2,y2)四重循环遍历所有可能的子矩阵边界,用一个循环判断(x1,y1)到(x2,y2)区域内是否全1。判断方法:设flg=1,然后用flg按位与区域内各元素,如遇0,则flg &= a[x][y2]后,flg=0,不计数。如flg=1,计算区域大小并与最大值maxn比较。
3.时间复杂度:𝑂(𝑛³𝑚²)=𝑂(12³×12²)=248832<10⁶,不会超时。
完整参考程序如下:
cpp
#include <iostream>
using namespace std;
const int N = 15; // 1≤n, m≤12
int n, m;
int a[N][N];
int maxn;
int main() {
cin >> n >> m; // 输入n, m
cout << n << "," << m << endl;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) cin >> a[i][j]; // 输入aᵢⱼ
for (int x1 = 1; x1 <= n; x1++) // 左上角坐标x1
for (int y1 = 1; y1 <= m; y1++) // 左上角坐标y1
for (int x2 = x1; x2 <= n; x2++) { // 右下角坐标x2
int flg = 1; // 设标志为1
for (int y2 = y1; y2 <= m; y2++) { // 右下角坐标y2
for (int x = x1; x <= x2; x++) flg &= a[x][y2]; // 循环计算flg & aᵢⱼ
if (!flg) break; // aᵢⱼ有0则flg为0,1 & 0 = 0,不计数
maxn = (y2-y1+1)*(x2-x1+1)>maxn? (y2-y1+1)*(x2-x1+1): maxn; // 两者取大者
}
}
cout << maxn << endl;
return 0;
}3.2 编程题 2
- 试题名称:最长连续段
- 时间限制:1.0 s
- 内存限制:512.0 MB
3.2.1题目描述
对于𝑘个整数构成的数组[𝑏₁,𝑏₂,...,𝑏ₖ],如果对1≤𝑖<𝑘都有𝑏ᵢ₊₁=𝑏ᵢ+1,那么称数组𝑏是一个连续段。
给定由𝑛个整数构成的数组[𝑎₁,𝑎₂,...,𝑎ₙ],你可以任意重排数组𝑎中元素顺序。请问在重排顺序之后,𝑎所有是连续段的子数组中,最长的子数组长度是多少?
例如,对于数组[1,0,2,4],可以将其重排为[4,0,1,2],有以下10个子数组:
4\],\[0\],\[1\],\[2\],\[4,0\],\[0,1\],\[1,2\],\[4,0,1\],\[0,1,2\],\[4,0,1,2
其中除[4,0], [4,0,1], [4,0,1,2]以外的子数组均是连续段,因此是连续段的子数组中,最长子数组长度为3。
3.2.2 输入格式
第一行,一个正整数𝑛,表示数组长度。
第二行,𝑛个整数𝑎₁,𝑎₂,...,𝑎ₙ,表示数组中的整数。
3.2.3 输出格式
一行,一个整数,表示数组𝑎重排顺序后,所有是连续段的子数组的最长长度。
3.2.4 样例
3.2.4.1 输入样例1
|---------------|
| 1│4 2│1 0 2 4 |
3.2.4.2 输出样例1
|-----|
| 1│3 |
3.2.4.3 输入样例2
|-------------------------|
| 1│9 2│9 9 8 2 4 4 3 5 3 |
3.2.4.4 输出样例2
|-----|
| 1│4 |
3.2.5 数据范围
对于40%的测试点,保证1≤𝑛≤8。
对于所有测试点,保证1≤𝑛≤10⁵,-10⁹≤𝑎ᵢ≤10⁹。
3.2.6 编写程序
方法一:
题目要求计算连续段的子数组中最长子数组长度。思路:根据连续段的定义,升序排序后连续段会排序在一个连续段内,但可能有重复数据,重复数据会连在一起,可考虑去重,然后计算连续段的子数组中最长子数组长度。
排序用C++的sort()可实现升序排序,时间复杂度为𝑂(𝑛log𝑛)。
去重用C++的unique()可排序后数组实现去重,时间复杂度为𝑂(𝑛)。
计算连续段的子数组中最长子数组长度采用循环计算,时间复杂度为𝑂(𝑛)。
总体时间复杂度为𝑂(𝑛log𝑛)
最大n=10⁵,时间复杂度为𝑂(𝑛log𝑛)= 时间复杂度为𝑂(10⁵log10⁵)≈1151292.5465<10⁷,不会超时。
算法步骤:
1.输入处理:读取n个数据组元素。
2.排序、去重。
- 计算连续段的子数组中最长子数组长度。
完整参考程序如下:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5; // n≤10⁵
int n, a[N], last, maxn, mx;
int main() {
cin >> n; // 输入元素个数
for (int i = 1; i <= n; i++) cin >> a[i]; // 输入n个数组元素
sort(a + 1, a + n + 1); // 升序排序
int n1 = unique(a+1, a + n + 1) - (a+1); // 去重,n1为不重复无数个数
last = a[1];
maxn = mx = 1;
for (int i = 1; i <= n1; i++) {
if (a[i] == last + 1) maxn++; // 连续数maxn计数
else maxn = 1; // 非连续数maxn初始化为1
last = a[i]; // 调整last为刚处理的元素
mx = max(maxn, mx); // 求最大maxn
}
cout << mx;
return 0;
}方法二:
题目要求计算连续段的子数组中最长子数组长度。思路:根据连续段的定义,升序排序后连续段会排序在一个连续段内,重复数据会连在一起,在计算连续段的子数组中子数组长度时,如遇前后数据相同就跳过不处理,前后差1计数,其他计数置1。
排序用C++的sort()可实现升序排序,时间复杂度为𝑂(𝑛log𝑛)。
计算连续段的子数组中最长子数组长度采用循环计算,时间复杂度为𝑂(𝑛)。
总体时间复杂度为𝑂(𝑛log𝑛)
最大n=10⁵,时间复杂度为𝑂(𝑛log𝑛)= 时间复杂度为𝑂(10⁵log10⁵)≈1151292.5465<10⁷,不会超时。
算法步骤:
1.输入处理:读取n个数据组元素。
2.排序。
- 计算连续段的子数组中最长子数组长度(剔除重复数据)。
完整参考程序如下:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5; // n≤10⁵
int n, a[N], last, maxn, mx;
int main() {
cin >> n; // 输入元素个数
for (int i = 1; i <= n; i++) cin >> a[i]; // 输入n个数组元素
sort(a + 1, a + n + 1); // 升序排序
last = a[1];
maxn = mx = 1;
for (int i = 1; i <= n; i++) {
if (a[i] == last) continue; // 重复数跳过不处理
if (a[i] == last + 1) maxn++; // 连续数计数
else maxn = 1; // 非连续数maxn初始化为1
last = a[i]; // 调整last为刚处理的元素
mx = max(maxn, mx); // 求最大maxn
}
cout << mx << endl;
return 0;
}