文章目录
快乐数
一.题目描述

快乐数 => 这个数字的每一位数字的平方和最终为1就是快乐数,否则不是
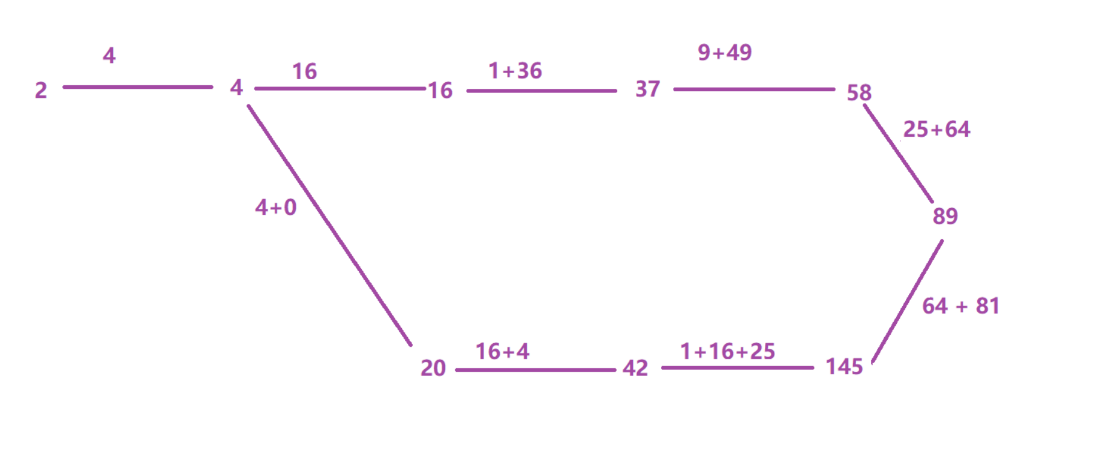
return true
以上这种情况就是快乐数
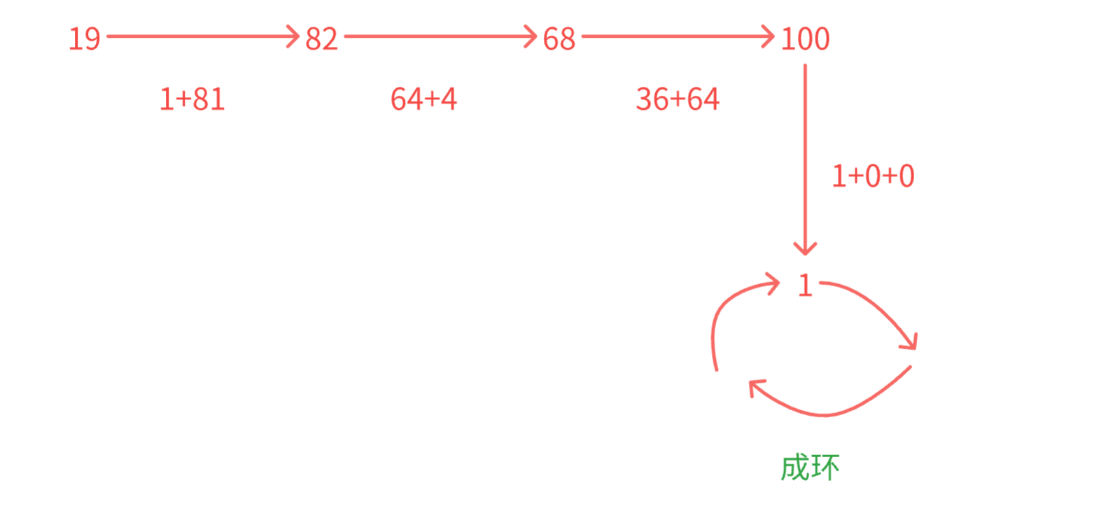
还有一种情况也会成环但是环内的值并不是1 =>不是快乐数
return false
二.题目解析
回想一下我们在刷题专栏中的链表篇接触过一道题,判断链表是否有环
对于一个数,经过快乐数的定义变换后,是一定会成环的(这个可以用鸽巢定理证明感兴趣的同学可以搜搜看),并且题目中也给了提示,若没有提示,我们也可以自己证明
证明快乐数 一定成环
鸽巢原理:n个巢,n+1只鸽子,至少有一个巢,里面的鸽子数大于1
int 最大值 2^23-1 是一个10位整数
闹我们使用9999999999(10个9)来转换
就是81*10=810
所以快乐数的值的区间一定是[0,810],我们巢穴出来了,随便找一个数,让他经理快乐数的811次转换,转换得数一定在[0,810]区间内,在转换811次之内,一定会出现重复的数,也就一定会成环
三.解题方法 --快慢双指针
在这道题里,我们可以把变换过程中的数,抽象成指针,相当于经历一次变换就是指针执行一次
1.定义双指针
2.慢指针每次向后移动一步,快指针每次向后移动两步
3.一定有环,两个指针相遇时的值判断是否为1即可
四.编写代码
因为每一次快乐数转换都要求这个数的每一位的平方,干脆把这个过程封装成一个方法bitSum(),直接返回平方和
java
class Solution {
public int bitSum(int n){
//返回 n 这个数的每一位上的平方和
int sum=0;
while(n!=0){
int t= n%10;//找到最后一位
sum+=t*t;//拿到平方和
n/=10;//干掉最后一位
}
return sum;
}
public boolean isHappy(int n) {
//快乐数
/*
慢指针每次向后一步,快指针每次向后两步,一定会在环里相遇
判断相遇时的值即可
*/
int slow=n,fast=bitSum(n);
while(slow!=fast){
slow=bitSum(slow);
fast=bitSum(bitSum(fast));
}
return slow==1;
}
}盛水最多的容器
一.题目解析
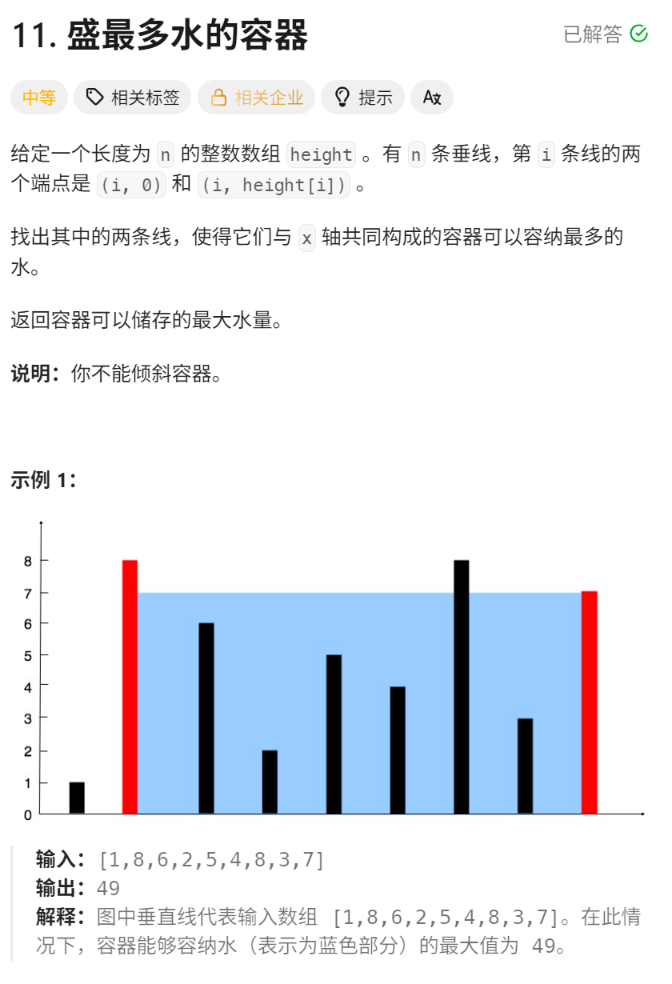
木桶效应: V=min(left,right) * (right-left)
二.解题方法
1.暴力枚举:两层for,left固定左边的柱子,right依次枚举右边的柱子;一轮结束后left固定第二根柱子,以此类推,算出所有的体积找最大值,但这样肯定会超时的 -- O(n^2)
2.利用单调性,使用双指针

right固定为4 left向内枚举,一共三种情况:
1.left所指高度 < 4 减小*减小 =>减小
2.left所指高度 = 4 不变
3.left所指高度 > 4 不变
无论是哪种情况,向内枚举的V一直都是减小的,我们要找最大的容器,那么我们就可以大胆舍弃当前双指针 中的较小的值,将较大的值固定,当然若两个值相等舍弃谁都行 --O(n)
总结:谁小移动谁
三.编写代码
java
class Solution {
//解法一:暴力枚举 所有情况都算出来 两层for循环 超时报错
//解法二:v=h*w
/*
利用单调性,使用双指针解决
*/
public int maxArea(int[] height) {
int left=0,right=height.length-1;
int ret=0;
while(left<right){
int v=Math.min(height[left],height[right])*(right-left);
//体积
ret=Math.max(ret,v);
if(height[left]<height[right]){
left++;
}else{
right--;
}
}
return ret;
}
}和为S的两个数
一.题目描述

二.解题方法
1.暴力枚举O(N^2):固定一个数,让这个数和另一个数匹配相加=target,则返回否则固定下一个数,两层for,时间复杂度太大了,题目给的是有序数组,利用单调性
2.利用单调性,使用双指针O(N)
两数之和sum与target大小关系无非三种情况:
1.sum<target
2.sum>target
3.sum=target
利用单调性
若sum<target =>left++
若sum>target =>right--
若sum=target =>return
三.编写代码
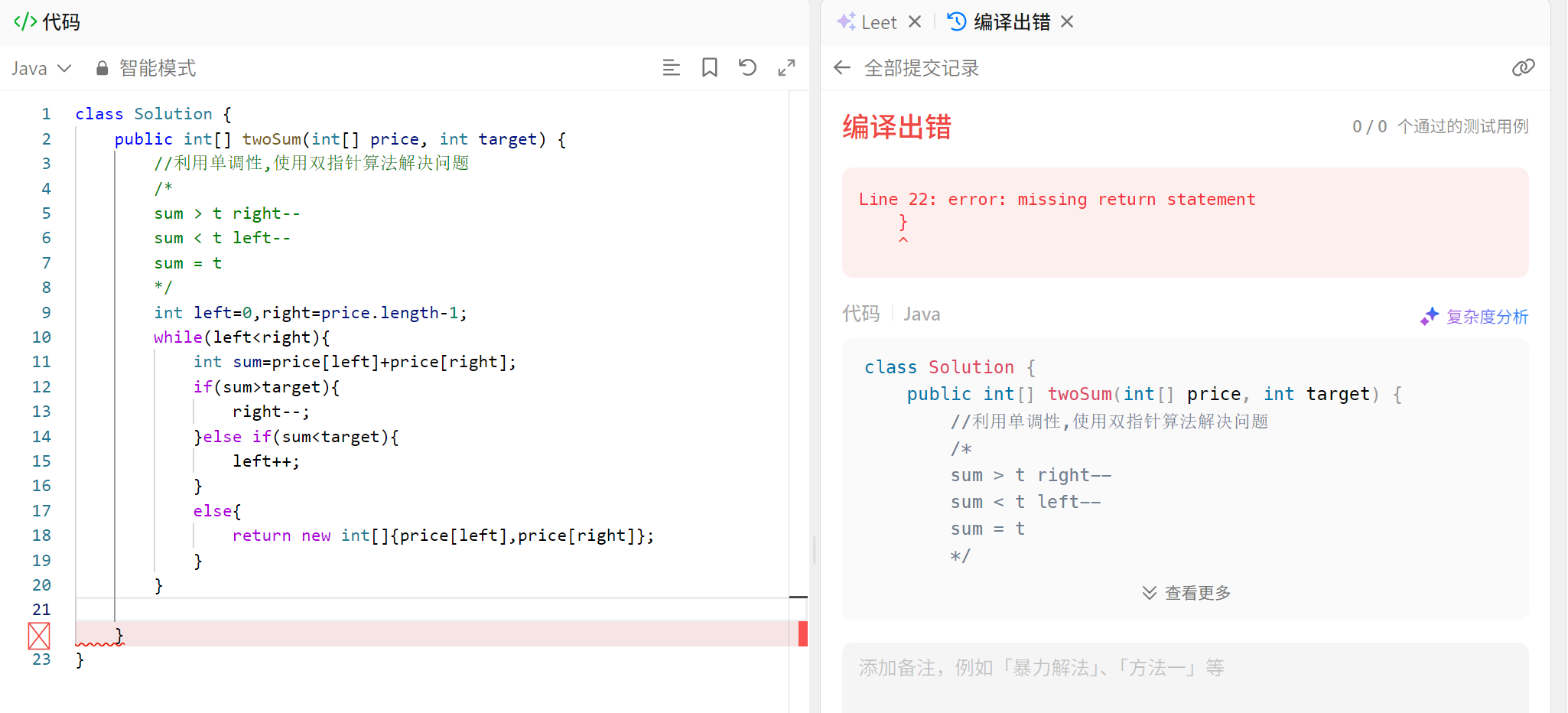
报错原因:编译器认为我们没有返回值,不对呀我们写了呀,为什么会判定没有返回值??
我们必须保证所有路径都有返回值,但我们的上述代码,如果没有两数之和为target,就不会有返回值
所以为了照顾编辑器,强行返回一个值,告诉编译器我们是有返回值的
java
class Solution {
public int[] twoSum(int[] price, int target) {
//利用单调性,使用双指针算法解决问题
/*
sum > t right--
sum < t left--
sum = t
*/
int left=0,right=price.length-1;
while(left<right){
int sum=price[left]+price[right];
if(sum>target){
right--;
}else if(sum<target){
left++;
}
else{
return new int[]{price[left],price[right]};
}
}
//照顾编译器一定要有返回值
return new int[]{0};//随便返回一个值
}
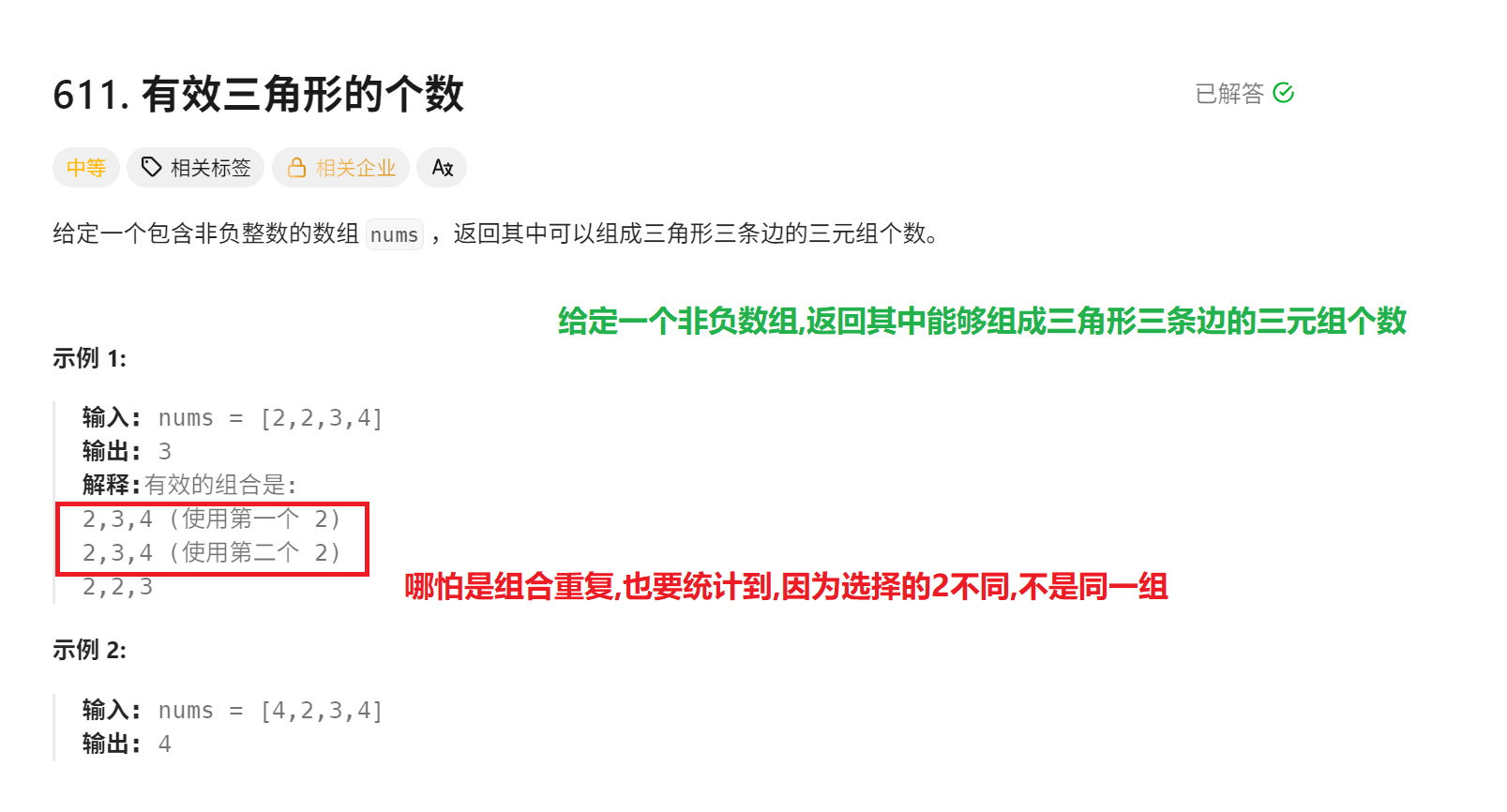
}有效三角形的个数
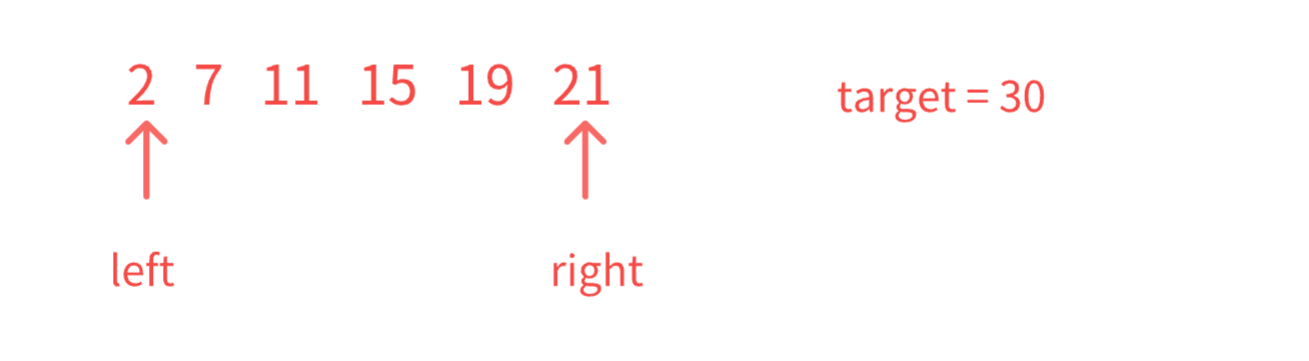
一.题目描述
二.题目解析
1.如何判断
利用任意两边之和大于第三边,就可以判断是否能组成三角形
(a+b>c)&&(a+c>b)&&(b+c>a),这种方法虽然简单,但是要判断三次
优化一下:将三个数排序,最小的两个数之和大于第三边,那么无论是两个小的数中的哪一个+大的数 都一定 > 另一个小数这样可以大大提升判断的效率
这里可能会有疑问,不是只优化了两次判断吗,时间复杂度感觉也没啥提升
如何提升了效率
提升点1 : 若使用暴力解法 => 三层for => O(N^3)最里面的循环中还要check一次是否有效 => 3*O(N^3)
若我们将数组排序后使用我们的优化方法 时间复杂度为 O(N^3+N*logN)
NlogN 可是比 2 N^3 效率高的多,除此之外
提升点2:排好序,可以利用单调性,使用双指针
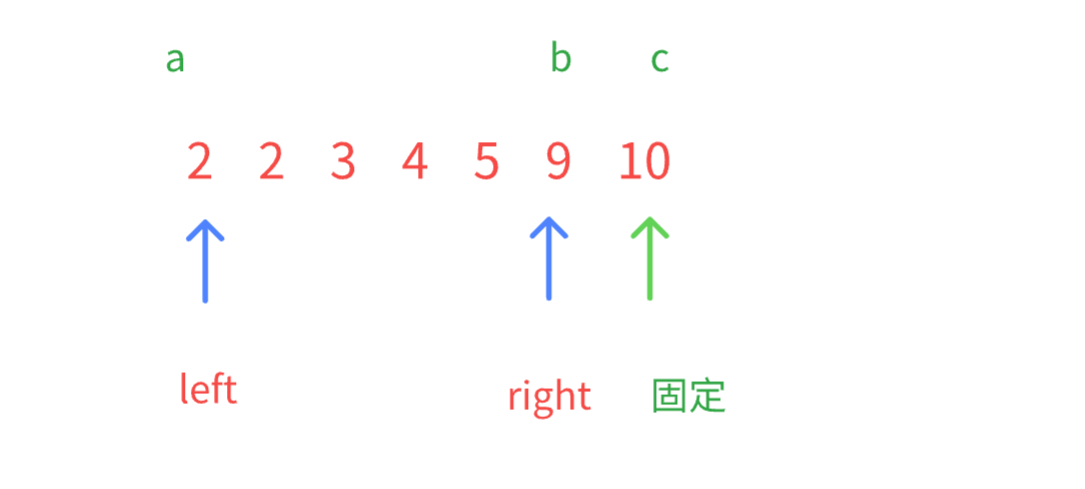
a+b 与 c 无非两种情况
1.a+b > c -->ok
2.a+b <= c 无法构成
情况一:中间的数据 都是 > a 所以不必枚举了,符合个数= right-left 然后right--情况二: 2+5 < 10 ,数据小了 => left++ 判断是否能构成了,不构成就重复上述操作
能构成就 right -- 不能构成就 left++
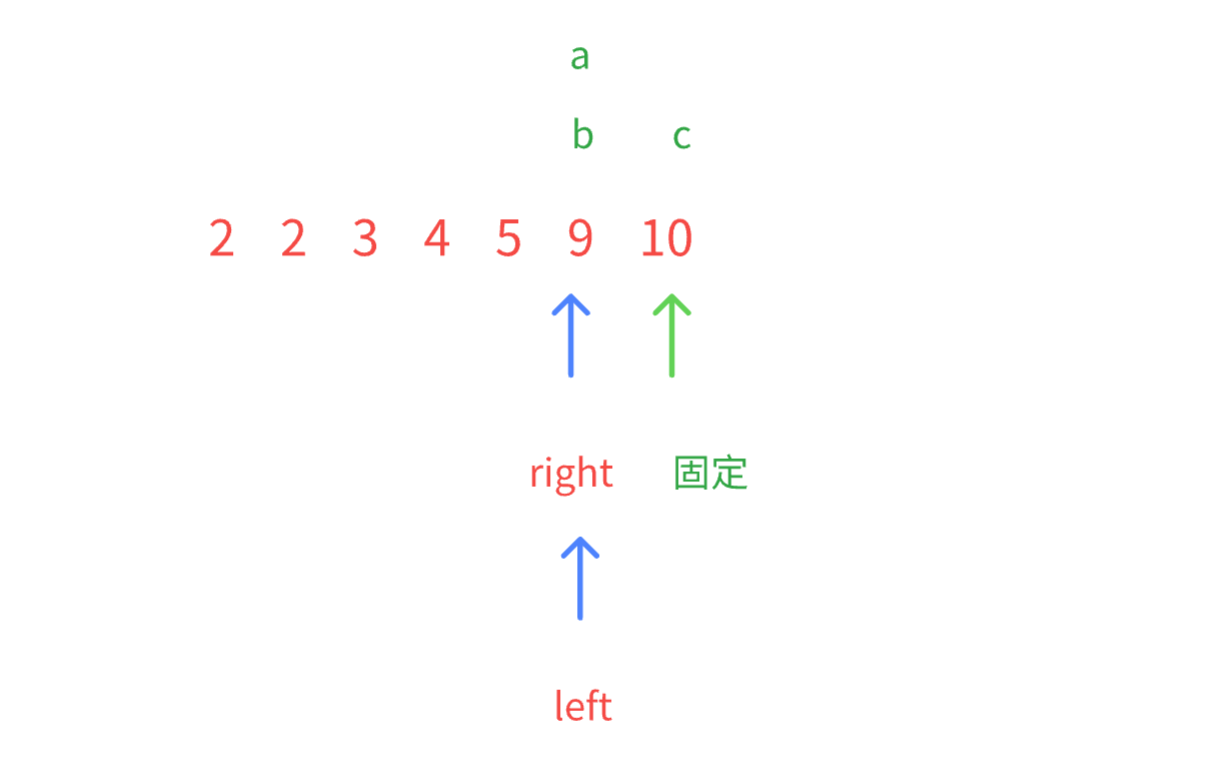
直到双指针相遇,说明当前固定C 的情况都已经找到了,这时我们就要移动固定为倒数第二大的数了
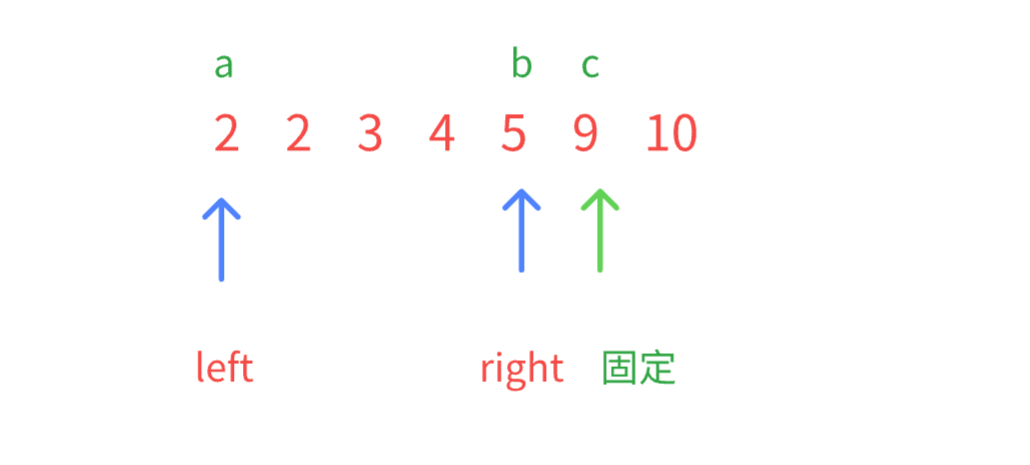
步骤总结:
1.先排序,方便判断
2.记录能够构成三角形的个数
3.先固定最大的数,找到所有情况
4.在最大的数左区间内,使用双指针,统计有效三角形个数
三.编写代码
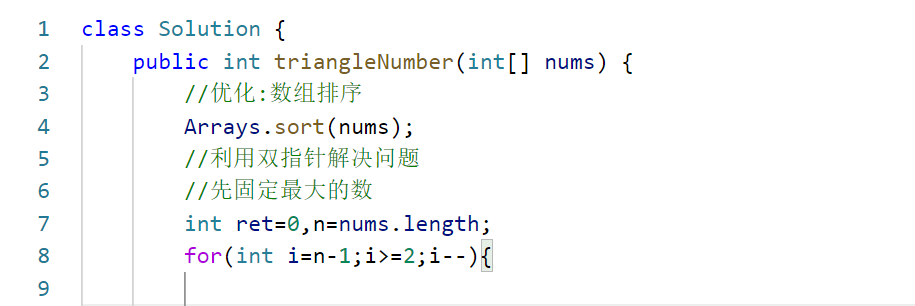
1.排序
2.固定最大的数
注意, i 为固定的最大的数,所以 i 指向最后的位置,数组内至少3个数,所以 i 最多最多走到第3个位置,对应到数组中 i >= 2
java
class Solution {
public int triangleNumber(int[] nums) {
//优化:数组排序
Arrays.sort(nums);
//利用双指针解决问题
//先固定最大的数
int ret=0,n=nums.length;
for(int i=n-1;i>=2;i--){//先固定最大的数
int left=0,right=i-1;
while(left<right){
if(nums[left]+nums[right]>nums[i]){
ret+=right-left;//注意是 +=
right--;//可以构成
}else{
left++;//无法构成
}
}
}
return ret;
}
}