数据结构排序算法详解（2）——选择排序（附动图）

星轨初途2025-11-26 12:40

文章目录

个人主页：星轨初途

个人专栏：C语言，数据结构



前言

嗨٩(๑❛ᴗ❛๑)۶，今天我们继续来了解排序，本篇来讲几种选择排序------直接选择排序和堆排序，让我们来了解他们吧！

四、选择排序

1、直接选择排序

（1）概念及实现

概念：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

我们可以通过这个图来更加清晰了解过程



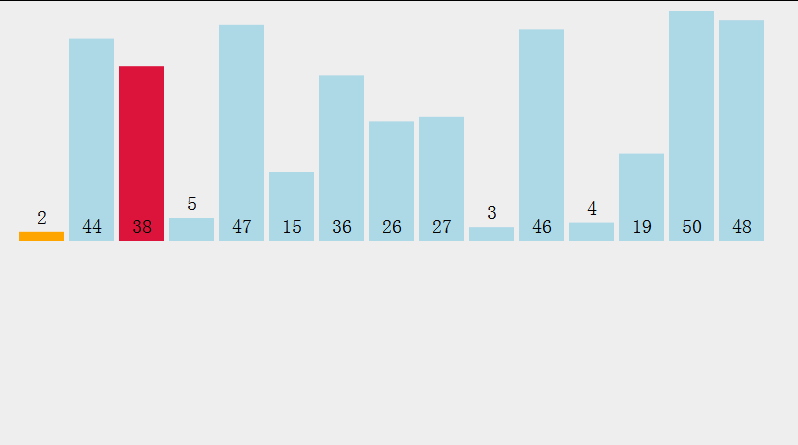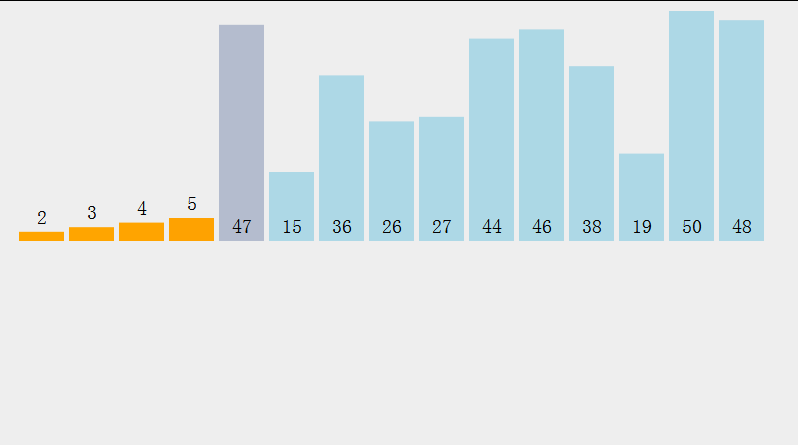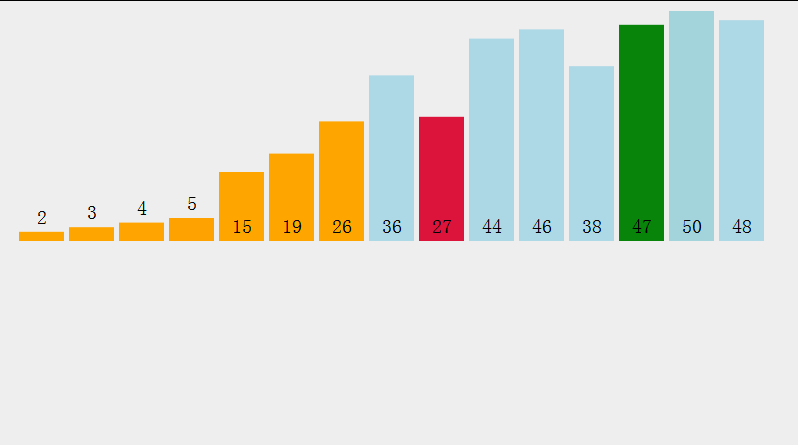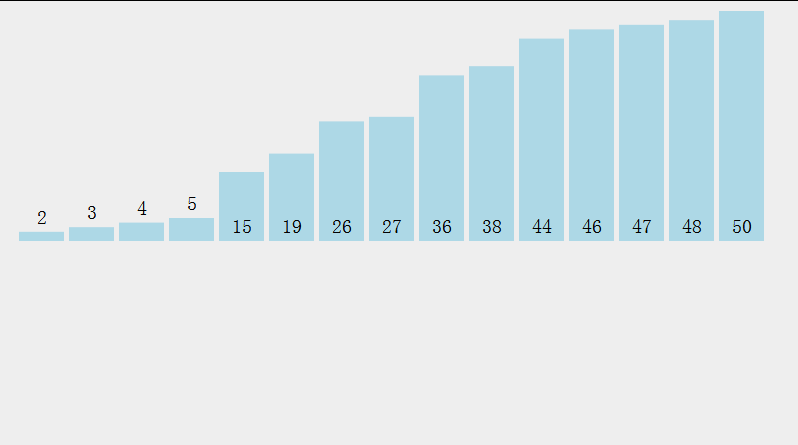
这样效率太低了，我们来稍微改变一下，同时找最小和最大的，最小和前面交换，最大与后面交换

我们这里先写一个交换函数

c 复制代码 
void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

再实现功能

c 复制代码 
void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void SelectSort(int* a, int n)
{
    int begin = 0, end = n - 1;

    while (begin < end)
    {
        int mini = begin, maxi = begin;
        for (int i = begin + 1; i <= end; ++i)
        {
            if (a[i] > a[maxi])
            {
                maxi = i;
            }

            if (a[i] < a[mini])
            {
                mini = i;
            }
        }

        Swap(&a[begin], &a[mini]);
        if (begin == maxi)
 			maxi = mini;
        Swap(&a[end], &a[maxi]);
        ++begin;
        --end;
    }
}

这里我们说一下下面这一段功能

c 复制代码 
if (begin == maxi)
 			maxi = mini;

防止最大值再开头，导致最小交换后，后面与最大交换，实际不是最大
测试：

c 复制代码 
int main()
{
    int arr[] = { 2,5,3,76,9,10,32,11,2 };
    PrintArray(arr, sizeof(arr) / sizeof(int));
    SelectSort(arr, sizeof(arr) / sizeof(int));
    PrintArray(arr, sizeof(arr) / sizeof(int));
   /* TestOP();*/
    return 0;
}

功能正常实现

（2）时间复杂度

这个一看就看出来了，遍历n/2次

优化版直接选择排序（同时找最大和最小值）的总比较次数为 ( n + (n-2) + (n-4) + ......)，近似为n2/2，仍属于 O(n2)量级。

（3）特性

1、直接选择排序思考虽然非常好理解，但是因为效率不是很好。实际中我们很少去使用；

2、时间复杂度：O(N ^ 2)；

3、空间复杂度：O(1)。

2、堆排序

（1）概念及实现

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。
需要注意的是排升序要建大堆，排降序建小堆。

我们前面专门讲过，这里就不过多讲解了
传送门《数据结构二叉树之堆 ------ 优先队列与排序的高效实现（2）》<-这一篇下面有

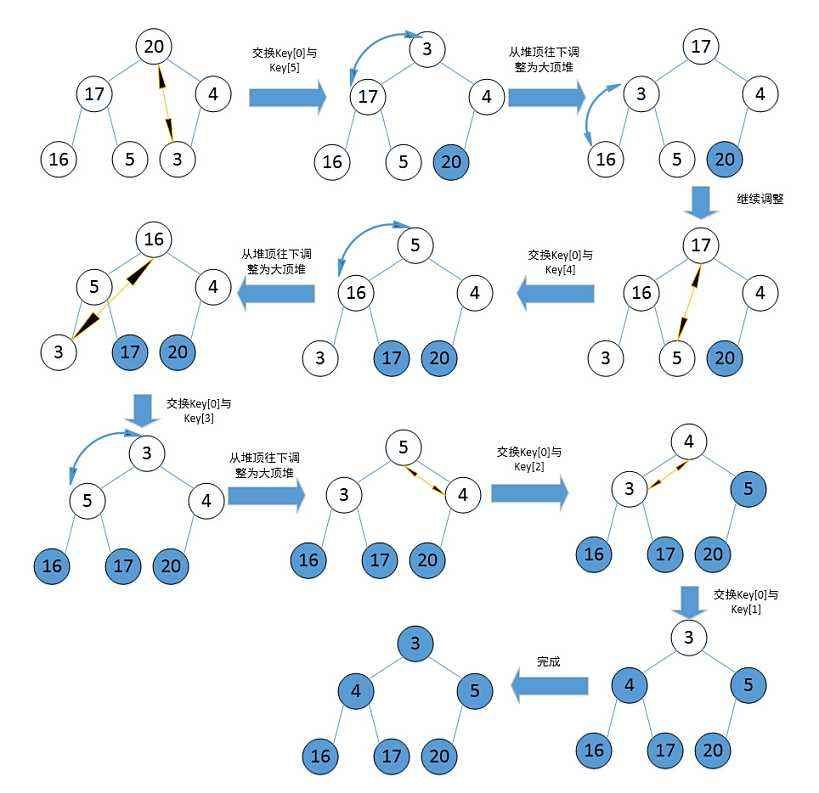
我们这里直接实现

先实现向下调整建堆，在实现堆排序

c 复制代码 
//向下调整建堆
void AdjustDown(int* a, int n, int parent)
{
    // 先假设左孩子小
    int child = parent * 2 + 1;

    while (child < n)  // child >= n说明孩子不存在，调整到叶子了
    {
        // 找出小的那个孩子
        if (child + 1 < n && a[child + 1] > a[child])
        {
            ++child;
        }

        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}
//堆排序
void HeapSort(int* a, int n)
{
    // 向下调整建堆 O(N)
    for (int i = (n - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, n, i);
    }

    // O(N*logN)
    int end = n - 1;
    while (end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        --end;
    }
}

测试

test.c

c 复制代码 
int main()
{
    int arr[] = { 2,5,3,76,9,10,32,11,2 };
    PrintArray(arr, sizeof(arr) / sizeof(int));
    HeapSort(arr, sizeof(arr) / sizeof(int));
    PrintArray(arr, sizeof(arr) / sizeof(int));
   /* TestOP();*/
    return 0;
}

正确实现

（2）时间复杂度

O（n*logn）
《数据结构二叉树之堆 ------ 优先队列与排序的高效实现（2）》

这一篇已经讲的很详细啦，这里就不做解释啦

（3）特性

  1. 时间复杂度稳定 O ( n log ⁡ n ) O(n \log n) O(nlogn)，空间复杂度 O ( 1 ) O(1) O(1)；
  2. 适合大规模数据排序，但小规模场景下缓存效率较低。
  3. 堆排序可用于Top-K问题（如找最大的k个元素），无需完全排序，效率更高，时间复杂度为 O ( n + k log ⁡ n ) O(n + k \log n) O(n+klogn)。
  4. 排升序要建大堆，排降序建小堆

3、对比插入排序和选择排序

我们这次对比插入排序和选择排序的所有排序

先来10万个数

test.c

c 复制代码 
#include"Sort.h"
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);/*
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);*/

	for (int i = 0; i < N; ++i)
	{
		// Öظ´²>>¶à
		a1[i] = rand() + i;
		// Öظ´½Ï¶à
		//a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		/*a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];*/
	}

	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	//PrintArray(a2, N);

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	//BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	/*printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);*/

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	/*free(a5);
	free(a6);
	free(a7);*/
}
int main()
{
    /*int arr[] = { 2,5,3,76,9,10,32,11,2 };
    PrintArray(arr, sizeof(arr) / sizeof(int));
    HeapSort(arr, sizeof(arr) / sizeof(int));
    PrintArray(arr, sizeof(arr) / sizeof(int));*/
    TestOP();
    return 0;
}

结果，我们可以看出希尔排序和堆排序都挺快的，插入有点慢，直接选择排序太慢了

4、总代码

Sort.h

c 复制代码 
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include <time.h>
//直接插入排序
void InsertSort(int* a, int n);
// O(N ^ 1.3)
//希尔排序
void ShellSort(int* a, int n);
//打印
void PrintArray(int* a, int n);
//交换
void Swap(int* p1, int* p2);
//直接选择排序
void SelectSort(int* a, int n);
//堆排序
void HeapSort(int* a, int n);
//向下调整建堆
void AdjustDown(int* a, int n, int parent);

Sort.c

c 复制代码 
#include"Sort.h"
//直接插入排序
void InsertSort(int* a, int n)
{
    //  [0, n-1]
    for (int i = 0; i < n - 1; i++)
    {
        // [0, n-2]是最后一组
        // [0,end]有序 end+1位置的值插入[0,end]，保持有序
        int end = i;
        int tmp = a[end + 1];
        while (end >= 0)
        {
            //升序大于>,降序小于
            if (tmp < a[end])
            {
                a[end + 1] = a[end];
                --end;
            }
            else
            {
                break;
            }
        }
        a[end + 1] = tmp;
    }
}
// O(N ^ 1.3)
//希尔排序
void ShellSort(int* a, int n)
{
    int gap = n;
    while (gap > 1)
    {
        // +1保证最后一个gap一定是1
        // gap > 1时是预排序
        // gap == 1时是插入排序
        gap = gap / 3 + 1;

        for (size_t i = 0; i < n - gap; ++i)
        {
            int end = i;
            int tmp = a[end + gap];
            while (end >= 0)
            {
                if (tmp < a[end])
                {
                    a[end + gap] = a[end];
                    end -= gap;
                }
                else
                {
                    break;
                }
            }
            a[end + gap] = tmp;
        }
    }
}
//打印
void PrintArray(int* a, int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
}
void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void SelectSort(int* a, int n)
{
    int begin = 0, end = n - 1;

    while (begin < end)
    {
        int mini = begin, maxi = begin;
        for (int i = begin + 1; i <= end; ++i)
        {
            if (a[i] > a[maxi])
            {
                maxi = i;
            }

            if (a[i] < a[mini])
            {
                mini = i;
            }
        }

        Swap(&a[begin], &a[mini]);
        if (begin == maxi)
            maxi = mini;
        Swap(&a[end], &a[maxi]);
        ++begin;
        --end;
    }
}
//向下调整建堆
void AdjustDown(int* a, int n, int parent)
{
    // 先假设左孩子小
    int child = parent * 2 + 1;

    while (child < n)  // child >= n说明孩子不存在，调整到叶子了
    {
        // 找出小的那个孩子
        if (child + 1 < n && a[child + 1] > a[child])
        {
            ++child;
        }

        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}
//堆排序
void HeapSort(int* a, int n)
{
    // 向下调整建堆 O(N)
    for (int i = (n - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDown(a, n, i);
    }

    // O(N*logN)
    int end = n - 1;
    while (end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDown(a, end, 0);
        --end;
    }
}

test.c

c 复制代码 
#define _CRT_SECURE_NO_WARNINGS 1
#include"Sort.h"
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);/*
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);*/

	for (int i = 0; i < N; ++i)
	{
		// Öظ´²>>¶à
		a1[i] = rand() + i;
		// Öظ´½Ï¶à
		//a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		/*a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];*/
	}

	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	//PrintArray(a2, N);

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	//BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	/*printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);*/

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	/*free(a5);
	free(a6);
	free(a7);*/
}
int main()
{
    /*int arr[] = { 2,5,3,76,9,10,32,11,2 };
    PrintArray(arr, sizeof(arr) / sizeof(int));
    HeapSort(arr, sizeof(arr) / sizeof(int));
    PrintArray(arr, sizeof(arr) / sizeof(int));*/
    TestOP();
    return 0;
}

结束语

嗨ヾ(◍°∇°◍)ﾉﾞ！本篇到这里就结束啦！本篇对选择排序进行实现，并对比选择排序和插入排序的性能，下一篇我们将要接触------交换排序，下一篇将要花大量篇幅讲其中的快排，敬请期待吧！（我也挺期待的(◕ᴗ◕✿)）让我们下一篇再见吧！

相关知识传送门：
《数据结构二叉树之堆 ------ 优先队列与排序的高效实现（2）》
数据结构排序算法详解（1）------介绍及插入排序（附动图

往期回顾
算法的时间复杂度和空间复杂度
栈与队列核心篇（上）：从原理到代码，吃透栈结构
栈与队列核心篇（下）：从基础到进阶，玩转队列设计
数据结构核心：栈 / 队列互转 + 循环队列，三大必刷题型深度拆解
函数的栈帧的创建和销毁（超详细版本图文丰富）
数据结构之初识二叉树（1）------核心概念入门
《数据结构二叉树之堆 ------ 优先队列与排序的高效实现（2）》
《数据结构二叉树之堆 ------ 优先队列与排序的高效实现（2）（下）》
数据结构二叉树之链式结构（3）（上）
数据结构二叉树之链式结构（3）（下）
数据结构二叉树应用实战：多场景练习题强化巩固
数据结构排序算法详解（1）------介绍及插入排序（附动图

相关推荐
合作小小程序员小小店29 分钟前
游戏开发，桌面%小游戏，俄罗斯方块%demo，基于vs2022,c语言,背景音乐,easyX,无数据库,
c语言·开发语言
kaikaile19952 小时前
基于 MATLAB 的室内三维定位
算法
雾岛听蓝2 小时前
C++ 入门核心知识点（从 C 过渡到 C++ 基础）
开发语言·c++·经验分享·visual studio
AGI前沿2 小时前
AdamW的继任者？AdamHD让LLM训练提速15%，性能提升4.7%，显存再省30%
人工智能·算法·语言模型·aigc
Tan_Ying_Y2 小时前
什么是垃圾回收算法 他的底层原理是什么？
算法
EXtreme352 小时前
【C 语言专栏收官】预处理完全攻略：宏、条件编译与代码安全的最后一道防线
c语言·预处理·宏
Xの哲學2 小时前
Linux 分区表深度技术剖析
linux·网络·算法·架构·边缘计算
jiushun_suanli2 小时前
量子纠缠：颠覆认知的宇宙密码
经验分享·学习·量子计算
写写闲篇儿2 小时前
经典算法题剖析之传递信息（三）
算法
热门推荐
01GitHub 镜像站点02【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连03BongoCat - 跨平台键盘猫动画工具04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Google Antigravity：无法登录？早期错误、登录修复和用户反馈指南07Linux下V2Ray安装配置指南08全球最强模型Grok4，国内已可免费使用！（附教程）09Labelme从安装到标注：零基础完整指南10Spring Boot 4.0 发布总结：新特性、依赖变更与升级指南