INT305 Machine Learning 机器学习 Pt.4

文章目录

• [1. 二元分类](#1. 二元分类)
• • [1.1 线性模型](#1.1 线性模型)
  • [1.2 0-1损失函数](#1.2 0-1损失函数)
  • [1.3 几何方法解决二元分类](#1.3 几何方法解决二元分类)
  • • [1.3.1 分隔超平面（Separating Hyperplanes）](#1.3.1 分隔超平面（Separating Hyperplanes）)
    • [1.3.2 最优分隔超平面（Optimal Separating Hyperplane）](#1.3.2 最优分隔超平面（Optimal Separating Hyperplane）)
    • [1.3.3 非线性可分](#1.3.3 非线性可分)
    • • [1.3.3.1 软间隔（Soft Margin）](#1.3.3.1 软间隔（Soft Margin）)
      • [1.3.3.2 合页损失（Hinge Loss）](#1.3.3.2 合页损失（Hinge Loss）)
• [2. 多类分类](#2. 多类分类)
• • [2.1 多类支持向量机（Multiclass SVM）](#2.1 多类支持向量机（Multiclass SVM）)
  • [2.2 Softmax分类器（多项式逻辑回归）](#2.2 Softmax分类器（多项式逻辑回归）)
  • [2.3 总结](#2.3 总结)

1. 二元分类

1.1 线性模型

在二元分类中，线性模型通常使用以下公式来预测输出：
z = w ⊤ x + b z = \mathbf{w}^\top \mathbf{x} + b z=w⊤x+b：这是一个线性方程，其中 w w w是权重向量， x x x是输入特征向量， b b b是偏置项， ⊤ ⊤ ⊤表示向量的转置。这个方程计算了一个线性组合，得到一个标量 z z z。
y = sign ( z ) y = \text{sign}(z) y=sign(z)：这个方程使用符号函数（sign function）来将 z z z的值转换为 -1 或 +1。如果 z z z是正数， y y y将是 +1；如果 z z z是负数， y y y将是 -1。

但是如何确定权重向量 w w w和偏置项 b b b呢？在实际应用中，这通常通过训练数据来完成，使用优化算法（如梯度下降）来最小化损失函数，从而找到最佳的 w w w和 b b b值。

1.2 0-1损失函数

这是一种简单的损失函数，用于衡量模型预测 y y y与真实标签 t t t之间的差异。
L 0 − 1 ( y , t ) = { 0 if y = t 1 if y ≠ t \mathcal{L}_{0-1}(y, t) = \begin{cases} 0 & \text{if } y = t \\ 1 & \text{if } y \neq t \end{cases} L0−1(y,t)={01if y=tif y=t

也可以表示为：
L 0 − 1 ( y , t ) = I { y ≠ t } \mathcal{L}_{0-1}(y, t) = \mathbb{I}\{y \neq t\} L0−1(y,t)=I{y=t}

其中， I \mathbb{I} I是指示函数（Indicator Function），当条件成立时取值为1，否则为0。

它有两点局限性：

1. 计算困难：直接最小化0-1损失函数在计算上是非常困难的，因为它是一个非连续的函数，不适用于梯度下降等优化算法。
2. 无法区分不同假设：0-1损失函数无法区分那些达到相同准确率的不同假设。这意味着即使不同的模型参数组合在预测结果上表现相同，0-1损失函数也无法区分它们。

因此为了解决0-1损失函数的局限性，研究者们探索了其他更容易最小化的损失函数，例如逻辑回归中的交叉熵损失（Cross-Entropy Loss） L C E \mathcal{L}_{CE} LCE。也可以从二元分类器的几何特性出发，探索不同的方法来解决这些问题。

1.3 几何方法解决二元分类

1.3.1 分隔超平面（Separating Hyperplanes）

我们可以尝试在特征空间中找到一个线性边界（超平面），将不同类别的数据点分开。

在二维空间中，这个边界是一条直线；在三维空间中，它是一个平面；在更高维空间中，它被称为超平面。

例如现在我们有两组数据点，一组用红色圆点表示，另一组用蓝色星号表示。

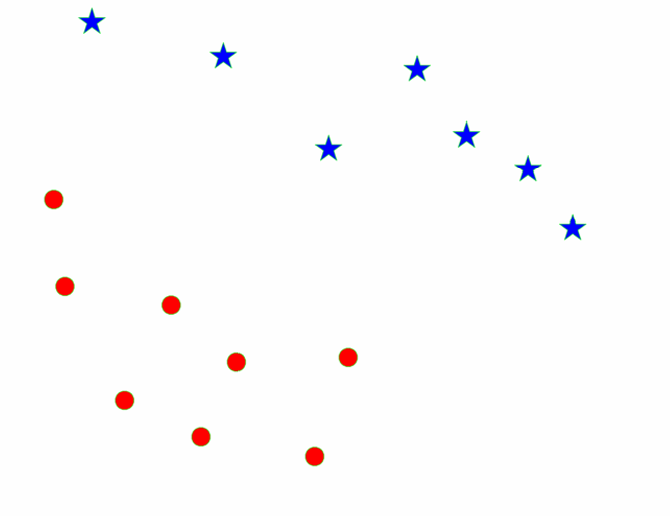
这些点代表两个不同的类别，我们现在尝试找到一个线性分类器（如超平面），能够将这两组点完全分开。

​

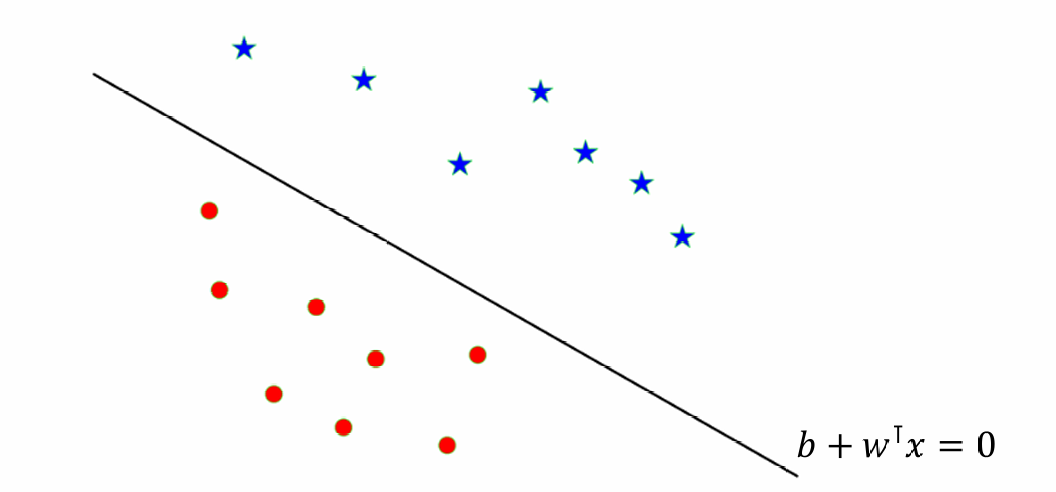
在这个例子中决策边界看起来像一条线，但在更高维空间中，它是一个 D − 1 D−1 D−1维的超平面。

超平面是由满足方程 f ( x ) = w ⊤ x + b = 0 f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b = 0 f(x)=w⊤x+b=0的点 x x x组成的集合。

这个式子正是我们前面线性模型的输出值 z z z的式子： z = w ⊤ x + b z = \mathbf{w}^\top \mathbf{x} + b z=w⊤x+b，前面我们还使用符号函数 y y y来确定分类结果。如果 z > 0 z>0 z>0，则 y = + 1 y=+1 y=+1；如果 z < 0 z<0 z<0，则 y = − 1 y=−1 y=−1；而 z = 0 z=0 z=0正好是分界线，这里 y y y可以是 +1 或 -1，具体取决于实现和数据集的标签约定。

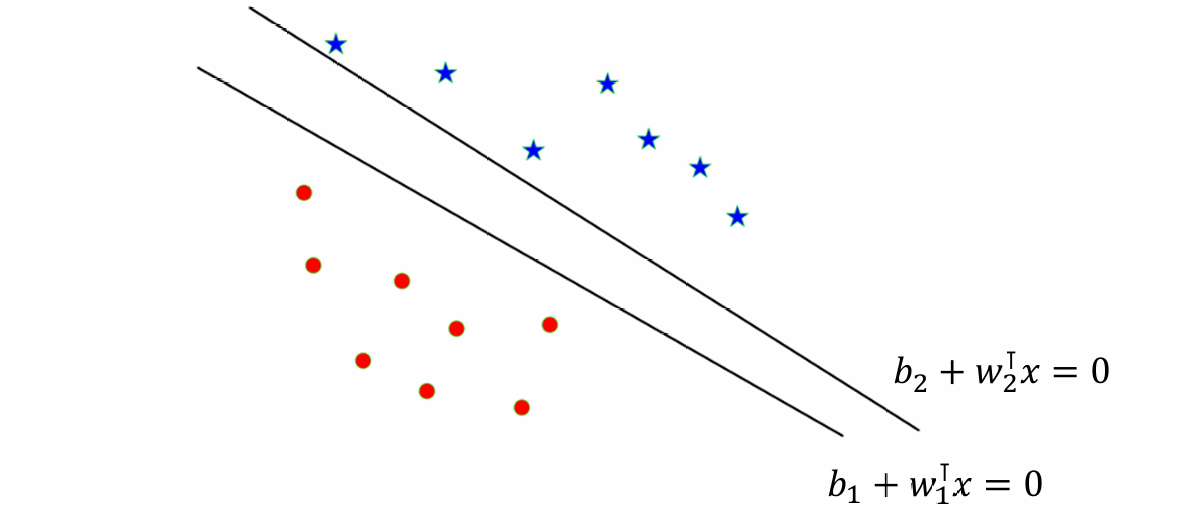
当然我们这里存在多个可以分隔两个类别数据点的超平面，这些超平面有不同的权重向量和偏置项 ( w , b ) ( \mathbf{w},b) (w,b)。

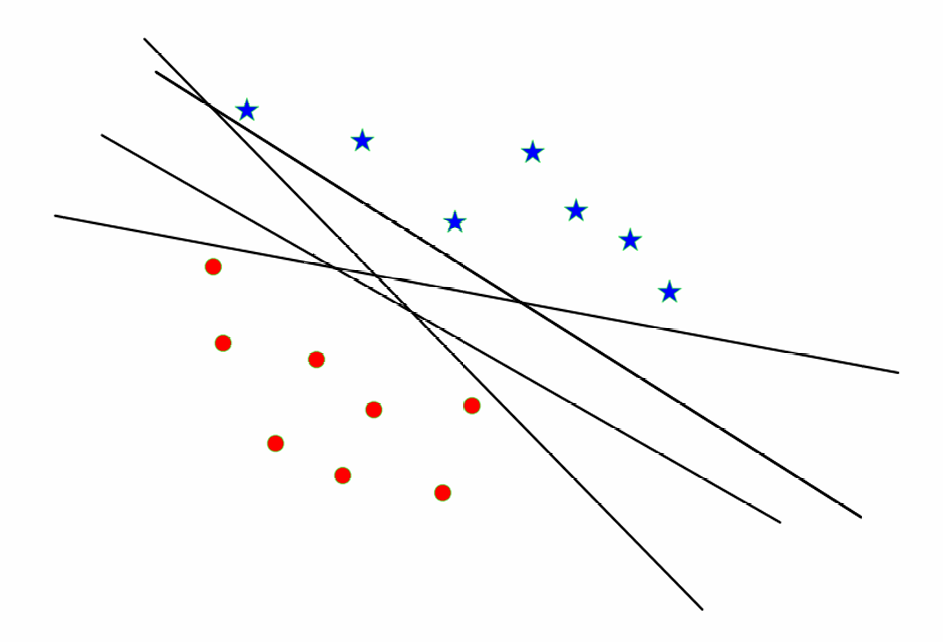
由于这样的超平面有很多，因此在实际应用中，我们通常希望选择一个最优的超平面，以最大化不同类别之间的间隔（边距）。

1.3.2 最优分隔超平面（Optimal Separating Hyperplane）

最优分隔超平面是指能够将两个类别的数据点完全分开，并且最大化到任一类最近点的距离的超平面。这个距离也被称为分类器的间隔（margin）。

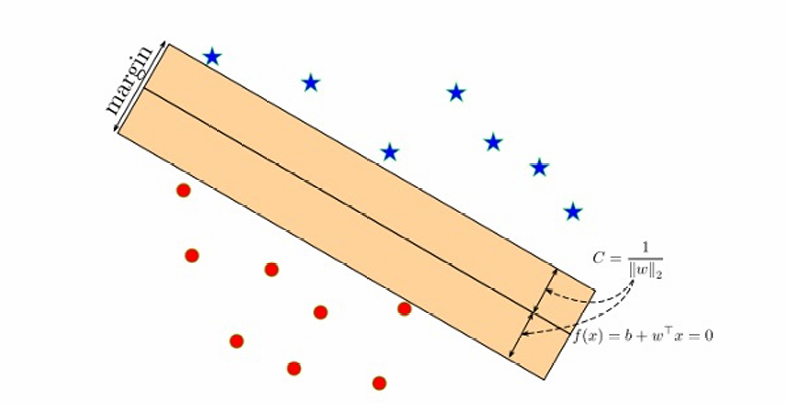
如图所示，中间的黑线是分隔这两个类别的最优超平面，这条线距离这两个类别最近点的距离是一样的，因此间隔（margin）是这个距离的两倍。

超平面的方程依然是： f ( x ) = w ⊤ x + b = 0 f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b = 0 f(x)=w⊤x+b=0

边距 C C C定义为： C = 1 ∥ w ∥ 2 C = \frac{1}{\|\mathbf{w}\|_2} C=∥w∥21，其中 ∥ w ∥ 2 {\|\mathbf{w}\|_2} ∥w∥2是权重向量 w \mathbf{w} w的L2范数（欧几里得范数）。

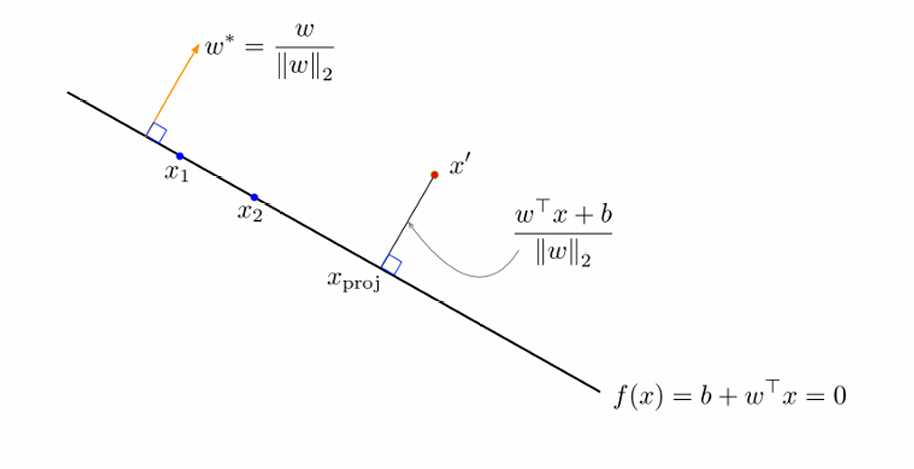
决策超平面与 w \mathbf{w} w正交（垂直）。
w ∗ \mathbf{w}^* w∗是一个单位向量，指向与 w \mathbf{w} w相同的方向。

因此同一个超平面可以用 w ∗ \mathbf{w}^* w∗来等价定义，因为 w ∗ \mathbf{w}^* w∗保持了 w \mathbf{w} w的方向，只是长度为1。

我们可以计算一个点到超平面的垂直距离，如图所示，点 x ′ x^′ x′到超平面的 w ⊤ x ′ + b ∥ w ∥ 2 \frac{\mathbf{w}^\top \mathbf{x^′} + b}{\|\mathbf{w}\|_2} ∥w∥2w⊤x′+b

对于第 i i i个数据点，当且仅当 sign ( w ⊤ x ( i ) + b ) = t ( i ) \text{sign}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) = t^{(i)} sign(w⊤x(i)+b)=t(i)时，分类是正确的。这里， w \mathbf{w} w是权重向量， x ( i ) x^(i) x(i)是第 i i i个数据点， b b b是偏置项， t ( i ) t^(i) t(i)是该点的真实标签。

上述等式可以重写为不等式形式： t ( i ) ( w ⊤ x ( i ) + b ) > 0 t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) > 0 t(i)(w⊤x(i)+b)>0，也就是必须输出值与标签 t ( i ) t^{(i)} t(i)同号

为了强制执行一个间隔 C C C，我们进一步要求： t ( i ) ⋅ ( w ⊤ x ( i ) + b ) ∥ w ∥ 2 ≥ C t^{(i)} \cdot \frac{(\mathbf{w}^\top \mathbf{x}^{(i)} + b)}{\|\mathbf{w}\|_2} \geq C t(i)⋅∥w∥2(w⊤x(i)+b)≥C，这个条件确保了所有数据点到决策边界的距离至少为 C C C。

因此我们现在的问题转化为了最大化间隔 C C C，我们要将这个问题转化为一个优化问题。

优化问题可以表示为： max ⁡ w , b C \max_{\mathbf{w}, b} C maxw,bC

约束条件是： t ( i ) ( w ⊤ x ( i ) + b ) ∥ w ∥ 2 ≥ C for i = 1 , ... , N \frac{t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)}{\|\mathbf{w}\|_2} \geq C \quad \text{for } i = 1, \ldots, N ∥w∥2t(i)(w⊤x(i)+b)≥Cfor i=1,...,N，其中 N N N是数据点的数量。

通过将 C = 1 ∥ w ∥ 2 C=\frac{1}{\|\mathbf{w}\|_2} C=∥w∥21代入约束条件，可以得到： t ( i ) ( w ⊤ x ( i ) + b ) ∥ w ∥ 2 ≥ 1 ∥ w ∥ 2 \frac{t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)}{\|\mathbf{w}\|_2} \geq \frac{1}{\|\mathbf{w}\|_2} ∥w∥2t(i)(w⊤x(i)+b)≥∥w∥21

这可以进一步简化为： t ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 for i = 1 , ... , N t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) \geq 1 \quad \text{for } i = 1, \ldots, N t(i)(w⊤x(i)+b)≥1for i=1,...,N这个约束条件被称为代数间隔约束（algebraic margin constraint）。前面的约束条件可以被称为几何代数间隔约束（geometric margin constraint）。

因此，等价的优化问题可以表示为： min ⁡ w ∥ w ∥ 2 2 \min_{\mathbf{w}} \|\mathbf{w}\|_2^2 minw∥w∥22

约束条件仍然是： t ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 for i = 1 , ... , N t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) \geq 1 \quad \text{for } i = 1, \ldots, N t(i)(w⊤x(i)+b)≥1for i=1,...,N，因为 C C C是 ∥ w ∥ 2 {\|\mathbf{w}\|_2} ∥w∥2的倒数( C = 1 ∥ w ∥ 2 C=\frac{1}{\|\mathbf{w}\|_2} C=∥w∥21)。

我们观察可发现有的数据点 x ( i ) x^{(i)} x(i)的间隔约束不是紧的(tight)，即不满足 t ( i ) ( w ⊤ x ( i ) + b ) = 1 t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) = 1 t(i)(w⊤x(i)+b)=1，那么可以从训练集中移除这个点，而不会改变最优的 w \mathbf{w} w。

重要的训练样本是那些满足 t ( i ) ( w ⊤ x ( i ) + b ) = 1 t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) = 1 t(i)(w⊤x(i)+b)=1的点，这些点被称为支持向量。这些点位于间隔边界上，即它们到超平面的距离正好等于间隔的一半。

因此这个算法被称为（硬）支持向量机（SVM）或支持向量分类器。

类似于SVM的算法通常被称为最大间隔或大间隔算法。

1.3.3 非线性可分

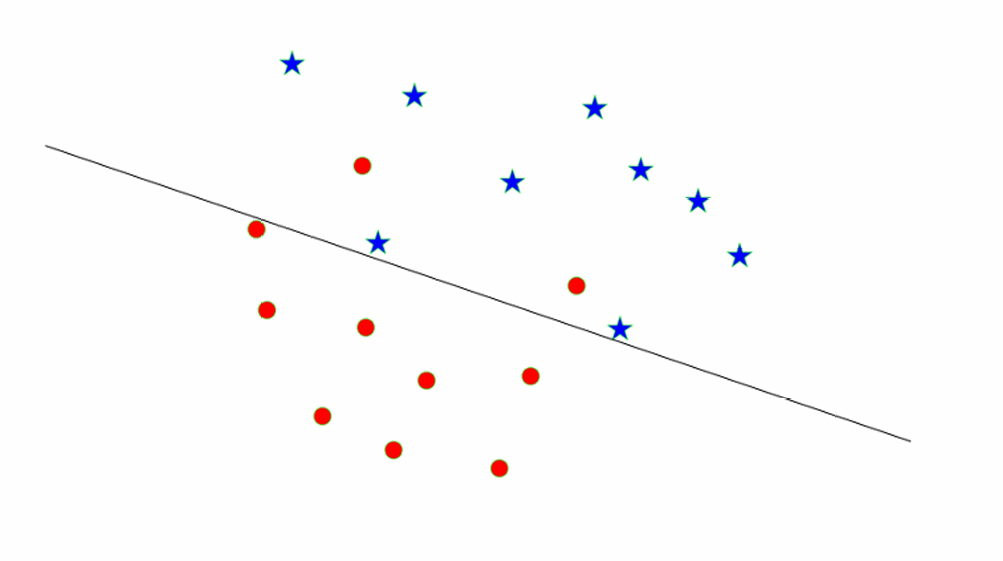
上图展示的例子很明显我们无法直接用一条线将两组数据分开。

解决方案一般有三种：

1. 核技巧（Kernel Trick）。核技巧通过将数据映射到一个更高维的特征空间，在该空间中数据可能变得线性可分。
2. 软间隔（Soft Margin）。在实际应用中，即使数据在原始空间中线性可分，引入一些松弛变量（slack variables）来允许一些数据点违反间隔约束，也可以帮助模型更好地泛化。
3. 正则化。通过在损失函数中添加权重向量的正则化项（如L2正则化），可以控制模型的复杂度，防止过拟合。

1.3.3.1 软间隔（Soft Margin）

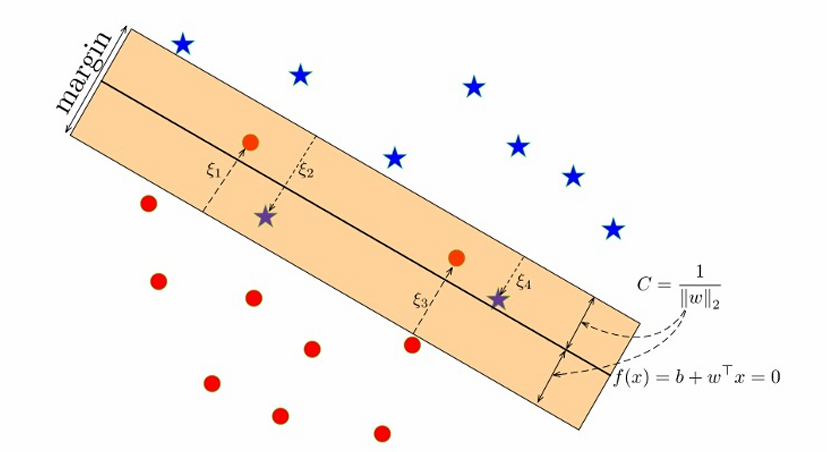
在软间隔SVM中，允许一些数据点位于间隔内或甚至被错误分类。这是通过引入松弛变量 ξ i ξ_i ξi来实现的，这些变量表示每个数据点违反间隔约束的程度。

松弛变量 ξ i ξ_i ξi用于表示第 i i i个数据点到决策边界的距离。如果 ξ i > 0 ξ_i >0 ξi>0，则表示在间隔内或被错误分类。

软间隔SVM的优化目标是最小化以下函数： min ⁡ w , b , ξ ( 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i ) \min_{\mathbf{w}, b, \xi} \left( \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^N \xi_i \right) minw,b,ξ(21∥w∥2+C∑i=1Nξi)其中， C C C是一个正则化参数，用于控制间隔最大化和分类错误之间的权衡，不是前面的表示间隔大小的 C C C。

约束条件是： t ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 − ξ i for i = 1 , ... , N t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) \geq 1 - \xi_i \quad \text{for } i = 1, \ldots, N t(i)(w⊤x(i)+b)≥1−ξifor i=1,...,N
ξ i ≥ 0 for i = 1 , ... , N \xi_i \geq 0 \quad \text{for } i = 1, \ldots, N ξi≥0for i=1,...,N

这些约束条件确保所有数据点至少满足 t ( i ) ( w ⊤ x ( i ) + b ) = 1 t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) = 1 t(i)(w⊤x(i)+b)=1的条件，除非它们有非零的松弛变量 ξ i ξ_i ξi。

软间隔SVM（soft-margin SVM）的约束条件： ∥ w ∥ 2 t ( i ) ( w ⊤ x ( i ) + b ) ≥ C ( 1 − ξ i ) \frac{\|\mathbf{w}\|_2}{t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)} \geq C(1 - \xi_i) t(i)(w⊤x(i)+b)∥w∥2≥C(1−ξi)

需要对所有数据点的松弛变量 ξ i ξ_i ξi进行惩罚，以控制分类错误的数量。这通常通过在优化目标中添加一个与 ξ i ξ_i ξi相关的项来实现。

软间隔SVM的优化目标是： min ⁡ w , b , ξ ( 1 2 ∥ w ∥ 2 + γ ∑ i = 1 N ξ i ) \min_{\mathbf{w}, b, \xi} \left( \frac{1}{2} \|\mathbf{w}\|^2 + \gamma \sum_{i=1}^N \xi_i \right) minw,b,ξ(21∥w∥2+γ∑i=1Nξi)

这里惩罚程度的参数 γ γ γ是一个超参数，它控制模型对间隔和分类错误的权衡。

当 γ = 0 γ=0 γ=0时，模型不关心分类错误，只关注间隔最大化，这会导致 w=0。

当 γ → ∞ γ→∞ γ→∞时，模型只关注分类正确性，忽略间隔，这相当于硬间隔SVM（hard-margin SVM）。

其中， γ γ γ是一个超参数，用于权衡间隔最大化和分类错误之间的权衡。

也可以通过约束 ∑ i = 1 N ξ i \sum_{i=1}^N \xi_i ∑i=1Nξi而不是惩罚 ∑ i = 1 N ξ i \sum_{i=1}^N \xi_i ∑i=1Nξi来实现软间隔。

1.3.3.2 合页损失（Hinge Loss）

合页损失是软间隔SVM约束条件所推导出来的损失函数，，用于衡量模型在分类任务中的表现。

我们现在看到前面软间隔SVM的约束条件是： t ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 − ξ i for i = 1 , ... , N t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) \geq 1 - \xi_i \quad \text{for } i = 1, \ldots, N t(i)(w⊤x(i)+b)≥1−ξifor i=1,...,N
ξ i ≥ 0 for i = 1 , ... , N \xi_i \geq 0 \quad \text{for } i = 1, \ldots, N ξi≥0for i=1,...,N

这个约束可以重写为： ξ i ≥ 1 − t ( i ) ( w ⊤ x ( i ) + b ) \xi_i \geq 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) ξi≥1−t(i)(w⊤x(i)+b)这意味着 ξ i ξ_i ξi表示每个数据点违反间隔约束的程度。

情况1：如果 1 − t ( i ) ( w ⊤ x ( i ) + b ) ≤ 0 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) \leq 0 1−t(i)(w⊤x(i)+b)≤0，则最小的非负 ξ i ξ_i ξi满足约束是 ξ i = 0 ξ_i=0 ξi=0。

情况2：如果 1 − t ( i ) ( w ⊤ x ( i ) + b ) > 0 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) > 0 1−t(i)(w⊤x(i)+b)>0，则最小的非负 ξ i ξ_i ξi满足约束是 ξ i = 1 − t ( i ) ( w ⊤ x ( i ) + b ) \xi_i = 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) ξi=1−t(i)(w⊤x(i)+b)。

因此， ξ i = max ⁡ { 0 , 1 − t ( i ) ( w ⊤ x ( i ) + b ) } \xi_i = \max\{0, 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)\} ξi=max{0,1−t(i)(w⊤x(i)+b)}.

合页损失可以表示为所有数据点的松弛变量之和： ∑ i = 1 N ξ i = ∑ i = 1 N max ⁡ { 0 , 1 − t ( i ) ( w ⊤ x ( i ) + b ) } \sum_{i=1}^N \xi_i = \sum_{i=1}^N \max\{0, 1 - t^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)\} ∑i=1Nξi=∑i=1Nmax{0,1−t(i)(w⊤x(i)+b)}

如果我们将模型的预测表示为 y ( i ) ( w , b ) = w ⊤ x + b y^{(i)}(\mathbf{w},b)=\mathbf{w}^⊤\mathbf{x}+b y(i)(w,b)=w⊤x+b，那么软间隔SVM的优化问题可以写为： min ⁡ w , b , ξ ∑ i = 1 N max ⁡ { 0 , 1 − t ( i ) y ( i ) ( w , b ) } + 1 2 γ ∥ w ∥ 2 2 \min_{\mathbf{w}, b, \xi} \sum_{i=1}^{N} \max\{0, 1 - t^{(i)} y^{(i)}(\mathbf{w}, b)\} + \frac{1}{2\gamma} \|\mathbf{w}\|_2^2 minw,b,ξ∑i=1Nmax{0,1−t(i)y(i)(w,b)}+2γ1∥w∥22E，这里， γ γ γ是一个超参数，用于控制间隔最大化和分类错误最小化之间的权衡。

损失函数 L H ( y , t ) = max ⁡ { 0 , 1 − t y } \mathcal{L}_H(y, t) = \max\{0, 1 - ty\} LH(y,t)=max{0,1−ty}被称为合页损失。它衡量了模型预测 y 与实际标签 t 之间的差距，特别是当预测错误或模型对某些点的置信度不够时。

优化问题中的第二项 1 2 γ ∥ w ∥ 2 2 \frac{1}{2\gamma} \|\mathbf{w}\|_2^2 2γ1∥w∥22是权重向量 w \mathbf{w} w的 L 2 L_2 L2-范数（欧几里得范数）的平方。这一项用于正则化，防止模型过拟合。

因此，软间隔SVM可以被看作是一个线性分类器，它使用合页损失和 L 2 L_2 L2正则化项来优化模型。这种组合有助于提高模型的泛化能力，同时允许一定的分类错误。

2. 多类分类

2.1 多类支持向量机（Multiclass SVM）

在多类分类问题中，目标是为每个类别找到一个超平面，使得各类别之间的间隔最大化。

假设有三个训练示例，对应三个类别：猫（cat）、汽车（car）和青蛙（frog）。

这里， ( x i , y i ) (x_i ,y_i) (xi,yi)表示一个训练样本，其中 x i x_i xi是输入数据， y i y_i yi是对应的标签（或类别）。

我们可以使用使用权重矩阵 W W W和输入特征向量 x x x计算每个类别的分数 f ( x , W ) = W x f(x,W)=Wx f(x,W)=Wx。

多类SVM的损失函数定义为： L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) Li=∑j=yimax(0,sj−syi+1)其中 s = f ( x i , W ) = W x s=f(x_i,W)=Wx s=f(xi,W)=Wx是分数向量， s y i s_{y_i} syi是正确类别的分数， s y j s_{y_j} syj是其他类别的分数。

对于猫的图片，正确类别的分数是3.2，其他类别的分数分别是1.3（汽车）和2.2（青蛙）。
L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) Li=∑j=yimax(0,sj−syi+1)
= max ⁡ ( 0 , 5.1 − 3.2 + 1 ) + max ⁡ ( 0 , − 1.7 − 3.2 + 1 ) = \max(0, 5.1 - 3.2 + 1)+ \max(0, -1.7 - 3.2 + 1) =max(0,5.1−3.2+1)+max(0,−1.7−3.2+1)
= max ⁡ ( 0 , 2.9 ) + max ⁡ ( 0 , − 3.9 ) = \max(0, 2.9) + \max(0, -3.9) =max(0,2.9)+max(0,−3.9)
= 2.9 + 0 = 2.9 + 0 =2.9+0
= 2.9 = 2.9 =2.9

同理，对于汽车的照片。
L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) Li=∑j=yimax(0,sj−syi+1)
= max ⁡ ( 0 , 1.3 − 4.9 + 1 ) + max ⁡ ( 0 , − 2.0 − 4.9 + 1 ) = \max(0, 1.3 - 4.9 + 1)+ \max(0, -2.0 - 4.9 + 1) =max(0,1.3−4.9+1)+max(0,−2.0−4.9+1)
= max ⁡ ( 0 , − 2.6 ) + max ⁡ ( 0 , − 1.9 ) = \max(0, -2.6) + \max(0, -1.9) =max(0,−2.6)+max(0,−1.9)
= 0 + 0 = 0 + 0 =0+0
= 0 = 0 =0

同理，对于青蛙的照片。
L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1) Li=∑j=yimax(0,sj−syi+1)
= max ⁡ ( 0 , 2.2 − ( − 3.1 ) + 1 ) + max ⁡ ( 0 , 2.2 − ( − 3.1 ) + 1 ) = \max(0, 2.2 - (-3.1) + 1)+ \max(0, 2.2 - (-3.1) + 1) =max(0,2.2−(−3.1)+1)+max(0,2.2−(−3.1)+1)
= max ⁡ ( 0 , 6.3 ) + max ⁡ ( 0 , 6.6 ) = \max(0, 6.3) + \max(0, 6.6) =max(0,6.3)+max(0,6.6)
= 6.3 + 6.6 = 6.3 + 6.6 =6.3+6.6
= 12.9 = 12.9 =12.9

整个训练集的平均损失是所有样本损失的平均值：

平均损失 L L L的计算公式：
L = 1 N ∑ i = 1 N L i L = \frac{1}{N} \sum_{i=1}^{N} L_i L=N1∑i=1NLi

因此这个例子平均损失 L L L：
L = 2.9 + 0 + 12.9 3 = 5.27 L = \frac{2.9 + 0 + 12.9}{3} = 5.27 L=32.9+0+12.9=5.27

现在我们提出五个问题：

1. 如果求和是针对所有类别（包括 j = y i j=y_i j=yi）怎么办？

   这个问题是在探讨如果损失函数的求和包括了正确类别本身，即 j = y i j=y_i j=yi，会发生什么。

   在标准的多类SVM损失函数中，求和是针对所有非正确类别的 j j j进行的，即 j ≠ y i j\neq y_i j=yi ​。这是因为我们只关心模型对错误类别的预测是否过于自信，从而违反了间隔约束。

   如果包括正确类别 j = y i j=y_i j=yi在内，那么损失函数将计算正确类别的分数与自身的差值，这在逻辑上是没有意义的，因为正确类别的分数应该总是大于或等于其他所有类别的分数（至少满足间隔约束）。

2. 如果我们在这里使用平均值而不是求和怎么办？

   在标准的多类SVM损失函数中，损失是通过对所有非正确类别的分数进行求和来计算的。这种求和操作有助于强调模型对错误类别的预测错误。

   如果改为使用平均值，损失函数将计算所有非正确类别分数的平均损失。这可能会改变模型的学习动态，因为它将对每个错误类别的预测错误赋予相同的权重，而不是强调最大的预测错误。

3. 如果我们使用平方而不是求和，会发生什么？

   如果使用平方，损失函数将计算所有非正确类别的分数与正确类别分数之差的平方的最大值之和：
   L i = ∑ j ≠ y i max ⁡ ( 0 , s j − s y i + 1 ) 2 L_i = \sum_{j \neq y_i} \max(0, s_j - s_{y_i} + 1)^2 Li=∑j=yimax(0,sj−syi+1)2

   这种变化可能会增加对大误差的惩罚，从而影响模型的学习动态和最终的分类性能。

4. 多类支持向量机（SVM）损失函数可能的最小值和最大值是多少？

   最小值：对于多类SVM，这意味着对于每个样本，正确类别的分数 s y i s_{y_i} syi正好比所有其他类别的分数 s j s_{j} sj至少高1，因此 max ⁡ ( 0 , s j − s y i + 1 ) \max(0, s_j - s_{y_i} + 1) max(0,sj−syi+1)项将为0,从而整个损失为0。

   最大值： 理论上无穷大，这主要取决于错误类别分数 s j s_{j} sj与正确类别的分数 s y i s_{y_i} syi之间的相对关系。

5. 通常在初始化时 W W W是较小的数值，所以所有的 s ≈ 0 s≈0 s≈0。这种情况下的损失是多少？

   如果 W W W的初始值很小，那么通过 W W W计算得到的分数 s s s 也将接近于0，因此我们可以当作这里 s j ≈ 0 s_{j}≈0 sj≈0， s y i ≈ 0 s_{y_i}≈0 syi≈0，可以得到这里的值就是 C − 1 C-1 C−1（因为每一项都是1），这里 C C C代表类别数。

2.2 Softmax分类器（多项式逻辑回归）

Softmax分类器是一种将线性模型的输出转换为概率分布的方法，适用于多类分类问题。

给定一个输入图像 x i x_i xi和权重矩阵 W W W，首先计算分数向量 s = f ( x i ; W ) s=f(x_i ;W) s=f(xi;W)。

Softmax函数将这些未归一化的对数概率转换为归一化的概率分布，使得所有类别的概率之和为1。

Softmax函数的公式为：
P ( Y = k ∣ X = x i ) = e s k ∑ j e s j P(Y = k|X = \mathbf{x}i) = \frac{e^{s_k}}{\sum{j} e^{s_j}} P(Y=k∣X=xi)=∑jesjesk

其中 s k s_k sk是第 k k k类别的分数， s j s_j sj是所有类别的分数。

为了训练模型，我们希望最大化正确类别的对数概率的对数似然（log likelihood），或者等价地，最小化正确类别的负对数似然。

损失函数 L i L_i Li（交叉熵损失函数）定义为：
L i = − log ⁡ P ( Y = y i ∣ X = x i ) L_i = -\log P(Y = y_i|X = \mathbf{x}_i) Li=−logP(Y=yi∣X=xi)

现在我们回到前面的例子来计算一下。

1. 未归一化的对数概率：蓝色框里的数字是模型对每个类别的预测值，但尚未转换为概率。
2. 我们在获得预测值后，我们将进行指数转换：将每个分数通过指数函数转换为未归一化的概率：
   e 3.2 ≈ 24.5325 e^{3.2}≈24.5325 e3.2≈24.5325
   e 5.1 ≈ 164.021 e^{5.1}≈164.021 e5.1≈164.021
   e − 1.7 ≈ 0.182 e^{−1.7}≈0.182 e−1.7≈0.182
   我们进行保留小数点操作得到上面红色框里的数字。
3. 计算总和以计算归一化概率
   总和 = e 3.2 + e 5.1 + e − 1.7 ≈ 188.7355 总和=e^{3.2}+e^{5.1}+e^{−1.7}≈188.7355 总和=e3.2+e5.1+e−1.7≈188.7355
   因此,对于猫的概率: P ( cat ) = e 3.2 总和 ≈ 24.5325 188.7355 ≈ 0.130 P(\text{cat}) = \frac{e^{3.2}}{\text{总和}} \approx \frac{24.5325}{188.7355} \approx 0.130 P(cat)=总和e3.2≈188.735524.5325≈0.130
   对于汽车（car）的概率： P ( car ) = e 5.1 总和 ≈ 164.021 188.7355 ≈ 0.870 P(\text{car}) = \frac{e^{5.1}}{\text{总和}} \approx \frac{164.021}{188.7355} \approx 0.870 P(car)=总和e5.1≈188.7355164.021≈0.870
   对于青蛙（frog）的概率： P ( frog ) = e − 1.7 总和 ≈ 0.182 188.7355 ≈ 0.001 P(\text{frog}) = \frac{e^{-1.7}}{\text{总和}} \approx \frac{0.182}{188.7355} \approx 0.001 P(frog)=总和e−1.7≈188.73550.182≈0.001
   我们进行保留小数点操作得到上面绿色框里的数字。
4. 最后，如果我们已知图像的真实标签是猫（cat），那么我们可以使用损失函数计算损失：
   L i = − log ⁡ P ( Y = y i ∣ X = x i ) L_i = -\log P(Y = y_i|X = \mathbf{x}_i) Li=−logP(Y=yi∣X=xi)
   因此就是 L i = − log ⁡ P ( Y = y i ∣ X = x i ) L_i = -\log P(Y = y_i | X = \mathbf{x}_i) Li=−logP(Y=yi∣X=xi)
   ≈ − log ⁡ ( 0.130 ) \approx -\log(0.130) ≈−log(0.130)
   ≈ 2.040 \approx 2.040 ≈2.040

我们同样提出两个问题

1. Softmax分类器的损失函数 L i L_i Li可能的最小值和最大值是多少。
   最小值：0
   当模型完全正确时，损失达到最小值。即，模型将所有的概率（1.0）都分配给了真实类别： − log ⁡ ( P ( Y = y i ∣ X = x i ) ) = 0 -\log(P(Y = y_i | X = \mathbf{x}_i))=0 −log(P(Y=yi∣X=xi))=0
   最大值：无穷大
   当模型完全正确时，损失达到最小值。即，模型给真实类别的预测概率无限接近于 0： − log ⁡ ( P ( Y = y i ∣ X = x i ) ) = + ∞ -\log(P(Y = y_i | X = \mathbf{x}_i))=+∞ −log(P(Y=yi∣X=xi))=+∞
2. 通常在模型初始化时，权重矩阵 W W W的值都是较小的数字，因此在这种情况下，所有的分数 s s s都接近于0。那么，在这种情况下，损失函数 L i L_i Li的值是多少？
   我们继续像之前一样假设 s j ≈ 0 s_j≈0 sj≈0，根据前面步骤我们进行计算，我们将分数通过指数函数转换为未归一化的概率后便得到 e s j = 1 e^{s_j}=1 esj=1
   因此，对于任意类别 k k k（包括真实类别 y i y_i yi），其概率为： 1 C \frac{1} {C} C1
   代入损失公式那就是 L i ≈ − l o g ( 1 C ) = − ( l o g ( 1 ) − l o g ( C ) ) = − ( 0 − l o g ( C ) ) = l o g ( C ) L_i≈−log(\frac{1} {C})=−(log(1)−log(C))=−(0−log(C))=log(C) Li≈−log(C1)=−(log(1)−log(C))=−(0−log(C))=log(C)， C C C是类别数。

2.3 总结

我们学习了支持向量机（SVM）和Softmax分类器在处理多类分类问题时的损失计算方法。

下图展示了输入特征向量 x i x_i xi与权重矩阵 W W W相乘，然后加上偏置 b b b，得到每个类别的原始分数。

之后我们可以使用SVM的合页损失（Hinge Loss）或者Softmax的交叉熵损失（Cross-Entropy Loss）来计算损失。

这两种方法都旨在提高模型的分类性能，但它们在处理损失时的方法不同。SVM更关注于最大化类别间的间隔，而Softmax更关注于优化概率分布。

现在我们假设有三个分数向量：[10, -2, 3]、[10, 9, 9] 和 [10, -100, -100]，且 y i = 0 y_i=0 yi=0（即正确类别是第一个类别）。

问题是：如果我稍微改变一个数据点的分数，在这两种方法下损失会发生什么变化？

SVM 损失是分段常数或分段线性的，对得分的微小变化不敏感，除非变化跨越了"边界临界点"。

Softmax 损失是永远可微的，对得分的任何微小变化都高度敏感。

换句话来说，softmax分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小。但是，SVM只要边界值被满足了就满意了，不会超过限制去细微地操作具体分数。这可以被看做是SVM的一种特性。