01_机器学习初步

文章目录

[1 绪论](#1 绪论)
- [1.1 引言](#1.1 引言)
- [1.2 基本术语](#1.2 基本术语)
- - [1.2.1 数据基本概念](#1.2.1 数据基本概念)
  - [1.2.2 数据集与空间映射](#1.2.2 数据集与空间映射)
  - [1.2.3 模型相关](#1.2.3 模型相关)
  - [1.2.4 任务类型](#1.2.4 任务类型)
  - [1.2.5 监督范式](#1.2.5 监督范式)
  - [1.2.6 理论基础与泛化](#1.2.6 理论基础与泛化)
  - [1.2.7 学习理论](#1.2.7 学习理论)
[2 模型评估与选择](#2 模型评估与选择)
- [2.1 误差和过拟合](#2.1 误差和过拟合)
- [2.2 评估方法](#2.2 评估方法)
- - [2.2.1 留出法(Hold-out)](#2.2.1 留出法(Hold-out))
  - [2.2.2 交叉验证法(Cross Validation, CV)](#2.2.2 交叉验证法(Cross Validation, CV))
  - [2.2.3 自助法(Bootstrap)](#2.2.3 自助法(Bootstrap))
- [2.3 性能度量](#2.3 性能度量)
- - [2.3.1 回归任务(Regression)](#2.3.1 回归任务(Regression))
  - [2.3.2 分类任务(Classification)](#2.3.2 分类任务(Classification))
- [2.4 比较检验](#2.4 比较检验)
[3 线性模型](#3 线性模型)

1 绪论

1.1 引言

机器学习：利用经验改善系统自身的性能。

任何经验在计算机内都以数据形式存在。

计算问题分类：

P问题：可以在多项式时间（合理时间）内求解
NP问题：在多项式时间内求不出答案，但可以验证一个解

在计算学习理论当中，有一个很重要的理论模型PAC模型。

如果对于任意小的：

误差上限 ε > 0 ε>0 ε>0（表示学得多接近真理）
置信下限 1 − δ 1−δ 1−δ（表示学得多可靠）

存在一个多项式时间算法，能从有限样本中学到一个假设 h h h，满足：
P ( e r r o r ( h ) ≤ ε ) ≥ 1 − δ {P(error(h)≤ε)≥1−δ} P(error(h)≤ε)≥1−δ

也就是说：以至少 1 − δ 1−δ 1−δ 的概率，学到的模型错误率不超过 ε ε ε。

机器学习面对的很多问题，既不是P问题也不是NP问题，这些问题通常是可验证的优化问题，只能从数据中学到近似最优解（高概率正确）。

1.2 基本术语

1.2.1 数据基本概念

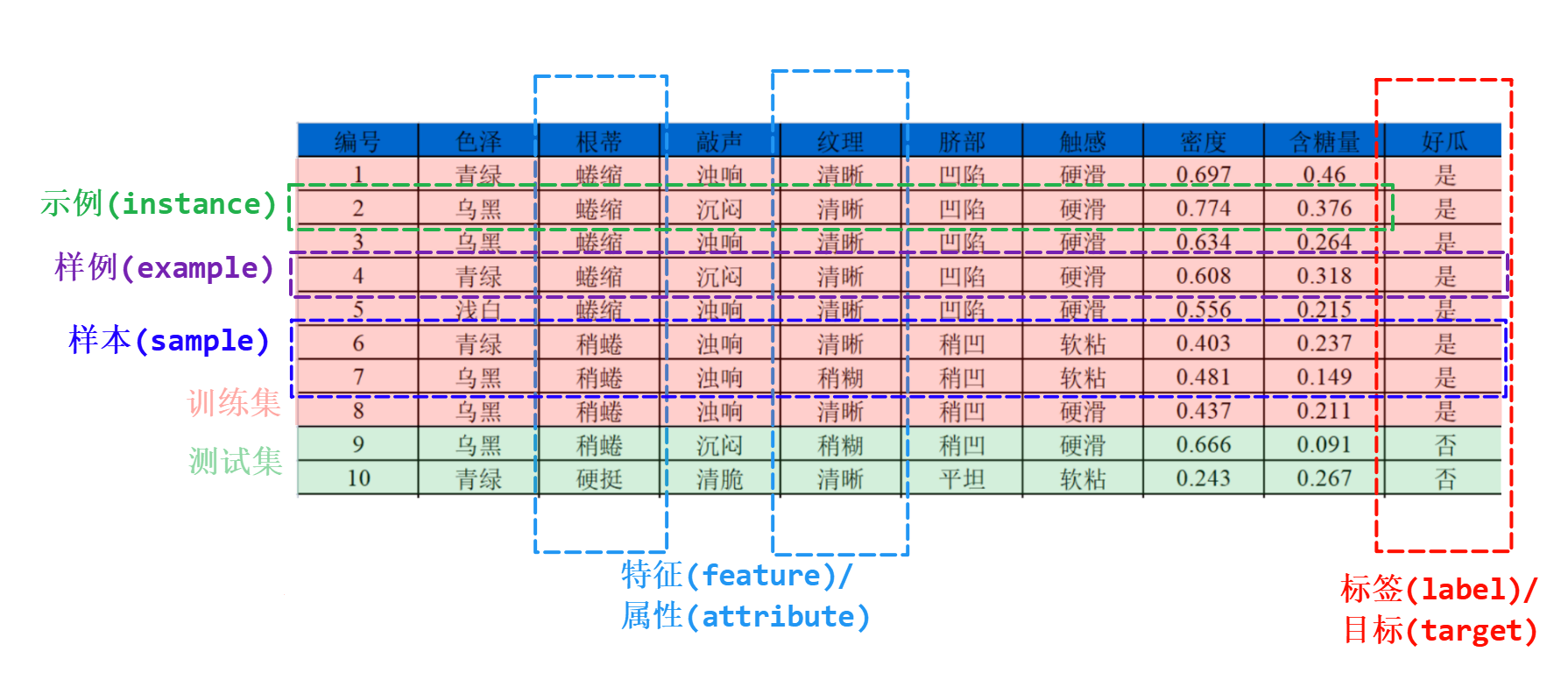
标签(label)/目标(target)：模型要预测的结果
特征(feature)/属性(attribute)：从数据中抽取出来的，对结果预测有用的信息
示例(instance)：一个具体的输入对象，即一行特征数据，不包含标签。
样例(example)：带有标签的一行数据
样本(sample)：一行或几行，或整个数据集都可以叫样本

1.2.2 数据集与空间映射

参数(parameter)：模型通过训练自动学习得到的数值，用于描述模型本身
超参数(hyperparameter)：训练开始前人为设定的参数，控制模型的学习过程或结构，不会在训练中自动学习
数据集：
- 训练集(training set)：用来训练模型的数据
- 验证集(validation set)：用于调参或选择模型
- 测试集(testing set)：用来测试模型的数据
机器学习的目标就是学习一个映射函数 f : X → Y f: \mathcal{X} \rightarrow \mathcal{Y} f:X→Y ，逼近真实映射函数 f ∗ : X → Y f^*: \mathcal{X} \rightarrow \mathcal{Y} f∗:X→Y
- 属性空间/特征空间/输入空间：输入特征的所有可能取值集合 X \mathcal{X} X
- 标签空间/目标空间/输出空间：输出结果的所有可能取值集合 Y \mathcal{Y} Y
特征向量(feture vector)：示例在属性空间中的一个点

1.2.3 模型相关

机器学习就是：学习器(learner)基于已标注数据(ground truth)，在假设空间中寻找最优假设(hypothesis)，使其在未知样本上尽可能逼近真实规律(true function)。

真相函数(true function)：世界的真实规律，不可知
真值(ground truth)：我们已知的、标注好的真实标签
学习器(learner)：训练算法，从数据中学习规律，寻找最优假设
假设(hypothesis)：学习器学出来的近似函数，用来逼近真值

1.2.4 任务类型

分类：根据输入特征，预测离散的类别标签
- 二分类：判断样本属于两种类别中的哪一种，如猫/狗
  - 正类：我们关注的目标类，通常用标签1表示，如患病
  - 反类：与正类相对的非目标类，通常用标签0表示，如健康
  - 正/反类是人为定义的，没有绝对好坏，根据视角不同，可以调换
- 多分类：判断样本属于多个类别中的哪一种，如猫/狗/鸟
回归：根据输入特征，预测一个连续数值，如预测房价

1.2.5 监督范式

监督学习(Supervised Learning) ：用带标签的数据来训练模型，学习输入与输出的映射，常用于分类和回归任务
无监督学习(Unsupervised Learning) ：数据没有标签，模型要自己发现规律或结构，常用于聚类和降维任务
半监督学习(Semi-supervised Learning)：只有少量样本带标签，通过少量监督信息引导整体学习
强化学习(Reinforcement Learning)：：模型通过与环境交互、不断试错，根据奖励信号优化策略，以获得最大奖励

1.2.6 理论基础与泛化

独立同分布(i.i.d.)：大多数机器学习理论的基本假设
1. 独立 (independent)：每个样本的生成不依赖其他样本
2. 同分布 (identically distributed)：所有样本都来自同一个概率分布
未见样本(unseen instance)：模型在训练时没有见过的样本
未知分布：训练集和测试集都是从这个分布抽样的，机器学习的目标就是学习到一个模型，使它对这个未知分布的整体表现尽可能好
泛化(generalization)：模型在未见样本上的表现能力

1.2.7 学习理论

归纳偏好：学习器在多种可能假设中倾向选择某一类假设的偏好，是学习的前提
无免费午餐定理(No Free Lunch, NFL)：对所有可能的数据分布而言，没有任何算法在所有任务上都优于其他算法，如果一个算法在某些任务上表现好，那它必然在其他任务上表现差

NFL定理的前提是所有问题出现的机会相同，或所有问题同样重要。脱离具体问题，空谈什么算法好没有意义。

2 模型评估与选择

奥卡姆剃刀原则主张在有多个同样有效的解释时，应选择最简单的那个解释。核心理念是"如无必要，勿增实体"。但判断什么样的模型算简单这个问题并不简单。

2.1 误差和过拟合

经验误差并不是越低越好，如果太低可能会导致过拟合，使泛化误差升高。

经验误差：在训练集上的误差
泛化误差：在未来样本上的误差

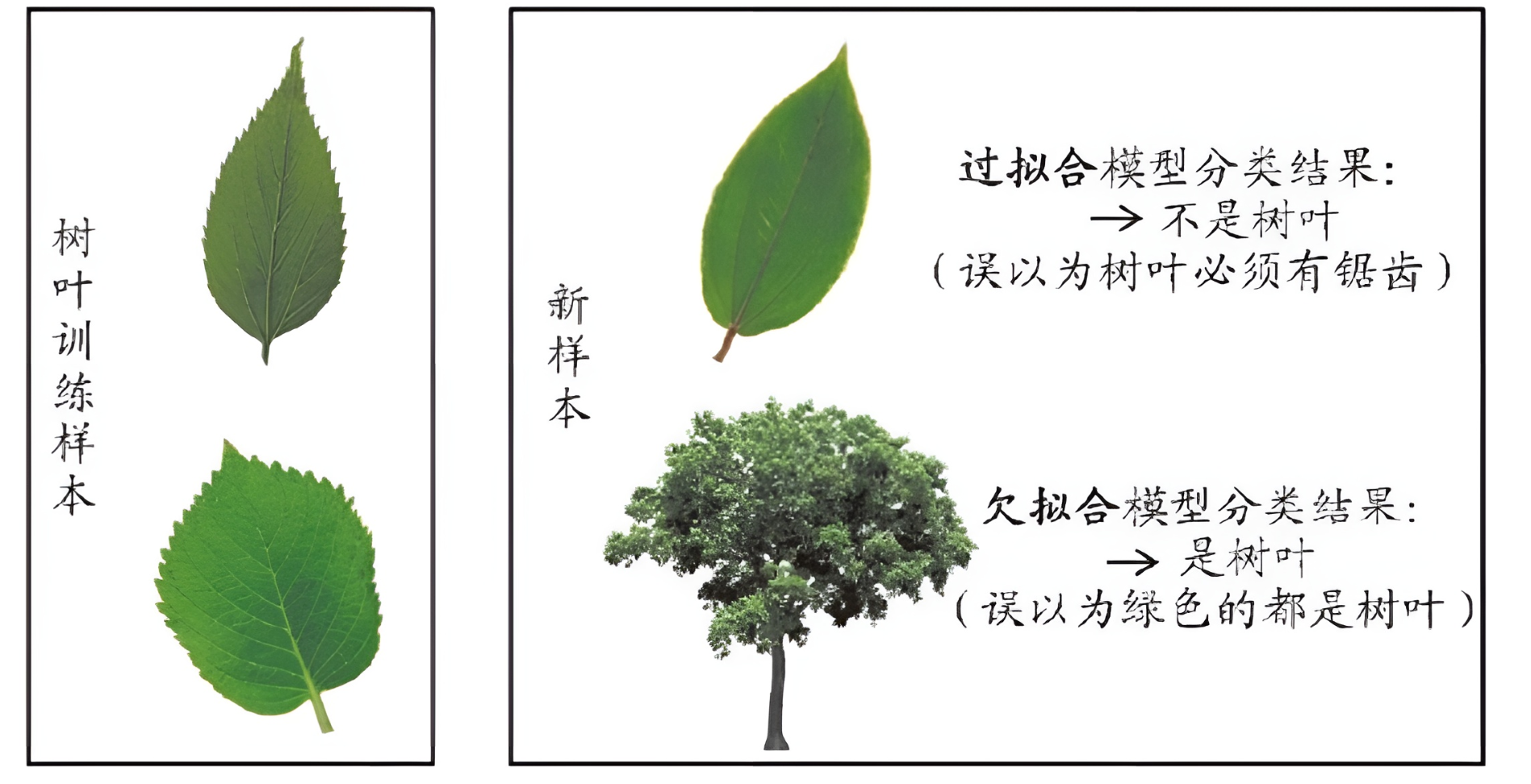
过拟合(overfitting) ：模型在训练集上学得太好，甚至记住了噪声或偶然特征，导致在训练集表现好、测试集表现差。
欠拟合(underfitting) ：模型对训练数据学习不足，连训练集都拟合不好，模型太简单、能力不够，无法捕捉数据中的真实规律。

如何获得测试结果？评估方法

如何评估性能优劣？性能度量

如何判断实质差别？比较检验

2.2 评估方法

模型训练流程：

初始划分：将原始数据划分为训练集 + 验证集 + 测试集。
模型训练阶段：在训练集 上训练模型，在验证集上调参、选择最优模型结构，训练过程中验证集不参与梯度更新，只是用来评估。
模型选择阶段：使用验证集表现最好的参数，重新用训练集 + 验证集合并训练一次，得到最终模型。
模型评估阶段：用测试集测试模型性能，测试集只用于一次性、最终评估，不能再回头调参。
模型部署阶段：最终确认算法后，可以用全量数据（训练+验证+测试）重新训练一个生产模型，使模型能利用所有可用数据进行学习。

2.2.1 留出法(Hold-out)

核心思想：将数据随机分成多个部分，一部分用于训练模型，另一部分用于验证和测试模型。它既可用于模型评估，也可用于模型选择。

优点：简单、计算量小，适合大数据集。
缺点：对数据划分方式敏感，数据量少时，训练集和测试集都可能不足。

注意：

保证数据分布一致性，例如使用分层采样
多次重复划分，例如100次随机划分
测试集要适中，太大影响模型训练效果，太小影响模型测试效果

常见比例：

训练集 : 测试集 = 7 : 3 或 8 : 2

三划分时：训练 6，验证 2，测试 2

模型评估：

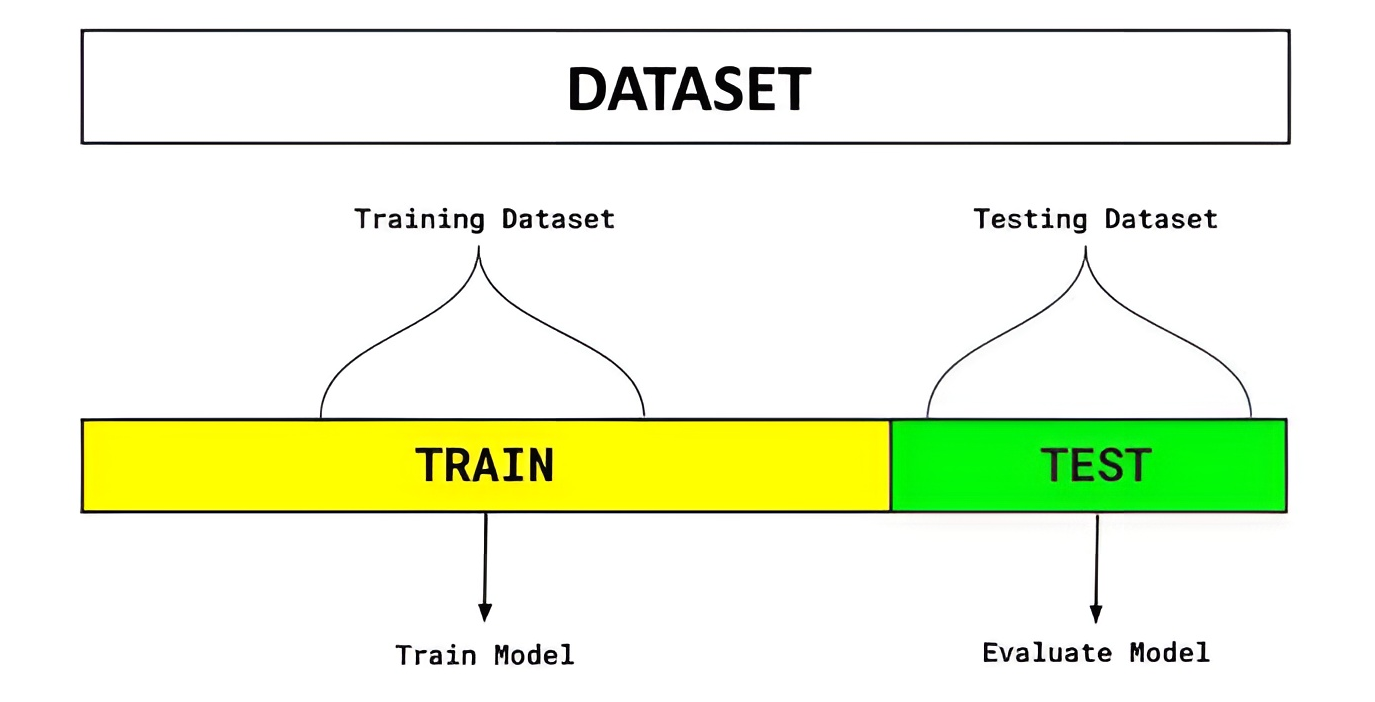
模型选择：

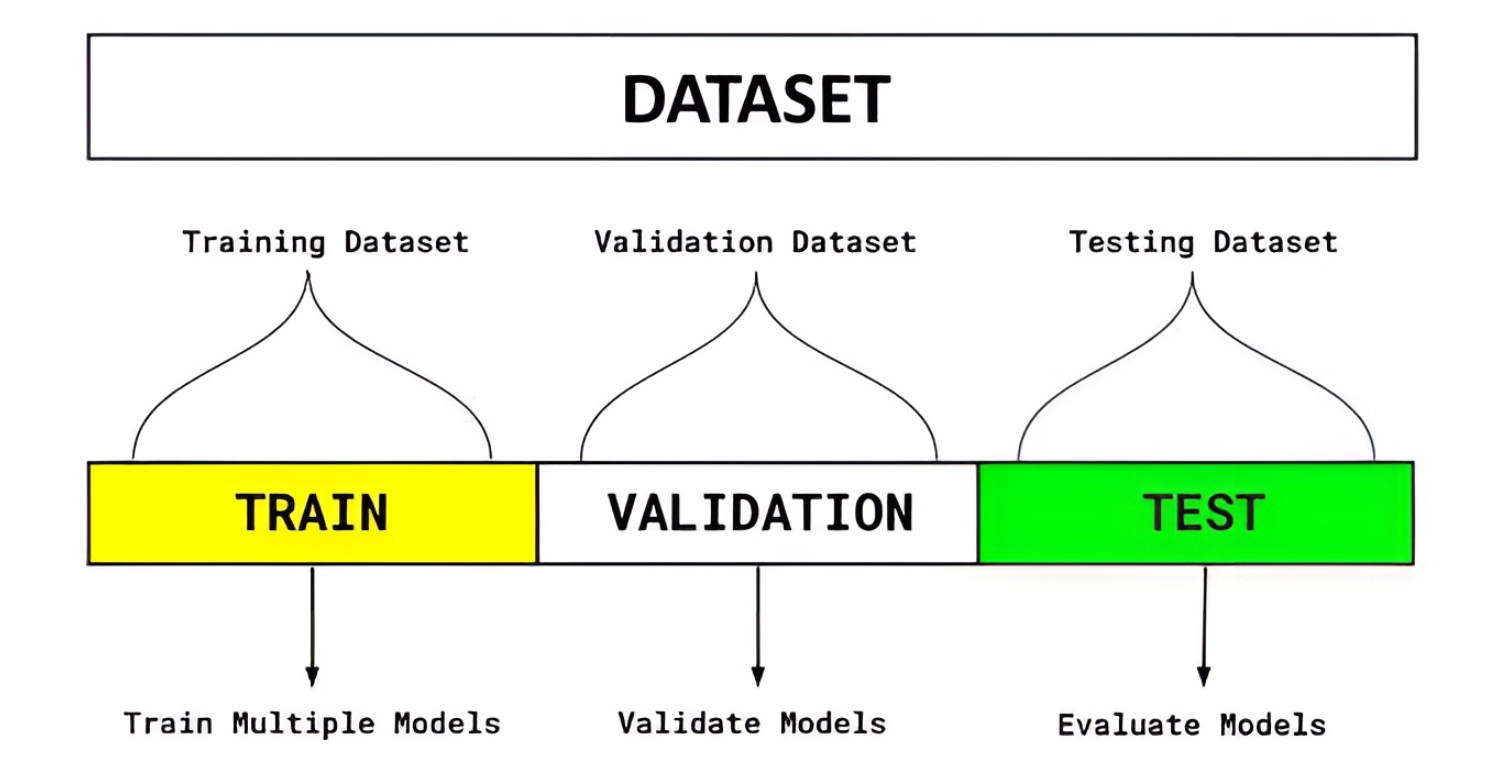
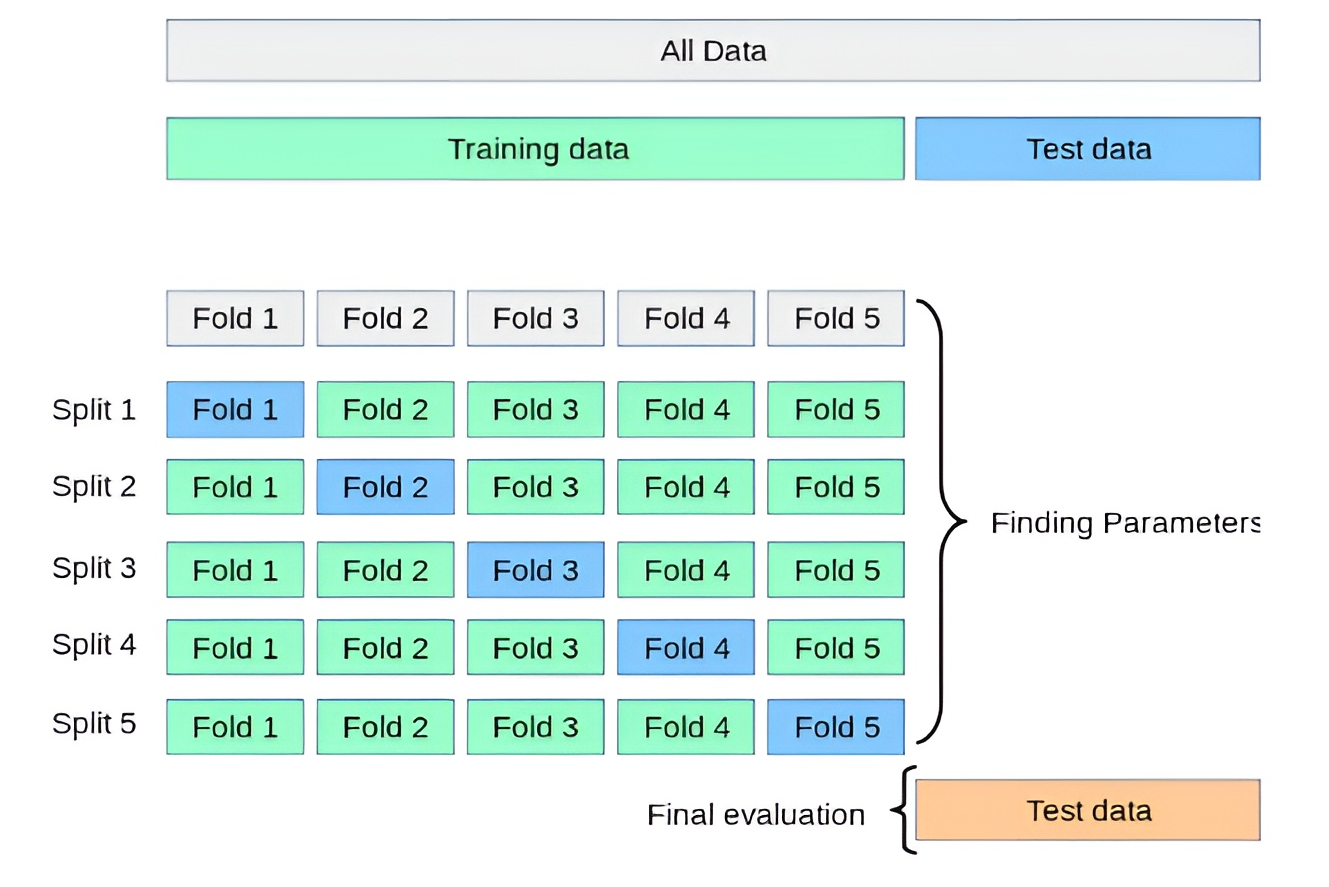
2.2.2 交叉验证法(Cross Validation, CV)

核心思想 ：将数据划分为 K 个折（fold），每次用 K−1 折训练、剩下 1 折测试，循环 K次，每个子集都做一次测试集，取平均度量作为性能估计。

常见形式：

K折交叉验证(K-Fold CV)：最常见，K一般取10，还有5、20等
留一法(Leave-One-Out, LOO)：K = 样本数，每次只留 1 个样本作验证

优点：每个样本都参与训练与验证，充分利用数据，评估结果稳定可靠
缺点：计算成本高

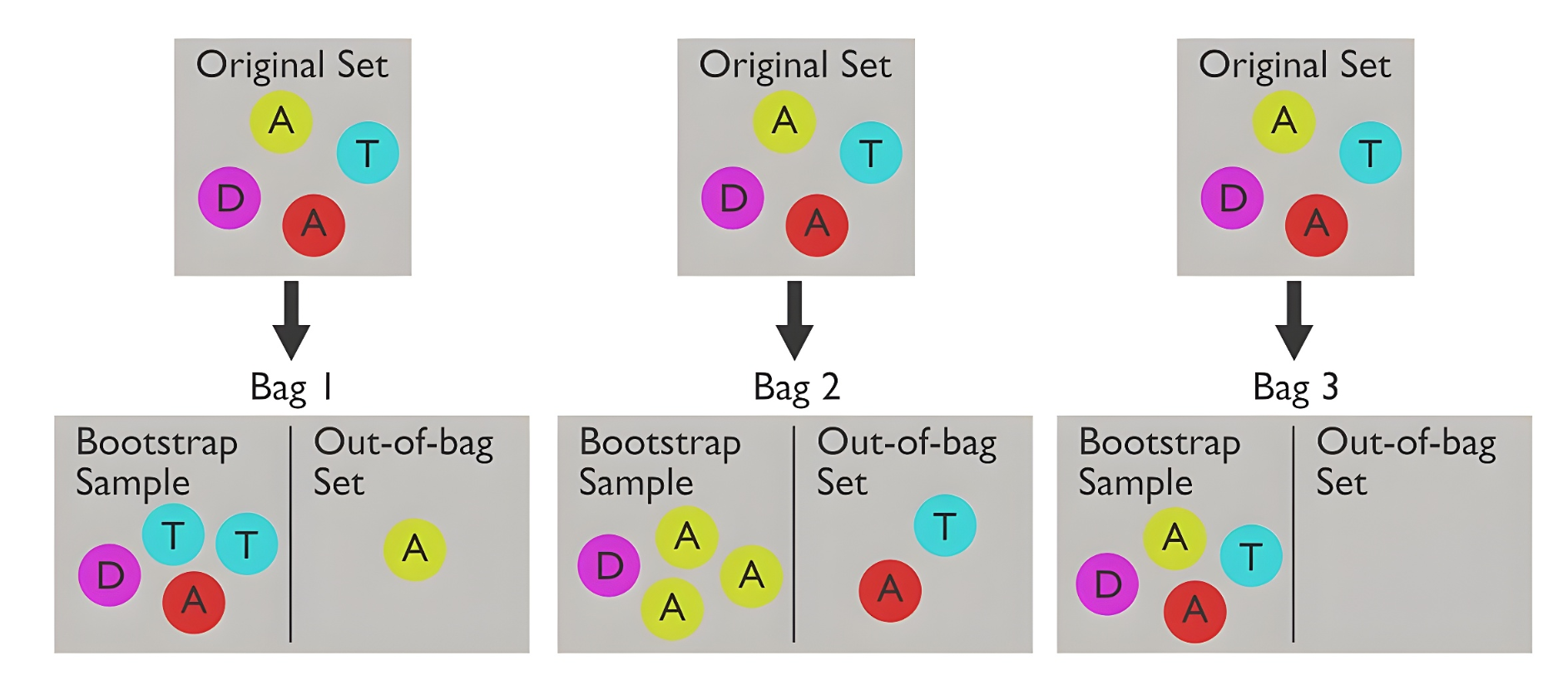
2.2.3 自助法(Bootstrap)

当数据集非常小，以至于划分训练/测试集都感觉很奢侈时，自助法就派上用场了。

核心思想 ：从原始数据集中进行有放回采样，形成与原数据等大小的训练集。从未被采样过的样本称为袋外(out-of-bag, OOB)测试集，每次自主采样约有 36.8% 成为 OOB。

优点：在数据集较小、难以有效划分训练/测试集时非常有用
缺点：有放回采样，改变了原始数据集的分布

2.3 性能度量

2.3.1 回归任务(Regression)

均方误差 (Mean Squared Error, MSE) ：每个样本的预测值与真实值之差的平方 的平均值。
M S E = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 {MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1i=1∑n(yi−y^i)2

平方会对较大的误差给予更高的惩罚，MSE的值越小，说明模型的预测越精准，性能越好。

RMSE（均方根误差） ： MSE \sqrt{\text{MSE}} MSE ，与原量纲一致。

2.3.2 分类任务(Classification)

混淆矩阵(Confusion Matrix) ：正类为 Positive §，负类为 Negative (N)。

总样本数 n = T P + T N + F P + F N n=TP+TN+FP+FN n=TP+TN+FP+FN。

真实类别	预测为正例	预测为反例
正例 §	TP (真正例)	FN (假反例)
反例 (N)	FP (假正例)	TN (真反例)

精度(Accuracy) ：预测正确的比例。
A c c u r a c y = T P + T N n Accuracy=\frac{TP+TN}{n} Accuracy=nTP+TN
错误率(Error) ：预测错误的比例。
E r r o r = F P + F N n = 1 − A c c u r a c y Error=\frac{FP+FN}{n}=1−Accuracy Error=nFP+FN=1−Accuracy
查准率(Precision) ：预测为正例的样本中，真正为正的比例，衡量模型预测的准不准。
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP

核心特点：宁缺毋滥。

查准率高，意味着模型在说一个样本是正例时，有很高的可信度。误报代价高时更关心，比如垃圾邮件检测。

查全率/召回率(Recall) ：真正的正例中，被模型判正的比例，衡量模型找得全不全。
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP

核心特点：宁多报不漏报。

查全率高，意味着模型能够把绝大多数的正例都找出来，很少漏掉。漏报代价高时更关心，比如病毒检测。

F1度量(F1-score) ：查准率和查全率是相互制约的，需要一个综合性的指标来平衡它们，F1度量就是它们的调和平均数，同时兼顾了查准率和查全率。
1 F 1 = 1 2 ⋅ ( 1 P r e c i s i o n + 1 R e c a l l ) \frac{1}{F_1}=\frac{1}{2}·(\frac{1}{Precision}+\frac{1}{Recall}) F11=21⋅(Precision1+Recall1)

得=>
F 1 = 2 ⋅ P r e c i s i o n + R e c a l l P r e c i s i o n ⋅ R e c a l l F_1=2⋅\frac{Precision+Recall}{Precision⋅Recall} F1=2⋅Precision⋅RecallPrecision+Recall
F-beta度量 ：不平衡场景可用加权的 F β F_β Fβ 强调召回或查准。
F β = ( 1 + β 2 ) ⋅ P R β 2 P + R F_β=(1+β^2)⋅\frac{PR}{β^2P+R} Fβ=(1+β2)⋅β2P+RPR

当 β > 1 β>1 β>1 时，更看重Recall（如 F 2 F_2 F2 度量）
当 β < 1 β<1 β<1 时，更看重Precision（如 F 0.5 F_{0.5} F0.5 度量）

2.4 比较检验

McNemar检验

于交叉验证t检验

3 线性模型

待更新。。。