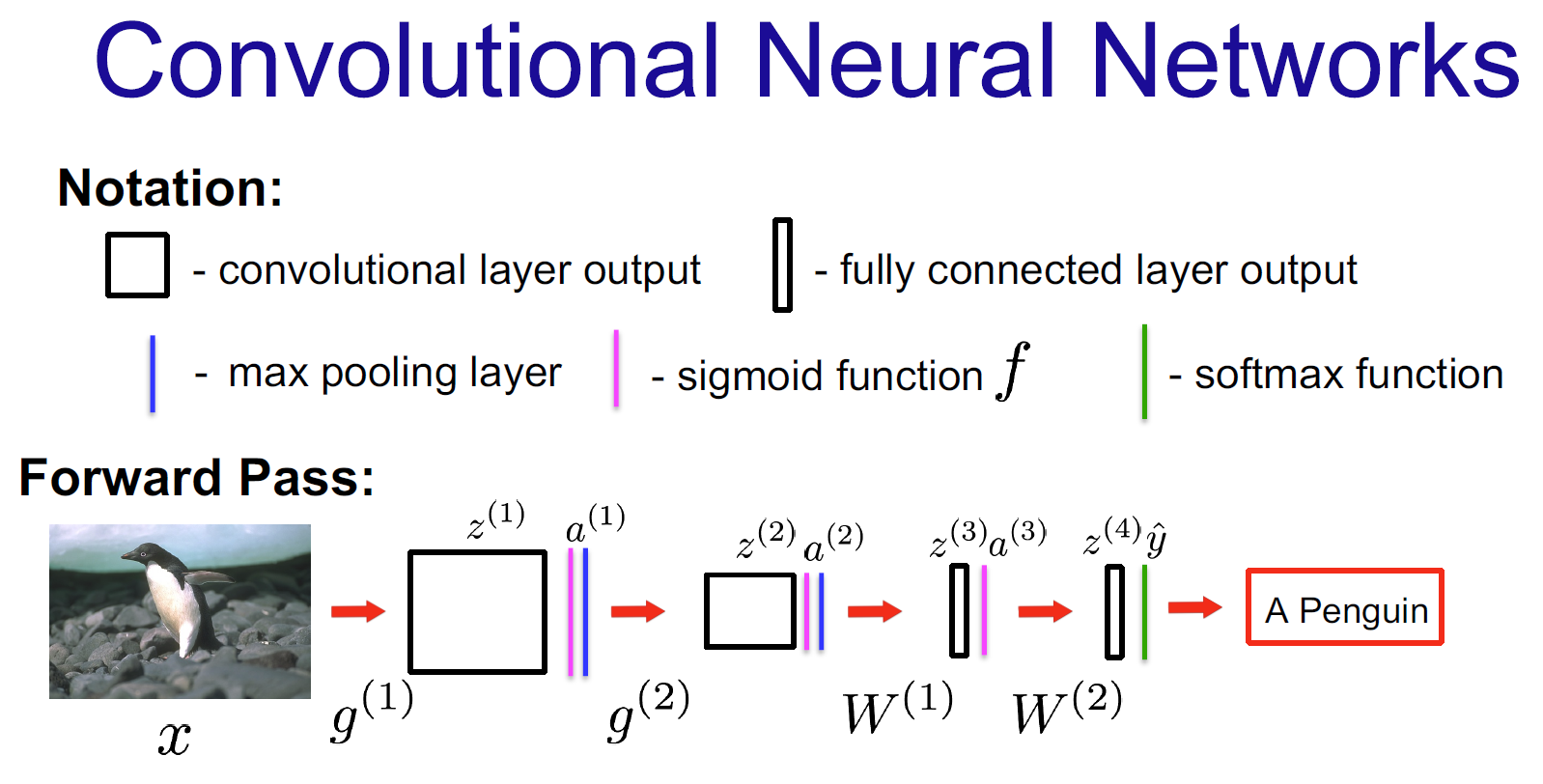
在这张图示的卷积神经网络中,通过反向传播需要学习的参数是以下四组:
-
第一层卷积核 : g ( 1 ) g^{(1)} g(1)
- 这是网络的第一层,用于从输入图像(企鹅)中提取初级特征。
-
第二层卷积核 : g ( 2 ) g^{(2)} g(2)
- 这是网络的第二层,用于从第一层的输出 a ( 1 ) a^{(1)} a(1) 中提取更高级的特征。
-
第一个全连接层权重 : W ( 1 ) W^{(1)} W(1)
- 在特征图经过展开后,第一个全连接层的权重矩阵。
-
第二个全连接层权重 : W ( 2 ) W^{(2)} W(2)
- 最后一个全连接层的权重矩阵,其输出 z ( 4 ) z^{(4)} z(4) 会传递给 softmax 函数以产生最终的预测 y ^ \hat{y} y^。
总结一下 :需要学习的参数是 g ( 1 ) g^{(1)} g(1), g ( 2 ) g^{(2)} g(2), W ( 1 ) W^{(1)} W(1), W ( 2 ) W^{(2)} W(2)。
这些参数的值在训练开始时是随机初始化的,然后通过反向传播算法,根据网络输出 y ^ \hat{y} y^ 与真实标签之间的误差,逐步进行调整和优化,以使网络的预测变得越来越准确。图中所示的 Max Pooling 层和 Sigmoid/Softmax 激活函数本身没有需要学习的参数,它们执行的是固定的运算。
那z和a需要改变吗?
简短的回答是: 是的,z 和 a 的值在训练期间肯定会改变,但它们本身不是通过梯度下降直接"学习"的参数,而是作为计算梯度所必需的中间变量。
下面我们来详细解释这其中的区别:
1. 需要"学习"的参数 vs. 前向传播的"结果"
-
参数 :指的是 g ( 1 ) g^{(1)} g(1), g ( 2 ) g^{(2)} g(2), W ( 1 ) W^{(1)} W(1), W ( 2 ) W^{(2)} W(2)。
- 这些是模型的本质。它们定义了网络如何从输入映射到输出。
- 它们在训练开始时被初始化,并在整个训练过程中被持续更新和保存。训练完成后,我们就是用这些学到的参数来对新数据进行预测。
- 它们是我们要通过梯度下降直接优化的目标。
-
z 和 a :指的是 z ( 1 ) , a ( 1 ) , z ( 2 ) , a ( 2 ) , z ( 3 ) , a ( 3 ) , z ( 4 ) z^{(1)}, a^{(1)}, z^{(2)}, a^{(2)}, z^{(3)}, a^{(3)}, z^{(4)} z(1),a(1),z(2),a(2),z(3),a(3),z(4)。
- 它们是特定输入 (比如这张企鹅图片)在当前参数 下,通过网络前向传播时产生的中间结果。
- 它们是动态的 :
- 对于不同的输入图片,它们的值不同。
- 随着参数 g , W g, W g,W 在训练中被更新,即使是同一张图片,再次前向传播时,产生的 z 和 a 也会不同。
- 训练完成后,我们不保存 某张特定图片的 z 和 a。我们只保存学到的参数 g , W g, W g,W。当有新图片需要预测时,我们将其输入网络,用学到的参数重新计算 z 和 a。
一个很好的类比:
想象一个函数 y = w x + b y = wx + b y=wx+b。
- 参数 : w w w 和 b b b。这是我们通过数据要学习的。
- 中间变量 :对于某个特定的输入 x x x,计算出的 y y y 就是结果。这个 y y y 依赖于 x , w , b x, w, b x,w,b。我们不会去"学习"这个 y y y,它只是计算过程中的一个值。
2. z 和 a 在反向传播中扮演的关键角色
虽然我们不直接"学习" z 和 a,但它们在反向传播中至关重要。它们的值被用来计算参数的梯度。
回顾链式法则,为了计算损失 L L L 对参数 W ( 2 ) W^{(2)} W(2) 的梯度,我们需要:
∂ L ∂ W ( 2 ) = ∂ L ∂ z ( 4 ) ⋅ ∂ z ( 4 ) ∂ W ( 2 ) \frac{\partial L}{\partial W^{(2)}} = \frac{\partial L}{\partial z^{(4)}} \cdot \frac{\partial z^{(4)}}{\partial W^{(2)}} ∂W(2)∂L=∂z(4)∂L⋅∂W(2)∂z(4)
而 z ( 4 ) = W ( 2 ) a ( 3 ) z^{(4)} = W^{(2)} a^{(3)} z(4)=W(2)a(3)(假设没有偏置项),所以 ∂ z ( 4 ) ∂ W ( 2 ) = a ( 3 ) \frac{\partial z^{(4)}}{\partial W^{(2)}} = a^{(3)} ∂W(2)∂z(4)=a(3)。
这意味着,为了知道 W ( 2 ) W^{(2)} W(2) 应该怎么更新,我们必须知道前一层的激活值 a ( 3 ) a^{(3)} a(3)。
同样地,在卷积层,计算 ∂ L ∂ g ( 1 ) \frac{\partial L}{\partial g^{(1)}} ∂g(1)∂L 时,公式中会用到输入 x x x 和上一层的误差信号。
所以,在反向传播过程中:
- 前向传播 :我们计算并保存 所有层的 z z z 和 a a a。这是因为在反向计算梯度时,我们需要用到它们在前向传播时的具体数值。
- 反向传播 :我们利用损失函数和保存的 z , a z, a z,a 值,从后往前依次计算每一层的梯度 ∂ L ∂ z \frac{\partial L}{\partial z} ∂z∂L 和 ∂ L ∂ a \frac{\partial L}{\partial a} ∂a∂L(误差信号),并最终计算出对参数 g , W g, W g,W 的梯度。
- 参数更新 :我们使用计算出的梯度来更新参数 g , W g, W g,W。
总结
- 学习/更新 :指的是通过梯度下降直接调整 g ( 1 ) g^{(1)} g(1), g ( 2 ) g^{(2)} g(2), W ( 1 ) W^{(1)} W(1), W ( 2 ) W^{(2)} W(2) 这些参数的值。
- 改变 : z z z 和 a a a 的值会间接改变 ,因为它们是参数和输入数据的函数。当参数被更新后,同样的输入再次通过网络时,会产生新的 z z z 和 a a a。它们是计算梯度所必需的中间变量,而不是学习的最终目标。
因此,在训练过程中,我们主动更新的是参数(Weights),而中间变量(z和a)的值是随之被动变化的,它们记录了数据在前向传播时的状态,是反向传播的"路标"。