【论文精读】ICLR 2023 --- 作为离线强化学习强表达能力策略类的扩散策略

文章目录

- abstract
- instruction
- [preliminaries and related work](#preliminaries and related work)
- [diffusion Q-Learning](#diffusion Q-Learning)
- [policy regularization](#policy regularization)
- experiments
- 代码框架

abstract

离线强化学习（Offline Reinforcement Learning, RL）旨在利用先前收集的静态数据集学习最优策略，是强化学习领域的重要范式。标准强化学习方法在该场景下往往表现不佳，原因在于对分布外动作（out-of-distribution actions）的函数逼近存在误差 。尽管已有多种正则化方法被提出以缓解这一问题，但这些方法通常受限于表达能力有限的策略类（policy classes with limited expressiveness），可能导致最终解的性能严重次优。

本文提出将策略表示为扩散模型 （diffusion model）------ 一类近年来涌现的、具有极强表达能力的深度生成模型。我们引入扩散 Q 学习 （Diffusion Q-learning, Diffusion-QL），利用条件扩散模型对策略进行建模。在该方法中，我们首先学习一个动作价值函数（action-value function），并在条件扩散模型的训练损失中加入一项最大化动作价值的目标项，最终得到的损失函数会引导模型生成接近行为策略（behavior policy）且最优的动作。

我们通过理论分析证明了基于扩散模型的策略具有极强的表达能 力，同时验证了扩散模型框架下行为克隆 （behavior cloning）与策略改进（policy improvement）的耦合机制是 Diffusion-QL 取得优异性能的核心原因。

在一个具有多模态行为策略的简单 2D 老虎机（bandit）示例中，我们直观展示了所提方法相较于现有工作的优越性；随后在 D4RL 基准测试的大部分任务中，我们进一步验证了该方法能够达到当前最优（state-of-the-art）的性能。

instruction

离线强化学习（Offline Reinforcement Learning, RL），又称批量强化学习（batch RL），旨在完全利用先前收集的数据学习有效的策略 ，无需与环境进行交互（Lange 等人，2012; Fujimoto 等人，2019）。由于省去了与环境在线交互的需求，离线强化学习在众多现实应用中具有极强的吸引力，例如自动驾驶和患者治疗规划 ------ 在这些场景中，使用未训练成熟的策略进行真实环境探索存在风险、成本高昂或耗时费力。

离线强化学习不依赖真实环境探索，而是强调利用先验数据（如人类示范数据），这类数据的获取成本通常远低于在线交互。

然而，仅依赖先前收集的数据也使得离线强化学习成为一项极具挑战性的任务。将标准的策略改进方法应用于离线数据集时，通常会涉及对数据集中未出现过的动作进行价值评估，而这些动作的价值往往难以准确估计。因此，朴素的离线强化学习方法通常会学到性能较差的策略：它们倾向于选择那些价值被高估的分布外动作，最终导致不理想的性能表现（Fujimoto 等人，2019）。

现有离线强化学习的研究工作主要通过以下四种方式解决这一问题：

正则化策略与行为策略的偏离程度；
约束所学价值函数，使其对分布外动作分配较低的价值；
引入基于模型的方法，通过学习环境动力学模型，在所学的马尔可夫决策过程（Markov Decision Process, MDP）中进行悲观规划；
将离线强化学习视为带回报引导的序列预测问题。

本文提出的方法属于第一类。

从实证结果来看，基于策略正则化的离线强化学习方法在性能上通常略逊于其他方法。我们的研究表明，这主要是因为现有策略正则化方法的性能受限 ------ 它们难以准确表示行为策略，进而导致正则化对策略改进产生不利影响。例如，策略正则化可能会将智能体的探索空间限制在一个仅包含次优动作的狭小区域，使得 Q 学习最终收敛到次优策略。

策略正则化不准确的问题主要源于两个原因：

策略类的表达能力不足
正则化方法设计不当

在大多数现有工作中，策略被建模为高斯分布 ，其均值和对角协方差由神经网络的输出指定。然而，离线数据集通常是由多个策略混合生成的，真实的行为策略可能呈现出强多模态性、偏态分布特性，或不同动作维度之间存在依赖关系 ------ 这些特性均无法通过对角高斯策略得到良好建模（Shafiullah 等人，2022）。

一个极端但并不罕见的例子是：使用高斯策略通过最小化数据分布与策略分布之间的 KL 散度（Kullback--Leibler divergence）来拟合双模态训练数据。这会导致策略出现 "模态覆盖" 行为，即在两个模态的中间区域分配高概率密度，而该区域实际上是训练数据的低密度区域。在这种情况下，将新策略向行为克隆得到的策略进行正则化，反而会显著恶化策略学习效果。

其次，诸如 KL 散度和最大均值差异（Maximum Mean Discrepancy, MMD）等正则化方法（Kumar 等人，2019）通常并不适合离线强化学习场景：KL 散度需要获取明确的概率密度值，而 MMD 则需要在每个状态下采样多个动作以进行优化。这些方法都需要额外步骤：先学习一个行为克隆策略，为 KL 优化提供密度值，或为 MMD 优化提供随机动作样本。而由于策略类的表达能力限制，行为克隆得到的策略可能无法很好地建模真实行为策略，因此将当前策略向该克隆策略进行正则化会进一步引入逼近误差。我们在第 4 节设计了一个简单的老虎机（bandit）实验，结果表明即使在这类简单任务中，上述问题也可能出现。

在本文中，我们提出一种基于扩散模型（或分数匹配模型）的策略正则化方法 （Sohl-Dickstein 等人，2015; Song & Ermon, 2019; Ho 等人，2020）。具体而言，我们采用基于多层感知机（Multilayer Perceptron, MLP）的去噪扩散概率模型（Denoising Diffusion Probabilistic Model, DDPM）（Ho 等人，2020）作为策略。我们为扩散模型设计的损失函数包含两项：

行为克隆项，用于引导扩散模型采样出与训练集分布一致的动作；
策略改进项，用于引导模型采样出高价值动作（基于所学的 Q 值函数）。

我们的扩散模型是一个条件模型，以状态为输入条件，以动作作为输出。将扩散模型应用于此场景具有多个显著优势：

首先，扩散模型具有极强的表达能力，能够很好地捕捉多模态分布；
其次，扩散模型的损失函数本身就是一种强大的分布匹配技术 ，因此可被视为一种高效的基于样本的策略正则化方法，无需额外的行为克隆步骤；
最后，扩散模型通过迭代优化过程生成动作，Q 值最大化的引导信号可以在每个逆扩散步骤中加入。

综上所述，本文的核心贡献是提出了扩散 Q 学习（Diffusion-QL）------ 一种新的离线强化学习算法。该算法利用扩散模型实现精准的策略正则化 ，并成功将 Q 学习的引导信号注入逆扩散过程中，以寻找最优动作。

离散强化学习

强化学习中的环境通常由马尔可夫决策过程（Markov Decision Process, MDP）定义：
M = { S , A , P , R , γ , d 0 } \mathcal{M} = \{ \mathcal{S}, \mathcal{A}, P, R, \gamma, d_0 \} M={S,A,P,R,γ,d0}，其中 S \mathcal{S} S为状态空间， A \mathcal{A} A为动作空间，环境动力学 P ( s ′ ∣ s , a ) : S × S × A → [ 0 , 1 ] P(s' \mid s, a): \mathcal{S} \times \mathcal{S} \times \mathcal{A} \to [0, 1] P(s′∣s,a):S×S×A→[0,1]描述状态转移概率，奖励函数 R : S × A → R R: \mathcal{S} \times \mathcal{A} \to \mathbb{R} R:S×A→R输出即时奖励，折扣因子 γ ∈ [ 0 , 1 ) \gamma \in [0, 1) γ∈[0,1)权衡当前与未来奖励的重要性， d 0 d_0 d0为初始状态分布 （Sutton & Barto, 2018）。强化学习的目标是学习一个由参数 θ \theta θ表征的策略 π θ ( a ∣ s ) \pi_\theta(a \mid s) πθ(a∣s)，最大化累积折扣奖励的期望 E [ ∑ t = 0 ∞ γ t r ( s t , a t ) ] \mathbb{E}\left[ \sum_{t=0}^\infty \gamma^t r(s_t, a_t) \right] E[∑t=0∞γtr(st,at)]。策略 π \pi π的动作价值函数 （或称 Q 值函数）定义为： Q π ( s t , a t ) = E a t + 1 , a t + 2 , ⋯ ∼ π [ ∑ t = 0 ∞ γ t r ( s t , a t ) ] Q^\pi(s_t, a_t) = \mathbb{E}{a{t+1}, a_{t+2}, \dots \sim \pi}\left[ \sum_{t=0}^\infty \gamma^t r(s_t, a_t) \right] Qπ(st,at)=Eat+1,at+2,⋯∼π[t=0∑∞γtr(st,at)]，即从状态 s t s_t st执行动作 a t a_t at后遵循策略 π \pi π所能获得的期望累积奖励。

在离线场景中（Fu 等人，2020），算法不直接与环境交互，而是利用由行为策略 π b \pi_b πb收集的静态数据集 D ≜ { ( s , a , r , s ′ ) } \mathcal{D} \triangleq \{ (s, a, r, s') \} D≜{(s,a,r,s′)}进行学习。离线强化学习算法完全基于该静态离线数据集 D \mathcal{D} D训练策略，无需在线环境交互。

扩散模型

基于扩散的生成模型，假设数据分布 p θ ( x 0 ) : = ∫ p θ ( x 0 : T ) d x 1 : T p_\theta(x_0) := \int p_\theta(x_{0:T}) dx_{1:T} pθ(x0):=∫pθ(x0:T)dx1:T，其中 x 1 , ... , x T x_1, \dots, x_T x1,...,xT是与数据 x 0 ∼ p ( x 0 ) x_0 \sim p(x_0) x0∼p(x0)维度相同的潜在变量。前向扩散过程通过T步逐步向数据 x 0 ∼ q ( x 0 ) x_0 \sim q(x_0) x0∼q(x0)添加噪声（噪声方差由预定义的方差调度 β i \beta_i βi控制），其概率分布可表示为： q ( x 1 : T ∣ x 0 ) : = ∏ t = 1 T q ( x t ∣ x t − 1 ) q(x_{1:T} \mid x_0) := \prod_{t=1}^T q(x_t \mid x_{t-1}) q(x1:T∣x0):=t=1∏Tq(xt∣xt−1)，其中 q ( x t ∣ x t − 1 ) : = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t \mid x_{t-1}) := \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) q(xt∣xt−1):=N(xt;1−βt xt−1,βtI)

( N (\mathcal{N} (N表示高斯分布，I为单位矩阵）。反向扩散过程构建为 p θ ( x 0 : T ) : = N ( x T ; 0 , I ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) p_\theta(x_{0:T}) := \mathcal{N}(x_T; 0, I) \prod_{t=1}^T p_\theta(x_{t-1} \mid x_t) pθ(x0:T):=N(xT;0,I)t=1∏Tpθ(xt−1∣xt)，通过最大化证据下界（Evidence Lower Bound, ELBO） E q [ ln ⁡ p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] \mathbb{E}q\left[ \ln \frac{p\theta(x_{0:T})}{q(x_{1:T} \mid x_0)} \right] Eq[lnq(x1:T∣x0)pθ(x0:T)]进行优化（Jordan 等人，1999; Blei 等人，2017）。训练完成后，扩散模型的采样过程 为：先从 p ( x T ) p(x_T) p(xT)采样初始噪声 x T x_T xT，再通过反向扩散链从 t = T t=T t=T迭代到 t = 0 t=0 t=0，最终生成数据 x 0 x_0 x0。通过将反向扩散分布扩展为 p θ ( x t − 1 ∣ x t , c ) p_\theta(x_{t-1} \mid x_t, c) pθ(xt−1∣xt,c)（c为条件变量），可直接得到条件扩散模型。

对比维度	Diffuser（轨迹级生成）	Diffusion-QL（动作级生成）
扩散模型的生成对象	完整轨迹（一串 ( s t , a t ) (s_t,a_t) (st,at)）	单个动作（当前s对应的a）
模型框架	基于模型（依赖轨迹规划，隐含环境动力学假设）	无模型（不建模环境，依赖 Q 函数评估价值）
引导信号的注入时机	推理阶段（反向采样时注入回报模型信号）	训练阶段（损失函数中直接加入 Q 值引导项）
推理时的计算成本	高（生成完整轨迹，仅用第一个动作）	低（仅生成单个动作，直接执行）
核心依赖组件	轨迹生成器 + 独立回报模型	条件动作生成器 + Q 值函数（无模型组件）
通俗类比	出门前先规划好全程路线（哪怕中途会变），再出发	出门前只确定下一步走哪里（看当前路况 + 目的地方向），走一步看一步

diffusion Q-Learning

本节首先说明如何将条件扩散模型用作具有强表达能力的行为克隆策略 ，随后介绍如何在训练阶段将 Q 学习引导信号融入扩散模型的学习过程，其中行为克隆项同时起到策略正则化的作用。

扩散策略

符号定义 ：由于本文涉及两种不同类型的时间步（扩散过程时间步与强化学习轨迹时间步），我们采用上标 i ∈ { 1 , ... , N } i \in \{1, \dots, N\} i∈{1,...,N}表示扩散时间步 ，下标 t ∈ { 1 , ... , T } t \in \{1, \dots, T\} t∈{1,...,T}表示轨迹时间步。

我们通过条件扩散模型的逆过程来表示强化学习策略：
π θ ( a ∣ s ) = p θ ( a 0 : N ∣ s ) = N ( a N ; 0 , I ) ∏ i = 1 N p θ ( a i − 1 ∣ a i , s ) \pi_\theta(a \mid s) = p_\theta(a_{0:N} \mid s) = \mathcal{N}(a_N; 0, I) \prod_{i=1}^N p_\theta(a_{i-1} \mid a_i, s) πθ(a∣s)=pθ(a0:N∣s)=N(aN;0,I)i=1∏Npθ(ai−1∣ai,s)其中，逆扩散链的最终样本 a 0 a_0 a0即为用于强化学习评估的动作。

扩散模型生成动作的过程是"从纯噪声开始，经过N次迭代（扩散时间步 i ），最终得到动作 a 0 a_0 a0 "。--------- 每次迭代 i（从 N = 10 N=10 N=10到 i = 1 i=1 i=1），用 a i a_i ai生成更接近 "有效动作" 的 a i − 1 a_{i-1} ai−1（比如(i=10)是纯噪声，(i=9)是 "模糊的向左走"，...，(i=1)是 "清晰的向前走"）；最终的 a 0 a_0 a0就是 AI 要执行的动作（"向前走"）。

通常，条件转移概率 p θ ( a i − 1 ∣ a i , s ) p_\theta(a_{i-1} \mid a_i, s) pθ(ai−1∣ai,s)可建模为高斯分布 N ( a i − 1 ; μ θ ( a i , s , i ) , Σ θ ( a i , s , i ) ) \mathcal{N}(a_{i-1}; \mu_\theta(a_i, s, i), \Sigma_\theta(a_i, s, i)) N(ai−1;μθ(ai,s,i),Σθ(ai,s,i))。

每次迭代生成 a i − 1 a_{i-1} ai−1时，遵循 "高斯分布" 规则，其中均值 μ θ \mu_\theta μθ由 "当前噪声 a i a_i ai" 和 "预测噪声 ϵ θ \epsilon_\theta ϵθ " 共同决定 ( ϵ θ (\epsilon_\theta (ϵθ是神经网络，负责预测 "需要去掉的噪声"）。

假设 i = 5 i=5 i=5，当前 a 5 a_5 a5是 "半噪声半动作" 的向量； ϵ θ ( a 5 , s , i = 5 ) \epsilon_\theta(a_5,s,i=5) ϵθ(a5,s,i=5)会预测 " a 5 a_5 a5里包含的噪声是多少"；代入公式后， μ θ \mu_\theta μθ会输出 "去掉噪声后的更清晰动作向量"；最终 a 4 a_4 a4会围绕 μ θ \mu_\theta μθ做小幅随机波动（由 β i I \beta_i I βiI控制波动范围）。

遵循 Ho 等人（2020）的设计，我们将 p θ ( a i − 1 ∣ a i , s ) p_\theta(a_{i-1} \mid a_i, s) pθ(ai−1∣ai,s)参数化为噪声预测模型：协方差矩阵固定为 Σ θ ( a i , s , i ) = β i I \Sigma_\theta(a_i, s, i) = \beta_i I Σθ(ai,s,i)=βiI（I为单位矩阵），均值 μ θ ( a i , s , i ) \mu_\theta(a_i, s, i) μθ(ai,s,i)构造为： μ θ ( a i , s , i ) = 1 α i ( a i − β i 1 − α ˉ i ϵ θ ( a i , s , i ) ) \mu_\theta(a_i, s, i) = \frac{1}{\sqrt{\alpha_i}} \left( a_i - \frac{\beta_i}{\sqrt{1 - \bar{\alpha}i}} \epsilon\theta(a_i, s, i) \right) μθ(ai,s,i)=αi 1(ai−1−αˉi βiϵθ(ai,s,i))

其中 α i = 1 − β i \alpha_i = 1 - \beta_i αi=1−βi， α ˉ i = ∏ k = 1 i α k \bar{\alpha}i = \prod{k=1}^i \alpha_k αˉi=∏k=1iαk（累积乘积）， ϵ θ \epsilon_\theta ϵθ为预测噪声的神经网络。扩散策略的采样过程如下：首先从标准高斯分布采样初始噪声 a N ∼ N ( 0 , I ) a_N \sim \mathcal{N}(0, I) aN∼N(0,I)，然后通过参数 θ \theta θ控制的逆扩散链迭代生成 a i − 1 a_{i-1} ai−1（i从N到1）：

a i − 1 ∣ a i = a i / α i − β i α i ( 1 − α ˉ i ) ϵ θ ( a i , s , i ) + β i ϵ , ϵ ∼ N ( 0 , I ) ( 1 ) a_{i-1} \mid a_i = a_i / \sqrt{\alpha_i} - \frac{\beta_i}{\sqrt{\alpha_i (1 - \bar{\alpha}i)}} \epsilon\theta(a_i, s, i) + \sqrt{\beta_i} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)(1) ai−1∣ai=ai/αi −αi(1−αˉi) βiϵθ(ai,s,i)+βi ϵ,ϵ∼N(0,I)(1)

遵循 DDPM（Ho 等人，2020）的设计，当 i = 1 i=1 i=1时，将 ϵ \epsilon ϵ设为0以提升采样质量。我们采用 Ho 等人（2020）提出的简化目标函数训练条件噪声模型 ϵ θ \epsilon_\theta ϵθ，损失函数定义为： L d ( θ ) = E i ∼ U , ϵ ∼ N ( 0 , I ) , ( s , a ) ∼ D [ ∥ ϵ − ϵ θ ( α ˉ i a + 1 − α ˉ i ϵ , s , i ) ∥ 2 ] ( 2 ) \mathcal{L}d(\theta) = \mathbb{E}{i \sim U, \epsilon \sim \mathcal{N}(0,I), (s,a) \sim \mathcal{D}} \left[ \left\| \epsilon - \epsilon_\theta\left( \sqrt{\bar{\alpha}_i} a + \sqrt{1 - \bar{\alpha}_i} \epsilon, s, i \right) \right\|^2 \right](2) Ld(θ)=Ei∼U,ϵ∼N(0,I),(s,a)∼D[ ϵ−ϵθ(αˉi a+1−αˉi ϵ,s,i) 2](2)

训练 ϵ θ \epsilon_\theta ϵθ（预测噪声的网络），让它能 "准确预测扩散过程中添加的噪声 "------ 这本质是 "模仿数据集里的动作分布"（行为克隆）。

从数据集 D \mathcal{D} D中取一个样本：状态s（"角色在目标点前 5 米"）、动作a（"向前走"）；随机选一个扩散时间步 i = 3 i=3 i=3，给a添加噪声（得到 α ˉ 3 a + 1 − α ˉ 3 ϵ \sqrt{\bar{\alpha}_3}a + \sqrt{1-\bar{\alpha}3}\epsilon αˉ3 a+1−αˉ3 ϵ，即 "带噪声的向前走"）；让 ϵ θ \epsilon\theta ϵθ预测 "这个噪声是多少"，并和真实添加的 ϵ \epsilon ϵ对比 ------ 预测越准， L d \mathcal{L}d Ld越小；训练完成后， ϵ θ \epsilon\theta ϵθ就能 "去掉噪声、还原出数据集里的动作分布"，让扩散模型生成的动作和专家动作（数据集）一致。

其中：

U表示离散集合 { 1 , ... , N } \{1, \dots, N\} {1,...,N}上的均匀分布（随机采样扩散时间步i）；
D \mathcal{D} D表示由行为策略 π b \pi_b πb收集的离线数据集；
输入 α ˉ i a + 1 − α ˉ i ϵ \sqrt{\bar{\alpha}_i} a + \sqrt{1 - \bar{\alpha}_i} \epsilon αˉi a+1−αˉi ϵ为前向扩散过程中 t = i t=i t=i时刻的带噪动作（模拟扩散过程的中间状态）。

该扩散模型损失 L d ( θ ) \mathcal{L}_d(\theta) Ld(θ)本质是行为克隆损失，其目标是学习行为策略 π b ( a ∣ s ) \pi_b(a \mid s) πb(a∣s)（即让模型采样出与训练数据分布一致的动作 ）。值得注意的是，逆扩散链的边缘分布提供了一种隐式且具有强表达能力的分布建模方式 ，能够捕捉离线数据集可能存在的复杂分布特性（如偏态分布、多模态分布等）。

逆扩散链的 "边缘分布"（即最终生成的动作分布）是隐式建模的，不需要预先定义分布形式 （比如不用假设动作是高斯分布），因此能捕捉数据集的复杂分布（比如 "同一状态下有多个最优动作" 的多模态分布、"动作偏向某一范围" 的偏态分布）。

此外，该正则化方法基于样本实现，仅需从数据集 D \mathcal{D} D和当前策略中随机采样（无需显式知晓行为策略 ------ 这在数据集来自人类示范等场景中尤为重要，因为真实行为策略往往不可知）。与现有方法常用的 "先行为克隆再正则化" 两步策略不同，我们的方法为灵活策略提供了一种简洁高效的正则化方式。

这里的 L d ( θ ) \mathcal{L}_d(\theta) Ld(θ)本身既是行为克隆（模仿数据），也是正则化（约束动作分布不偏离数据），是 "一步完成" 的简洁方案。

扩散模型的逆过程最终生成的动作 a 0 a_0 a0，其分布完全由训练数据决定：因为 ϵ θ \epsilon_\theta ϵθ是在 "数据集动作 + 噪声" 上训练的，只有当生成的动作贴近数据集分布时， ϵ θ \epsilon_\theta ϵθ才能准确预测噪声 ， L d ( θ ) \mathcal{L}_d(\theta) Ld(θ)才能最小化。------------------- 它不需要额外的约束项（比如传统方法的 KL 散度、MMD），而是通过 "模仿数据的训练过程 " 天然实现了 "约束动作分布不偏离数据"。

L d ( θ ) \mathcal{L}d(\theta) Ld(θ)的优化效率较高（每个数据点仅需采样一个扩散时间步i），但式（1）的逆扩散采样过程需要迭代调用N次 ϵ θ \epsilon\theta ϵθ网络，可能成为运行时间的瓶颈。因此，我们倾向于将N设为相对较小的值。为适配小N的场景（取 β min = 0.1 \beta_{\text{min}} = 0.1 βmin=0.1， β max = 10.0 \beta_{\text{max}} = 10.0 βmax=10.0），我们遵循 Xiao 等人（2021）的设计，采用以下方差调度： β i = 1 − α i = 1 − exp ⁡ ( − β min ⋅ 1 N − 0.5 ( β max − β min ) ⋅ 2 i − 1 N 2 ) \beta_i = 1 - \alpha_i = 1 - \exp\left( -\beta_{\text{min}} \cdot \frac{1}{N} - 0.5(\beta_{\text{max}} - \beta_{\text{min}}) \cdot \frac{2i-1}{N^2} \right) βi=1−αi=1−exp(−βmin⋅N1−0.5(βmax−βmin)⋅N22i−1)

该调度基于 Song 等人（2021）提出的方差保持随机微分方程（variance preserving SDE）推导得到，可在小N下保证扩散过程的稳定性。

在N很小的情况下，让 β i \beta_i βi的变化满足 "前向过程能逐步将数据转化为纯噪声、逆过程能从噪声稳定还原数据" 的规律。具体来说：

当i较小时（扩散初期）， β i \beta_i βi较小（添加的噪声少），保证数据的核心信息被保留；

当i接近N时（扩散后期），KaTeX parse error: Expected group after '_' at position 6: \beta_̲增大（添加的噪声多），保证最终能得到接近纯噪声的 a N a_N aN；

整个序列的 β i \beta_i βi变化是 "平滑且符合随机微分方程规律" 的，避免小N下扩散过程出现 "噪声添加不均匀、数据无法还原" 的问题。

Q-learning

策略正则化损失 L d ( θ ) \mathcal{L}_d(\theta) Ld(θ)仅实现行为克隆 ，无法让学到的策略性能超越生成训练数据的行为策略。为实现策略改进，我们在训练阶段将 Q 值函数引导信号注入逆扩散链，使模型优先采样高价值动作。最终的策略学习目标是策略正则化与策略改进的线性组合：

π = arg ⁡ min ⁡ π θ L ( θ ) = L d ( θ ) + L q ( θ ) = L d ( θ ) − α ⋅ E s ∼ D , a 0 ∼ π θ [ Q ϕ ( s , a 0 ) ] ( 3 ) \pi = \arg\min_{\pi_\theta} \mathcal{L}(\theta) = \mathcal{L}d(\theta) + \mathcal{L}q(\theta) = \mathcal{L}d(\theta) - \alpha \cdot \mathbb{E}{s \sim \mathcal{D}, a_0 \sim \pi\theta} \left[ Q\phi(s, a_0) \right](3) π=argπθminL(θ)=Ld(θ)+Lq(θ)=Ld(θ)−α⋅Es∼D,a0∼πθ[Qϕ(s,a0)](3)

其中：

L q ( θ ) \mathcal{L}_q(\theta) Lq(θ)为策略改进项（负号表示 "最大化 Q 值" 转化为最小化损失）；
a 0 a_0 a0通过式（1）的逆扩散过程重参数化生成，因此 Q 值函数关于动作的梯度可通过整个扩散链反向传播（保证策略参数 θ \theta θ能通过 Q 值引导更新）。

行为克隆 ( L d ( θ ) (\mathcal{L}_d(\theta) (Ld(θ)）只能让模型 "复刻专家的动作"，但无法学到比专家更好的策略。因此需要加入Q 值引导：让模型优先选择 "Q 值高" 的动作。

L d ( θ ) \mathcal{L}_d(\theta) Ld(θ)：行为克隆项（让模型模仿专家动作，比如 "怪物血量 50% 时用普通攻击"）；

L q ( θ ) = − α ⋅ E [ Q ϕ ( s , a 0 ) ] \mathcal{L}q(\theta) = -\alpha \cdot \mathbb{E}[Q\phi(s,a_0)] Lq(θ)=−α⋅E[Qϕ(s,a0)]：策略改进项（负号表示 "最大化 Q 值" 转化为 "最小化损失"）------ 让模型优先选 Q 值高的动作（比如 "技能攻击" Q 值更高，模型会倾向于选它）；

a 0 a_0 a0：扩散模型生成的动作 （比如 "普通攻击" 或 "技能攻击"），通过逆扩散过程生成，且梯度可反向传播（Q 值的高低能引导扩散模型调整生成动作的倾向）。

由于不同离线数据集的 Q 值函数尺度存在差异 ，为标准化 Q 值，我们遵循 Fujimoto & Gu（2021）的设计，将 α \alpha α设为： α = η E ( s , a ) ∼ D [ ∣ Q ϕ ( s , a ) ∣ ] \alpha = \frac{\eta}{\mathbb{E}{(s,a) \sim \mathcal{D}} \left[ |Q\phi(s,a)| \right]} α=E(s,a)∼D[∣Qϕ(s,a)∣]η其中 η \eta η为超参数（用于平衡两项损失的权重），分母中的Q仅用于标准化，不参与梯度计算。

Q 值函数本身采用传统方法训练：结合双重 Q 学习（double Q-learning）技巧（Hasselt, 2010），最小化贝尔曼算子误差（Lillicrap 等人，2015; Fujimoto 等人，2019）。具体来说，我们构建两个 Q 网络 Q ϕ 1 , Q ϕ 2 Q_{\phi_1}, Q_{\phi_2} Qϕ1,Qϕ2和对应的目标网络 Q ϕ 1 ′ , Q ϕ 2 ′ Q_{\phi'1}, Q{\phi'2} Qϕ1′,Qϕ2′，以及目标策略 π θ ′ \pi{\theta'} πθ′。通过最小化以下目标函数优化 Q 网络参数 ϕ i \phi_i ϕi（ i = 1 , 2 i=1,2 i=1,2）：

E ( s t , a t , s t + 1 ) ∼ D , a t + 1 ′ ∼ π θ ′ [ ( r ( s t , a t ) + γ min ⁡ i = 1 , 2 Q ϕ i ′ ( s t + 1 , a t + 1 ′ ) − Q ϕ i ( s t , a t ) ) 2 ] ( 4 ) \mathbb{E}{(s_t,a_t,s{t+1}) \sim \mathcal{D}, a'{t+1} \sim \pi{\theta'}} \left[ \left( r(s_t, a_t) + \gamma \min_{i=1,2} Q_{\phi'i}(s{t+1}, a'{t+1}) - Q{\phi_i}(s_t, a_t) \right)^2 \right](4) E(st,at,st+1)∼D,at+1′∼πθ′[(r(st,at)+γi=1,2minQϕi′(st+1,at+1′)−Qϕi(st,at))2](4)

让 "当前 Q 网络的预测值" 尽可能贴近 "真实的长期收益（目标值）"，通过最小化两者的平方差来优化 Q 网络。

Q 值函数 Q ϕ ( s , a ) Q_\phi(s,a) Qϕ(s,a)的作用是：评估 "在状态s下执行动作a，未来能获得的总收益"。训练的目标是让 Q 网络的预测值尽可能贴近 "真实的长期收益"。

当前 Q 网络： Q ϕ 1 Q_{\phi_1} Qϕ1、 Q ϕ 2 Q_{\phi_2} Qϕ2（共 2 个，参数分别为 ϕ 1 \phi_1 ϕ1、 ϕ 2 \phi_2 ϕ2）------ 用于实时预测 Q 值，是训练的对象；

目标 Q 网络： Q ϕ 1 ′ Q_{\phi'1} Qϕ1′、 Q ϕ 2 ′ Q{\phi'_2} Qϕ2′（共 2 个，参数分别为 ϕ 1 ′ \phi'_1 ϕ1′、 ϕ 2 ′ \phi'_2 ϕ2′）------ 用于计算 "真实长期收益的目标值"，参数采用软更新（比如 ϕ 1 ′ = 0.01 ϕ 1 + 0.99 ϕ 1 ′ \phi'_1 = 0.01\phi_1 + 0.99\phi'_1 ϕ1′=0.01ϕ1+0.99ϕ1′），避免训练震荡；

目标策略： π θ ′ \pi_{\theta'} πθ′------ 用于采样 "下一个状态的动作"，同样采用软更新。

其中：

r ( s t , a t ) r(s_t, a_t) r(st,at)为状态 s t s_t st执行动作 a t a_t at的即时奖励；
γ \gamma γ为折扣因子；
a t + 1 ′ ∼ π θ ′ a'{t+1} \sim \pi{\theta'} at+1′∼πθ′表示从目标策略采样的下一时刻动作；
目标网络和目标策略的参数采用软更新方式更新（避免训练震荡）。

我们在第 4 节和第 5 节进行了大量实验，结果表明 L d \mathcal{L}_d Ld（正则化 / 行为克隆）与 L q \mathcal{L}_q Lq（策略改进）的协同作用能实现最优性能。算法 1 总结了 Diffusion-QL 的完整实现流程。

policy regularization

本节通过一个2 维连续动作空间的简单老虎机任务，对比现有策略正则化方法与我们提出的条件扩散方法的工作机制。首先简要回顾现有方法。

现有方法回顾

1. BC-MLE

策略 π θ ( a ∣ s ) \pi_\theta(a \mid s) πθ(a∣s)被建模为高斯分布 N ( a ; μ θ ( s t ) , Σ θ ( s ) ) \mathcal{N}(a; \mu_\theta(s_t), \Sigma_\theta(s)) N(a;μθ(st),Σθ(s))，其中 μ θ \mu_\theta μθ和 Σ θ \Sigma_\theta Σθ通常由多层感知机（MLP）参数化（为简化， Σ θ \Sigma_\theta Σθ常设为对角矩阵）。策略通过最大化 E ( s , a ) ∼ D [ log ⁡ π θ ( a ∣ s ) ] \mathbb{E}{(s,a)\sim\mathcal{D}}[\log \pi\theta(a \mid s)] E(s,a)∼D[logπθ(a∣s)]优化。

TD3+BC（Fujimoto & Gu, 2021）：直接在策略学习中添加行为克隆（BC）损失作为额外项；
IQL（Kostrikov 等人，2021b）：利用 "样本内" 学习的优势函数，对期望中的对数项进行加权。

2. BC-CVAE

策略 π θ ( a ∣ s ) \pi_\theta(a \mid s) πθ(a∣s)由条件变分自编码器（CVAE）建模，包含编码器网络 q θ ( z ∣ s , a ) q_\theta(z \mid s,a) qθ(z∣s,a)和解码器网络 p θ ( a ∣ s , z ) p_\theta(a \mid s,z) pθ(a∣s,z)。通过最大化证据下界 E ( s , a ) ∼ D [ E z ∼ q ( ⋅ ∣ s , a ) [ log ⁡ p ( a ∣ s , z ) ] − KL ( q ( z ∣ s , a ) ∥ p ( z ) ) ] \mathbb{E}{(s,a)\sim\mathcal{D}}[\mathbb{E}{z\sim q(\cdot \mid s,a)}[\log p(a \mid s,z)] - \text{KL}(q(z \mid s,a)\|p(z))] E(s,a)∼D[Ez∼q(⋅∣s,a)[logp(a∣s,z)]−KL(q(z∣s,a)∥p(z))]优化（ p ( z ) p(z) p(z)通常设为标准高斯先验）。

BCQ（Fujimoto 等人，2019）：训练 CVAE 模型近似行为策略，再训练一个偏差模型，引导 CVAE 生成的动作向 Q 值较高的区域调整。

3. BC-MMD

BEAR（Kumar 等人，2019）同样通过 CVAE 模仿行为策略，并通过最小化最大均值差异（MMD）限制当前策略 π θ ( a ∣ s ) \pi_\theta(a \mid s) πθ(a∣s)与克隆的行为策略接近。策略采用 Tanh - 高斯形式（输出层添加 Tanh 激活的高斯网络）。

现有方法（如 BCQ、BEAR）的正则化是两步式：先学习行为策略的近似（行为克隆），再将策略改进得到的策略向克隆的行为策略正则化。但这种两步法的问题在于：第二步的策略正则化效果严重依赖 "克隆质量"，若克隆不准确，会误导后续的策略改进步骤。我们将在 2 维连续动作空间的老虎机示例中展示这一缺陷。

示例：2 维连续动作空间老虎机任务

我们考虑一个动作空间为 a ∈ [ − 1 , 1 ] 2 \boldsymbol{a} \in [-1, 1]^2 a∈[−1,1]2的简单老虎机任务，构建含 M = 10000 M=10000 M=10000个动作样本的离线数据集 D = { ( a j ) } j = 1 M \mathcal{D} = \{(a_j)\}_{j=1}^M D={(aj)}j=1M：动作由4 个高斯分布等权混合生成，中心为 μ ∈ { ( 0.0 , 0.8 ) , ( 0.8 , 0.0 ) , ( 0.0 , − 0.8 ) , ( − 0.8 , 0.0 ) } \mu \in \{(0.0, 0.8), (0.8, 0.0), (0.0, -0.8), (-0.8, 0.0)\} μ∈{(0.0,0.8),(0.8,0.0),(0.0,−0.8),(−0.8,0.0)}，标准差 σ d = ( 0.05 , 0.05 ) \sigma_d=(0.05, 0.05) σd=(0.05,0.05)（如图 1 第一幅图所示）。

该示例的行为策略分布具有强多模态性------ 这是数据集由多个策略（如不同人类操作者）收集时的常见情况（例如专家与业余操作者的动作分布属于不同模态）。

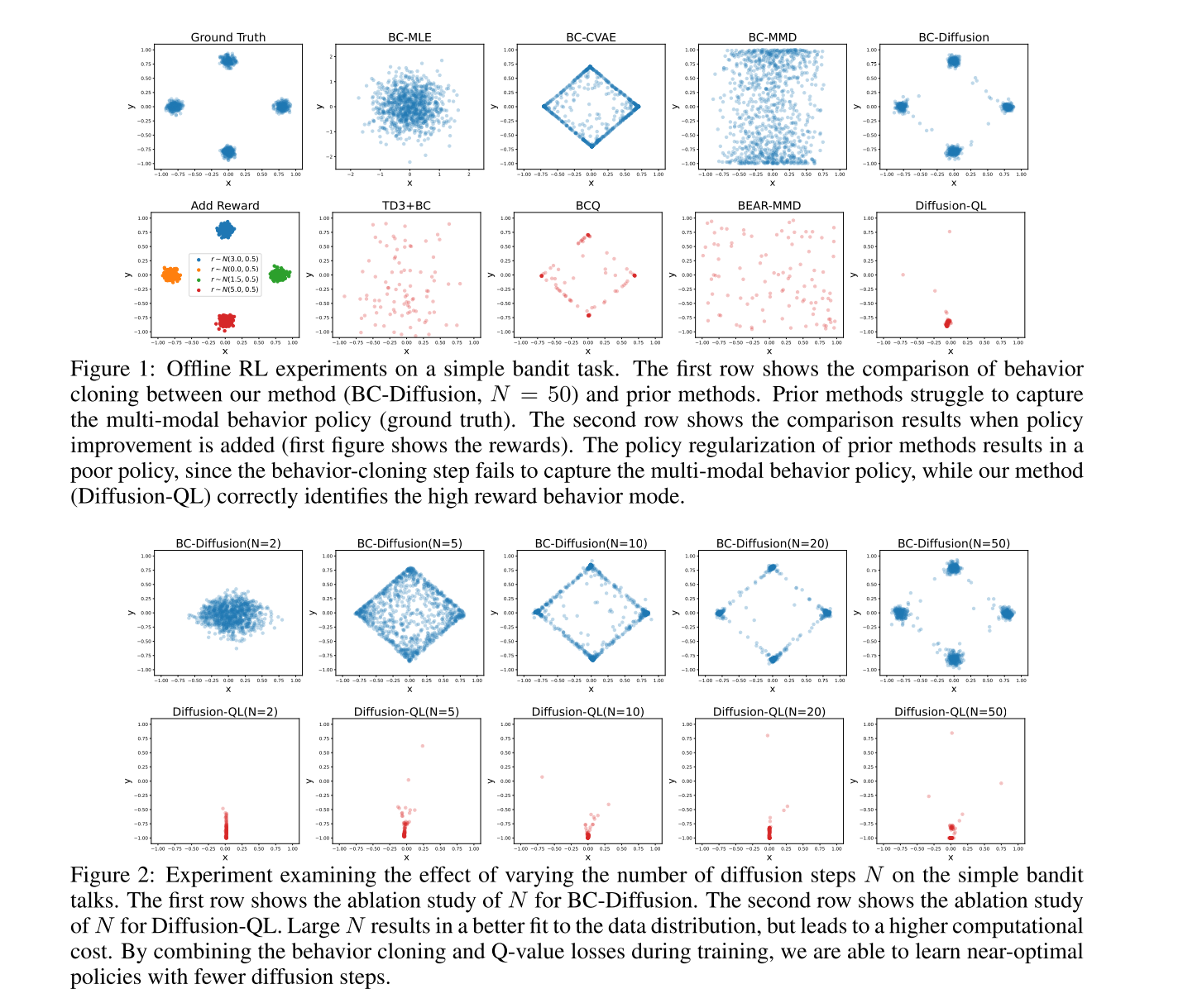
步骤 1：行为克隆任务的对比

首先在 "仅克隆行为策略（不做策略改进）" 的任务中，对比现有方法与扩散方法的表现（图 1 第一行）：

扩散模型：准确捕捉到行为策略的 4 个密度模态；
BC-MLE：受限于单高斯分布 的表达能力，呈现 "模态覆盖" 行为 ------ 用一个大标准差的高斯分布拟合 4 个模态，其高密度区域实际是真实行为策略的低密度区域；
CVAE 模型：虽为隐式模型，但仍出现模态覆盖 ------ 捕捉到 4 个模态，但在模态之间分配了高密度；且不同随机种子下，CVAE 有时无法覆盖所有 4 个模态；
BEAR 的 Tanh - 高斯策略：因表达能力有限，仅在边界线附近对齐密度，无法还原真实分布。

这一简单示例中现有方法的克隆失败，体现了它们在多模态行为策略场景下的局限性。

步骤 2：策略改进的影响

为每个数据点分配奖励（奖励服从高斯分布，均值由数据中心决定，标准差固定为 0.5，如图 1 第二行所示），模拟 "奖励函数未知、需学习" 的离线 RL 场景。对比 Diffusion-QL 与 TD3+BC、BCQ、BEAR-MMD 的表现（训练 1000 轮确保收敛）：

现有方法：因行为克隆正则化的约束，策略改进被限制在次优甚至错误的探索区域：
----TD3+BC：无法收敛到最优模态（行为策略的高密度区域是无离线数据的区域）；
---- BCQ：动作集中在 CVAE 克隆得到的 4 个对角角落；
---- BEAR-MMD：因正则化不准确，动作分布随机；
Diffusion-QL：成功收敛到最优的底部角落。原因是：
---- 扩散策略的强表达能力能还原行为策略，覆盖所有模态以支持后续探索；
---- 式 (3) 中线性组合的损失函数，让 Q 学习引导扩散策略在有效区域内寻找最优动作。

步骤 3：扩散时间步N的影响

进一步研究扩散时间步N对性能的影响（图 2）：

行为克隆任务 （图 2 第一行）：N越大，扩散模型的表达能力越强，能学到数据分布的更多细节；当 N = 50 N=50 N=50时，可准确还原真实数据分布；
策略改进任务 （图 2 第二行）：因式 (3) 的损失耦合，中等偏小的N即可达到良好性能。但N越大，扩散模型的克隆正则化约束越强：例如 N = 2 N=2 N=2时，仍有少量动作采样自无训练数据的区域； N = 50 N=50 N=50时，策略被约束在正确的数据区域内探索。

N是 Diffusion-QL 中 "策略表达能力" 与 "计算成本" 的权衡。在 D4RL 数据集上， N = 5 N=5 N=5即可取得良好表现，且足够小以实现高效训练与部署。

experiments

在主流的 D4RL 基准测试集 （Fu 等人，2020）上评估所提方法，并通过实证研究分析扩散模型的时间步数量影响，同时开展消融实验以验证 Diffusion-QL 两大核心组件的贡献。

数据集

我们选取 D4RL 基准中的四类任务域：Gym、AntMaze、Adroit 和 Kitchen，各任务域特性如下：

Gym-MuJoCo 移动任务：最常用的标准评估任务，难度相对较低 ------ 数据集包含大量近优轨迹，且奖励函数平滑；
AntMaze 任务 ：挑战性更高，采用稀疏奖励机制，需智能体拼接多条次优轨迹以寻找迷宫目标路径（Fu 等人，2020）；
Adroit 数据集：主要由人类行为数据构成，离线数据反映的状态 - 动作区域通常较狭窄，需强策略正则化确保智能体停留在有效区域；
Kitchen 环境：要求智能体按序完成 4 个目标子任务以达成期望状态配置，因此长期价值优化至关重要。

基线方法

我们选取各任务域中表现优异的不同类型基线方法，具体包括：

策略正则化类：经典行为克隆（BC）、BEAR（Kumar 等人，2019）、BRAC（Wu 等人，2019）、BCQ（Fujimoto 等人，2019）、TD3+BC（Fujimoto & Gu, 2021）、AWR（Peng 等人，2019）、AWAC（Nair 等人，2020）、IQL（Kostrikov 等人，2021b），以及基于单步改进的 Onestep RL（Brandfonbrener 等人，2021）；
Q 值约束类：REM（Agarwal 等人，2020）、CQL（Kumar 等人，2020）；
基于模型的离线强化学习类：MoRel（Kidambi 等人，2020）；
序列建模类：决策 Transformer（DT, Chen 等人，2021）、Diffuser（Janner 等人，2022）。

基线方法的性能结果均引用其原论文、Fu 等人（2020）或 Kostrikov 等人（2021b）报告的最优结果。

实验细节

训练设置：训练 1000 轮（Gym 任务为 2000 轮），每轮包含 1000 个梯度步，批次大小为 256；
训练稳定性 ：如图 3 所示，多数任务训练稳定，但 AntMaze 任务因稀疏奖励设置及数据集中缺乏最优轨迹，训练存在波动。为此，训练过程中保存多个模型检查点，采用附录 D 所述的纯离线方法选择最优检查点用于性能评估 ------ 以 L d \mathcal{L}_d Ld损失作为在线性能的滞后指标，执行早停策略，选择 L d \mathcal{L}_d Ld值第二或第三小的检查点。本文主要结果均基于该离线模型选择策略；若允许少量在线交互用于模型选择，性能可进一步提升（附录表 4）；
超参数N的影响 ：实证研究表明（图 3），随着扩散时间步N增大，模型收敛速度加快，性能更稳定 。在后续 D4RL 任务中，设置中等值 N = 5 N=5 N=5以平衡性能与计算成本 ------ 此时训练时间与 CQL（Kumar 等人，2020）相当；其他超参数：学习率、 η \eta η等其余超参数详见附录 E。

与其他方法的对比

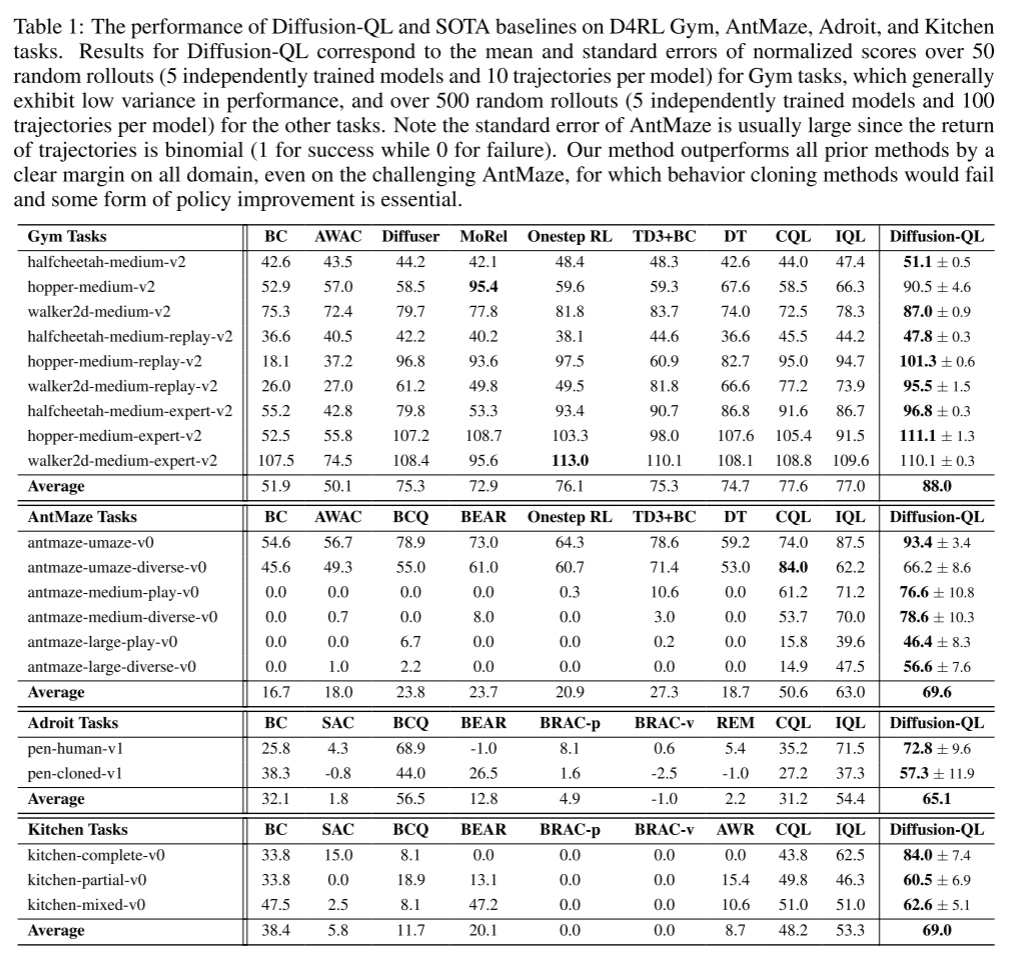
我们在四类任务域中将 Diffusion-QL 与基线方法进行对比，结果如表 1 所示，按任务域分析如下：

Gym 任务域结果

多数基线方法在 Gym 任务上已表现良好，但 Diffusion-QL 仍能显著提升性能，尤其在 "medium" 和 "medium-replay" 子任务中。需注意，"medium" 数据集的轨迹由在线 SAC 智能体（Haarnoja 等人，2018）收集，该智能体性能仅为专家的 1/3，其 Tanh - 高斯策略具有探索性且分布分散，导致数据分布难以学习。如第 4 节所示，扩散模型即便在复杂场景下仍具备模仿行为策略的强表达能力，随后策略改进项会引导策略在已探索的动作空间子集内收敛到最优动作 ------ 这两大组件是 Diffusion-QL 取得优异实证性能的关键。

AntMaze 任务域结果

稀疏奖励与大量次优轨迹使 AntMaze 任务极具挑战性，需稳定且强效的 Q 学习才能实现良好性能（例如，基于 BC 的方法在 "medium" 和 "large" 子任务中易失败）。实验表明，在条件扩散模型训练阶段注入 Q 学习引导的设计稳定有效：通过合理设置 η \eta η，Diffusion-QL 显著优于现有方法，尤其在 "large-diverse" 等更难的子任务中表现突出。

Adroit 与 Kitchen 任务域结果

------ Adroit 任务域 ：由于人类示范数据的狭窄性，需强策略正则化以克服离线强化学习中的外推误差（Fujimoto 等人，2019）。Diffusion-QL 通过设置较小的(\eta)，凭借基于逆扩散的策略（兼具强表达能力与更优的策略正则化效果），轻松超越其他基线方法；

------- Kitchen 任务域：该任务需长期价值优化，实验表明 Diffusion-QL 在该领域同样表现优异。

消融实验

为量化分析 Diffusion-QL 在 D4RL 任务上优于其他策略约束类方法的原因，我们对其两大核心组件（扩散模型作为强表达能力策略 、Q 学习引导）开展消融实验：

策略部分：将扩散模型与常用的 CVAE 模型在行为克隆任务中对比；
Q 学习组件：在策略改进阶段与 BCQ 方法对比。

实验结果如表 2 所示：

BC-Diffusion（仅扩散模型行为克隆） 优于BC-CVAE（仅 CVAE 行为克隆），验证了基于扩散的策略具有更强的表达能力，能更好地捕捉数据分布（与图 1 的结论一致）；
在 BCQ 框架下（明确限制策略动作样本与克隆动作样本的偏差范围），BCQ-Diffusion 仍优于BCQ-CVAE------BCQ 对偏差的硬性物理约束实际上限制了策略改进空间，而 Diffusion-QL 通过添加 Q 学习引导进一步提升了性能；
CVAE-QL（CVAE + 自由 Q 学习引导） 表现不佳，表明 CVAE 的弱表达能力与较差的克隆效果，使其难以与无约束的 Q 学习引导有效结合。

综上，消融实验验证了 Diffusion-QL 的两大核心组件协同作用，是其取得优异性能的关键。

结论

本文提出了一种基于条件扩散模型的离线强化学习算法 ------Diffusion-QL。该算法的核心设计包含两部分：首先，其策略通过条件扩散模型的逆扩散链构建 ，该策略类具有极强的表达能力，且模型的学习过程本身即为一种强效的策略正则化方式 ；其次，通过联合学习的 Q 值函数将 Q 学习引导信号注入扩散策略的训练过程，引导去噪采样在已探索区域内朝向最优动作区域收敛。上述两大核心组件的协同作用，使 Diffusion-QL 在 D4RL 基准测试集的所有任务中均实现了当前最优性能。

代码框架

https://github.com/zhendong-wang/diffusion-policies-for-offline-rl

主程序入口 (main.py)

解析命令行参数（环境、超参数、设备等）
加载 D4RL 数据集
创建并训练 agent（Diffusion-QL 或 Diffusion-BC）
定期评估并记录结果
支持在线/离线模型选择

智能体模块 (agents/)

agents/diffusion.py - 扩散模型核心

（1）前向扩散：q_sample() 将动作逐步加噪

（2）反向去噪：p_sample() 逐步生成动作

（3）采样：sample() 从噪声生成动作序列

（4）支持线性/余弦/VP 三种 beta 调度
agents/model.py - 神经网络模型

（1）MLP：去噪网络的 MLP

（2）时间嵌入（正弦位置编码）

（3）状态条件输入

（4）输出去噪后的动作
agents/ql_diffusion.py - Diffusion-Q-Learning

结合 Q-Learning 的扩散策略
agents/bc_diffusion.py - Diffusion Behavior Cloning

纯行为克隆（不包含 Q-Learning）

仅训练扩散模型模仿离线数据

用于对比实验
agents/helpers.py - 辅助工具

时间嵌入：SinusoidalPosEmb

Beta 调度：linear_beta_schedule, cosine_beta_schedule, vp_beta_schedule

损失函数：WeightedL1, WeightedL2

EMA：指数移动平均更新

工具模块 (utils/)

utils/data_sampler.py - 数据采样器
加载 D4RL 数据集
批量采样 (state, action, next_state, reward, done)
奖励调整：normalize、iql_antmaze、cql_antmaze 等
utils/logger.py - 日志系统
实验日志、CSV 记录、模型快照
表格输出格式化
utils/utils.py - 通用工具
进度条：Progress
早停：EarlyStopping
打印横幅

toy_experiments/
用于概念验证的 2D 多模态示例：
run_toy_bc.py - BC 对比实验
生成 4 个角落的多模态数据
对比：
BC-MLE（最大似然估计）
BC-CVAE（条件 VAE）
BC-MMD（最大均值差异）
BC-Diffusion（扩散模型）
可视化生成的动作分布

run_toy_ql.py - Q-Learning 对比实验
添加奖励信号的多模态数据
对比：
TD3+BC（QL-MLE）
BCQ（QL-CVAE）
BEAR-MMD（QL-MMD）
Diffusion-QL（扩散 Q 学习）
展示扩散模型在离线 RL 中捕获多模态与利用 Q 值的能力
toy_experiments/diffusion.py - 玩具实验的扩散实现
扩展了 agents/diffusion.py
包含 guided_sample()：使用 Q 函数梯度引导采样
实验性采样方法