
🔥草莓熊Lotso: 个人主页
❄️个人专栏: 《C++知识分享》 《Linux 入门到实践:零基础也能懂》
✨生活是默默的坚持,毅力是永久的享受!
🎬 博主简介:

文章目录
- 前言:
- [一. 先搞懂基础:Stack 与 Queue 的核心特性](#一. 先搞懂基础:Stack 与 Queue 的核心特性)
- [二. Stack(栈):后进先出(LIFO)的容器](#二. Stack(栈):后进先出(LIFO)的容器)
-
- [2.1 核心特性:](#2.1 核心特性:)
- [2.2 头文件与定义](#2.2 头文件与定义)
- [2.3 常用接口全解析](#2.3 常用接口全解析)
- [2.4 基础用法演示](#2.4 基础用法演示)
- [三. Queue(队列):先进先出(FIFO)的容器](#三. Queue(队列):先进先出(FIFO)的容器)
-
- [3.1 核心特性:](#3.1 核心特性:)
- [3.2 头文件与定义:](#3.2 头文件与定义:)
- [3.3 常用接口全解析](#3.3 常用接口全解析)
- [3.4 基础用法演示](#3.4 基础用法演示)
- [四. 实战练习题](#四. 实战练习题)
-
- [4.1 最小栈](#4.1 最小栈)
- [4.2 栈的压入、弹出序列](#4.2 栈的压入、弹出序列)
- [4.3 逆波兰表达式求值](#4.3 逆波兰表达式求值)
- [4.4 二叉树的层序遍历](#4.4 二叉树的层序遍历)
- 结尾:
前言:
stack(栈)和queue(队列)是 C++ 标准库中两种常用的适配器容器,它们的核心价值在于提供严格的数据访问规则(后进先出 / 先进先出),广泛应用于算法设计和业务逻辑实现。本文聚焦 "实际使用",通过清晰的接口说明和场景示例,帮你快速掌握这两种容器的用法。

一. 先搞懂基础:Stack 与 Queue 的核心特性
在写代码前,首先要明确两者的 "数据访问规则"------ 这是它们区别于其他容器的关键:
| 容器 | 核心规则 | 访问特性 | 适用场景 |
|---|---|---|---|
stack |
后进先出(LIFO) | 仅能访问"栈顶"元素 | 函数调用栈、表达式求值、撤销操作 |
queue |
先进先出(FIFO) | 仅能访问"队头"和"队尾"元素 | 任务调度、消息队列、广度优先搜索(BFS) |
两者的共性是 "限制访问":不支持随机访问(如 [] 下标),也不支持迭代器遍历 ------ 目的是强制遵循其数据规则,避免错误的访问方式
二. Stack(栈):后进先出(LIFO)的容器
2.1 核心特性:
- 访问规则:只能从"栈顶"添加或删除元素(最后入栈的元素最先出栈)
- 适用场景:函数调用栈,表达式求值等。
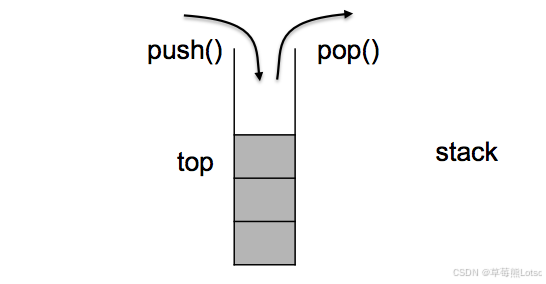
参考文档 :stack - C++ Reference
2.2 头文件与定义
cpp
#include <stack> // 必须包含头文件
using namespace std;
// 定义栈:默认存储int类型,底层依赖deque实现
stack<int> st;
// 可指定底层容器(如vector、list)
stack<int, vector<int>> st_v; // 基于vector的栈
stack<int, list<int>> st_l; // 基于list的栈2.3 常用接口全解析
| 接口 | 功能描述 | 示例 |
|---|---|---|
push(val) |
向栈顶添加元素,新元素成为新的栈顶 | st.push(10); |
pop() |
删除当前栈顶元素(操作后原栈顶的下一个元素成为新栈顶),无返回值,需先确保栈非空 | st.pop(); |
top() |
返回栈顶元素的引用(可直接读取或修改栈顶值),需先确保栈非空 | int x = st.top();(读取);st.top() = 20;(修改) |
size() |
返回栈中当前存储的元素总个数,返回值为无符号整数(size_t) |
cout << st.size(); |
empty() |
判断栈是否为空,若栈中无元素则返回 true,否则返回 false |
if (st.empty()) { ... } |
2.4 基础用法演示
cpp
void test_stack()
{
stack<int> st;
st.push(1);
st.push(2);
st.push(3);
st.emplace(4);
while (!st.empty())
{
cout << st.top() << " ";
st.pop();
}
cout << endl;
}
int main()
{
test_stack();
}
三. Queue(队列):先进先出(FIFO)的容器
3.1 核心特性:
- 访问规则:从"队尾"添加元素,从"队头"删除元素(最先入队的元素最先出队)
- 适用场景:任务调度(如打印队列)、消息队列、广度优先搜索(BFS)等
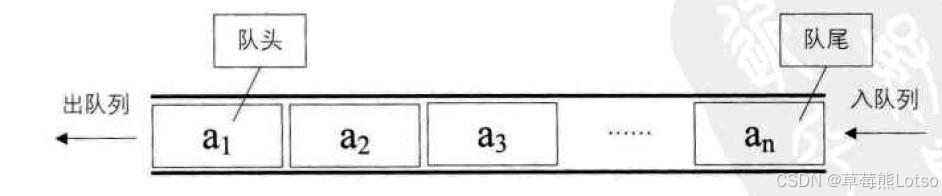
参考文档 :queue - C++ Reference
3.2 头文件与定义:
cpp
#include <queue> // 必须包含的头文件
using namespace std;
// 定义队列:默认底层依赖deque实现
queue<int> q;
// 可指定底层容器(如list,不建议用vector,因vector头删效率低)
queue<int, list<int>> q_l; // 基于list的队列3.3 常用接口全解析
| 接口 | 功能描述 | 示例 |
|---|---|---|
push(val) |
向队列的队尾添加一个元素,新元素成为队列的最后一个元素,操作后队列长度+1 | q.push("任务1"); |
pop() |
删除队列的队头 元素(即最早入队的元素),操作后队列长度-1,无返回值 (需先通过 front() 获取队头元素再删除) |
q.pop(); |
front() |
返回队列队头元素的引用(可读取或修改),仅访问不删除,需确保队列非空 | string task = q.front();(读取);q.front() = "优先任务1";(修改) |
back() |
返回队列队尾元素的引用(可读取或修改),仅访问不删除,需确保队列非空 | string last = q.back();(读取);q.back() = "最后任务";(修改) |
size() |
返回队列中当前存储的元素总个数,返回值类型为 size_t(无符号整数) |
cout << q.size(); |
empty() |
判断队列是否为空:若队列中无元素则返回 true,有元素则返回 false,常用于遍历或删除前判断队列状态 |
if (q.empty()) { cout << "队列为空"; } |
3.4 基础用法演示
cpp
void test_queue()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.emplace(4);
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
int main()
{
//test_stack();
test_queue();
}
四. 实战练习题
4.1 最小栈
题目链接:
题目描述 :

题目示例 :

C++算法代码:
cpp
class MinStack {
public:
MinStack() {
//可以啥都不写,甚至可以删掉
//会去调这个自定义类型的默认构造
}
void push(int val) {
_st.push(val);
if(_minst.empty()||_minst.top()>=val)
_minst.push(val);
}
void pop() {
if(_minst.top()==_st.top())
_minst.pop();
_st.pop();
}
int top() {
return _st.top();
}
int getMin() {
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/图解 :
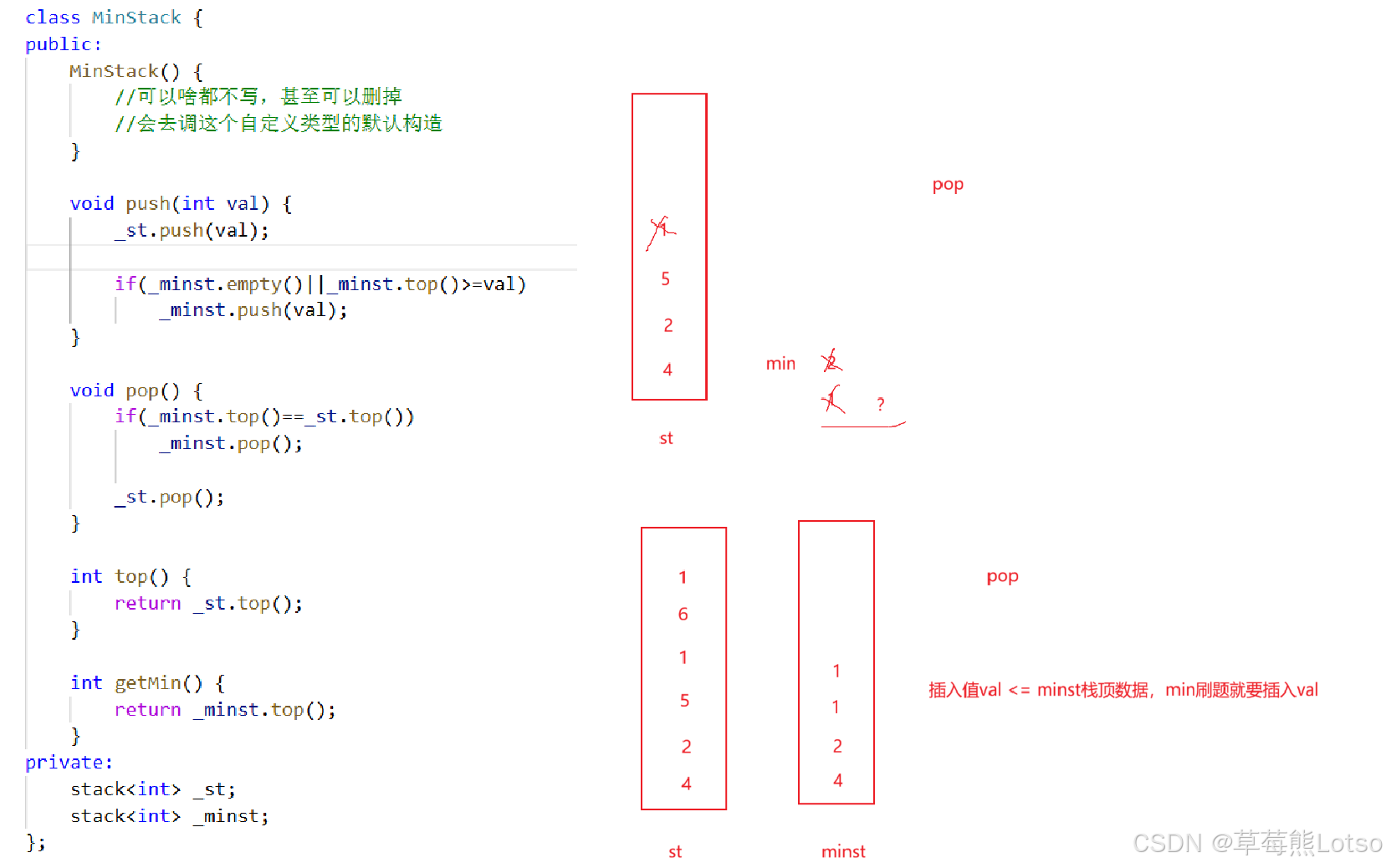
4.2 栈的压入、弹出序列
题目链接:
题目描述 :
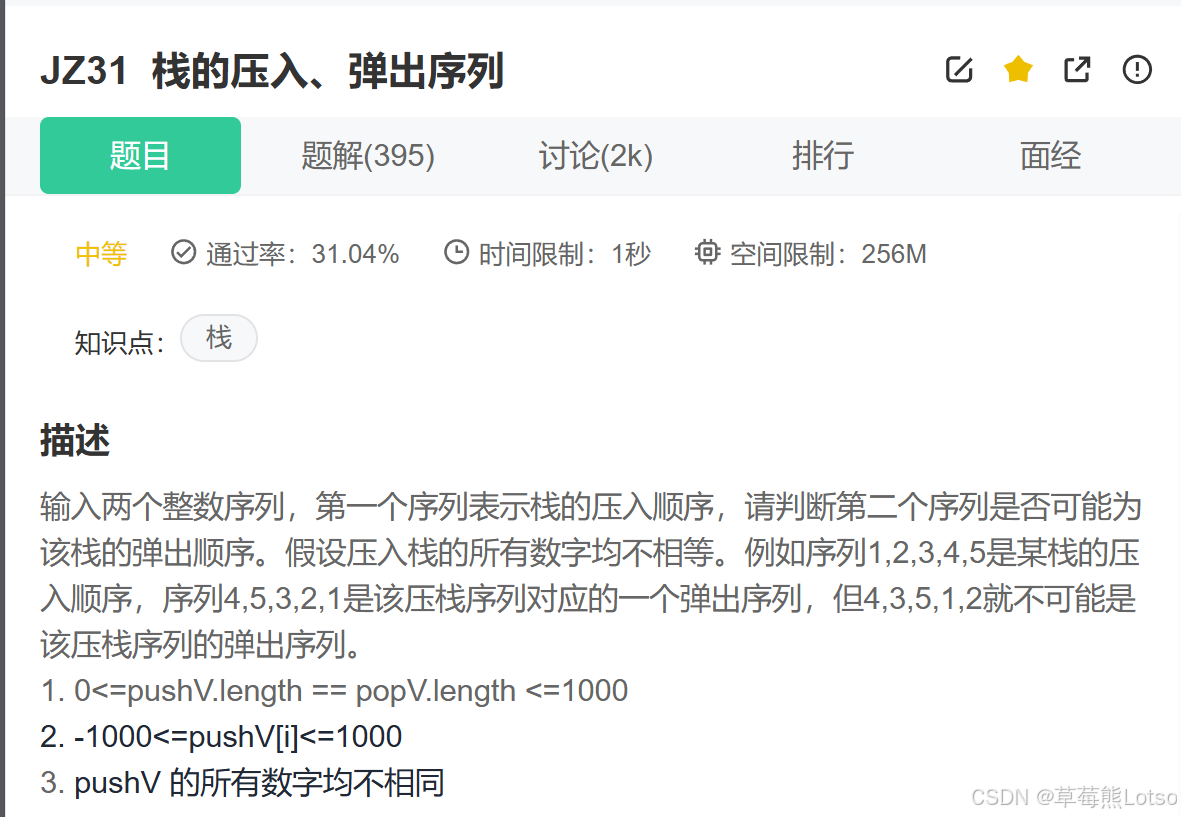
题目示例 :

C++算法代码:
cpp
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
int pushi=0,popi=0;
stack<int> st;
while(pushi<pushV.size())
{
st.push(pushV[pushi]);
while(!st.empty()&&st.top()==popV[popi])
{
st.pop();
popi++;
}
pushi++;
}
return st.empty();
}
};图解 :

4.3 逆波兰表达式求值
题目链接:
题目描述 :

题目示例 :

补充说明 :

C++算法代码:
cpp
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto& str:tokens)
{
if(str=="+"||str=="-"||str=="*"||str=="/")
{
//运算符
int right=st.top();
st.pop();
int left=st.top();
st.pop();
switch(str[0])
{
case '+':
st.push(left+right);
break;
case '-':
st.push(left-right);
break;
case '*':
st.push(left*right);
break;
case '/':
st.push(left/right);
break;
}
}
else{
//运算数
st.push(stoi(str));
}
}
return st.top();
}
};图解 :

4.4 二叉树的层序遍历
题目链接:
题目描述 :
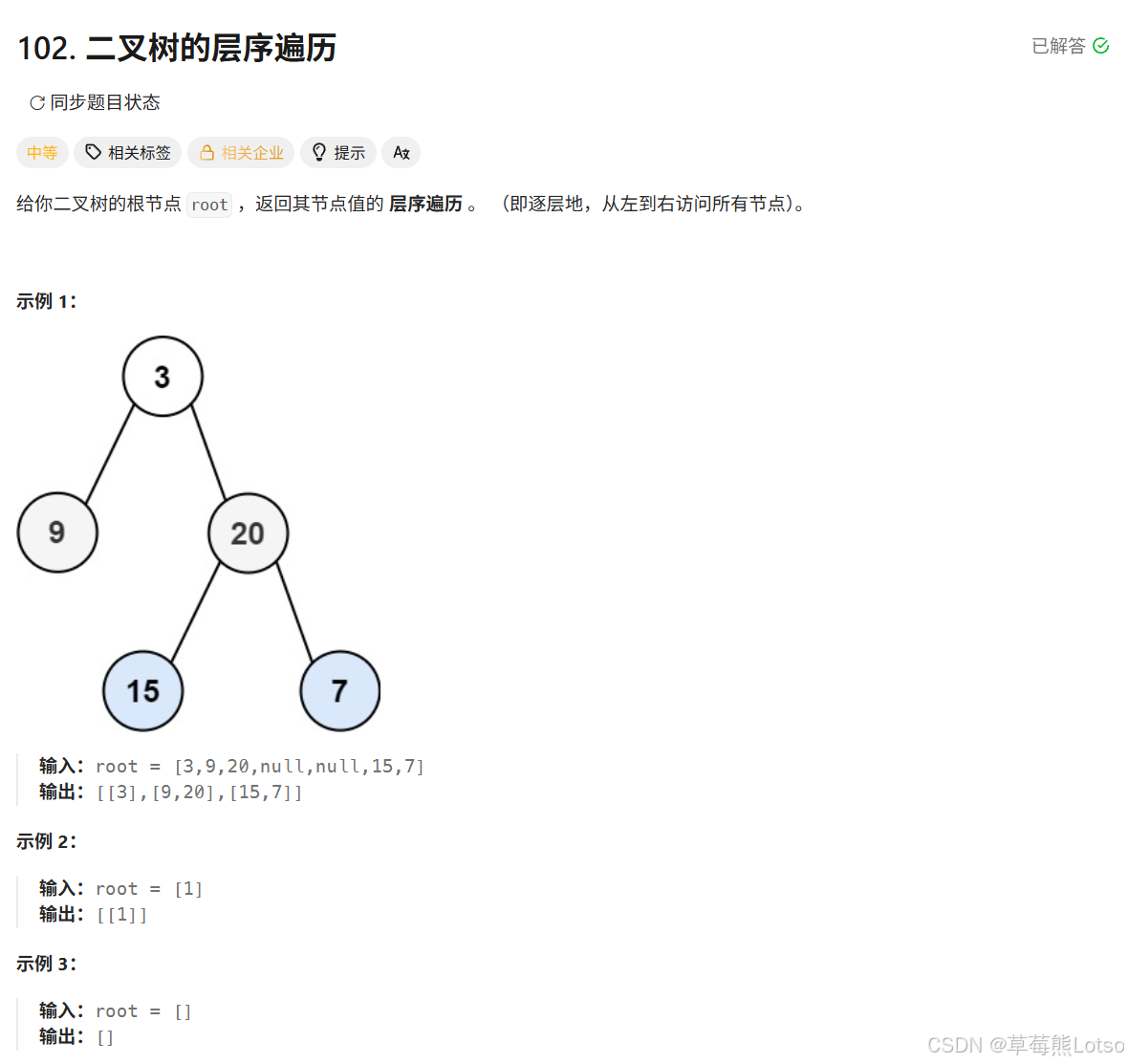
题目示例 :
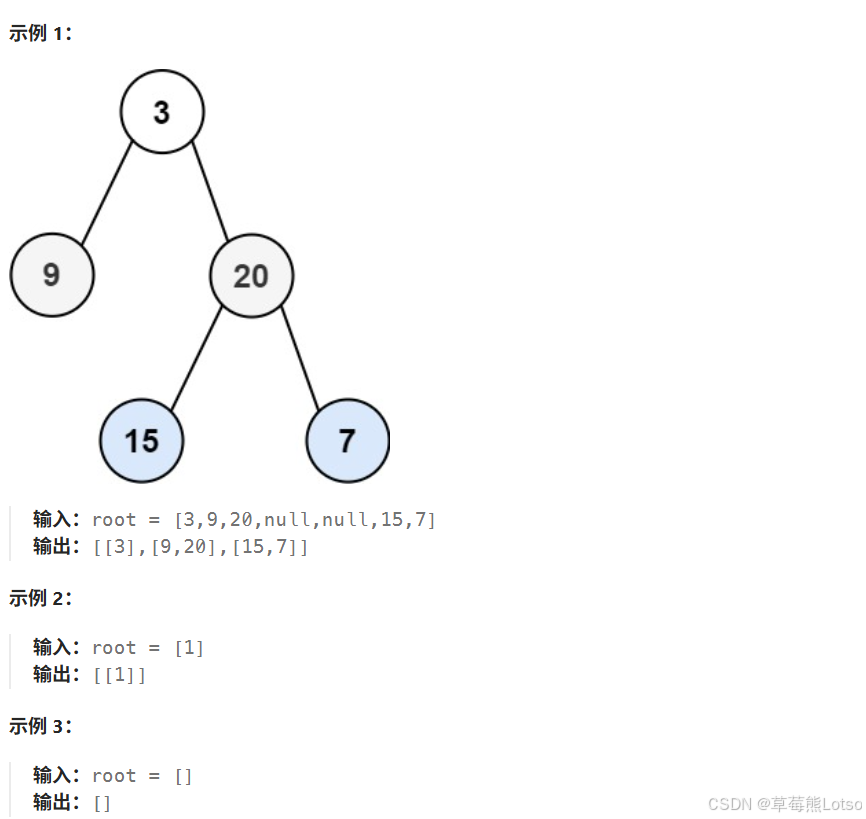
C++算法代码:
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
int levelSize=0;
if(root)
{
q.push(root);
levelSize=1;
}
vector<vector<int>> vv;
while(!q.empty())
{
vector<int> v;
//一层一层的出
while(levelSize--)
{
TreeNode* front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
q.push(front->left);
if(front->right)
q.push(front->right);
}
vv.push_back(v);
//现在的leveSize等于当前队列的size
levelSize=q.size();
}
return vv;
}
};图解 :
每次只出当前层的元素,出之前把它的左右孩子插入栈中,等到当前层的出完出去之后更新levelSize,此时刚好等于现在栈中的元素个数。

结尾:
往期回顾:
C++ 手写 List 容器实战:从双向链表原理到完整功能落地,附源码与测试验证
结语:Stack 和 Queue 作为 C++ 标准库中经典的适配器容器,凭借明确的访问规则在各类场景中发光发热。掌握它们的基础操作,再结合实战习题打磨,就能轻松应对算法与业务中的数据管理需求,快去实践吧~
✨把这些内容吃透超牛的!放松下吧✨ ʕ˘ᴥ˘ʔ づきらど
