封装红黑树实现mymap和myset

1. 源码及框架分析

SGI-STL30版本源代码，map和set的源代码在map/set/stl_map.h/stl_set.h/stl_tree.h等⼏个头⽂件 中。 map和set的实现结构框架核⼼部分截取出来如下：

// set
#ifndef __SGI_STL_INTERNAL_TREE_H
#include <stl_tree.h>
#endif
#include <stl_set.h>
#include <stl_multiset.h>
// map
#ifndef __SGI_STL_INTERNAL_TREE_H
#include <stl_tree.h>
#endif
#include <stl_map.h>
#include <stl_multimap.h>

// stl_set.h
template <class Key, class Compare = less<Key>, class Alloc = alloc>
class set {
public:
 // typedefs:
 typedef Key key_type;
 typedef Key value_type;
private:
 typedef rb_tree<key_type, value_type, 
 identity<value_type>, key_compare, Alloc> rep_type;
 rep_type t; // red-black tree representing set
};

// stl_map.h
template <class Key, class T, class Compare = less<Key>, class Alloc = alloc>
class map {
public:
// typedefs:
 typedef Key key_type;
 typedef T mapped_type;
typedef pair<const Key, T> value_type;
private:
 typedef rb_tree<key_type, value_type, 
 select1st<value_type>, key_compare, Alloc> rep_type;
 rep_type t; // red-black tree representing map
};

// stl_tree.h：rb_tree
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc 
= alloc>
class rb_tree {
protected:
 typedef void* void_pointer;
 typedef __rb_tree_node_base* base_ptr;
 typedef __rb_tree_node<Value> rb_tree_node;
 typedef rb_tree_node* link_type;
 typedef Key key_type;
 typedef Value value_type;
public:
 // insert⽤的是第⼆个模板参数左形参 
 pair<iterator,bool> insert_unique(const value_type& x);
 
 // erase和find⽤第⼀个模板参数做形参 
 size_type erase(const key_type& x);
 iterator find(const key_type& x);
protected:
 size_type node_count; // keeps track of size of tree
 link_type header;
};

// __rb_tree_node_base
struct __rb_tree_node_base
{
 typedef __rb_tree_color_type color_type;
 typedef __rb_tree_node_base* base_ptr;
 color_type color; 
 base_ptr parent;
 base_ptr left;
 base_ptr right;
};

// __rb_tree_node
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
 typedef __rb_tree_node<Value>* link_type;
 Value value_field;
};

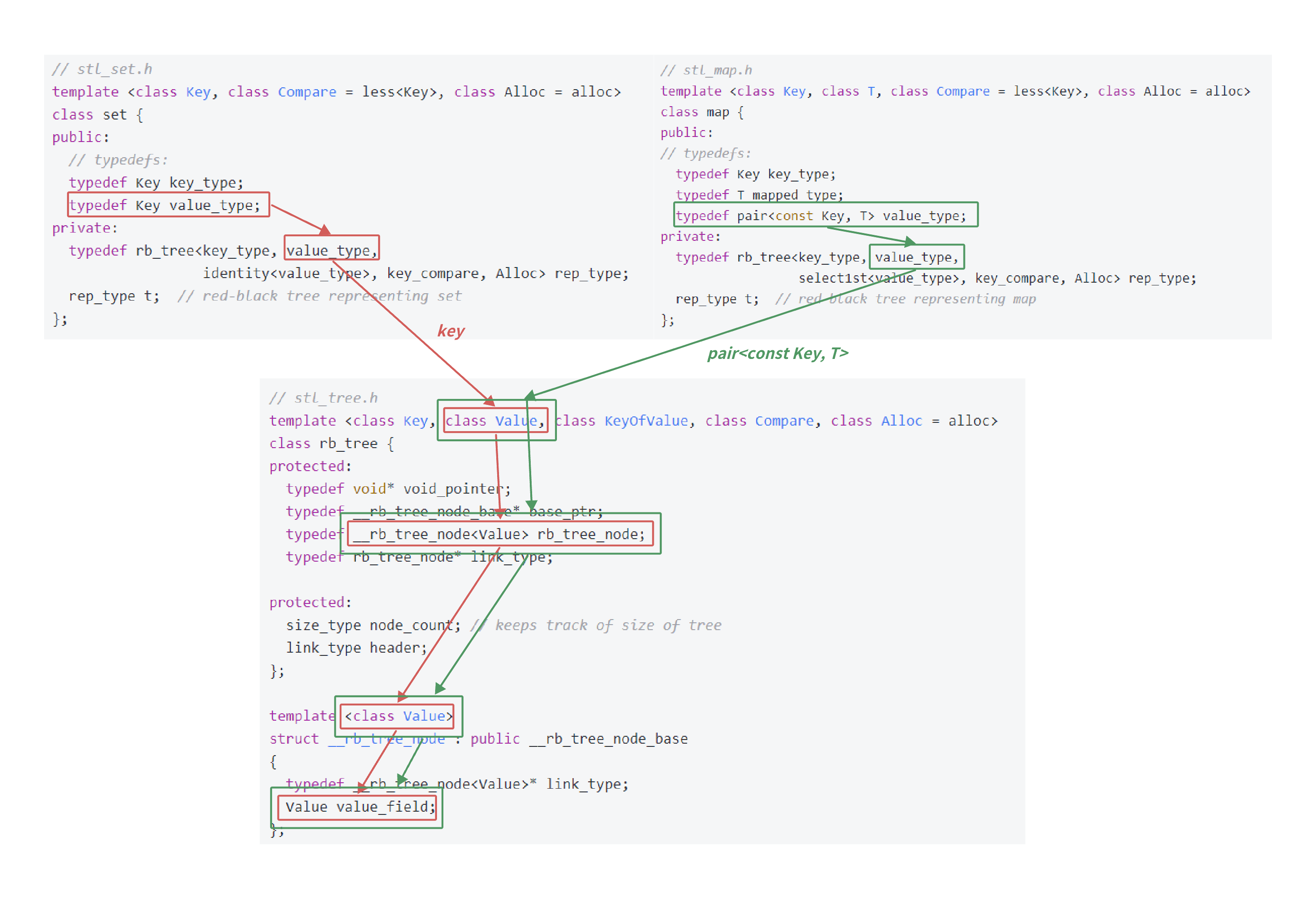
• 通过下图对框架的分析，我们可以看到源码中rb_tree⽤了⼀个巧妙的泛型思想实现，rb_tree是实现key的搜索场景，还是key/value的搜索场景不是直接写死的，⽽是由第⼆个模板参数Value决定 _rb_tree_node中存储的数据类型。如果是key的搜索场景，给_rb_tree_node传的是key，如果是key/value的搜索场景，给_rb_tree_node传的是pair

• set实例化rb_tree时第⼆个模板参数给的是key，map实例化rb_tree时第⼆个模板参数给的是 pair，这样⼀颗红⿊树既可以实现key搜索场景的set，也可以实现key/value搜索场 景的map。

• 要注意⼀下，源码⾥⾯模板参数是⽤T代表value，⽽内部写的value_type不是我们我们⽇常 key/value场景中说的value，源码中的value_type反⽽是红⿊树结点中存储的真实的数据的类型。

• rb_tree第⼆个模板参数Value已经控制了红⿊树结点中存储的数据类型，为什么还要传第⼀个模板 参数Key呢？尤其是set，两个模板参数是⼀样的，这是很多同学这时的⼀个疑问。要注意的是对于 map和set，find/erase时的函数参数都是Key，所以第⼀个模板参数是传给find/erase等函数做形 参的类型的。对于set⽽⾔两个参数是⼀样的，但是对于map⽽⾔就完全不⼀样了，map insert的 是pair对象，但是find和ease的是Key对象。

• 吐槽⼀下，这⾥源码命名⻛格⽐较乱，set模板参数⽤的Key命名，map⽤的是Key和T命名，⽽ rb_tree⽤的⼜是Key和Value，可⻅⼤佬有时写代码也不规范，乱弹琴。

2. 模拟实现map和set

2.1 实现出复⽤红⿊树的框架，并⽀持insert

• 参考源码框架，map和set复⽤之前我们实现的红⿊树。

• 我们这⾥相⽐源码调整⼀下，key参数就⽤K，value参数就⽤V，红⿊树中的数据类型，我们使⽤ T。

• 其次因为RBTree实现了泛型不知道T参数是K，还是pair，那么insert内部进⾏插⼊逻辑 ⽐较时，就没办法进⾏⽐较，因为pair的默认⽀持的是key和value⼀起参与⽐较，我们需要时的任 何时候只⽐较key，所以我们在map和set层分别实现⼀个MapKeyOfT和SetKeyOfT的仿函数传给 RBTree的KeyOfT，然后RBTree中通过KeyOfT仿函数取出T类型对象中的key，再进⾏⽐较，具体 细节参考如下代码实现。

template<class K>
class set
{
	struct SetKeyOfT
	{
		// K是元素的key的类型
		const K& operator()(const K& k)
		{
			return k;
		}
	};

public:
	bool insert(const K& k)
	{
		return _t.Insert(k);
	}
	
private:
	RBTree<K, const K, SetKeyOfT> _t;
	};

template<class K, class V>
class map
{
	struct MapKeyOfT
	{
		// K是元素的key的类型
		const K& operator()(const pair<K,V>& kv)
		{
			return kv.first;
		}
	};
public:
	
	bool insert(const pair<const K, V>& kv)
	{
		return _t.Insert(kv);
	}

private:
	RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};

// 红黑树的插入
bool Insert(const T& data)
{
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_col = BLACK;
		return true;
	}

	KeyOfT kot;
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (kot(cur->_data) > kot(data))
		{
			parent = cur;
			cur = cur->_left;
		}
		else if (kot(cur->_data) < kot(data))
		{
			parent = cur;
			cur = cur->_right;
		}
		// 不允许插入相同key值
		else
		{
			return false;
		}
	}

2.2 ⽀持iterator的实现

iterator实现思路分析

• iterator实现的⼤框架跟list的iterator思路是⼀致的，⽤⼀个类型封装结点的指针，再通过重载运算 符实现，迭代器像指针⼀样访问的⾏为。

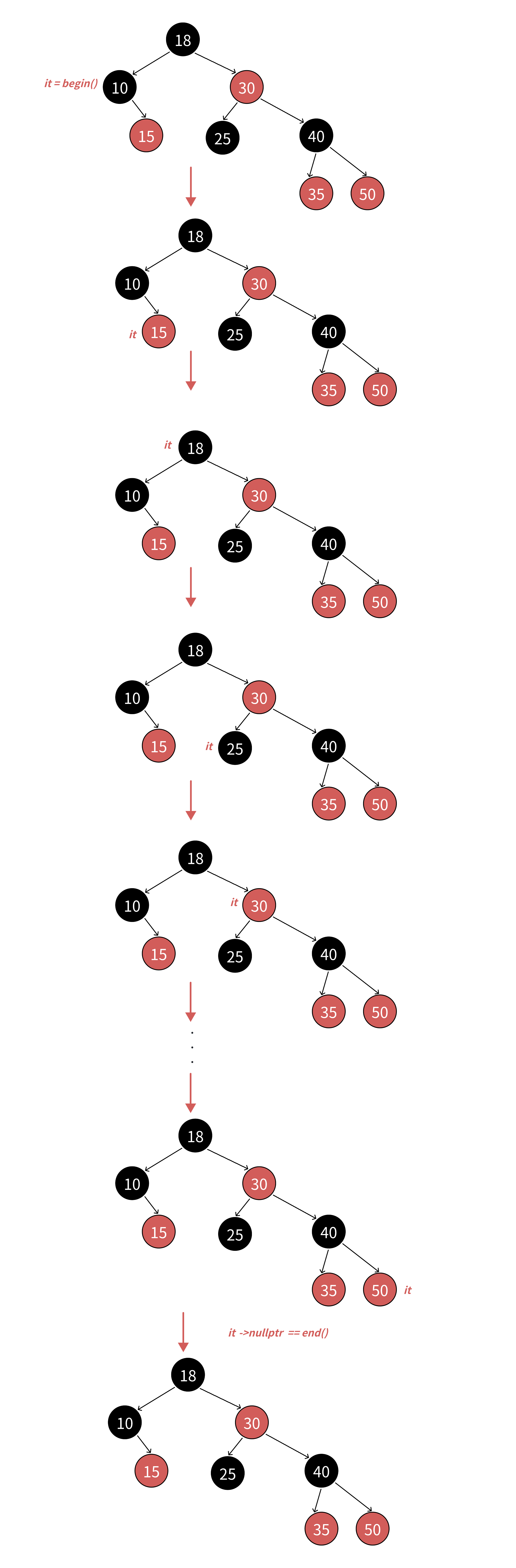
• 这⾥的难点是operator++和operator--的实现。之前使⽤部分，我们分析了，map和set的迭代器⾛ 的是中序遍历，左⼦树->根结点->右⼦树，那么begin()会返回中序第⼀个结点的iterator也就是10 所在结点的迭代器。

• 迭代器++的核⼼逻辑就是不看全局，只看局部，只考虑当前中序局部要访问的下⼀个结点。

• 迭代器++时，如果it指向的结点的右⼦树不为空，代表当前结点已经访问完了，要访问下⼀个结点 是右⼦树的中序第⼀个，⼀棵树中序第⼀个是最左结点，所以直接找右⼦树的最左结点即可。

• 迭代器++时，如果it指向的结点的右⼦树空，代表当前结点已经访问完了且当前结点所在的⼦树也 访问完了，要访问的下⼀个结点在当前结点的祖先⾥⾯，所以要沿着当前结点到根的祖先路径向上 找。

• 如果当前结点是⽗亲的左，根据中序左⼦树->根结点->右⼦树，那么下⼀个访问的结点就是当前结 点的⽗亲；如下图：it指向25，25右为空，25是30的左，所以下⼀个访问的结点就是30。

• 如果当前结点是⽗亲的右，根据中序左⼦树->根结点->右⼦树，当前当前结点所在的⼦树访问完 了，当前结点所在⽗亲的⼦树也访问完了，那么下⼀个访问的需要继续往根的祖先中去找，直到找 到孩⼦是⽗亲左的那个祖先就是中序要问题的下⼀个结点。如下图：it指向15，15右为空，15是10 的右，15所在⼦树话访问完了，10所在⼦树也访问完了，继续往上找，10是18的左，那么下⼀个 访问的结点就是18。

• end()如何表⽰呢？如下图：当it指向50时，++it时，50是40的右，40是30的右，30是18的右，18 到根没有⽗亲，没有找到孩⼦是⽗亲左的那个祖先，这是⽗亲为空了，那我们就把it中的结点指针 置为nullptr，我们⽤nullptr去充当end。需要注意的是stl源码空，红⿊树增加了⼀个哨兵位头结点 做为end()，这哨兵位头结点和根互为⽗亲，左指向最左结点，右指向最右结点。相⽐我们⽤ nullptr作为end()，差别不⼤，他能实现的，我们也能实现。只是--end()判断到结点时空，特殊处 理⼀下，让迭代器结点指向最右结点。具体参考迭代器--实现。

• 迭代器--的实现跟++的思路完全类似，逻辑正好反过来即可，因为他访问顺序是右⼦树->根结点-> 左⼦树，具体参考下⾯代码实现。

• set的iterator也不⽀持修改，我们把set的第⼆个模板参数改成const K即可， RBTreeconst K, SetKeyOfT> _t;

• map的iterator不⽀持修改key但是可以修改value，我们把map的第⼆个模板参数pair的第⼀个参 数改成constK即可， RBTreepair, MapKeyOfT> _t;

• ⽀持完整的迭代器还有很多细节需要修改，具体参考下⾯题的代码。
总结：

1.begin()就是红黑树的最左节点。

2.end()就是nullptr

3.operator++

a.如果右子树不为空，中序的下一个是右子树的最左(最小)节点。

b.如果右子树为空，中序的下一个是祖先中孩子是父亲左边的那个节点。

4.operator--

a.如果左子树不为空，中序的下一个是左子树的最右(最大)节点。

b.如果左子树为空，中序的下一个是祖先中孩子是父亲右边的那个节点。

c.如果节点为空，说明迭代器走到end()或者是空树，如果走到end()，end()--就是找红黑树中序的最后一个，即红黑树的最右节点。

2.3 map⽀持[]

• map要⽀持[]主要需要修改insert返回值⽀持，修改RBtree中的insert返回值为pair<Iterator,bool> Insert(const T& data)。

a.key已经存在时，operator[]充当查找+修改的功能，pair的first是那个已经存在的key节点的迭代器，second是false。

b.key不存在时，operator[]充当插入+修改的功能，pair的first是那个新插入节点的迭代器，second是true。

• 有了insert⽀持[]实现就很简单了，具体参考下⾯代码实现

2.4 Mymap和Myset代码实现

// Myset.h
#include"RBTree.h"

namespace wsj
{
	template<class K>
	class set
	{
		struct SetKeyOfT
		{
			// K是元素的key的类型
			const K& operator()(const K& k)
			{
				return k;
			}
		};
	public:
		typedef  typename RBTree<K, const K, SetKeyOfT>::Iterator iterator;
		typedef  typename RBTree<K, const K, SetKeyOfT>::Const_Iterator const_iterator;

		iterator begin()
		{
			return _t.Begin();
		}

		iterator end()
		{
			return _t.End();
		}

		const_iterator begin() const
		{
			return _t.Begin();
		}

		const_iterator end() const
		{
			return _t.End();
		}

		pair<iterator,bool> insert(const K& k)
		{
			return _t.Insert(k);
		}

	private:
		RBTree<K, const K, SetKeyOfT> _t;
	};
}

// Mymap.h
#include"RBTree.h"

namespace wsj
{
	template<class K, class V>
	class map
	{
		struct MapKeyOfT
		{
			// K是元素的key的类型
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef  typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;
		typedef  typename RBTree<K, pair<const K, V>, MapKeyOfT>::Const_Iterator const_iterator;

		iterator begin()
		{
			return _t.Begin();
		}

		iterator end()
		{
			return _t.End();
		}

		const_iterator begin() const
		{
			return _t.Begin();
		}

		const_iterator end() const
		{
			return _t.End();
		}

		pair<iterator,bool> insert(const pair<const K, V>& kv)
		{
			return _t.Insert(kv);
		}

		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert({ key,V() });
			return ret.first->second;
		}

	private:
		RBTree<K, pair<const K, V>, MapKeyOfT> _t;
	};
}

2.5 RBTreeIterator(迭代器)部分实现

// template<class T,class T&,class T*>
template<class T,class Ref,class Ptr>
class RBTreeIterator
{
public:
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T, Ref, Ptr> Self;

	// _node是节点的指针
	// _root是根节点的指针，用于迭代器走到end()时--查找红黑树的最右节点
	Node* _node;
	Node* _root;
	RBTreeIterator(Node* node, Node* root)
		:_node(node)
		,_root(root)
	{}

	// ++返回的是迭代器
	Self operator++()
	{
		if (_node->_right)
		{
			// 右不为空，中序的下一个是右子树的最左(最小)节点
			Node* cur = _node->_right;
			while (cur->_left)
			{
				cur = cur->_left;
			}
			_node = cur;
		}
		else
		{
			// 右为空,下一个是祖先中孩子是父亲左节点的那个
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}

		// this是指向自身(RBTreeIterator)的指针
		return *this;
	}

	// --返回的是迭代器
	Self operator--()
	{
		if(_node==nullptr)
		{
			// end()的前一个是红黑树的最右节点
			Node* cur = _root;
			while (cur->_right)
			{
				cur = cur->_right;
			}
			_node = cur;
		}
		else if (_node->_left)
		{
			// 左不为空，中序的上一个是左子树的最右(最大)节点
			Node* cur = _node->_left;
			while (cur->_right)
			{
				cur = cur->_right;
			}
			_node = cur;
		}
		else
		{
			// 左为空,下一个是祖先中孩子是父亲右节点的那个
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = parent;
				parent = cur->_parent;
			}
			_node = parent;
		}

		// this是指向自身(RBTreeIterator)的指针
		return *this;
	}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &_node->_data;
	}

	bool operator!=(const Self& s) const
	{
		return _node != s._node;
	}

	bool operator==(const Self& s) const
	{
		return _node == s._node;
	}
};

2.6 RBTree部分实现

#include<iostream>
using namespace std;


// 枚举红黑树的颜色
enum Color
{
	RED,
	BLACK
};

// 红黑数节点
template<class T>
struct RBTreeNode
{
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	Color _col;

	// 默认构造
	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};

// 红黑树结构
// K:是元素的key的类型，用于find/erase操作
// T:是RBTreeNode里存储的元素类型，用于insert操作
// KeyOfT:是自定义类型，通过operator()返回T类型用于比较的key值
template<class K, class T,class KeyOfT>
class RBTree
{
	typedef RBTreeNode<T> Node;

public:
	typedef RBTreeIterator<T, T&, T*> Iterator;
	typedef RBTreeIterator<T, const T&, T*> Const_Iterator;

	Iterator Begin()
	{
		// begin就是红黑树的最左节点
		Node* cur = _root;
		while (cur->_left)
		{
			cur = cur->_left;
		}

		return Iterator(cur, _root);
	}

	Iterator End()
	{
		return Iterator(nullptr, _root);
	}

	Const_Iterator Begin() const
	{
		// begin就是红黑树的最左节点
		Node* cur = _root;
		while (cur->_left)
		{
			cur = cur->_left;
		}

		return Const_Iterator(cur, _root);
	}

	Const_Iterator End() const
	{
		return Const_Iterator(nullptr, _root);
	}

	// 红黑树的插入
	pair<Iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return { Iterator(_root,_root),true };
		}

		KeyOfT kot;
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			// 不允许插入相同key值
			else
			{
				return { Iterator(cur,_root),false };
			}
		}

		// 新增节点为红色节点
		cur = new Node(data);
		Node* newNode = cur;
		cur->_col = RED;
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		// 如果父亲节点也是红，则需要特殊处理,最坏情况是处理至根节点，最后将根节点变成黑色节点即可
		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			//    g
			// p     u
			if (parent == grandfather->_left)
			{
				Node* uncle = grandfather->_right;
				// 叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 父亲和叔叔变黑，爷爷变红
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					// 变色后继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}

				// 叔叔不存在或者叔叔为黑
				else
				{
					// 以p为旋转点进行右单旋，然后p变黑，g变红,停止更新
					//       g
					//    p     u
					//  c
					if (parent->_left == cur)
					{
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					//        g
					//    p       u
					//      c
					else
					{
						// 先以p为旋转点进行左单旋，再以g节点进行右单旋
						// 然后c变成黑色，g变成红色,停止更新
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			//    g
			// u     p
			else
			{
				Node* uncle = grandfather->_left;
				// 叔叔存在且为红
				if (uncle && uncle->_col == RED)
				{
					// 父亲和叔叔变黑，爷爷变红
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					// 变色后继续向上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				// 叔叔不存在或者叔叔为黑
				else
				{
					// 以p为旋转点进行左单旋，然后p变黑，g变红,停止更新
					//       g
					//    u     p
					//             c
					if (parent->_right == cur)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					//        g
					//    u       p
					//          c
					else
					{
						// 先以p为旋转点进行右单旋，再以g节点进行右单旋
						// 然后c变成黑色，g变成红色,停止更新
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}
		_root->_col = BLACK;

		return { Iterator(newNode,_root),true };
	}

	// 旋转代码的实现跟AVL树是⼀样的，只是不需要更新平衡因⼦
	// 左单旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		Node* pParent = parent->_parent;

		// 把parent变成sunR的左孩子，sunRL变成parent的右孩子
		subR->_left = parent;
		parent->_right = subRL;

		// 改变parent、subR、subRL的_parent
		parent->_parent = subR;
		subR->_parent = pParent;
		if (subRL)
			subRL->_parent = parent;

		// parent有可能是整棵树的根，也可能是局部的子树
		// 如果是整棵树的根，要修改_root
		// 如果是局部的子树，要跟上一层连接
		if (pParent)
		{
			if (pParent->_left == parent)
				pParent->_left = subR;
			else
				pParent->_right = subR;
		}
		else
			_root = subR;
	}

	// 右单旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		Node* pParent = parent->_parent;

		// 将parent变成subL的右边，subLR变成parent的左边
		subL->_right = parent;
		parent->_left = subLR;

		// 改变parent、subL、subLR的_parent
		parent->_parent = subL;
		subL->_parent = pParent;
		if (subLR)
			subLR->_parent = parent;

		// parent有可能是整棵树的根，也可能是局部的子树
		// 如果是整棵树的根，要修改_root
		// 如果是局部的子树，要跟上一层连接
		if (pParent)
		{
			if (pParent->_left == parent)
				pParent->_left = subL;
			else
				pParent->_right = subL;
		}
		else
			_root = subL;
	}

private:
	Node* _root = nullptr;
};