Transformer: LayerNorm层归一化模块详解(PyTorch实现)

🚀 本文将从底层算法原理出发，带你一步步实现一个与 PyTorch 官方版本完全等价的 LayerNorm 模块，帮助你深入理解 Transformer 等现代架构背后的归一化机制。

🧠 一、为什么要自定义 LayerNorm？

在深度学习模型中，归一化 (Normalization) 技术被广泛用于稳定训练和加速收敛。

最早的 Batch Normalization (BN) 虽然高效，但存在两个局限：

对 batch size 敏感；
不适用于 变长序列 或 自回归模型（如 Transformer, RNN）。

为了解决这些问题，Layer Normalization (LayerNorm) 应运而生。

它通过对单个样本的特征维度进行归一化，使模型在不同批量大小和序列长度下都能保持稳定表现。

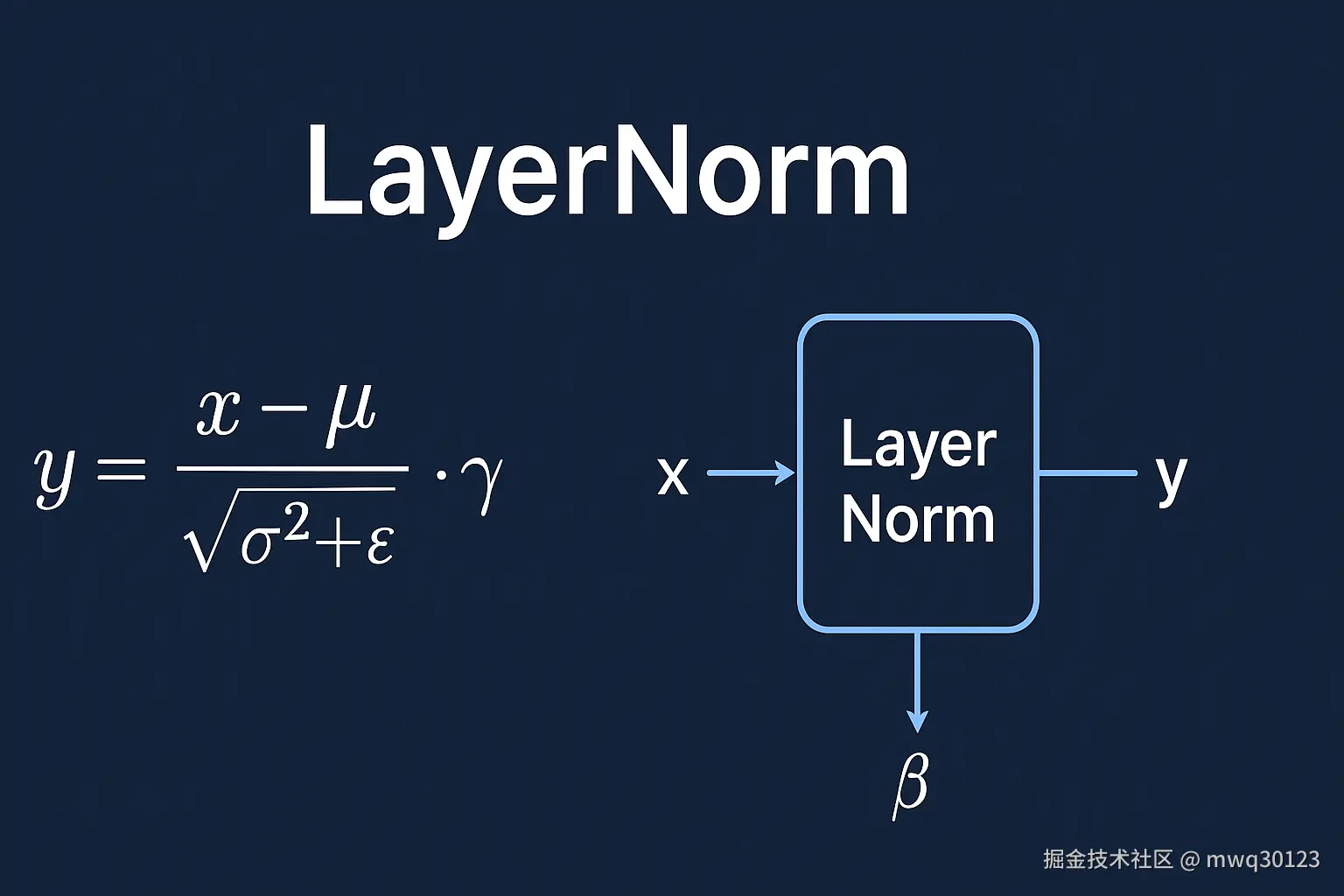
⚙️ 二、LayerNorm 的数学原理

LayerNorm 的计算逻辑非常简洁：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> y = x − μ σ 2 + ϵ ⋅ γ + β y = \frac{x - \mu}{\sqrt{\sigma^2 + \epsilon}} \cdot \gamma + \beta </math>y=σ2+ϵ x−μ⋅γ+β

其中：

符号	含义
x	输入特征向量
mu (μ)	特征维度上的均值
sigma^2 (σ²)	特征维度上的方差
eps (ε)	防止除零的数值稳定项（如 1e-5）
gamma (γ)	可学习的缩放参数（scale）
beta (β)	可学习的偏移参数（shift）

💡 γ 与 β 允许模型学习自适应的缩放与偏移，从而保留归一化前的表达能力。

在某些场景下，它们甚至可以「撤销」归一化带来的影响，让网络拥有更大的自由度。

🧩 三、从零实现一个 PyTorch 版 LayerNorm

下面我们直接用 PyTorch 实现一个等价于 torch.nn.LayerNorm 的模块 👇

python 复制代码

import torch
import torch.nn as nn

class LayerNorm(nn.Module):
    """
    自定义层归一化（Layer Normalization）模块。
    对输入的最后一个维度（特征维度）执行归一化操作。
    """
    def __init__(self, emb_dim: int):
        """
        初始化 LayerNorm 模块。

        参数:
            emb_dim (int): 输入张量的特征维度（最后一维的大小）。
        """
        super().__init__()

        self.eps = 1e-5  # 数值稳定项
        self.scale = nn.Parameter(torch.ones(emb_dim))   # gamma
        self.shift = nn.Parameter(torch.zeros(emb_dim))  # beta

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        前向传播函数。

        参数:
            x (torch.Tensor): 输入张量，形状一般为 (batch_size, seq_len, d_model)
        返回:
            torch.Tensor: 归一化后的输出，形状与输入相同。
        """
        # 1. 计算均值与方差（沿最后一维）
        mean = x.mean(dim=-1, keepdim=True)
        var = x.var(dim=-1, keepdim=True, unbiased=False)

        # 2. 归一化
        norm_x = (x - mean) / torch.sqrt(var + self.eps)

        # 3. 仿射变换
        return self.scale * norm_x + self.shift

✅ 实现要点：

所有计算都在样本内部完成（与 BatchNorm 不同）。
unbiased=False 确保方差计算与官方实现保持一致。
可学习参数 scale 与 shift 分别对应 LayerNorm 中的 γ 与 β。

🔍 四、LayerNorm 的优势与适用场景

优势	说明
训练更稳定	缓解内部协变量偏移，使模型更易收敛。
与批次大小无关	计算完全基于单样本，batch_size=1 也能稳定工作。
更适合序列模型	在 Transformer、RNN、LLM 等模型中效果显著。

尤其在 Transformer Encoder/Decoder 层 中，LayerNorm 是不可或缺的模块之一。

每一层的输入与输出几乎都伴随一次归一化操作。

🧾 五、验证与官方实现的一致性

我们通过以下实验验证自定义版本与官方 torch.nn.LayerNorm 的等价性：

python 复制代码

emb_dim = 128
batch_size = 4
seq_len = 10

# 随机输入
input_tensor = torch.randn(batch_size, seq_len, emb_dim)

# 实例化两个版本
my_ln = LayerNorm(emb_dim)
torch_ln = nn.LayerNorm(emb_dim)

# 同步参数确保公平比较
with torch.no_grad():
    my_ln.scale.copy_(torch_ln.weight)
    my_ln.shift.copy_(torch_ln.bias)

# 输出对比
output_my = my_ln(input_tensor)
output_torch = torch_ln(input_tensor)

# 是否等价
are_equal = torch.allclose(output_my, output_torch)
print(f"输出是否等价: {are_equal}")

运行结果如下：

css 复制代码

输入形状: torch.Size([4, 10, 128])
自定义 LayerNorm 输出形状: torch.Size([4, 10, 128])
官方 LayerNorm 输出形状: torch.Size([4, 10, 128])
输出是否等价: True

✅ 结论：

我们的实现与官方模块在数值上完全等价，仅在底层实现（C++ vs Python）上存在性能差异。

🧮 六、总结

维度	LayerNorm 特点
计算粒度	针对单个样本
是否依赖 batch size	否
是否适用于序列模型	✅ 是
可学习参数	γ（scale），β（shift）
与 BatchNorm 区别	不使用跨样本统计量

LayerNorm 的意义在于：

它让每个 token 的特征分布独立可控，从而使 Transformer 等复杂网络能稳定地进行梯度传播与参数更新。