Transformer : 深度神经网络中的残差连接 (Residual Connection)

Transformer:深度神经网络中的残差连接 (Residual Connection)

1. 概述

随着深度学习的发展，神经网络的深度不断增加，以期获得更强的表达能力。然而，简单的堆叠网络层会导致一个严重的问题------梯度消失 (Vanishing Gradients) ，这使得深层网络的训练变得异常困难。残差连接（Residual Connection） ，也称为快捷连接 (Shortcut Connection) ，由 Kaiming He 等人在其开创性的论文《Deep Residual Learning for Image Recognition》(ResNet) 中提出，是一种革命性的架构设计，它极大地缓解了梯度消失问题，使得训练数百甚至上千层的深度网络成为可能。

本文档将结合一个具体的 PyTorch 代码示例，详细阐述残差连接的实现、工作原理及其对梯度流的积极影响。

2. 残差连接的核心思想

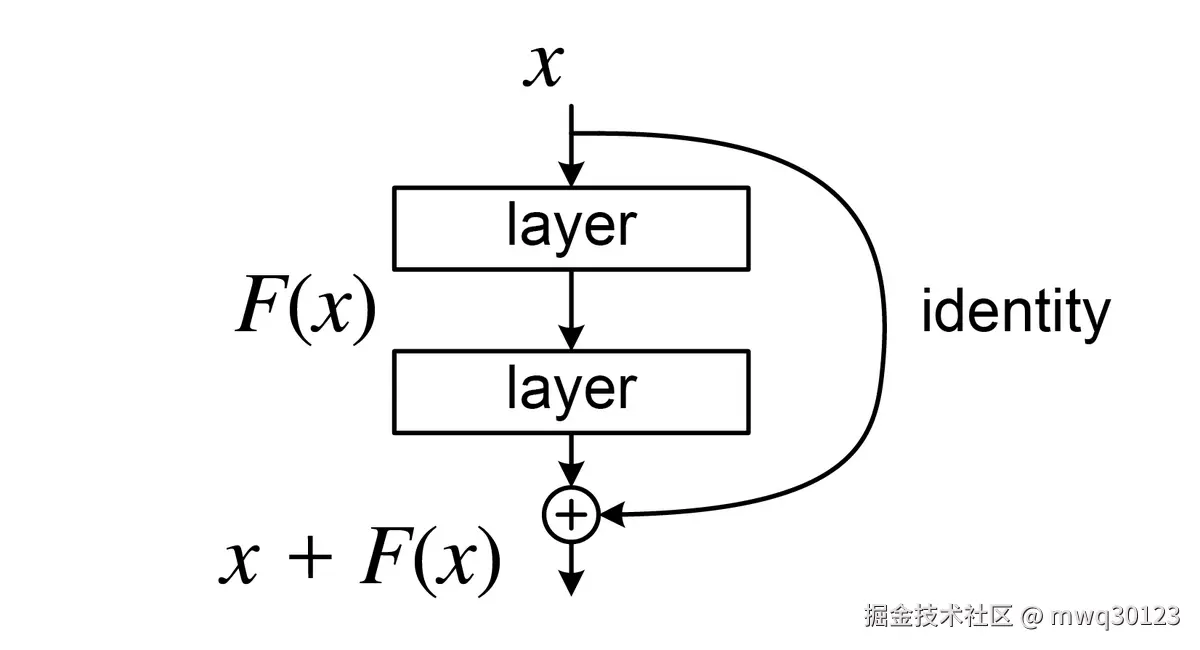
在传统的深度网络中，每一层的输出是其输入经过一系列变换（如线性变换和非线性激活）后的结果，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> H ( x ) H(x) </math>H(x)。而残差连接的核心思想是，不再让网络层直接学习目标函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> H ( x ) H(x) </math>H(x)，而是学习其残差 (residual) ，即 <math xmlns="http://www.w3.org/1998/Math/MathML"> F ( x ) = H ( x ) − x F(x) = H(x) - x </math>F(x)=H(x)−x。

这样，原始的目标函数就变成了 <math xmlns="http://www.w3.org/1998/Math/MathML"> H ( x ) = F ( x ) + x H(x) = F(x) + x </math>H(x)=F(x)+x。这个看似简单的加法操作，却有着深刻的意义：

恒等映射 (Identity Mapping) : 如果某个网络层对于当前任务不是必需的，模型可以通过将该层的权重学习为接近于零，使得 <math xmlns="http://www.w3.org/1998/Math/MathML"> F ( x ) ≈ 0 F(x) \approx 0 </math>F(x)≈0，从而让该层退化为一个恒等映射 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> H ( x ) = x H(x) = x </math>H(x)=x)。这使得添加新的网络层至少不会损害模型的性能，极大地简化了学习过程。
改善梯度流 : 在反向传播中，梯度可以通过这个"快捷连接"( <math xmlns="http://www.w3.org/1998/Math/MathML"> + x +x </math>+x)直接向前传递，而无需穿过多个非线性激活函数和权重层。这创建了一条梯度高速公路，有效缓解了梯度在深层传播中不断衰减的问题。

图示：一个残差块。输入 x 直接连接到层变换 F(x) 的输出，共同构成了最终的输出 H(x)。

3. 代码实现解析

我们通过分析提供的代码来理解残差连接在实践中是如何实现的。

3.1 网络架构 `ExampleDeepNeuralNetwork`

Python

python 复制代码

import torch
import torch.nn as nn

class ExampleDeepNeuralNetwork(nn.Module):
    def __init__(self, layer_sizes, use_shortcut):
        super().__init__()
        self.use_shortcut = use_shortcut
        # 定义多层网络，包含 5 层线性层和激活函数 ReLU
        self.layers = nn.ModuleList([
            nn.Sequential(nn.Linear(layer_sizes[0], layer_sizes[1]), nn.ReLU()),
            nn.Sequential(nn.Linear(layer_sizes[1], layer_sizes[2]), nn.ReLU()),
            nn.Sequential(nn.Linear(layer_sizes[2], layer_sizes[3]), nn.ReLU()),
            nn.Sequential(nn.Linear(layer_sizes[3], layer_sizes[4]), nn.ReLU()),
            nn.Sequential(nn.Linear(layer_sizes[4], layer_sizes[5]), nn.ReLU())
        ])
        # 定义一个五层的神经网络块，其中每层包含一个线性变换和一个激活函数 ReLU，
        # 类似 ResNet 的结构，支持添加残差连接。

    def forward(self, x):
        # 遍历每一层
        for layer in self.layers:
            # 当前层的输出
            layer_output = layer(x)
            # 检查是否可以应用残差连接
            if self.use_shortcut and x.shape == layer_output.shape:
                x = x + layer_output  # 如果输入和输出维度匹配，添加残差连接
            else:
                x = layer_output  # 否则直接输出当前层结果
        return x  # 返回最终结果

__init__ 函数:
- 通过 use_shortcut 布尔标志来控制是否启用残差连接，这使得我们能够轻松地对比有无残差连接时的效果。
- nn.ModuleList 用于存储多个网络层。
forward 函数 (核心) :
- 代码清晰地展示了残差连接的实现逻辑。在每次前向传播时，它都会检查 use_shortcut 是否为 True。
- 关键条件 : x.shape == layer_output.shape。残差连接要求进行相加操作的两个张量（即输入 x 和层输出 layer_output）必须具有完全相同的形状。在实际的 ResNet 中，如果维度不匹配，通常会通过一个额外的1x1卷积或线性层来调整输入的维度。
- 核心操作 : x = x + layer_output。这行代码就是残差连接的精髓，它将原始输入 x 直接加到经过变换后的 layer_output 上。

3.2 梯度观察函数 `print_gradients`

Python 复制代码

def print_gradients(model, x):
    output = model(x)
    target = torch.tensor([[0.]])
    loss = nn.MSELoss()(output, target)
    
    # 梯度清零（在实际训练中是必须的）
    model.zero_grad()
    
    # 反向传播，计算梯度
    loss.backward()

    # 打印每层权重的梯度均值
    print(f"--- 梯度分析 (use_shortcut={model.use_shortcut}) ---")
    for name, param in model.named_parameters():
        if 'weight' in name:
            print(f"{name} has gradient mean of {param.grad.abs().mean().item()}")

这个辅助函数通过计算损失并进行反向传播，来获取模型中每一层权重的梯度。通过比较 use_shortcut=True 和 use_shortcut=False 两种情况下各层梯度的均值，我们可以直观地观察到残差连接对梯度流的影响。

预期结果:
- use_shortcut=False (无残差连接) : 在深层网络中，靠近输入层的梯度（例如 layers.0...）会非常小，远小于靠近输出层的梯度，这正是梯度消失现象。
- use_shortcut=True (有残差连接) : 梯度能够更有效地从输出层传导回输入层。因此，我们预期所有层的梯度值会分布得更加均匀，即使是深层的网络，其浅层部分的梯度也不会过小，从而保证了整个网络的有效训练。

4. 实验与结论

通过运行上述代码，我们可以模拟一次训练迭代并观察梯度。

在没有残差链接的时候,梯度是这样的

python 复制代码

# 示例用法
layer_sizes = [3, 3, 3, 3, 3, 1]  

sample_input = torch.tensor([[1., 0., -1.]])

torch.manual_seed(123)
model_without_shortcut = ExampleDeepNeuralNetwork(
    layer_sizes, use_shortcut=False
)
print_gradients(model_without_shortcut, sample_input)
#一次一次输出梯度

python 复制代码

layers.0.0.weight has gradient mean of 0.0006875668186694384 
layers.1.0.weight has gradient mean of 0.0019083978841081262 
layers.2.0.weight has gradient mean of 0.0038205471355468035 
layers.3.0.weight has gradient mean of 0.0038610314950346947 
layers.4.0.weight has gradient mean of 0.02481495402753353

有残差的链接,梯度是这样的

python 复制代码

torch.manual_seed(123)
model_with_shortcut = ExampleDeepNeuralNetwork(
    layer_sizes, use_shortcut=True
)
print_gradients(model_with_shortcut, sample_input)
#引入了残差链接,发现梯度消失的缺点明显改善了

matlab 复制代码

layers.0.0.weight has gradient mean of 0.5557742714881897 
layers.1.0.weight has gradient mean of 0.09135335683822632 
layers.2.0.weight has gradient mean of 0.7913904190063477 
layers.3.0.weight has gradient mean of 0.21711303293704987 
layers.4.0.weight has gradient mean of 3.140749216079712

实验结果将清晰地表明，带有残差连接的模型，其梯度能够在网络中更顺畅地流动，浅层网络的梯度值得到了有效维持。

总结: 残差连接是一种简单而极其强大的架构创新。通过构建一条信息和梯度的"高速公路"，它成功地解决了深度神经网络中的梯度消失问题，使得构建和训练前所未有的深度模型成为现实，并已成为现代深度学习架构（如 Transformer）中不可或缺的基础组件。

Transformer : 深度神经网络中的残差连接 (Residual Connection)