在表征相似性分析中,我们关心的不是单个被试的数值,而是成对个体之间的相似性 :谁更像谁、这种相似性能否由行为或协变量解释,以及这种关系在统计上是否稳健。曼特尔检验(Mantel test)与其进阶版 MRQAP 提供了两条互补路径:前者用节点标签同步置换 做矩阵相关的显著性检验,后者把问题放进回归框架 ,在控制协变量的同时检验独立效应;而二元组混合线性模型(dyadic LME)则进一步用显式层级建模刻画"同一被试出现在多条边上"的依赖结构,提供可解释的效应量与置信区间。本文聚焦前两者的介绍。
- 曼特尔检验 (Mantel test)
曼特尔检验(Mantel test)用于评估同一对象集合上两张距离/相似度矩阵之间的关联:先将两矩阵上三角元素配对(可用 Pearson 或 Spearman)计算相关系数,以此作为统计量;随后通过同步重排其中一张矩阵的行列标签进行大量置换,形成零分布并据此给出显著性(p 值)。该方法不依赖独立同分布假设,适合生态学、遗传学、脑成像等基于"对象间距离"的研究;偏曼特尔检验,类似于偏相关,可在评估两矩阵关系时控制第个张矩阵。
在观影数据中做个体相似性表征(ISC-RSA)分析时,我们构建被试×被试的行为相似性矩阵和神经相似性矩阵,然后取两矩阵上三角计算(Pearson 或 Spearman)相关,并以节点标签同步置换 (对其中一张矩阵同时重排行列)获得零分布与 p 值,那么它在方法学上就是典型的曼特尔检验,而我们构建的相似性矩阵,在方法学上称为dyadic(成对关系/二元组)数据。它的核心特征是:观测单位是无序的主体对(矩阵对称、对角为空),同一被试出现在多条记录中导致强互依((i,j) 与 (i,k) 非独立)。

因为二元组(dyad)并非独立观测** :同一被试 i同时出现在 (i,j)、(i,k)... 多个对中,这些条目共享个体效应与噪声,彼此相关。若在置换检验中把上三角向量当作独立样本随意打乱,会破坏节点层面的相关结构与交换性假设 ,导致p 值偏小(I 类错误增加)或功效失真。正确做法是使用节点标签置换(joint relabeling) :对一张矩阵同时按同一置换重排行与列,从而保留"谁与谁成对"的依赖与矩阵的对称/空对角特性。**
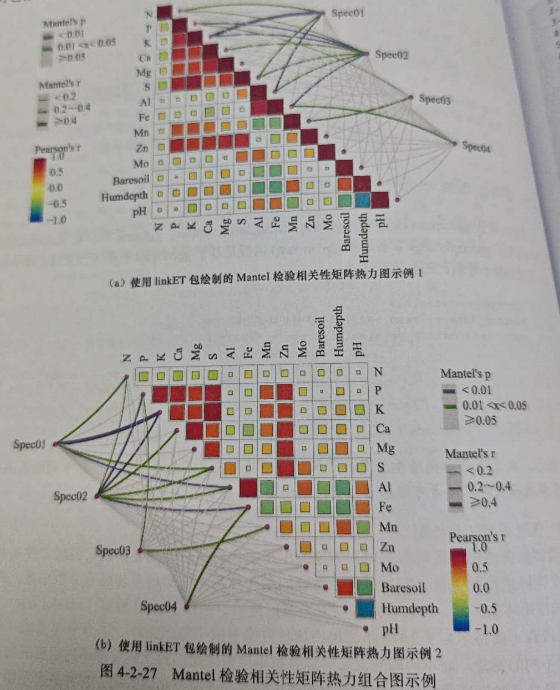
Mantel还会经常出现在这一类图中,皮尔逊相关展示变量之间的关系,Mantel相关计算矩阵之间的相关,在生态学、生信的分析中运用较多,神经影像中的运用场景并不是很多。
2. 多元回归二次指派程序(MRQAP)
Quadratic Assignment Procedure (QAP) 这个名字,最早是借用自经典的二次指派问题 (Quadratic Assignment Problem),比如你要给一组"设施"和一组"位置"做匹配(assignment),目标函数是一个关于指派矩阵的二次形式(quadratic form),所以叫 Quadratic Assignment。
后来,社会网络和心理测量领域的人在做"矩阵相关 / 矩阵回归 + 节点重排(permutation)"的时候,发现本质上也是在做一种"对节点标签做指派(重排),然后看某个二次统计量怎么变"的过程,就把这种基于节点置换来做推断的那一套方法 也叫成了 Quadratic Assignment Procedure 。
所以现在我们说的 QAP,更多是指 "一种在矩阵 / 网络数据上,用节点置换来做显著性检验的程序"。
在 Mantel 检验和 partial Mantel 检验中,我们通常只关注一对或少数几对矩阵之间的相关关系;然而在很多实际问题中,我们希望在回归框架(regression framework)下同时考虑多个关系矩阵的作用,并在控制协变量(covariates)的前提下,评估某一关系矩阵对目标关系的独立贡献。多元回归二次指派程序(Multiple Regression Quadratic Assignment Procedure, MRQAP)正是为此提出的:它将线性回归模型推广到成对/网络数据(dyadic or network data),同时利用节点置换来处理"同一节点出现在多个边上"所带来的非独立性(non-independence)。
在 MRQAP 中,已有多种基于节点置换的方案,包括最早的 naive QAP 回归、半偏法(semi-partialling, SP)、双半偏法(double semi-partialling, DSP)以及 Freedman--Lane 型残差置换(Freedman--Lane, FL)等。模拟研究表明,naive QAP 和 SP 在多协变量、共线情形下往往会高估Type1错误,而 DSP 与 FL 能更好地控制错误率,因此当前应用中通常推荐使用 DSP 或 FL。
1)naive QAP 回归
最早的 QAP 回归(有时直接就叫 QAP)就是:先把因变量矩阵 Y 和一组自变量矩阵 X1,...,Xp展平为 dyad 向量,用普通最小二乘回归估计回归系数,然后通过对节点标签做大量置换(同时重排 Y和所有 X的行列),每次重新回归、得到一组系数的置换分布,再据此计算 p 值。它的优点是概念清楚、实现简单,但在多协变量或自变量间高度相关时,型一错误往往偏高,现在多用于历史对比,而不是首选方法。
2)Semi-partialling(SP)
半偏法(semi-partialling, SP)是在 naive QAP 基础上的改进思路:对某个目标自变量矩阵 Xk,先将它对其他协变量矩阵做回归并取残差(即"剥离掉其他自变量后的独立部分"),然后用这个残差矩阵去预测 Y,并在置换时只对这个残差矩阵做节点置换,从而在控制协变量的前提下检验 Xk的独立效应。SP 相比 naive QAP 在多协变量情形下表现更好,但在某些设计下仍可能出现偏高的型一错误,因此后来又发展出 DSP 等更稳健的变体。
3)Double semi-partialling(DSP)
双半偏法(double semi-partialling, DSP)进一步在 SP 的基础上同时处理因变量和自变量:对每个目标自变量 Xk,不仅将 Xk 对其他协变量回归取残差,还将因变量矩阵 Y对其他协变量回归取残差,然后在置换中对这两个残差矩阵做节点置换,实质上是在"控制协变量后的 Y"与"控制协变量后的 Xk"之间做 Mantel 式检验。大量模拟表明,DSP 在控制Type1错误和保持检验效能之间有较好平衡,因此目前在 MRQAP 实际应用和软件默认设置中非常常见。
4)Freedman--Lane(FL)
Freedman--Lane(FL)方法原本是针对一般线性模型提出的一种残差置换检验方案,后来被引入 MRQAP 框架:先在完整模型(包含所有自变量)上拟合 Y=Xβ+e,得到残差矩阵 e;然后对残差矩阵做节点置换,构造新的 Y(perm)=Xβ^+e(perm),并在每次置换下重新拟合回归、形成系数的零分布。这样既保留了原模型结构,又通过残差置换捕捉到节点依赖带来的非独立性。模拟研究显示,FL 与 DSP 一样通常能较好地控制型一错误,因此在部分实现中作为与 DSP 并列的推荐选项。
目前比较常用的是DSP,在R中有多个工具包可以实现:
php
# validate_mrqap_R.R# Uses same CSVs written by MATLAB; runs MRQAP in Rset.seed(42)# PackagessuppressPackageStartupMessages({ library(asnipe) # mrqap.dsp (double semi-partialling) library(sna) # netlm (QAP-based network regression)})read_mat <- function(path) { as.matrix(read.csv(path, header = FALSE))}S_neural <- read_mat("S_neural.csv")S_behav <- read_mat("S_behav.csv")S_cov_sex <- read_mat("S_cov_sex.csv")S_cov_age <- read_mat("S_cov_age.csv")# Ensure symmetric with proper diag (should already be)diag(S_neural) <- 1diag(S_behav) <- 1diag(S_cov_sex) <- 1diag(S_cov_age) <- 1# ---------------- asnipe::mrqap.dsp (Double Semi-Partialling) ----------------# formula interface expects matrices on RHS as named objectsreps <- 2000fit_dsp <- mrqap.dsp(S_neural ~ S_behav + S_cov_sex + S_cov_age, reps = reps, directed = FALSE)cat("\nR asnipe::mrqap.dsp (DSP), reps =", reps, "\n")print(fit_dsp)# -------------- sna::netlm (QAP-based network regression baseline) -----------# netlm takes y and a list of X matrices; uses QAP permutations for p-valuesX_list <- list(S_behav, S_cov_sex, S_cov_age)fit_netlm <- netlm(S_neural, X_list, nullhyp = "qap", reps = reps, diag = FALSE, mode = "undirected")cat("\nR sna::netlm (QAP), reps =", reps, "\n")print(summary(fit_netlm))注:在netlm中设置qap即视为选择了DSP

3. 二元组混合线性模型(dyadic LME)
与 Mantel / MRQAP 通过置换来"校正"二元组非独立性不同,二元组混合线性模型(dyadic LME)采用显式建模(explicit modeling)的方式,将共享同一节点(individual)的二元组视作一种交叉随机效应结构(crossed random effects)。
MRQAP 很适合做相关性+协变量控制** 并给出稳健的置换 p 值,但它是"检验导向"的;dyadic LME 存在的意义在于提供基于生成模型的估计与分解 :它能在二元组依赖下给出可解释的效应量与置信区间 (不仅是 p ),显式建模层级/重复测量 (被试 i 、被试 j 、ROI 的随机截距与随机斜率),还具备处理不平衡数据与缺失 、可拓展性高等优点。**
在实际实现中,dyadic LME 可以通过混合效应建模工具完成(例如 R 中的 lme4::lmer 或 nlme),用到再试。
推荐阅读