1 介绍
本文会介绍二叉树三种遍历:
- 前序遍历
- 中序遍历
- 后序遍历
的两种常见方法:
- 递归法
- 迭代法
以及一种进阶的遍历方法:莫里斯(Morris)遍历。
2 前序遍历
2.1 原题

2.2 递归法
递归是一种最常见并且最直接的遍历方法,直接就是按照前序遍历的定义去实现:
- 访问根节点
- 再遍历左子树
- 最后右子树
代码实现如下:
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode *root) {
vector<int> res;
auto dfs = [&](this auto &&dfs, TreeNode *node) -> void {
// 如果当前节点为空直接返回
if (!node) {
return;
}
// 遍历当前根节点
res.push_back(node->val);
// 遍历左
dfs(node->left);
// 遍历右
dfs(node->right);
};
dfs(root);
return res;
}
};2.3 迭代法
迭代法的写法有很多种,这里介绍一种三种遍历方式写法都比较类似以及好记忆的。
首先需要明确的是,迭代法的本质就是模拟栈,因为递归的本质就是栈。
所以需要一个变量存储当前遍历的节点,最合适的就是数据结构栈。
在具体实现上,每个节点采取入栈两次(出栈也会有两次)的原则:
- 第一次入栈:相当于占位符,没有操作
- 第一次出栈:决定下一个节点的遍历顺序
- 第二次入栈:修改标志位
- 第二次出栈:存储结果
这种做法的本质上就是第一次的时候控制遍历顺序,实现前/中/后序遍历,然后第二次遍历的时候存储结果。
代码实现如下:
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode *root) {
// 栈
// 第一个元素是节点,第二个表示是否第一次入栈,第一次入栈就是0,否则是1
stack<pair<TreeNode *, int> > s;
// 判空处理
if (root) {
// 第一次入栈就是0
s.emplace(root, 0);
}
// 存储结果
vector<int> res;
// 遍历栈直到栈为空
while (!s.empty()) {
// 取栈顶
auto [node,val] = s.top();
// 出栈
s.pop();
// 如果node这个节点是第一次出栈
if (val == 0) {
// 因为前序遍历是根左右
// 换成入栈的话,右左根
if (node->right) {
// 入栈右节点
s.emplace(node->right, 0);
}
if (node->left) {
// 接着入栈左节点
s.emplace(node->left, 0);
}
// 最后入栈当前根节点
// val设置为1,表示第二次入栈了
s.emplace(node, 1);
} else {
// 第二次出栈,存储结果
res.push_back(node->val);
}
}
return res;
}
};2.4 莫里斯遍历
莫里斯遍历是一种用于二叉树遍历的巧妙算法,可以在O(1)空间下完成二叉树遍历。
实现上是通过利用二叉树叶子节点的空指针,使其指向前驱或者后继节点,实现空间优化,遍历完成之后会恢复原来的结构。
莫里斯中最重要的是一个前驱的概念,一个节点的前驱是左孩子中最右边的节点,这点对于前中后序遍历都是一样的。
而叶子节点的空指针,就是用来指向前驱节点的,这样就模拟了递归中归的部分。
代码实现(带详细注释):
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode *root) {
// 存储结果
vector<int> res;
// 当前的节点位置
auto cur = root;
// 判空
while (cur) {
// 如果左子树不为空
if (cur->left) {
auto pre = cur->left;
// 找到这个左孩子最右边的节点
while (pre->right && pre->right != cur) {
pre = pre->right;
}
// 如果左孩子最右边的节点不为空,表明之前已经设置过前驱了,并且前驱就是cur
// 所以前面的while除了判空之外,还要判pre->right != cur,不然就会死循环
if (pre->right) {
// 需要将叶子节点的右孩子复原,也就是置为空,因为原本就是空的
pre->right = nullptr;
// 然后访问当前节点的右子树,因为左子树遍历完了
cur = cur->right;
} else {
// 如果为空,将左孩子最右边的节点指向前驱,也就是cur
pre->right = cur;
// 存储结果,这个和中序遍历不同,一会可以看到
res.push_back(cur->val);
// 遍历左子树,右子树后续遍历
cur = cur->left;
}
} else {
// 存储结果
res.push_back(cur->val);
// 遍历右子树,因为左孩子为空,当前节点也遍历了,只能遍历右子树
cur = cur->right;
}
}
return res;
}
};2.5 Java版本
2.5.1 递归法
java
import java.util.*;
public class Solution {
private final List<Integer> res = new ArrayList<>();
private void dfs(TreeNode node) {
if (node == null) {
return;
}
res.add(node.val);
dfs(node.left);
dfs(node.right);
}
public List<Integer> preorderTraversal(TreeNode root) {
dfs(root);
return res;
}
}2.5.2 迭代法
java
import java.util.*;
public class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
LinkedList<TreeNode> nodeStack = new LinkedList<>();
LinkedList<Integer> valStack = new LinkedList<>();
if (root != null) {
nodeStack.push(root);
valStack.push(0);
}
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
Integer val = valStack.pop();
if (val == 0) {
if (node.right != null) {
nodeStack.push(node.right);
valStack.push(0);
}
if (node.left != null) {
nodeStack.push(node.left);
valStack.push(0);
}
nodeStack.push(node);
valStack.push(1);
} else {
res.add(node.val);
}
}
return res;
}
}2.5.3 莫里斯
java
import java.util.*;
public class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode cur = root;
while (cur != null) {
if (cur.left != null) {
TreeNode pre = cur.left;
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
if (pre.right != null) {
pre.right = null;
cur = cur.right;
} else {
pre.right = cur;
res.add(cur.val);
cur = cur.left;
}
} else {
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
}2.6 Go版本
2.6.1 递归法
go
func preorderTraversal(root *TreeNode) []int {
res := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
res = append(res, node.Val)
dfs(node.Left)
dfs(node.Right)
}
dfs(root)
return res
}2.6.2 迭代法
go
func preorderTraversal(root *TreeNode) []int {
res, nodeStack, valStack := make([]int, 0), make([]*TreeNode, 0), make([]int, 0)
if root != nil {
nodeStack = append(nodeStack, root)
valStack = append(valStack, 0)
}
for len(nodeStack) > 0 {
node, val := nodeStack[len(nodeStack)-1], valStack[len(valStack)-1]
nodeStack, valStack = nodeStack[:len(nodeStack)-1], valStack[:len(valStack)-1]
if val == 0 {
if node.Right != nil {
nodeStack = append(nodeStack, node.Right)
valStack = append(valStack, 0)
}
if node.Left != nil {
nodeStack = append(nodeStack, node.Left)
valStack = append(valStack, 0)
}
nodeStack = append(nodeStack, node)
valStack = append(valStack, 1)
} else {
res = append(res, node.Val)
}
}
return res
}2.6.3 莫里斯
go
func preorderTraversal(root *TreeNode) []int {
res, cur := make([]int, 0), root
for cur != nil {
if cur.Left != nil {
pre := cur.Left
for pre.Right != nil && pre.Right != cur {
pre = pre.Right
}
if pre.Right != nil {
pre.Right = nil
cur = cur.Right
} else {
pre.Right = cur
res = append(res, cur.Val)
cur = cur.Left
}
} else {
res = append(res, cur.Val)
cur = cur.Right
}
}
return res
}3 中序遍历
3.1 原题

3.2 递归法
直接根据定义去实现:
- 先遍历左子树
- 访问根节点
- 再遍历右子树
cpp
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
auto dfs = [&](this auto &&dfs,TreeNode*node) -> void {
// 判空
if (!node) {
return;
}
// 左子树
dfs(node->left);
// 访问根节点
res.push_back(node->val);
// 右子树
dfs(node->right);
};
dfs(root);
return res;
}
};3.3 迭代法
迭代法的详细描述见前面的前序遍历。
这里直接放上代码:
cpp
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
// 栈
// 第一个元素是节点,第二个表示是否第一次入栈,第一次入栈就是0,否则是1
stack<pair<TreeNode *, int> > s;
// 判空处理
if (root) {
// 第一次入栈就是0
s.emplace(root, 0);
}
// 存储结果
vector<int> res;
// 遍历栈直到栈为空
while (!s.empty()) {
// 取栈顶
auto [node,val] = s.top();
// 出栈
s.pop();
// 如果node这个节点是第一次出栈
if (val == 0) {
// 因为中序遍历是左根右
// 换成入栈的话,右根左
if (node->right) {
// 入栈右节点
s.emplace(node->right, 0);
}
// 接着入栈当前根节点
// val设置为1,表示第二次入栈了
s.emplace(node, 1);
if (node->left) {
// 最后入栈左节点
s.emplace(node->left, 0);
}
} else {
// 第二次出栈,存储结果
res.push_back(node->val);
}
}
return res;
}
};和前序的区别仅仅在于下面这段代码:
cpp
if (node->right) {
s.emplace(node->right, 0);
}
// 中序是放在这里
// s.emplace(node, 1);
if (node->left) {
s.emplace(node->left, 0);
}
// 前序是放在这里
// s.emplace(node, 1);3.4 莫里斯遍历
莫里斯的原理见前序遍历,这里说一下区别。
区别就在于中序遍历是在当前节点cur的左孩子最右边节点设置为空的时候,存储结果,而前序遍历是在设置前驱的时候存储结果。
代码如下:
cpp
class Solution {
public:
vector<int> inorderTraversal(TreeNode *root) {
// 存储结果
vector<int> res;
// 当前的节点位置
auto cur = root;
// 判空
while (cur) {
// 如果左子树不为空
if (cur->left) {
auto pre = cur->left;
// 找到这个左孩子最右边的节点
while (pre->right && pre->right != cur) {
pre = pre->right;
}
// 如果左孩子最右边的节点不为空,表明之前已经设置过前驱了,并且前驱就是cur
// 所以前面的while除了判空之外,还要判pre->right != cur,不然就会死循环
if (pre->right) {
// 需要将叶子节点的右孩子复原,也就是置为空,因为原本就是空的
pre->right = nullptr;
// 中序遍历在这里存储结果
res.push_back(cur->val);
// 然后访问当前节点的右子树,因为左子树遍历完了
cur = cur->right;
} else {
// 如果为空,将左孩子最右边的节点指向前驱,也就是cur
pre->right = cur;
// 遍历左子树,右子树后续遍历
cur = cur->left;
}
} else {
// 存储结果
res.push_back(cur->val);
// 遍历右子树,因为左孩子为空,当前节点也遍历了,只能遍历右子树
cur = cur->right;
}
}
return res;
}
};产生这样的区别是因为,中序遍历是先遍历完左子树再访问根节点的。
解释在下面这段代码中:
cpp
if (pre->right) {
// 进入到这个if,表明cur的左子树已经访问完毕了
// 因此这里保存cur的值,也就是当前根的值
pre->right = nullptr;
res.push_back(cur->val);
// 接着访问右子树
cur = cur->right;
} else {
pre->right = cur;
cur = cur->left;
}3.5 Java版本
3.5.1 递归法
java
import java.util.*;
public class Solution {
private final List<Integer> res = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
dfs(root);
return res;
}
private void dfs(TreeNode node) {
if (node == null) {
return;
}
dfs(node.left);
res.add(node.val);
dfs(node.right);
}
}3.5.2 迭代法
java
import java.util.*;
public class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
LinkedList<TreeNode> nodeStack = new LinkedList<>();
LinkedList<Integer> valStack = new LinkedList<>();
if (root != null) {
nodeStack.push(root);
valStack.push(0);
}
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
Integer val = valStack.pop();
if (val == 0) {
if (node.right != null) {
nodeStack.push(node.right);
valStack.push(0);
}
nodeStack.push(node);
valStack.push(1);
if (node.left != null) {
nodeStack.push(node.left);
valStack.push(0);
}
} else {
res.add(node.val);
}
}
return res;
}
}3.5.3 莫里斯
java
import java.util.*;
public class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode cur = root;
while (cur != null) {
if (cur.left != null) {
TreeNode pre = cur.left;
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
if (pre.right != null) {
pre.right = null;
res.add(cur.val);
cur = cur.right;
} else {
pre.right = cur;
cur = cur.left;
}
} else {
res.add(cur.val);
cur = cur.right;
}
}
return res;
}
}3.6 Go版本
3.6.1 递归法
go
func inorderTraversal(root *TreeNode) []int {
res := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
res = append(res, node.Val)
dfs(node.Right)
}
dfs(root)
return res
}3.6.2 迭代法
go
func inorderTraversal(root *TreeNode) []int {
res, nodeStack, valStack := make([]int, 0), make([]*TreeNode, 0), make([]int, 0)
if root != nil {
nodeStack = append(nodeStack, root)
valStack = append(valStack, 0)
}
for len(nodeStack) > 0 {
node, val := nodeStack[len(nodeStack)-1], valStack[len(valStack)-1]
nodeStack, valStack = nodeStack[:len(nodeStack)-1], valStack[:len(valStack)-1]
if val == 0 {
if node.Right != nil {
nodeStack = append(nodeStack, node.Right)
valStack = append(valStack, 0)
}
nodeStack = append(nodeStack, node)
valStack = append(valStack, 1)
if node.Left != nil {
nodeStack = append(nodeStack, node.Left)
valStack = append(valStack, 0)
}
} else {
res = append(res, node.Val)
}
}
return res
}3.6.3 莫里斯
go
func inorderTraversal(root *TreeNode) []int {
res, cur := make([]int, 0), root
for cur != nil {
if cur.Left != nil {
pre := cur.Left
for pre.Right != nil && pre.Right != cur {
pre = pre.Right
}
if pre.Right != nil {
pre.Right = nil
res = append(res, cur.Val)
cur = cur.Right
} else {
pre.Right = cur
cur = cur.Left
}
} else {
res = append(res, cur.Val)
cur = cur.Right
}
}
return res
}4 后序遍历
4.1 原题
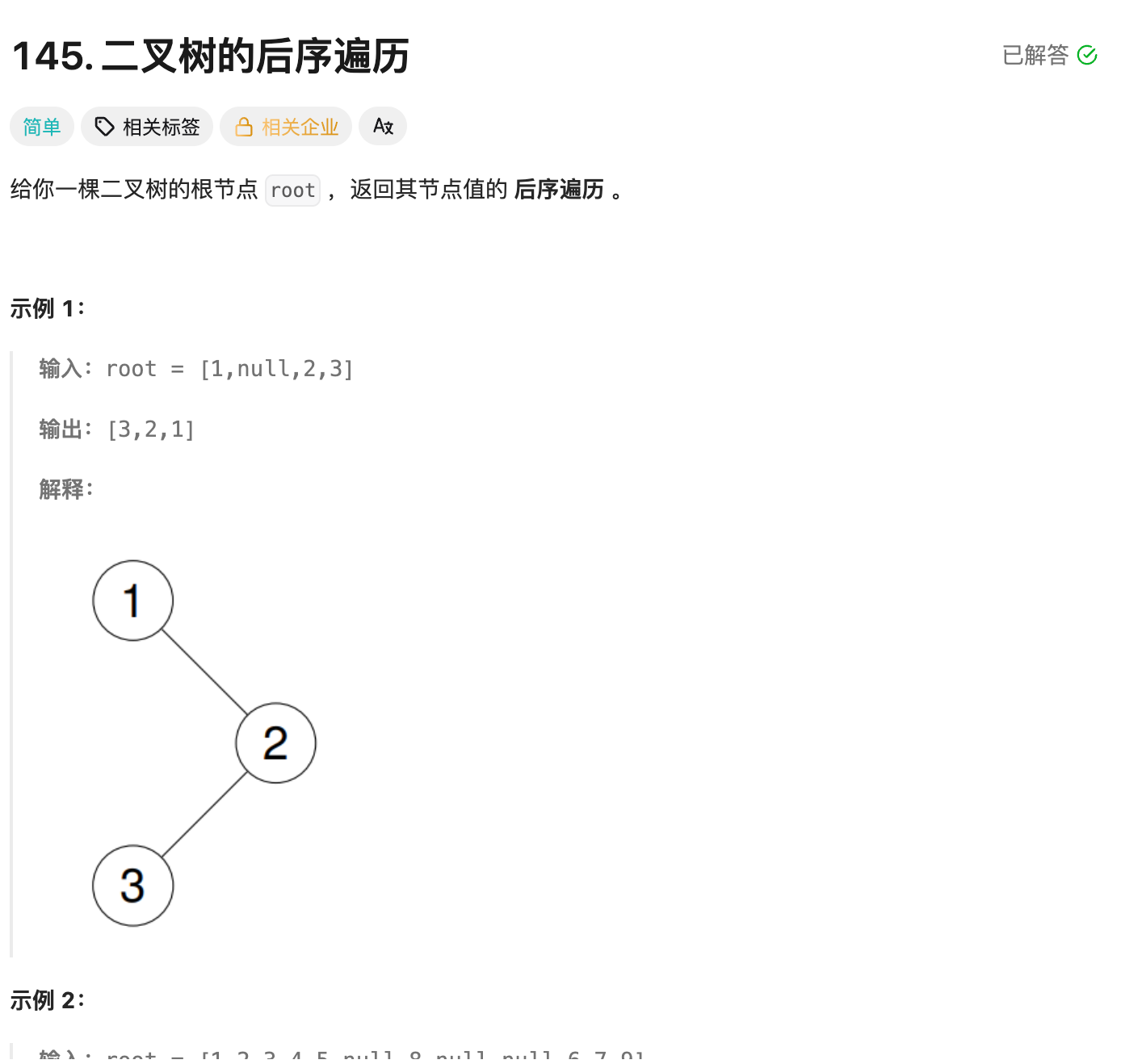
4.2 递归法
直接根据定义实现:
- 先遍历左子树
- 再遍历右子树
- 最后访问根节点
cpp
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
auto dfs = [&](this auto &&dfs, TreeNode *node) -> void {
// 判空
if (!node) {
return;
}
// 左子树
dfs(node->left);
// 右子树
dfs(node->right);
// 访问根节点
res.push_back(node->val);
};
dfs(root);
return res;
}
};4.3 迭代法
迭代法的详细描述见前面的前序遍历。
这里直接放上代码:
cpp
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
// 栈
// 第一个元素是节点,第二个表示是否第一次入栈,第一次入栈就是0,否则是1
stack<pair<TreeNode *, int> > s;
// 判空处理
if (root) {
// 第一次入栈就是0
s.emplace(root, 0);
}
// 存储结果
vector<int> res;
// 遍历栈直到栈为空
while (!s.empty()) {
// 取栈顶
auto [node,val] = s.top();
// 出栈
s.pop();
// 如果node这个节点是第一次出栈
if (val == 0) {
// 因为后序遍历是左右根
// 换成入栈的话,顺序就是根右左
// val设置为1,表示第二次入栈了
s.emplace(node, 1);
if (node->right) {
// 接着入栈右节点
s.emplace(node->right, 0);
}
if (node->left) {
// 最后入栈左节点
s.emplace(node->left, 0);
}
} else {
// 第二次出栈,存储结果
res.push_back(node->val);
}
}
return res;
}
};和中序的区别仅仅在于下面这段代码:
cpp
// 后序是放在这里
// s.emplace(node, 1);
if (node->right) {
s.emplace(node->right, 0);
}
// 中序是放在这里
// s.emplace(node, 1);
if (node->left) {
s.emplace(node->left, 0);
}4.4 莫里斯遍历
用莫里斯来实现后序遍历和前面前序和中序的思路不同,前面已经介绍了,莫里斯的特点:
- 天然适合处理"进入左子树"和回来的时机(也就是代码中的
if(pre->right){}部分) - 但不能告诉你"右子树是否处理完成"
而后序遍历是需要先遍历左子树和右子树,最后才处理根节点。
所以需要一种办法,处理完成左子树后,优先处理右子树,这种方法就是反转这条右链(右链的图示可以见6.2小节)。
反转的话需要用到反转链表的技巧,这里由于篇幅限制不进行展开,反转之后,需要对树进行还原,因此下面的print_reverse函数,是先反转一次,打印右链,然后再反转一次,进行复原操作。
代码实现如下,带详细注释:
cpp
class Solution {
public:
vector<int> postorderTraversal(TreeNode *root) {
// 存储结果
vector<int> res;
// 反转链表,见LeetCode原题,这里不解释了
auto reverse_list = [](TreeNode *node) -> TreeNode * {
const auto dummy = new TreeNode();
while (node) {
const auto next = node->right;
node->right = dummy->right;
dummy->right = node;
node = next;
}
const auto reverse_res = dummy->right;
delete dummy;
return reverse_res;
};
// 逆向打印
auto print_reverse = [&](TreeNode *node) {
// 反转node
const auto l = reverse_list(node);
// 遍历整条链(right)
for (auto temp = l; temp; temp = temp->right) {
res.push_back(temp->val);
}
// 复原
reverse_list(l);
};
// 当前的节点位置
auto cur = root;
// 判空
while (cur) {
// 如果左子树不为空
if (cur->left) {
auto pre = cur->left;
// 找到这个左子树最右边的节点
while (pre->right && pre->right != cur) {
pre = pre->right;
}
// 如果左子树最右边的节点不为空,表明之前已经设置过前驱了,并且前驱就是cur
// 所以前面的while除了判空之外,还要判pre->right != cur,不然就会死循环
if (pre->right) {
// 需要将叶子节点的右孩子复原,也就是置为空,因为原本就是空的
pre->right = nullptr;
// 逆向打印结果,这里是left,表示当前节点的左子树
// 因为print_reverse()是处理右子树的,因此是逆向打印当前节点的左子树的右链
// 这里的右链也包含cur自己,也就是根,因此不需要额外的res.push_back(cur->val);去存储根的结果
print_reverse(cur->left);
// 然后访问当前节点的右子树,因为左子树遍历完了
cur = cur->right;
} else {
// 如果为空,将左子树最右边的节点指向前驱,也就是cur
pre->right = cur;
// 遍历左子树,右子树后续遍历
cur = cur->left;
}
} else {
// 遍历右子树,因为左子树为空
cur = cur->right;
}
}
// 逆向打印一次root
print_reverse(root);
return res;
}
};和前序以及中序不同的是,不需要额外的res.push_back(cur->val)记录结果,而是直接使用print_reverse()去直接结果。
遍历完成后,最后还需要一次print_reverse(root)。(原因可以见6.2小节)
4.5 Java版本
4.5.1 递归法
java
import java.util.*;
public class Solution {
private final List<Integer> res = new ArrayList<>();
public List<Integer> postorderTraversal(TreeNode root) {
dfs(root);
return res;
}
private void dfs(TreeNode node) {
if (node == null) {
return;
}
dfs(node.left);
dfs(node.right);
res.add(node.val);
}
}4.5.2 迭代法
java
import java.util.*;
public class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
LinkedList<TreeNode> nodeStack = new LinkedList<>();
LinkedList<Integer> valStack = new LinkedList<>();
if (root != null) {
nodeStack.push(root);
valStack.push(0);
}
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
Integer val = valStack.pop();
if (val == 0) {
nodeStack.push(node);
valStack.push(1);
if (node.right != null) {
nodeStack.push(node.right);
valStack.push(0);
}
if (node.left != null) {
nodeStack.push(node.left);
valStack.push(0);
}
} else {
res.add(node.val);
}
}
return res;
}
}4.5.3 莫里斯
java
import java.util.*;
public class Solution {
private final List<Integer> res = new ArrayList<>();
private TreeNode reverse(TreeNode node) {
TreeNode dummy = new TreeNode();
while (node != null) {
TreeNode next = node.right;
node.right = dummy.right;
dummy.right = node;
node = next;
}
return dummy.right;
}
private void printReverse(TreeNode node) {
TreeNode l = reverse(node);
for (TreeNode temp = l; temp != null; temp = temp.right) {
res.add(temp.val);
}
reverse(l);
}
public List<Integer> postorderTraversal(TreeNode root) {
TreeNode cur = root;
while (cur != null) {
if (cur.left != null) {
TreeNode pre = cur.left;
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
if (pre.right != null) {
pre.right = null;
printReverse(cur.left);
cur = cur.right;
} else {
pre.right = cur;
cur = cur.left;
}
} else {
cur = cur.right;
}
}
printReverse(root);
return res;
}
}4.6 Go版本
4.6.1 递归法
go
func postorderTraversal(root *TreeNode) []int {
res := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
dfs(node.Right)
res = append(res, node.Val)
}
dfs(root)
return res
}4.6.2 迭代法
go
func postorderTraversal(root *TreeNode) []int {
res, nodeStack, valStack := make([]int, 0), make([]*TreeNode, 0), make([]int, 0)
if root != nil {
nodeStack = append(nodeStack, root)
valStack = append(valStack, 0)
}
for len(nodeStack) > 0 {
node, val := nodeStack[len(nodeStack)-1], valStack[len(valStack)-1]
nodeStack, valStack = nodeStack[:len(nodeStack)-1], valStack[:len(valStack)-1]
if val == 0 {
nodeStack = append(nodeStack, node)
valStack = append(valStack, 1)
if node.Right != nil {
nodeStack = append(nodeStack, node.Right)
valStack = append(valStack, 0)
}
if node.Left != nil {
nodeStack = append(nodeStack, node.Left)
valStack = append(valStack, 0)
}
} else {
res = append(res, node.Val)
}
}
return res
}4.6.3 莫里斯
go
func postorderTraversal(root *TreeNode) []int {
res, cur := make([]int, 0), root
reverseList := func(node *TreeNode) *TreeNode {
dummy := &TreeNode{Val: 0}
for node != nil {
next := node.Right
node.Right = dummy.Right
dummy.Right = node
node = next
}
return dummy.Right
}
printReverse := func(node *TreeNode) {
l := reverseList(node)
for temp := l; temp != nil; temp = temp.Right {
res = append(res, temp.Val)
}
reverseList(l)
}
for cur != nil {
if cur.Left != nil {
pre := cur.Left
for pre.Right != nil && pre.Right != cur {
pre = pre.Right
}
if pre.Right != nil {
pre.Right = nil
printReverse(cur.Left)
cur = cur.Right
} else {
pre.Right = cur
cur = cur.Left
}
} else {
cur = cur.Right
}
}
printReverse(root)
return res
}5 关于迭代法
可以看到,三种迭代法的写法非常类似:
cpp
// 后序是放在这里
// s.emplace(node, 1);
if (node->right) {
s.emplace(node->right, 0);
}
// 中序是放在这里
// s.emplace(node, 1);
if (node->left) {
s.emplace(node->left, 0);
}
// 前序是放这里
// s.emplace(node, 1);区别仅仅在于
cpp
s.emplace(node, 1);放的位置不同。
放的位置不同正好也对应着入栈的顺序,因为迭代法的本质就是用数据结构stack来模拟函数调用的栈:
- 对于前序:遍历顺序要求根左右,那么入栈顺序就是右左根
- 对于中序:遍历顺序要求左根右,那么入栈顺序就是右根左
- 对于后序:遍历顺序要求左右根,那么入栈顺序就是根右左
笔者之前看过很多迭代的写法,在前中后遍历上非常不一致,很多特殊的判断(例如各种if等),而这种写法在三种方式的遍历下都比较一致,笔者比较推荐这种写法。
6 关于莫里斯
6.1 莫里斯的本质是什么
莫里斯的本质就是用前驱来模拟递归中的归。
对于普通的递归法来说,找到前驱是很容易的,一直return就可以了,但是对于没有栈的迭代来说,这需要使用额外的手段,这个手段就是前驱节点。
莫里斯遍历非常巧妙地利用了叶子节点的空节点,使其指向前驱,这样就能模拟出return的效果。
6.2 为什么后序遍历需要逆向打印一次root
见原题示例2:
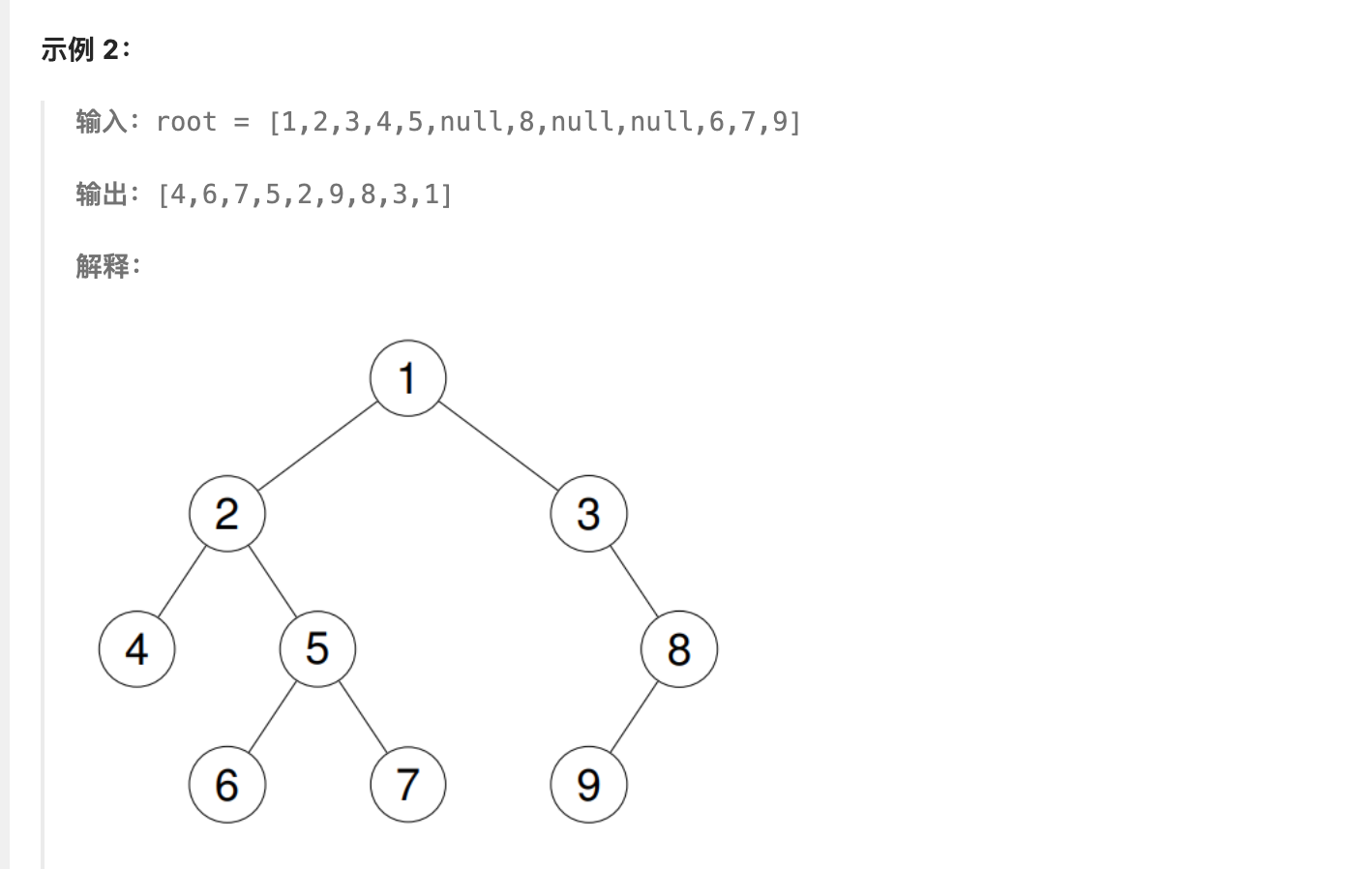
如果没有加
cpp
print_reverse(root);输出就会变成:

可以看到刚好少了右链的位置。
而print_reverse正好是解决这个问题的,逆序右链并打印,然后还原。
7 总结
本文介绍了二叉树三种遍历的三种实现方法:
- 递归法:最常见的方法
- 迭代法:用数据结构
stack模拟函数调用栈 - 莫里斯遍历:用前驱节点模拟函数调用栈
这三种方法实现起来最难的是莫里斯,但是同时莫里斯也是唯一一个能做到O(1)空间去遍历二叉树的做法。
附录上有原题链接。