数据结构（5）

树和森林

一、树转化为二叉树

[1. 基本步骤](#1. 基本步骤)

[2. 详细介绍](#2. 详细介绍)

（1）核心转化法则：左孩子右兄弟

（2）具体转化步骤（以一棵普通树为例）

[3. 转化后的二叉树特性](#3. 转化后的二叉树特性)

二、反向还原（二叉树→普通树）

三、森林转为二叉树

[1. 基本方法描述](#1. 基本方法描述)

[2. 详细介绍](#2. 详细介绍)

（1）核心转化步骤

[（2）示例说明（以包含 2 棵树的森林为例）](#（2）示例说明（以包含 2 棵树的森林为例）)

[3. 转化后的二叉树特性](#3. 转化后的二叉树特性)

树和森林

一、树转化为二叉树

1. 基本步骤

（1）加线：将树中同一结点的兄弟相连

（2）抹线：保留结点的最左孩子连线，删除其他孩子连线

（3）旋转：将同一根的孩子的连线绕左孩子（排在这个孩子左边的孩子）旋转45°

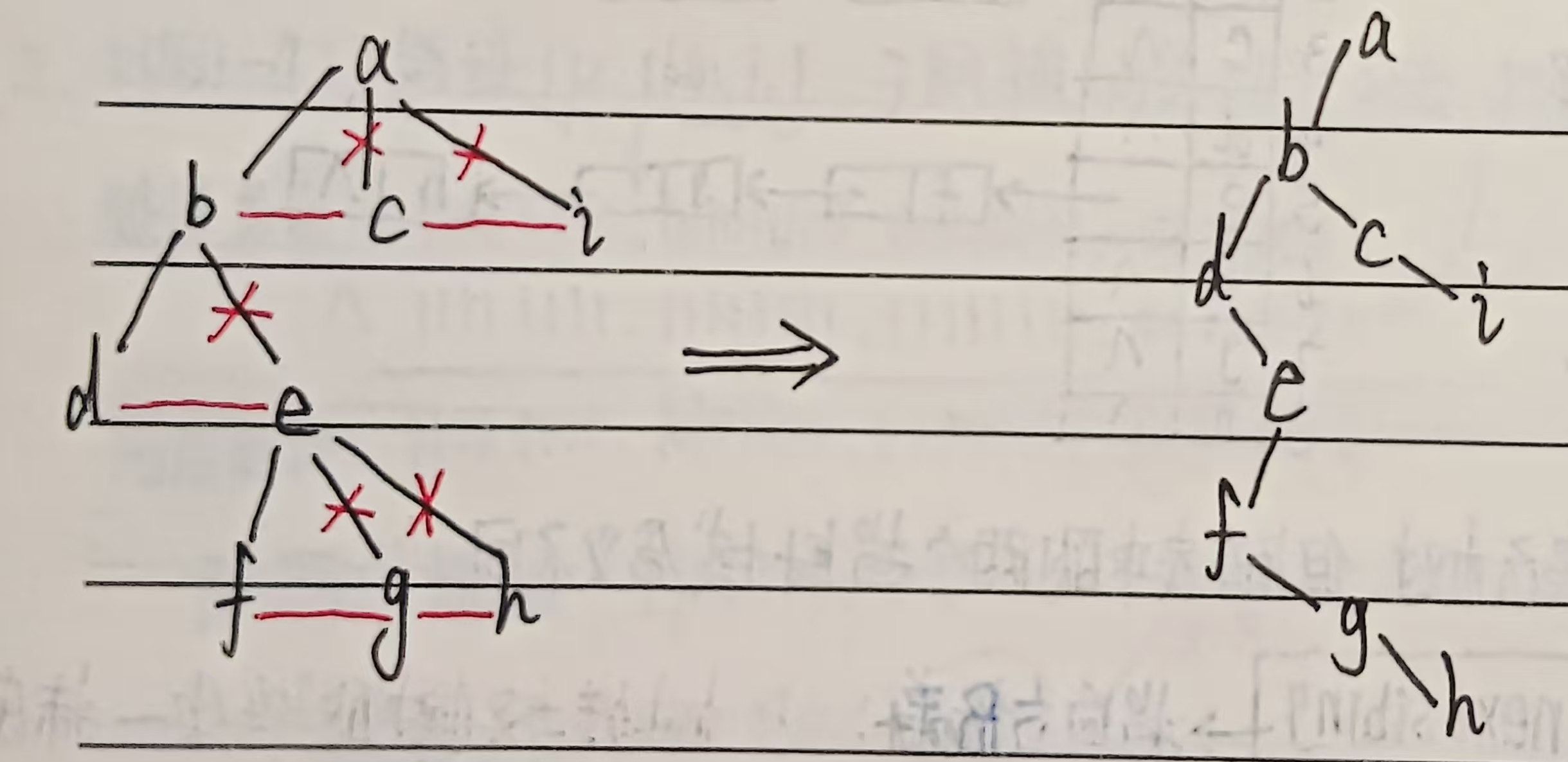
2. 详细介绍

树（普通树，非二叉树）转化为二叉树的核心是利用二叉树的左、右指针分别表示 "孩子" 和 "兄弟" 关系，通过 "左孩子右兄弟" 法则，将普通树的多叉结构（一个节点可有多孩子）转化为二叉树的二叉结构，且转化后能唯一还原原树。

（1）核心转化法则：左孩子右兄弟

普通树中，一个节点可能有多个直接孩子（如节点 A 有孩子 B、C、D），转化时遵循以下规则：

① 处理孩子关系：将节点的第一个孩子作为二叉树中的左孩子（左指针指向第一个孩子）。

② 处理兄弟关系：将节点的其他孩子（第二个及以后的孩子）依次作为前一个孩子的右孩子（右指针指向兄弟节点）。

③ 递归处理：对每个节点的所有孩子，重复步骤 ① 和 ②，直至整棵树转化完成。

（2）具体转化步骤（以一棵普通树为例）

假设普通树结构如下（节点 A 为根，A 的孩子为 B、C、D；B 的孩子为 E、F；D 的孩子为 G）：

复制代码

        A
      / | \
     B  C  D
    / \     \
   E   F     G

转化为二叉树的步骤：

① 处理根节点 A：

a. A 的第一个孩子是 B，将 A 的左指针指向 B（A 的左孩子 = B）。

b. A 的其他孩子是 C、D，需作为 B 的兄弟：将 B 的右指针指向 C（B 的右兄弟 = C），再将 C 的右指针指向 D（C 的右兄弟 = D）。

② 处理节点 B：

a. B 的第一个孩子是 E，将 B 的左指针指向 E（B 的左孩子 = E）。

b. B 的其他孩子是 F，将 E 的右指针指向 F（E 的右兄弟 = F）。

③ 处理节点 D：

c. D 的第一个孩子是 G，将 D 的左指针指向 G（D 的左孩子 = G）。

d. D 无其他孩子，无需处理右兄弟。

④ 其他节点（C、E、F、G）：无孩子或已处理，转化结束。

最终转化后的二叉树结构：

复制代码

3. 转化后的二叉树特性

① 结构唯一性：每棵普通树对应唯一的二叉树，且可通过反向规则（左孩子仍为孩子，右孩子视为兄弟）还原原普通树。

② 根节点特性：转化后的二叉树，根节点无右孩子（因为普通树的根节点没有兄弟）。

③ 关系映射：

a. 二叉树的 "左指针" 仅表示原树的 "孩子" 关系。

b. 二叉树的 "右指针" 仅表示原树的 "兄弟" 关系，与二叉树本身的 "右孩子" 概念无关。

二、反向还原（二叉树→普通树）

若需从转化后的二叉树还原回普通树，遵循以下规则：

（1）节点的左孩子仍为原树中的 "第一个孩子"。

（2）节点的右孩子（及右孩子的右孩子）均为原树中该节点的 "兄弟"，需将这些右孩子依次作为原节点的直接孩子。

（3）递归处理每个节点，直至还原所有层级的孩子关系。

转化的意义

将普通树转化为二叉树，核心价值是统一数据结构的操作逻辑：

（1）普通树的多叉结构会导致操作（如遍历、插入、删除）实现复杂（需处理数量不确定的孩子）。

（2）转化为二叉树后，可直接复用二叉树的成熟算法（如前序 / 中序 / 后序遍历、递归操作），降低实现难度，提高效率。

三、森林转为二叉树

1. 基本方法描述

（1）方法一

各森林中各树先各自转为二叉树；依次连到前一个二叉树的右子树上

（2）方法二

森林直接变兄弟，再为二叉树

口诀：兄弟相连，长兄为父，孩子靠左，头根为根

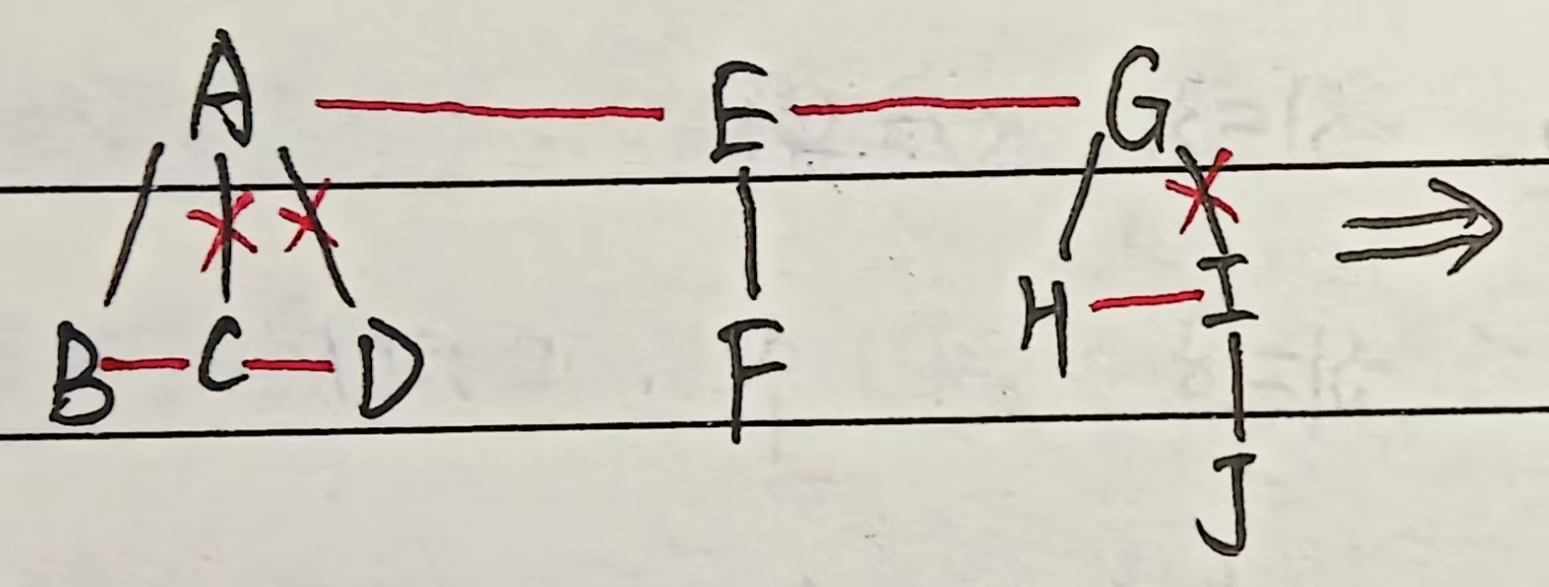
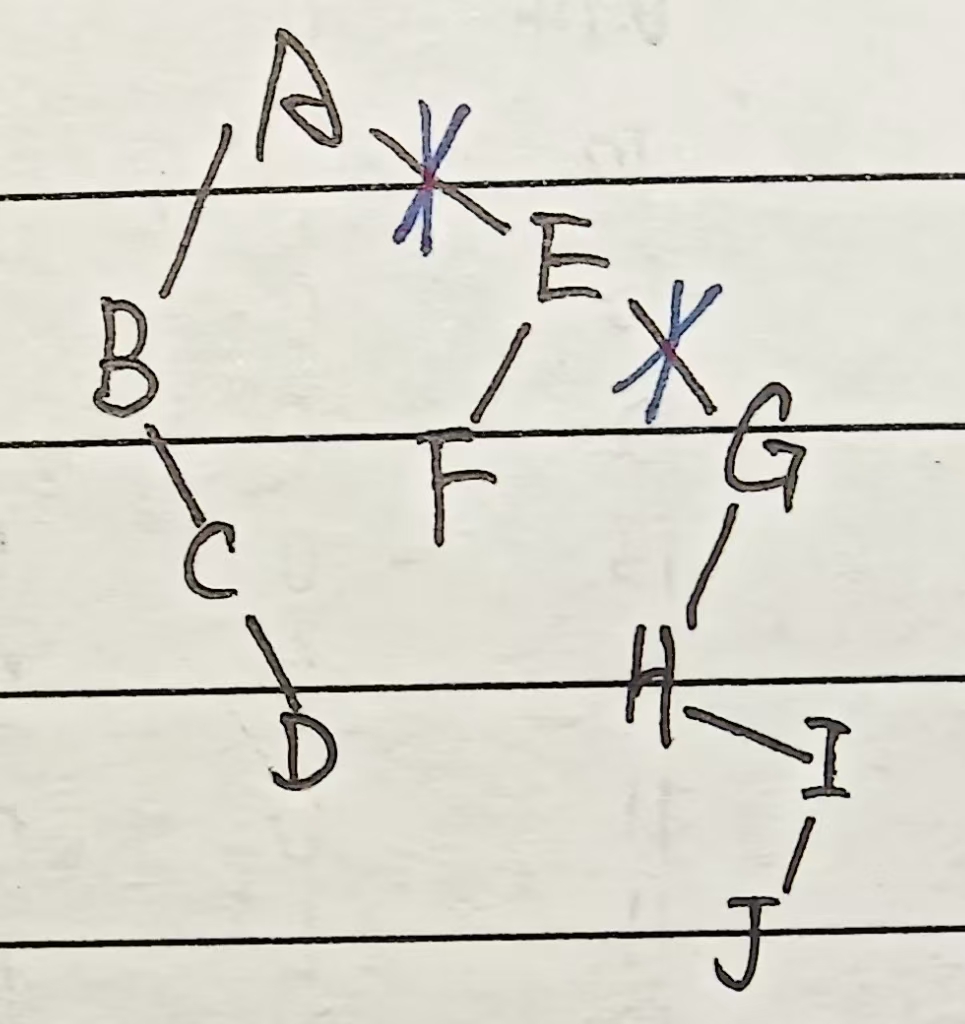
2. 详细介绍

森林（多棵不相交普通树的集合）转化为二叉树，核心是先将森林中的每棵普通树按 "左孩子右兄弟" 法则转为二叉树，再通过 "根节点串联" 将多棵二叉树合并为一棵二叉树，最终形成唯一的二叉树结构。

（1）核心转化步骤

森林转二叉树分为两步：单树转二叉树和多二叉树串联，具体流程如下：

步骤 1：将森林中的每棵普通树转为二叉树

对森林中的每一棵普通树，单独执行 "左孩子右兄弟" 转化法则（与普通树转二叉树规则一致）：

① 节点的第一个孩子作为二叉树的左孩子（左指针指向孩子）。

② 节点的其他孩子依次作为前一个孩子的右兄弟（右指针指向兄弟）。

③ 每棵普通树对应生成一棵独立的二叉树。

步骤 2：将多棵二叉树串联为一棵二叉树

通过 "根节点右指针串联" 合并所有独立的二叉树，规则为：

① 以森林中第一棵树转化后的二叉树作为最终二叉树的 "根树"（即合并后二叉树的根节点为第一棵树的根）。

② 将第二棵树转化后的二叉树，作为 "根树" 根节点的右孩子（用根树的右指针指向第二棵二叉树的根）。

③ 将第三棵树转化后的二叉树，作为第二棵二叉树根节点的右孩子（用第二棵二叉树的右指针指向第三棵二叉树的根）。

④ 依次类推，将所有二叉树按 "前一棵根的右指针指向后一棵根" 的方式串联，最终形成一棵完整的二叉树。

（2）示例说明（以包含 2 棵树的森林为例）

假设森林由以下两棵普通树组成：

① 树 1：根 A，孩子 B、C；B 的孩子 D

② 树 2：根 E，孩子 F、G；G 的孩子 H

第一步：单树转二叉树

① 树 1 转二叉树：

a. A 的第一个孩子 B 作为左孩子，A 的右指针（无兄弟）空。

b. B 的第一个孩子 D 作为左孩子，B 的右指针指向兄弟 C（B 的右孩子 = C）。

c. 结果：A→左 B，B→左 D、右 C；C 无孩子和兄弟。

② 树 2 转二叉树：

a. E 的第一个孩子 F 作为左孩子，E 的右指针指向兄弟 G（E 的右孩子 = G）。

b. G 的第一个孩子 H 作为左孩子，G 的右指针（无兄弟）空。

c. 结果：E→左 F、右 G；G→左 H；F 无孩子和兄弟。

第二步：多二叉树串联

① 以树 1 的二叉树为 "根树"，将树 2 的二叉树根节点 E，作为 "根树" 根节点 A 的右孩子（A 的右指针 = E）。

最终合并后的二叉树结构：

复制代码

3. 转化后的二叉树特性

（1）结构唯一性：每片森林对应唯一的二叉树，且可通过反向规则还原回原森林（先拆分右串联的根节点，再将每棵二叉树还原为普通树）。

（2）根节点差异：与单棵普通树转二叉树不同，森林转二叉树的根节点可能有右孩子（右孩子对应森林中第二棵树的根）。

（3）关系保留：原森林中树与树的 "并列关系"，转化后通过二叉树根节点的 "右指针串联" 体现；树内部的 "孩子 - 兄弟" 关系，仍通过 "左孩子右兄弟" 体现。