直圆锥是一种三维形状,其底部为圆形,表面呈曲面状,逐渐变窄至顶点。圆锥的轴是连接顶点(顶点)和圆形底部中心(中点)的线。该轴垂直于底部,形成直角。
直圆锥的体积公式为V = (1/3) × πr^ 2 h,其中:
- ++r 是基圆锥的半径++
- ++h 是圆锥的高度++
这个公式告诉我们,圆锥的体积是半径和高度相同的圆柱体体积的三分之一。
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
什么是直圆锥?
轴垂直于锥底平面的锥体称为直圆锥体。直圆锥体是一种三维图形,其平面与曲面在顶点处相交。我们可以将直圆锥体想象成以圆柱体为底向外延伸的形状,但随着锥体向上延伸,其半径逐渐减小,直至为零,锥体在该点处闭合。
这个点称为圆锥的顶点,圆形平面称为圆锥的底面。由小边旋转而成的三角形构成一个圆锥。现在,让我们在本文中详细了解正圆锥、它的公式、性质等。
直圆锥定义
如果任何圆锥的轴线垂直于圆锥底面所在的平面,则该圆锥称为直圆锥。我们可以将任意直角三角形沿其底面或高旋转,得到一个直圆锥。
直圆锥的各部分
任何直圆锥都有以下三个部分:
- 底面半径
- 直圆锥高
- 直圆锥的斜高
底面半径:圆锥的圆形底面的底面半径。通常用" r "表示。
直圆锥高 : 定义为直圆锥的高。它是圆心到圆顶的垂直距离。通常用" h "表示。
直圆锥 的斜高:沿圆锥表面测量的圆平面外顶点与底面圆周上一点之间的长度,一般用" l "表示。
直圆锥的底面半径(r)、高(h)、斜高(l)的关系为:
l ****^****2 = h ****^****2 + r ****^****2
直锥体与斜锥体
圆锥体是一种三维形状,类似于三角形,底部为圆形。我们可以根据圆锥体的顶点和底部中心的排列方式,将圆锥体分为两类:
- 右圆锥
- 斜锥体
****直圆锥:****如果圆锥的圆形底面的中心垂直于圆锥的顶点或顶点,则称为直圆锥。
****斜圆锥:****如果圆锥的圆形底面的中心不垂直于圆锥的顶点或顶点,则称为斜圆锥。
下面添加的图像显示了一个直圆锥和一个斜圆锥。
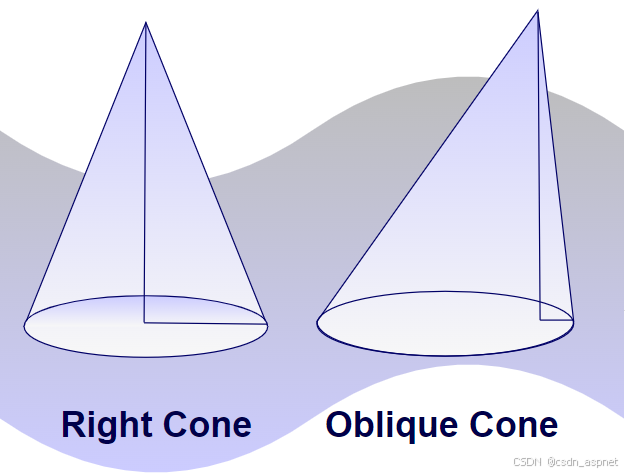
我们还可以通过取一个平行于圆锥底面的平面,并将其与圆锥的曲面相交来判断圆锥的类型。如果交点形状为圆形,则该圆锥为正圆锥。如果交点形状为椭圆形,则该圆锥为斜圆锥。
直圆锥的性质
直圆锥,或简称为直锥,是一种独特的三维形状,具有多种属性。直锥的一些重要属性如下:
- 右圆锥的轴是连接顶点和圆形底座中心的线。
- 直角三角形沿底边或垂线旋转,会生成直圆锥,其中锥体的斜边所生成的面积就是直圆锥的曲面面积。
- 与直圆锥底面平行的平面与直圆锥的表面相交,得到圆。
- 直圆锥的高是圆底面中心到圆锥顶点的垂直距离。
直圆锥的表面积
正圆锥的表面积是三维形状的表面所占据的总面积,以平方厘米 (cm 2 )、平方米 (m 2 ) 等平方单位来测量。正圆锥有两个表面积:
- 曲面面积(CSA)
- 总表面积(TSA)
下图显示了一个直圆锥,其半径为(r),高度为(h),斜高为(l):
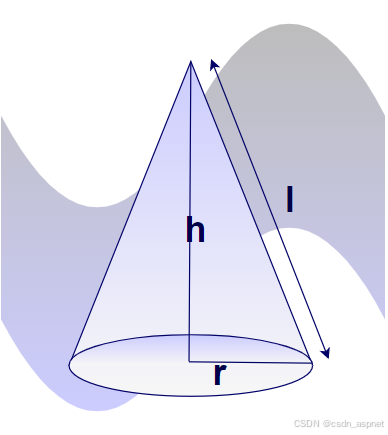
现在我们来详细了解一下直圆锥的CSA和TSA。
直圆锥的曲面面积
直圆锥的侧面积,或称曲面面积,是指直圆锥的曲面所占的区域。计算直圆锥的曲面面积时,不包括底面积。计算直圆锥曲面面积的公式为:
直圆锥的 CSA = πrl 平方单位
我们知道l 2 = h 2 + r 2 ****,****因此圆锥的 CSA 也可以写成:
直圆锥的 CSA = πr√(h^ 2 + r^2 ) 平方单位
在哪里,
- r是底面半径
- l是圆锥的斜高
- h是圆锥的高度
示例:如果一个直圆锥的半径为 28 个单位,高度为 45 个单位,则求该直圆锥的曲面面积。
解决方案:
鉴于,
半径 (r) = 28 个单位
高度 (h) = 45 个单位
我们知道,
圆锥曲面面积= πr√(h^2 + r^2 ) 平方单位
= (22/7) × 28 × √(28^2 + 45^2 )
= 22 × 4 × √(784 + 2025)
= 22 × 4 × √(2809)
= 22 × 4 × 53
= 4664 平方单位。
因此,圆锥的曲面面积为4664平方单位。
直圆锥的总表面积
直圆锥的总表面积等于直圆锥的总面积,包括圆底面积和直圆锥的CSA(截面面积)。计算直圆锥总表面积(TSA)的公式为:
直圆锥的总表面积 (TSA) = 圆底面积 + 直圆锥的 CSA
现在:
- 圆底面积 = πr^2
- 直圆锥的CSA = πrl
TSA = πr^2 + πrl
TSA = πr(r + l)
因此,
直圆锥的总表面积 = πr (r + l) 平方单位
在哪里,
- r是底面半径
- l是圆锥的斜高
例:计算一个直圆锥体的半径和斜高分别为10个单位和11个单位时,其表面积 。(取π = 22/7)
解决方案:
鉴于,
半径 (r) = 10 个单位
倾斜高度 (l) = 11 个单位
我们知道,
右锥体的 TSA = πr(r + l) 平方单位
TSA = 22/7 × 10 × (10 + 11)
= 22 × 30
= 660 平方单位
因此,直圆锥的总表面积为 660 平方单位
直圆锥的体积
正圆锥所占空间的总和定义为正圆锥的体积。我们也可以将正圆锥的体积定义为圆锥所含物质的总质量。圆锥的体积以立方单位表示,例如立方米 (m³ )、立方厘米 (cm³ )等。
直圆锥体积公式
计算直圆锥体积的公式将在下文讨论。假设我们有一个直圆锥,其半径为r,高为h,那么它的体积是同尺寸圆柱体体积的1/3,即
直圆锥的体积 = (1/3) × 圆柱的体积
为了计算直圆锥的体积公式,我们将体积定义为:
直圆锥的体积 = (1/3) × 圆底面积 × 圆锥的高
我们知道这一点。
- 圆底面积 = πr^2
- 圆锥的高=h
V = (1/3) × πr ^2 × h
在哪里,
- r是底面半径
- h是直圆锥的高
其他配方
我们知道圆锥的斜高 (l) = √(r^2 + h^2 )
因此,通过替换直锥体表面积公式中的倾斜值,我们得到
- 直圆锥的曲面面积(CSA)=πr√(r^2 + h^2 )平方单位
- 直圆锥的总表面积 ( TSA ) = πr^2 + πr√(r^2 + h^2 ) 平方单位
直截头圆锥体
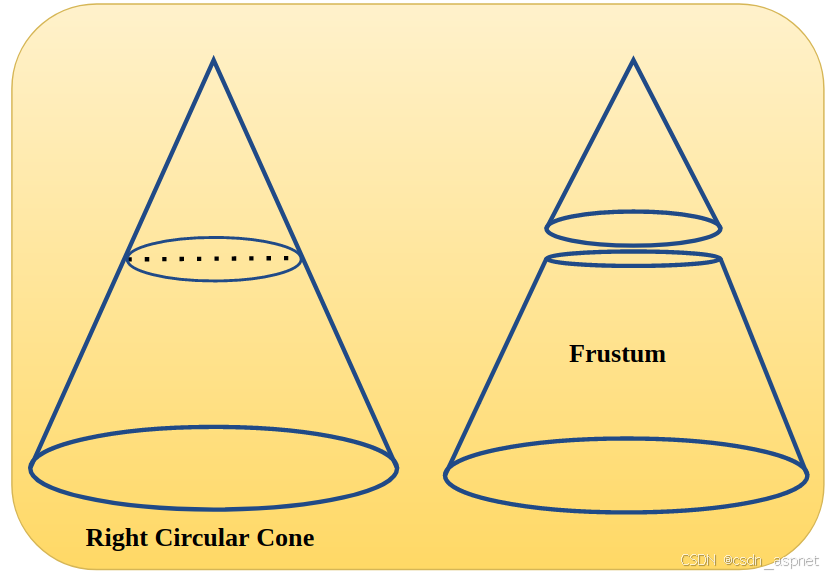
如果我们用平行于其底面的平面切割一个直圆锥体,得到的图形称为直圆锥台。有很多物体都是圆锥台形状的。最常见的类似于直圆锥台的物体是桶。
直圆锥台的体积是通过从大圆锥的体积中减去小圆锥的体积得到的。
直圆锥方程
我们可以用下面讨论的方程来表示三维空间中的正圆锥。设圆锥的顶点在原点,圆锥沿 x、y、z 方向排列,则圆锥的方程为:
(x^2 +y^2 +z^2 )cos^2 θ = (lx + my + nz)^2
在哪里,
- θ表示半垂直角
- (l,m,n)是轴的方向余弦。
直圆锥的例子
以下是现实世界中直圆锥的一些例子:
- 冰淇淋蛋筒:冰淇淋蛋筒是典型的正圆锥体。它顶部尖,底部圆,形成一个锥形,用来盛放冰淇淋。
- 交通锥:道路和建筑工地使用的交通锥通常呈直立圆锥体形状。它们通常呈橙色,顶部尖锐,底部为宽阔的圆形,以保持稳定。
- 派对帽:派对帽通常呈圆锥形,顶部尖,底部圆。通常在庆典和节日期间佩戴。
- 火山:火山的锥形结构通常被描绘成一个直圆锥体。熔岩从顶点喷涌而出,在火山口周围形成一个锥形丘。
- 扬声器:一些扬声器的设计特点是扬声器外壳呈锥形。这种设计有助于将声波向外引导,从而增强音质。
正圆锥解答题
问题1:一个直圆锥的半径和斜高分别为7英寸和13英寸,求其表面积 。(使用π = 22/7)
解决方案:
鉴于
半径 (r) = 7 英寸
倾斜高度 (l) = 13 英寸
我们知道,
直圆锥的表面积 (TSA) = πr(r + l) 平方单位
TSA = 22/7 × 7 × (7 + 13)
= 22 × 20
= 440平方英寸
因此,直圆锥的表面积为 440 平方英寸。
问题 2:如果一个直圆锥的半径为 7 个单位,高度为 24 个单位,求该直圆锥的曲面面积。
解决方案:
鉴于,
半径 (r) = 7 个单位
高度 (h) = 24 个单位
我们知道,
直圆锥的曲面积 (CSA) = πr√(h^2 + r^2 ) 平方单位
CSA = (22/7) × 7 × √(24^2 + 7^2 )
CSA = 22 × √(576 + 49)
CSA = 22 × 25
CSA = 550 平方单位。
因此,直圆锥的曲面面积为 550 平方单位。
问题 3:一个直圆锥的半径为 21 厘米,曲面面积为 660 平方厘米****,求其斜高**** 。(使用 π = 22/7)
解决方案:
鉴于,
直圆锥半径(r)= 14厘米
直圆锥的曲面面积 = 616 平方厘米
设右锥体的斜高为l
我们知道,
直圆锥的曲面面积 = πrl 平方单位
660 = (22/7) × 21 × l
66 × l = 660
长 = 660/66 = 10 厘米
因此,直锥体的斜高为10厘米。
问题 4:如果一个直圆锥的半径为 21 个单位,高度为 8 个单位,求该直圆锥的体积。
解决方案:
鉴于,
半径 (r) = 21 个单位
高度 (h) = 8 个单位
我们知道,
直圆锥的体积 = (1/3) × πr^2 × h
= (1/3) × 22/7 × (21)^2 × 8
= 3696 单元^3
因此,直锥体的体积为 3696 单位^3
直圆锥练习题
- 一个直圆锥的底面半径为6厘米,高为8厘米,这个圆锥的斜高是多少厘米?
- 一个直圆锥体的斜高为10米,半径为4米。圆锥体的总表面积是多少?
- 一个直圆锥的体积是100π立方厘米,半径是5厘米,这个圆锥的高是多少?
- 一个直圆锥,高12英寸,斜高15英寸。它的底面半径是多少?
- 如果一个直圆锥的体积为 200 立方单位,其高度为 10 个单位,那么其底面半径是多少?
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。