算法训练.17 - 技术栈

//在字符串中找出连续最长的字符串
int main() {
    string compare;
    string outcome;
    string str;
    cin >> str;
    for (auto it = str.begin(); it != str.end(); it++)
    {
        if (*it <= '9' && *it >= '0')
        {
            outcome += *it;
            if (it+1<str.end() && *(it + 1) > '9')
            {
                int n = max(outcome.size(), compare.size());
                if (n == outcome.size())
                {
                    compare = outcome;
                    outcome.clear();
                }
                else {
                    outcome.clear();
                }
            }
            //处理一下边界情况，防止访问空指针
            else if ((it + 1 == str.end()) && (*it <= '9' && *it >= '0'))
            {
                int n = max(outcome.size(), compare.size());
                if (n == outcome.size())
                {
                    compare = outcome;
                    outcome.clear();
                }
                else {
                    outcome.clear();
                }
            }
        }
        else {
            ;
        }
    }
    cout << compare << endl;

    return 0;
}

那么咱们再来看着代码进行解析一下：边界情况就是当字符串最后一个是数字的时候，这个时候，你是进不去第一个if的。可以这么说，else if就是为了处理字符串最后一个是数字的这种情况。

80.牛客网-添加逗号

80.1题目解析：

这个题目也很简单，题目要求的是从最低位开始，每三位进行插入，你看见这个，应该就可以想到很多种解法吧。

80.2 算法思路

这里咱们就讲一种思路，就是从尾部开始遍历，反向迭代器（需要注意的是反向迭代器使用的也是++）。反向迭代器，每三位插入逗号，还得处理一下边界情况，就是最后一个位置是不可以插入的，不然就会变成，234，567，345 就会变成这样的了，最前面还有一个逗号，不符合常理。最后全部添加完逗号之后，再反转一下字符串即可

80.3 代码演示

cpp 复制代码

int main() {
    int count = 0;
    string outcome;
    string str;
    cin >> str;
    for (auto it = str.rbegin(); it != str.rend(); it++)
    {
        count++;
        outcome += *it;
        if (it < str.rend() && count == 3)
        {
            //边界情况特殊处理
            if (it == str.rend() - 1)
            {
                ;
            }
            else {
                outcome += ',';
                count = 0;
            }

        }
    }
    reverse(outcome.begin(), outcome.end());
    cout << outcome << endl;
    return 0;
}

81.牛客网-跳台阶

这是今天要讲的第一道动态规划题目，后面应该还会有6道

81.1题目解析：

题目很好理解，接下来咱们直接来看算法思路。

81.2 算法思路：

对于动态规划，之前也讲过应该是4道，咱们再来复习一下思路：状态表示（以哪个位置为结尾，怎么怎么样）-状态转移方程(根据最近几步的状态，推导出状态转移方程）-初始化（一般是根据状态转移方程来确定初始化的，因为要确保不会访问到空的数组嘛）-填表顺序（一般都是从左向右，但肯定有不一般的，咱们今天也会讲到）-返回值（根据dp表的下标来确定这个返回值是怎么回事）。

那么这道题目很明显，状态转移方程为dp[i] = dp[i - 1] + dp[i - 2].其实作者推导状态转移方程的方法就是先写几个特殊值，就是多写几个，然后再根据特殊值推导出泛值。

初始化的话，也好办，需要初始化3个值。

填表是从左向右。

返回值是dp[n-1]，因为咱们要知道，咱们创建的这个dp表的下标其实是从0开始的。

81.3 代码演示

cpp 复制代码

int main() {
    //典型的dp问题
    int n = 0;
    cin >> n;
    vector<int> dp(n + 1, 0);

    if (n == 1)
    {
        cout << 1 << endl;//注意第一个台阶应该是1,不是0
    }
    if (n == 2)
    {
        cout << 2 << endl;
    }
    if (n == 3)
    {
        cout << 3 << endl;
    }
    if (n > 3)
    {
        dp[0] = 1;//1
        dp[1] = 2;//2
        dp[2] = 3;//3
        for (int i = 3; i < n; i++)
        {

            dp[i] = dp[i - 1] + dp[i - 2];
        }
        cout << dp[n - 1] << endl;
    }

    return 0;
}

82.牛客网-扑克牌顺子

82.1题目解析：

其实这道题目的意思就是，0是万能的，可以代替任何的数字。然后给你一个数组，让你判断这个数组里面的值是不是按照顺序依次递增的。

82.2 算法思路：

其实这道题目，作者写的有点冗余，但是还是跟大家说一下我的算法思路吧:

一个连续的数组。5个元素，那么最大值与最小值的之间的差值一定一定是小于5的，这个毋庸置疑。

那么咱们的核心就是判断最小值与最大值的差值是否小于5即可。不管你的数组中有多少个0，都可以这么判断，因为你的0是万能的，可以代替任何数字，咱们只需要判断最大值与除了0之外的最小值的差值即可。还有一点需要注意的是，数组中不可以有连续的数字，否则这个数组就是错误的，直接返回false。（0除外）

83.3 代码演示：

cpp 复制代码

bool IsContinuous(vector<int>& numbers) {
    // write code here
    //首先判断空数组跟数组元素不足5个的，直接去掉
    if (numbers.empty() || numbers.size() != 5) {
        return false;
    }
    int hash[14] = { 0 };
    sort(numbers.begin(), numbers.end());
    for (int i = 0; i < numbers.size(); i++)
    {
        hash[numbers[i]]++;//这个地方只是想算出数组中0的个数是多少
    }
    if (hash[0] == 0)
    {
        for (int i = 1; i < numbers.size(); i++)
        {
            if (numbers[i] == numbers[i - 1])
            {
                return false;
            }
        }
        //你得想到使用差值去计算，即最大的数与最小的数的差值即可。
        if (numbers[numbers.size() - 1] - numbers[0] < 5)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else if (hash[0] == 1)
    {
        for (int i = 1; i < numbers.size(); i++)
        {
            //有连续的数字直接去掉
            if (numbers[i] == numbers[i - 1])
            {
                return false;
            }
        }
        //让最大的与最小的差值小于5，由于有一个1，所以说最小值应该是下标为1的位置
        if (numbers[numbers.size() - 1] - numbers[1] < 5)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else if (hash[0] == 2)
    {
        for (int i = 1; i < numbers.size(); i++)
        {
            //这个的意思是，连续的数字，可以是连续的0，因为这个地方0的数量已经是2个了
            if (numbers[i] == numbers[i - 1] && numbers[i] != 0)
            {
                return false;
            }
        }
        if (numbers[numbers.size() - 1] - numbers[2] < 5)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else if (hash[0] == 3)
    {
        for (int i = 1; i < numbers.size(); i++)
        {
            if (numbers[i] == numbers[i - 1] && numbers[i] != 0)
            {
                return false;
            }
        }
        if (numbers[numbers.size() - 1] - numbers[3] < 5)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else
    {
        return true;
    }
}

83.牛客网-最长回文字串

83.1题目解析：

回文字符串，很经典的问题，咱们也是用很经典的解法，就是随机选取中间值，从中间向两边进行扩散判断是否对称。还有一点需要注意的是这个字串的奇偶问题。

83.2 算法思路：

这个地方需要注意的就一点，就是你的奇偶判断，不需要加if，else，这样进行判读。因为你想一想，你的是子串，子串的话，里面可能你这一次是奇数长度，下一次突然变成偶数长度了，所以你要是if，else，就一棒子打死了。不加if，else，你就直接交给程序就可以了，程序会按照从上到下进行一次一次的判断。（这个很重要）

还有就是奇数长度回文，以单个字符为中心。偶数长度回文，以两个相同字符为中心。

83.3 代码演示：

cpp 复制代码

//这个只是让每一个中心都能得到奇偶的对待。且，不需要加if-else
int getLongestPalindrome(string A) {
    int kk = 0;
    if (A.size() == 1)
    {
        return 1;
    }
    for (int i = 0; i < A.size(); i++)
    {
        // 奇数长度回文，以单个字符为中心
        int left = i;
        int right = i;
        while ((left >= 0 && right < A.size()) && A[left] == A[right])
        {
            left--;
            right++;
        }
        //如果要比较取最大值或者最小值，并且这个值你下一次还得使用，就这样写。里边外边都用你定义的变量即可
        kk = max(right - left -1, kk);
        // 偶数长度回文，以两个相同字符为中心
        left = i;
        right = i + 1;
        while ((left >= 0 && right < A.size()) && A[left] == A[right])
        {
            left--;
            right++;
        }
        kk = max(right - left -1, kk);//至于为什么是right-left-1，这个其实是根据实际看出来的
    }
    return kk;
}

那么为什么是right-left-1呢？不是+1呢？这个其实，假如，因为你的循环条件是大于等于0（left）的时候可以进入，那么这个时候，你left等于0的时候也可以进入，好，这个时候，你再减减不就是负数了吗？那么你减去一个负数，不就是等于正数嘛，就多加了一个1，所以再减去这个1即可。

以下都是动态规划的题目

84.力扣-解码方法

84.1 题目解析：

这个题目很明显的可以看出可以使用动态规划来解决吧，就是可以看出来，这个一整个大问题都是相同的子问题组成的。都是可以将消息分为多少组。

需要注意的是，一个数字前面有前导0的话，这个数字就是错误的，就无法映射。

84.2 算法思路

84.3 代码演示：

cpp 复制代码

//力扣dp问题解码方法
int numDecodings(string s) {
    //创建dp表
    //初始化
    //填表
    //返回值
    int n = s.size();
    vector<int> dp(n);
    //初始化
    if (s[0] != '0')
    {
        dp[0] = 1;//初始化dp表的第一个
    }
    if (n == 1)
    {
        return dp[0];
    }
    if (s[0] != '0' && s[1] != '0') dp[1] += 1;
    int tmp = (s[0] - '0') * 10 + s[1] - '0';
    if (tmp >= 10 && tmp <= 26) dp[1] += 1;//因为不能有前导0，所以只能是10到26

    //填表
    for (int i = 2; i < n; i++)
    {
        if (s[i] != '0') dp[i] += dp[i - 1];
        int tmp = (s[i - 1] - '0') * 10 + s[i] - '0';
        if (tmp >= 10 && tmp <= 26) dp[i] += dp[i - 2];//因为不能有前导0，所以只能是10到26
    }
    return dp[n - 1];
}

85 力扣-不同路径

欧克，接下来进入路径的问题

85.1 题目解析：

初出茅庐的时候，也是有点难呀。作者第一次看到这道题的时候，也是对这个状态转移方程分析了好半天呢。哈哈哈哈，不过幸运的是把状态转移方程给分析出来了。那么这道题，只能向下或者是向右移动，且每次只能移动一格。从左上方移动到右下方，求有多少种路径。

85.2 算法思路：

我记得这类题，在高中的数学里也有，只不过当时的作者智力有限，没有想出好的做法，但是这次不同了，可以使用程序设计做出来。那么动态规划，还是老做法。咱们来看一下，那么dp[m-1][n-1]即为到达m行n列这个地方的所有路径之和。

那么状态转移方程该怎么写呢？来咱们看一下，这个地方说的是，只能移动到下方或者是右方。那么对于一个位置来说，移动到它的所有路径之和，是不是就是到它上方路径加上到它左方的路径之和呀。那么每个位置的路径和的计算方法都是如此。那么如此往复，即可得出状态转移方程为：dp[i][j] = dp[i - 1][j] + dp[i][j - 1].

初始化：这个地方的初始化与一维数组不同，一维数组都是初始化一个数字。但是这个地方你得初始化一行和一列，初始化第一行和第一列。因为你计算的dp[i][j]需要用到上方和左方的值，那么这种情况下，你只能是中间的位置才可以这么计算。其余的位置（就是第一行和第一列）就得初始化了。这个初始化还有坑，初始化行，那么你的i要小于的是列的数量。不是行的，别搞错了。

填表：从上往下，从左往右进行填表

返回值：直接返回dp[m-1][n-1]即可

85.3 代码演示：

cpp 复制代码

int uniquePaths(int m, int n) {
    //创建dp表，这个是二维的
    //状态转移方程
    //初始化
    //填表
    //返回值
    vector<vector<int>> dp(m, vector<int>(n, 0));//创建一个二维数组,注意可以这么创建
    //初始化
    dp[0][0] = 0;
    //由于你看下面的两层for循环，并不能循环到外层的，所以说注意：你初始化的时候，要初始化第一行和第一列
    //初始化第一行
    for (int i = 0; i < n; i++)
    {
        dp[0][i] = 1;
    }
    //初始化第一列
    for (int j = 0; j < m; j++)
    {
        dp[j][0] = 1;
    }

    //填表
    if (m > 1 && n > 1)
    {
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    return dp[m - 1][n - 1];
}

注意一下创建二维数组，并将他们全部初始化为0该怎么写。

86.力扣-不同路径II

86.1 题目解析：

这个题目与前面的不同路径I，几乎一样，唯一不同的是，有了障碍物，并且这个你的路线还不能经过这个障碍物。

86.2 算法思路：

那么这个地方，有了障碍物。障碍物所在的路径全部不能使用。

1.障碍物在行上，是不是这个障碍物之后的行的格子全都不可以使用了？是的！

2.障碍物在列上，是不是这个障碍物下面的列的格子全都不可以使用了？是的！

3.如果障碍物在中间的位置呢？好，这个时候，咱们只需要明白，障碍物如果说在中间，只需要把这个障碍物的位置的dp表里面的值置为0即可。代表，不管你前面走了多少步到这个障碍物这，对不起，为0，你的路白走了。那么中间位置没有障碍物，还是上面的那个状态转移方程即可。

dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

需要注意的是：当障碍物在起点或者是在终点位置的时候，这个时候，还有路径吗？路都给你堵死了。直接返回0.

86.3 代码演示：

cpp 复制代码

int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
    int m = obstacleGrid.size();
    int n = obstacleGrid[0].size();
    for (int i = 0; i < m; i++)
    {
        for (int j = 0; j < n; j++)
        {
            if (obstacleGrid[i][j] == 1) obstacleGrid[i][j] = 'a';
        }
    }
    // 如果起点或终点是障碍物，直接返回0
    if (obstacleGrid[0][0] == 'a' || obstacleGrid[m - 1][n - 1] == 'a') {
        return 0;
    }

    // 使用新的dp数组，避免修改原数组
    vector<vector<int>> dp(m, vector<int>(n, 0));
    dp[0][0] = 0;
    //这个的初始化可能会有点不同，注意障碍物后面的一行或者是一列都是0
    //初始化行的时候，这个i要小于列的长度
    for (int i = 0; i < n; i++)
    {
        if (obstacleGrid[0][i] == 'a')
        {
            for (int o = i; o < n; o++)
            {
                dp[0][o] = 0;
            }
            break;//别忘了break。否则会陷入死循环
        }
        else
        {
            dp[0][i] = 1;
        }

    }
    //初始化列的时候，这个j要小于行的长度
    for (int j = 0; j < m; j++)
    {
        if (obstacleGrid[j][0] == 'a')
        {
            for (int o = j; o < m; o++)
            {
                dp[o][0] = 0;
            }
            break;
        }
        else
        {
            dp[j][0] = 1;
        }
    }
    //填表
    if (m > 1 && n > 1)
    {
        for (int i = 1; i < m; i++)
        {
            for (int j = 1; j < n; j++)
            {
                if (obstacleGrid[i][j] == 'a')
                {
                    dp[i][j] = 0;
                }
                else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
    }
    //返回值
    return dp[m - 1][n - 1];
}

这个地方作者将1全部换成了'a'，也就是97.不过我感觉有点多余了。

87 力扣-珠宝的最高价值

87.1 题目解析：

这个题目很有意思，咱们前面求的是路径的数量是吧。但是这道题目求的不是路径的数量，是什么呢？是每条路径上面值的和。还得是最大值。这个好啊，还得计算每个路径上的和，之后再进行比较。

87.2 算法思路：

根据题目的意思，要求最大值，好，那么咱们创建的dp表，里面的数据，就不存路径的个数和了。存每条路径的和的最大值存到dp表里面，即dp表里面存的就是要求的最大值，最后直接取即可。

那么这个地方，同理，还是得初始化行和列。那么行：你的行的每一格，由于只有一行，所以说只需要加上前一格的数字求和即可。

你的列也是如此。

那么主要是中间的dp[i][j]，这个状态转移方程是什么呢？咱们只需要把【i，j】位置的上方和左方的两个值进行做比较，求出最大值，再加上原来表中【i，j】位置的值是不是就可以了呢？没错！中间的每个位置都可以这么做！所以状态转移方程就出来了：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j]，

不过需要的是这个地方如果说只有一行一列，那么直接返回这个数字即可。

87.3 代码演示：

cpp 复制代码

//这个题目与上面两道题目的区别就在于，上面两道题目求的是路径有多少条。而这道题求的是每条路径上的数字的总和
int jewelleryValue(vector<vector<int>>& frame) {
    int m = frame.size();
    int n = frame[0].size();
    // 建立表格
    vector<vector<int>> dp(m, vector<int>(n, 0));
    // 初始化、
    if (m == 1 && n == 1) {
        return frame[0][0];
    }
    //初始化第一个dp表的数
    dp[0][0] = frame[0][0];
    //初始化行
    for (int i = 1; i < n; i++) {
        dp[0][i] = dp[0][i - 1] + frame[0][i];//需要注意的是这个地方是dp[0][i-1],不是frame[0][i-1]，因为你要加的上一个值是和，和存储在dp表里面
    }
    //初始化列
    for (int j = 1; j < m; j++) {
        dp[j][0] = dp[j - 1][0] + frame[j][0];
    }
    //填表
    if (m > 1 && n > 1) {
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];
            }
        }
    }
    //返回值
    return dp[m - 1][n - 1];
}

88.力扣-下降路径最小和

88.1 题目解析：

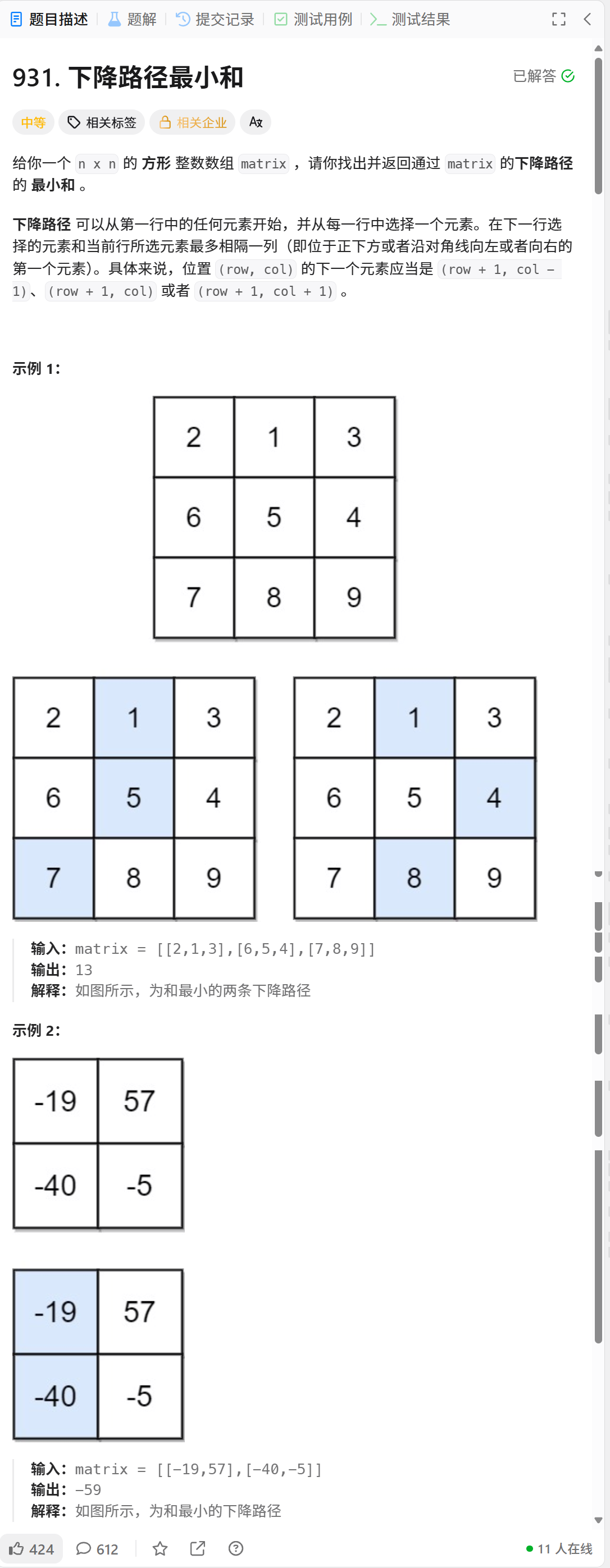
好，这道题目也是求的是路径最小和。只不过跟前面做的有些不同。

88.2 算法思路：

还是先创建一个同等大小的二维dp表，里面存储路径的最小和。

那么：

1.原数组，第一行的数据，你是不是不能动，直接初始化到dp表里里面是不是就可以了。

2.第一列跟最后一列，是特别的，这两列，从第二行开始，第一列：他的数字来源只能是上方跟上方右边的。第二列：他的数字来源只能是上方跟上方左方。并且，还得是dp表这两个格子里面的最小值的那个加上下方那个列里面的数字，才是真正的，就是第一列或者是最后一列的路径最小和。

所以，状态转移方程：第一列：dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + matrix[i][0]

最后一列：dp[i][n - 1] = min(dp[i - 1][n - 1], dp[i - 1][n - 2]) +matrix[i][n - 1]

3.对于中间的位置，比如上方示例一的5，这个位置的路径，可以来自2，1，3这三个位置。所以有三条路径来法。好，那么这个时候，是不是就可以，求出dp表中这三个位置的最小值加上5是不是就是dp表中5这个位置的路径的最小值。

所以，状态转移方程为：dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]),dp[i - 1][j + 1]) +matrix[i][j]

那么最后，最后一行是不是就是咱们想要的所有路径的最小和。咱们只需要在最后一行了里面抽出来一个最小的即可。

88.3 代码演示：

cpp 复制代码

int minFallingPathSum(vector<vector<int>>& matrix) {
    int minoutcome = INT_MAX;
    // 创建一个二维数组表
    // 初始化
    // 状态转移方程
    // 填表
    // 返回值
    int n = matrix.size();
    //0行0列的情况得初始化一下
    if (n == 1) {
        return matrix[0][0];
    }
    vector<vector<int>> dp(n, vector<int>(n, 0)); // 创建一个二维数组表
    // 它给了n*n，所以不需要担心单独一列的情况
    // 初始化
    for (int i = 0; i < n; i++) {
        dp[0][i] = matrix[0][i];
    }
    // dp表里面我只要最小的，其他的都不要
    //这个填表要注意中间的跟最左边，最右边的填表方式不一样
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (j == 0) {
                dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + matrix[i][0];
            }
            else if (j == n - 1) {
                dp[i][n - 1] = min(dp[i - 1][n - 1], dp[i - 1][n - 2]) +matrix[i][n - 1];
            }
            else {
                dp[i][j] = min(min(dp[i - 1][j], dp[i - 1][j - 1]),dp[i - 1][j + 1]) +matrix[i][j];
            }
        }
    }
    //最后再比较最后一行，拿出你想要的结果即可
    for (int i = 1; i < n; i++) {
        minoutcome = min(min(dp[n - 1][i], dp[n - 1][i - 1]), minoutcome);
    }
    return minoutcome;
}

89.力扣-最小路径和

89.1题目解析：

这道题目，我可以毫不夸张的说，就是跟上面的那个"珠宝"的那道题目几乎一模一样。

只不过珠宝求的是最大值，这里求的是最小值。

89.2 算法思路

这不就是珠宝的那道题目的代码把主循环里面的min改为max即可。

89.3 代码演示：

cpp 复制代码

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size();
    int n = grid[0].size();
    // 建立表格
    vector<vector<int>> dp(m, vector<int>(n, 0));
    // 初始化、
    if (m == 1 && n == 1) {
        return grid[0][0];
    }
    // 初始化第一个dp表的数
    dp[0][0] = grid[0][0];
    // 初始化行
    for (int i = 1; i < n; i++) {
        dp[0][i] = dp[0][i - 1] + grid[0][i]; // 需要注意的是这个地方是dp[0][i-1],不是grid[0][i-1]，因为你要加的上一个值是和，和存储在dp表里面
    }
    // 初始化列
    for (int j = 1; j < m; j++) {
        dp[j][0] = dp[j - 1][0] + grid[j][0];
    }
    // 填表
    if (m > 1 && n > 1) {
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
    }
    // 返回值
    return dp[m - 1][n - 1];
}

90.力扣-地下城游戏

90.1 题目解析：

哎呦我的天哪，这道题可把我坑惨了。为什么这么说，咱们待会再说。这道题目，本质就是求最小，但是不同的是，这个地方的骑士血量不可以小于等于0.

90.2 算法思路：

好，那么咱们还是像往常一样：[i,j]表示以[i,j]位置为结尾，巴拉巴拉。好，那么就是以【0，0】为开始。你如果这样的话，你做去吧，我一开始就是这么做的，你会发现，后面的都是未知状态，就是你也无法给出一个准确的血量，去完整的通关。因为后面你怎么通关，都是未知的。我说的可能有点意思不太明白。大家再体会一下。

所以，咱们得反着来，就是【i，j】位置为起点，【0，0】位置为结尾。

那么咱们的状态转移方程该如何确定呢？

咱们还是以某个位置，向右或者是向下进行出发。

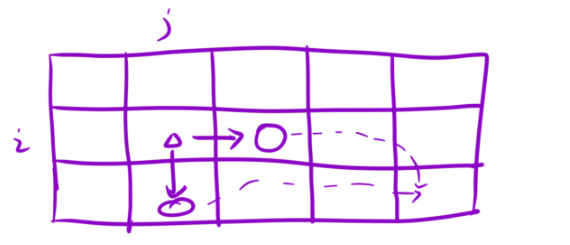
那么此时，假设[i,j]位置的为x，那么你要是想走到右边，你是不是得先走出去（这个很重要），所以说（原数组设为d），x+d[i][j]>=dp[i][j+1]。那么移项。x>=dp[i][j+1]-d[i][j]。好，又因为你的取的是最小值，所以说x=dp[i][j+1]-d[i][j].。即dp[i][j]=dp[i][j+1]-d[i][j]。同理，下面的一样：

dp[i][j]=dp[i+1][j]-d[i][j]（两种情况）。又因为，dp[i][j]也要取最小值，所以说dp=min(dp[i][j+1],dp[i+1][j])-d[i][j]。

那么这个地方涉及到一个问题，就是假如，d[i][j]特别大，那么你的dp[i][j[这个时候不就是负的嘛？那你的dp[i][j]是负的，它是怎么进来【i，j】这个位置的呢？所以说，还得加一个状态转移方程：dp[i][j] = max(1, dp[i][j])，

所以说，状态转移方程就确定了：dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];

dp[i][j] = max(1, dp[i][j]);

初始化：这个地方的初始化得这样初始化：

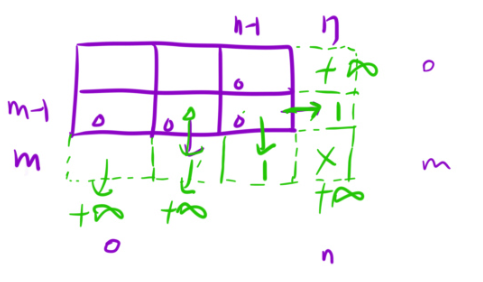
由于咱们要保证到最后一个即m-1行，n-1列，也可以走，那么这个时候，它的下面右边设置为多少呢？1就可以。它只要能走出来，就设置为1.

那么除了这两个位置，添加的行和列的其余位置全部初始化为INT_MAX。因为，假如上面的2行2列这个位置，这个地方只能往右边走吧，但是由于咱们还添加了一行，所以这个位置，它得进行比较才可以。比较出最小的。又因为只能往右走，所以说，下面的那个只能设置为INT_MAX。其余的位置同理。

这个填表需要注意的是：从下往上，从右往左。

返回值就是【0，0】这个位置的值即可。

90.3 代码演示：

cpp 复制代码

int calculateMinimumHP(vector<vector<int>>& dungeon)
{
    int m = dungeon.size(), n = dungeon[0].size();
    // 建表+初始化

     vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
     //这里初始化为INT_MAX的目的是什么呢？就是确保能正确填表
     //例如，最下面除了新添加的一行之外的最后一行，那么接下来只能往
     //右边移动，但是由于下面还有一行，而咱们需要判断的是min值。所以说
     //把下面的一个设置为INT_MAX即可。
    dp[m][n - 1] = dp[m - 1][n] = 1;
    //这里设置为1是为了，dp[m-1][n-1]这个位置也可以继续移动，假设能出来，那么最小的
    // 血量就是1
    // 填表（从下往上，从右往左填表）
        for (int i = m - 1; i >= 0; i--)
            for (int j = n - 1; j >= 0; j--)
            {
                dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
                dp[i][j] = max(1, dp[i][j]);//如果说dungeon[i][j]这个位置的值，就是血包
                //特别的大，那么此时，上面的式子就是一个负数了，而负数的话，就已经死了啊，
                //怎么还能继续往下走呢？所以说这里还得进行判断一下，如果是负数的话，直接
                //让它等于1即可。正数则不需要管
            }
    // 返回结果
       return dp[0][0];
}

ok，本篇算法到此结束.................