并查集
主要处理一些不相交集合的合并问题
经典应用:最小生成树(Kruskal)算法 ,最近公共祖先 ,朋友圈关系统计
基础
将编号分别为1-n的n个对象划分为不相交集合,在每个集合中选择其中某个元素代表所在集合。
基本操作 ,并查集的合并优化 ,并查集的查询优化----路径压缩,带权值并查集。
基本操作
定义数组 s[],开始时,还没处理点与点之间的连接关系,所以每个点属于独立的集,直接以元素表示它的集s[i],如元素1的集为s[1]
- 初始化
cpp
const int N=100005;
int s[N];
void init_set(){
for(inti=1;i<=N;i++) s[i]=i;
}- 查找
cpp
int find_set(int x){
return x==s[x]?x:find_set(s[x]);
}优化 路径压缩
cpp
int find_set(int x){
if(x!=s[x]) s[x]=find_set(s[x]); //在查找3的同时进行赋值操作,实现路径压缩。下次再找可在O(1)时间复杂度内完成
return s[x]; //注意,不能返回x,因为if里面的执行完了要返回s[x]作为查询结果,这里并不是else,不一定x==s[x]才执行。
}非递归路径压缩算法
cpp
int find_set(int x){
int r=x;
while(s[r]!=r) r=s[r];
int i=x,j;
while(i!=r){
j=s[i];
s[i]=r;
i=j;
}
return r;
}在做路径压缩时,附带地优化了合并。
并查集的合并和查询优化,实际上是在改变树的形状,把原来"细长"的,操作低效的大量小树,变为"粗短"的,操作高效的少量"大树"。
- 合并
cpp
void merge_set(int x,int y){
x=find_set(x);
y=find_set(y);
if(x!=y) s[x]=s[y]; //将x所在"树"合并到y所在"树"
//if(x!=y) s[find_set(x)]=s[find_set(y)];
}示意:
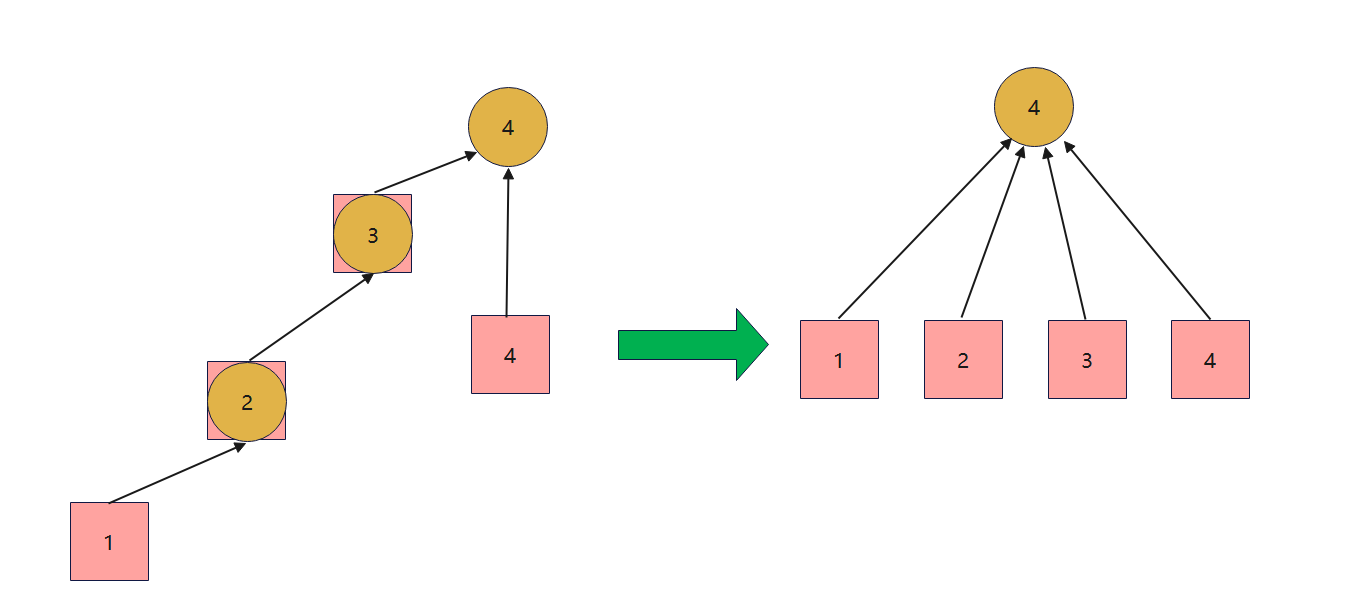
模版代码封装
cpp
class DisjointSet {
vector<int>s;
int cnt;
public:
DisjointSet(int n) {
s.resize(n);
cnt = n;
iota(s.begin(), s.end(),0);
}
int find_set(int t) { //查找
if (t != s[t]) s[t] = find_set(t);
return s[t];
}
void merge_set(int x, int y) { //合并
x = find_set(x);
y = find_set(y);
if (x != y) {
s[x] = s[y];
cnt++; //每两个集合合并,独立区间总数-1
}
}
int count() {
return cnt;
}
};带权值并查集
定义一个数组d[],把父节点的权值记为d[i]。
以相加关系为例
cpp
int find_set(int x){
if(x!=s[x]){
int t=s[x];
s[x]=find_set(s[x]);
d[x]+=d[t];
}
return s[x];
}并查集还有一些更复杂的应用,如:可持续化并查集,可撤销并查集等。
统计连通分量
合根植物
蓝桥杯2017年国赛题
一个植物园里有n株植物,它们会两两合根为一株,给定他们的合根情况,问合根后有多少株植物?
第一行输入n代表起始植物数,第二行输入k,代表后面有k行数据
后面k行,每行输入两个整数a,b,表示植物a和植物b合根。
输出一个整数代表合根后有多少株植物。
思路分析
这可以算是并查集的模版题了,起初每个植物的根都是独立的,共n株植物,若两植物可以合根,总的将减少一株植物数,最后维护的那个统计值就是答案。
cpp
#include <bits/stdc++.h>
using namespace std;
vector<int>d;
int find(int x){
if(x!=d[x]) d[x]=find(d[x]);
return d[x];
}
int main()
{
// 请在此输入您的代码
int cnt;
cin>>cnt;
d=vector<int>(cnt+1);
for(int i=1;i<=cnt;i++) d[i]=i; //初始化并查集
int k; cin>>k;
int ans=cnt;
while(k--){
int a,b; cin>>a>>b;
int x=find(a),y=find(b);
if(x!=y){ //每两株不同根植物合并,总数-1.
ans--;
d[find(a)]=d[find(b)]; //合并
}
}
cout<<ans;
return 0;
}包含k个连通分量需要的最短时间
问题描述
给你一个整数 n,表示一个包含 n 个节点(从 0 到 n - 1 编号)的无向图。该图由一个二维数组 edges 表示,其中 edges[i] = [ui, vi, timei] 表示一条连接节点 ui 和节点 vi 的无向边,该边会在时间 timei 被移除。
同时,另给你一个整数 k。
最初,图可能是连通的,也可能是非连通的。你的任务是找到一个 最小 的时间 t,使得在移除所有满足条件 time <= t 的边之后,该图包含 至少 k 个连通分量。
返回这个 最小 时间 t。
连通分量 是图的一个子图,其中任意两个顶点之间都存在路径,且子图中的任意顶点均不与子图外的顶点共享边。
思路分析
题目其实是问:求最小的t,使得去除所有权值小于等于 t 的边后图中至少有k个连通分量。
当 t 越大,能划分出的连通分量越多,越能符合要求,问题具有单调性,可以用二分答案来解决。
每次二分猜答案为mid,根据mid去除所有边权小于等于mid的边,使用并查集统计连通分量。
代码
cpp
int minTime(int n, vector<vector<int>>& edges, int K) {
int root[n];
auto findroot = [&](this auto &&findroot, int x) -> int {
if (root[x] != x) root[x] = findroot(root[x]);
return root[x];
};
auto check = [&](int lim) {
for (int i = 0; i < n; i++) root[i] = i; //初始化并查集
for (auto &edge : edges) if (edge[2] > lim) {
int x = findroot(edge[0]), y = findroot(edge[1]);
if (x != y) root[x] = y; //并查集和根操作
}
int cnt = 0;
for (int i = 0; i < n; i++) if (findroot(i) == i) cnt++; //统计连通分量
return cnt >= K;
};
int head = 0, tail = 0;
for (auto &edge : edges) tail = max(tail, edge[2]);
while (head < tail) { //二分查找最小的答案
int mid = (head + tail) >> 1;
if (check(mid)) tail = mid;
else head = mid + 1;
}
return head;
}其他应用
新增道路查询后的最短距离 II
问题描述
给你一个整数 n 和一个二维整数数组 queries。
有 n 个城市,编号从 0 到 n - 1。初始时,每个城市 i 都有一条单向 道路通往城市 i + 1( 0 <= i < n - 1)。
queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向 道路。每次查询后,你需要找到从城市 0 到城市 n - 1 的最短路径 的长度。
所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。
返回一个数组 answer,对于范围 [0, queries.length - 1] 中的每个 i,answer[i] 是处理完前 i + 1 个查询后,从城市 0 到城市 n - 1 的最短路径的长度。
思路分析
所有查询中不会存在 两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1],意味着新建的单项道路不存在交叉。每新建一条道路,执行道路归并操作。
定义并查集f,初始时f[i]表示边i--->i+1,f[i]=i;1每新建一条单向道路u--->v,将[u,v-2]范围内的边都归入到边v-1上
如{2,4},将f[2],f[3]都等于f[4].表示将2,3边都归到4边。此时最短路径减2。
定义变量ans统计总的边数,每归入一条边说明路径简化一条,ans--;每次新建一条单向道路,将统计完后ans存入目标数组。
代码
cpp
vector<int>f;
int find(int i){
if(f[i]!=i) f[i]=find(f[i]);
return f[i];
}
vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
f=vector<int>(n-1);
iota(f.begin(),f.end(),0); //初始化并查集f
int size=queries.size();
vector<int>tr(size); //答案
int ans=n-1;
for(int i=0;i<size;i++){
int l=queries[i][0],r=queries[i][1]-1; //边[l,r-2]并入到边r-1
int ft=find(r);
for(int j=find(l);j<r;j=find(j+1)){
f[j]=ft;
ans--; //每次减一,说明优化掉了一段单位道路
}
tr[i]=ans;
}
return tr;
}兔子集结
蓝桥杯2024年国赛题
有n个兔子排成一队,准备一场集结跳跃活动。第i个兔子其位置为pi。
兔子每次跳跃,只能向左或向右移动一个单位距离。当两只相互靠近的兔子之间的距离为1时,左边的兔子会停止,右边的兔子会跳到左边兔子的位置上,完成集结。兔子们会一直跳跃,直到与自己最初选择的同伴完成集结后停止。问:所有兔子完成集结后,每只兔子都分别位于哪个位置上?
思路分析
可以把兔子集结抽象成并查集的合根操作,两只兔子集结在同一个位置就是两个集合并 在一起。另外维护一个答案数组ans,ans[i]记录第i个兔子的最终位置。
代码
cpp
#include <bits/stdc++.h>
#define val first
#define index second
using namespace std;
vector<int>f;
void init(int n){
f.resize(n);
iota(f.begin(),f.end(),0);
}
int find_set(int x){
if(x!=f[x]) f[x]=find_set(f[x]);
return f[x];
}
int main()
{
int n; cin>>n;
vector<pair<int,int>>p(n);
int cnt=0;
for(auto &i:p){
cin>>i.val;
i.index=cnt++;
}
sort(p.begin(),p.end());
vector<int>ans(n);
init(n);
f[0]=1;
for(int i=1;i<n;i++){
if(i==n-1||p[i].val-p[i-1].val<=p[i+1].val-p[i].val){ //向左移动
if(find_set(i-1)==i){ //两边相互靠拢
ans[p[i].index]=(p[i].val+p[i-1].val)/2;
}
else{
f[i]=find_set(i-1);
}
}else{ //向右移动
f[i]=find_set(i+1);
}
}
for(int i=0;i<n;i++){ //根据最终的并查集,获得最终的结果
if(f[i]!=i) ans[p[i].index]=ans[p[find_set(i)].index]; //当前第i个兔子原始是第p[i].index个
}
for(int i:ans) cout<<i<<" ";
return 0;
}