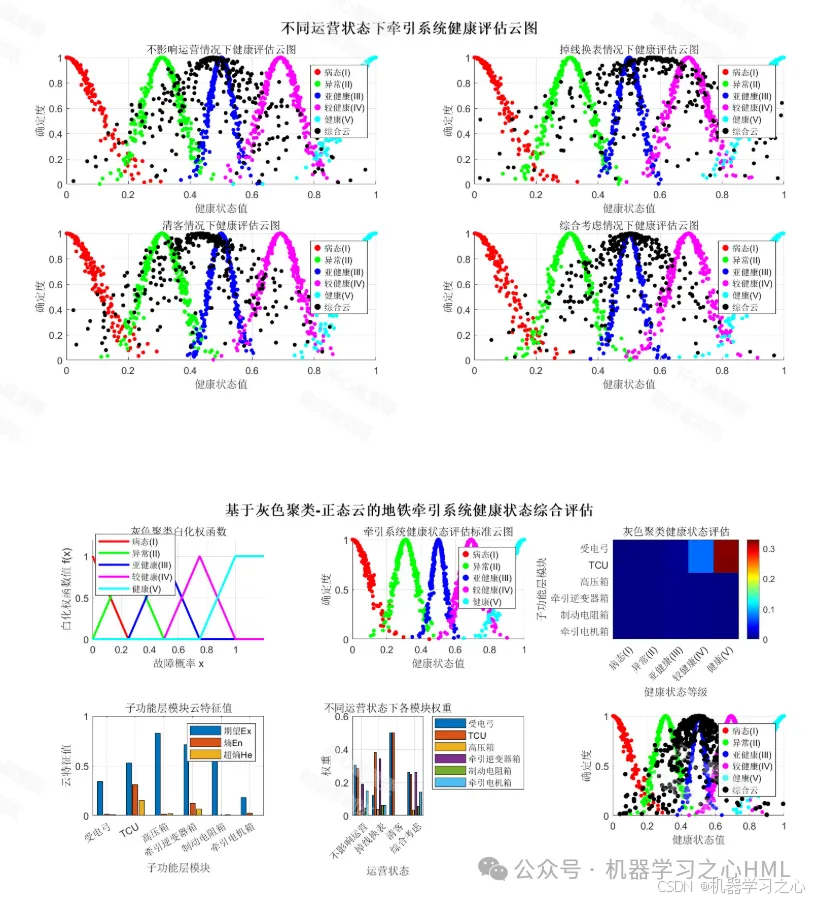
一、 引言:问题背景与模型优势
1. 问题背景:
地铁牵引系统是列车的"心脏",其健康状态直接关系到运营安全、效率和成本。其状态评估面临以下挑战:
- 多源性不确定性: 系统状态既存在"亦此亦彼"的模糊性(如"轻微老化"),也存在因测量误差、随机干扰等带来的随机性。
- 信息不完全(灰色性): 很难获得反映系统健康状态的全部信息,部分信息明确,部分信息未知。
- 多指标综合: 健康状态需从电气、机械、热、控制等多个维度的指标综合评判。
2. 模型优势:
- 灰色聚类: 擅长处理"小样本、贫信息"问题,通过白化权函数将不完全信息定量化,实现对各评估指标的分类。
- 正态云模型: 通过期望(Ex)、熵(En)、超熵(He)三个数字特征,完美刻画概念的模糊性和随机性,实现定性概念与定量数值之间的不确定性转换。
- 结合价值: 灰色聚类解决了指标分类问题,而正态云模型则优化了分类边界的"硬划分",使评估结果更符合工程实际,容错性更强,评估结果更可靠。
二、 评估模型构建步骤
步骤一:确定评估指标体系与健康状态等级
-
建立评估指标集 (U):
选取能全面反映牵引系统健康状态的关键参数。例如:
U1:牵引电机电流谐波畸变率U2:牵引逆变器IGBT模块结温波动U3:直流侧电压波动率U4:齿轮箱振动加速度有效值U5:控制单元故障码触发频率- ... (可根据实际系统扩充)
-
确定健康状态等级集 (V):
V1:健康V2:良好V3:注意V4:恶化V5:危险
(通常分为4-5个等级)
步骤二:构建正态云模型 for 各指标的灰类
对于每个评估指标Ui 的每个健康等级Vj,都构建一个正态云模型。这是模型的核心。
-
确定等级界限值:
根据国家标准、行业规范、历史数据和专家经验,确定每个指标在不同健康等级的临界值。假设指标Ui对于等级Vj的界限区间为
[Aij1, Aij2]。 -
计算正态云数字特征:
- 期望 (Ex): 该区间的中心值。
Ex = (Aij1 + Aij2) / 2 - 熵 (En): 代表概念的模糊度,即区间可接受的取值范围。通常取
En = (Aij2 - Aij1) / 6(基于"3En原则")。 - 超熵 (He): 代表熵的不确定性(即模型的随机性)。可根据数据的离散程度或经验设定,如取
He = k * En(k是一个远小于1的常数,如0.01~0.1),或通过逆向云发生器从历史数据中获取。
- 期望 (Ex): 该区间的中心值。
举例: 假设"牵引电机电流谐波畸变率(U1)"的"注意(V3)"等级区间为 [5%, 10%]。
Ex = (5 + 10) / 2 = 7.5En = (10 - 5) / 6 ≈ 0.833He可设定为0.05(根据经验)
重复此过程,为所有指标的所有等级构建云模型,形成"指标-等级"云模型矩阵。
步骤三:确定各指标权重集 (W)
采用主观与客观相结合的方法(如AHP+熵权法)确定权重,以平衡专家知识和数据本身的信息量。
W = [w1, w2, ..., wm],其中∑wi = 1,m是指标个数。
步骤四:采集数据与聚类系数计算(灰色聚类)
-
采集实测数据:
获取被评估牵引系统在当前时刻的各指标实测值,记为向量
X = [x1, x2, ..., xm]。 -
计算灰色聚类系数 (σij):
- 传统灰色聚类使用白化权函数。在这里,我们用正态云的确定度来代替白化权函数。
- 对于指标
Ui的实测值xi,计算它属于每个健康等级Vj的确定度 μj(xi) 。- 生成一个以
En为期望,He为标准差的正态随机数:En' = NormRand(En, He) - 计算确定度:
μj(xi) = exp( - (xi - Ex)^2 / (2 * (En')^2) )
- 生成一个以
- 注: 由于
He引入了随机性,单次计算有波动。为提高稳定性,需进行N次(如1000次)重复计算,取平均值作为最终的确定度:μ_j_avg(xi) - 则指标
Ui对等级Vj的聚类系数为:σij = μ_j_avg(xi)
-
构建聚类系数矩阵 (Σ):
Σ = [ σ11 σ12 ... σ1n ] [ σ21 σ22 ... σ2n ] [ ... ... ... ... ] [ σm1 σm2 ... σmn ]其中,
n是健康等级数。
步骤五:综合聚类评估与结果判定
-
计算综合聚类向量 (Z):
将权重向量
W与聚类系数矩阵Σ相乘,得到被评估对象对各健康等级的综合隶属度向量Z。
Z = W × Σ = [z1, z2, ..., zn]其中,
zj = ∑ (wi * σij),i=1 to m -
健康状态判定:
- 最大隶属度原则: 找出
Z中最大的元素zk = max{z1, z2, ..., zn},则判定该牵引系统的健康状态为Vk。 - 加权评分原则(可选): 为每个等级
Vj赋予一个分数Sj(如:健康=100,良好=80,注意=60,恶化=40,危险=20),则综合得分为Score = ∑ (zj * Sj)。根据得分区间最终确定状态。
- 最大隶属度原则: 找出
三、 实例
假设:
-
指标:仅用
U1(谐波畸变率)和U5(故障码频率)。 -
等级:
V1(健康),V2(良好),V3(注意)。 -
权重:
W = [0.6, 0.4](认为U1更重要)。 -
云模型参数(已通过步骤二建立):
指标 等级 Ex En He U1 V1 2.0 0.333 0.03 U1 V2 4.5 0.500 0.05 U1 V3 7.5 0.833 0.08 U5 V1 0.1 0.067 0.01 U5 V2 0.5 0.167 0.02 U5 V3 1.5 0.500 0.05
评估过程:
-
实测数据:
x1 = 5.2%(U1),x5 = 0.8次/小时(U5)。 -
计算聚类系数(通过1000次云发生器循环取平均):
-
对于
U1=5.2:μ1(5.2) ≈ 0.05(属于V1的可能很低)μ2(5.2) ≈ 0.65(属于V2的可能较高)μ3(5.2) ≈ 0.45(属于V3的可能也存在)
-
对于
U5=0.8:μ1(0.8) ≈ 0.00μ2(0.8) ≈ 0.55μ3(0.8) ≈ 0.70
-
聚类系数矩阵
Σ:Σ = [ 0.05 0.65 0.45 ] [ 0.00 0.55 0.70 ]
-
-
综合聚类评估:
Z = W × Σ = [0.6, 0.4] × Σ = [0.6*0.05+0.4*0.00, 0.6*0.65+0.4*0.55, 0.6*0.45+0.4*0.70] = [0.03, 0.61, 0.55]
Z = [0.03, 0.61, 0.55] -
结果判定:
- 最大隶属度
max(Z) = 0.61,对应等级V2(良好)。 - 同时,我们看到对
V3(注意)的隶属度(0.55)也很高,这给出了一个重要的预警信息:系统虽然总体评为"良好",但有向"注意"状态发展的明显趋势,需要密切关注。
- 最大隶属度
四、 结论
本模型基于灰色聚类-正态云的地铁牵引系统健康状态评估方法,具有以下特点:
- 理论先进: 同时处理了评估过程中的模糊性和随机性,比单一模型更符合工程实际。
- 评估精准: 云模型的引入使得等级边界具有"软过渡"特性,评估结果不再是简单的非此即彼,更能反映系统的渐变过程。
- 预警性强: 如实例所示,综合聚类向量
Z不仅能给出最终结论,还能通过分析各隶属度的大小关系,有效预测系统的状态发展趋势,实现早期预警。 - 实用性好: 模型结构清晰,可编程实现,适用于地铁运维现场的在线或离线智能评估系统。