Matlab学习记录14

崇山峻岭之间2025-12-26 9:29

书籍：Matlab实用教程

工具：Matlab2021a

在线工具：https://www.cainiaojc.com/tool/octave/

缺少一些包

在线工具：https://octave-online.net/

比较健全。

电脑信息：Intel® Xeon® CPU E5-2603 v3 @ 1.60GHz

系统类型：64位操作系统，基于X64的处理器 windows10 专业版

第6章 线性控制系统分析与设计

6.1. 线性系统的描述

6.1.1 状态空间描述法

复制代码 
wn=1;
A=[0 1;-wn^2 -2*zeta*wn];
B=[0;wn^2];
C=[1 0];
D=0;
G=ss(A,B,C,D)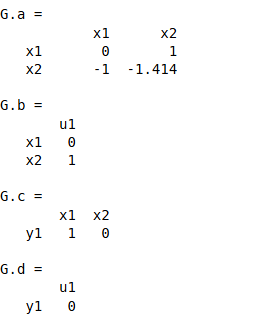

6.1.2 传递函数描述法

复制代码 
num=1;
den=[1 1.414 1];
G=tf(num,den)

6.1.3 零-极点描述法

复制代码 
num=1;
den=[1 1.414 1];
z=roots(num)
p=roots(den)
zpk(z,p,1)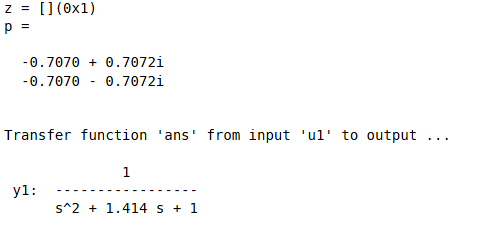
复制代码 
num=1;
den=[1 1.414 1];
z=roots(num)
p=roots(den)
[r,p,k]=residue(num,den)

6.1.4 离散系统的数学描述

1、状态空间描述法

复制代码 
a=[-1.5 -0.5;1 0];
b=[1;0];
c=[0 0.5];
d=0;
G=ss(a,b,c,d,0.1)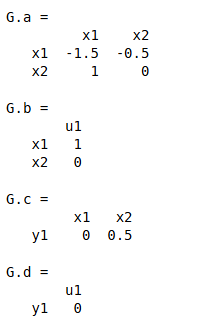

2、脉冲传递函数描述法

复制代码 
num1=[0.5 0];
den=[1 -1.5 0.5];
G1=tf(num1,den,-1)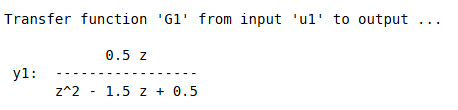
复制代码 
num2=[0 0.5];
den=[1 -1.5 0.5];
G2=filt(num2,den)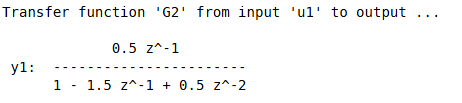

3、零-极点增益描述法

复制代码 
G3=zpk([0],[0.5 1],0.5,-1)

6.2 线性系统模型之间的转换

6.2.1 连续系统模型之间的转换

1、系统模型的转换

A、状态空间模型的获得

复制代码 
num=[0 3 2;1 2 3];
den=[3 5 2 1];
G11=tf(num(1,:),den)
G12=tf(num(2,:),den)
G=ss([G11;G12])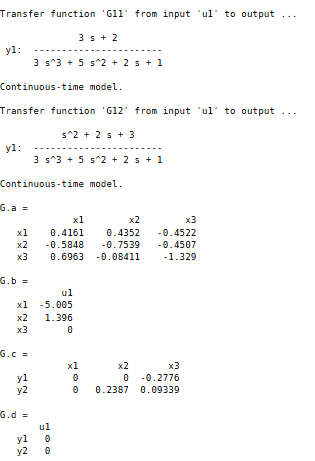

B、传递函数的获得：

复制代码 
num=[0 3 2;1 2 3];
den=[3 5 2 1];
G11=tf(num(1,:),den)
G12=tf(num(2,:),den)
G=ss([G11;G12])
G1=tf(G)


C、零-极点模型的获得

复制代码 
num=[0 3 2;1 2 3];
den=[3 5 2 1];
G11=tf(num(1,:),den)
G12=tf(num(2,:),den)
G=ss([G11;G12])
G1=tf(G)
G2=zpk(G)
G3=zpk(G1)


2、模型参数的获取

复制代码 
num=[0 3 2;1 2 3];
den=[3 5 2 1];
G11=tf(num(1,:),den)
G12=tf(num(2,:),den)
G=ss([G11;G12])
G1=tf(G)
G2=zpk(G)
G3=zpk(G1)
[a,b,c,d]=ssdata(G1)
[num,den]=tfdata(G2)
[z,p,k]=zpkdata(G)






3、模型类型的检验

继续上面的实例：

复制代码 
class(G)

ans = ss

isa(G,'tf')

ans = 0

6.2.2 连续系统与离散系统之间的转换

1、c2d命令

复制代码 
a=[0 1;-1 -1.414];
b=[0;1];
c=[1 0];
d=0;
G=ss(a,b,c,d);
Gd=c2d(G,0.1)

2、d2c命令

复制代码 
G=d2c(Gd)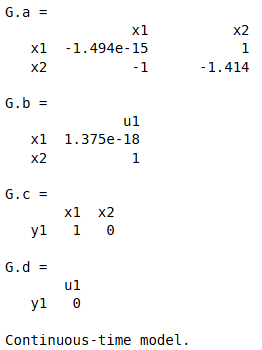

3、d2d命令

复制代码 
Gd2=d2d(Gd,0.3)

6.2.3 模型对象的属性

1、模型对象的属性

2、get命令和set命令

复制代码 
num=1;
den=[1 1.414 1];
G=tf(num,den);
get(G)

        num:  p-by-m cell array of row vectors (m = number of inputs) 
        den:  p-by-m cell array of row vectors (p = number of outputs)
      tfvar:  string (usually s or z)                                 
        inv:  logical (true for negative powers of TF variable)       
       tsam:  scalar (sample time in seconds)                         
     inname:  m-by-1 cell vector of strings                           
    outname:  p-by-1 cell vector of strings                           
    ingroup:  struct with indices as fields                           
   outgroup:  struct with indices as fields                           
       name:  string                                                  
      notes:  string or cell of strings                               
   userdata:  any data type  

set(G,'den',[1 2 1])
G

3、直接获取和修改属性

复制代码 
G.den=[1 1.414 1];
G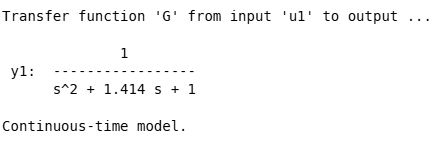

6.3 结构框图的模型表示

1、串联结构

2、并联结构

3、反馈结构

复制代码 
G1=tf(1,[1 2 1])
G2=tf(1,[1 1]);
G3=tf(1,[2 1]);
G4=tf(1,[1 0]);
G12=G1+G2
G34=G3-G4
G=feedback(G12,G34,-1)

Transfer function 'G1' from input 'u1' to output ...

            1      
 y1:  -------------
      s^2 + 2 s + 1

Continuous-time model.

Transfer function 'G12' from input 'u1' to output ...

          s^2 + 3 s + 2    
 y1:  ---------------------
      s^3 + 3 s^2 + 3 s + 1

Continuous-time model.

Transfer function 'G34' from input 'u1' to output ...

       -s - 1  
 y1:  ---------
      2 s^2 + s

Continuous-time model.

Transfer function 'G' from input 'u1' to output ...

           2 s^4 + 7 s^3 + 7 s^2 + 2 s     
 y1:  -------------------------------------
      2 s^5 + 7 s^4 + 8 s^3 + s^2 - 4 s - 2

Continuous-time model.

G1=ss(tf(1,[1 2 1]));
G2=tf(1,[1 1]);
G12=G1+G2

G12.a =
       x1  x2  x3
   x1   0  -1   0
   x2   1  -2   0
   x3   0   0  -1

G12.b =
       u1
   x1  -1
   x2   0
   x3   1

G12.c =
       x1  x2  x3
   y1   0  -1   1

G12.d =
       u1
   y1   0

Continuous-time model.

4、复杂的结构框图

复制代码 
G1=tf(1,[1 0]);
G2=tf(1,[1 1 0]);
G3=tf(1,[1 1 0]);
G4=tf(-2,1);
G5=tf(-1,1);
G6=tf(1,[1 0]);
G7=tf(-1,[1 1]);
Sys=append(G1,G2,G3,G4,G5,G6,G7)

Transfer function 'Sys' from input 'u1' to output ...

      1
 y1:  -
      s

 y2:  0

 y3:  0

 y4:  0

 y5:  0

 y6:  0

 y7:  0

Transfer function 'Sys' from input 'u2' to output ...

 y1:  0

         1   
 y2:  -------
      s^2 + s

 y3:  0

 y4:  0

 y5:  0

 y6:  0

 y7:  0

Transfer function 'Sys' from input 'u3' to output ...

 y1:  0

 y2:  0

         1   
 y3:  -------
      s^2 + s

 y4:  0

 y5:  0

 y6:  0

 y7:  0

Transfer function 'Sys' from input 'u4' to output ...

 y1:  0

 y2:  0

 y3:  0

 y4:  -2

 y5:  0

 y6:  0

 y7:  0

Transfer function 'Sys' from input 'u5' to output ...

 y1:  0

 y2:  0

 y3:  0

 y4:  0

 y5:  -1

 y6:  0

 y7:  0

Transfer function 'Sys' from input 'u6' to output ...

 y1:  0

 y2:  0

 y3:  0

 y4:  0

 y5:  0

      1
 y6:  -
      s

 y7:  0

Transfer function 'Sys' from input 'u7' to output ...

 y1:  0

 y2:  0

 y3:  0

 y4:  0

 y5:  0

 y6:  0

       -1  
 y7:  -----
      s + 1

Continuous-time model.

Q=[1 6 5;
2 1 7;
3 2 0;
4 3 0;
5 4 0;
6 2 0;
7 3 0;];
INPUTS=1;
OUTPUTS=4;
G=connect(Sys,Q,INPUTS,OUTPUTS)

warning: tf: converting to minimal state-space for MIMO TF interconnections

Transfer function 'G' from input 'u1' to output ...

                        -2 s - 2                   
 y1:  ---------------------------------------------
      s^6 + 3 s^5 + 3 s^4 + 1 s^3 - 1 s^2 - 3 s - 3

Continuous-time model.

nblocks=7;
n1=1;d1=[1 0];
n2=1;d2=[1 1 0];
n3=1;d3=[1 1 0];
n4=-2;d4=1;
n5=-1;d5=1;
n6=1;d6=[1 0];
n7=-1;d7=[1 1];
blkbuild
Q=[1 6 5;
2 1 7;
3 2 0;
4 3 0;
5 4 0;
6 2 0;
7 3 0;];
INPUTS=1;
OUTPUTS=4;
[A,B,C,D]=connect(a,b,c,d,Q,INPUTS,OUTPUTS)

error: 'blkbuild' undefined near line 1, column 1

6.4 线性系统的时域分析

6.4.1 零输入响应分析

1、连续系统的零输入响应

复制代码 
G1=tf(12,[1 4]);
H=tf(1,[1 3]);
GG=feedback(G1,H)
G=ss(GG)
initial(G,[1 2])

Transfer function 'GG' from input 'u1' to output ...

        12 s + 36   
 y1:  --------------
      s^2 + 7 s + 24

Continuous-time model.

G.a =
              x1         x2
   x1  8.882e-16        2.4
   x2        -10         -7

G.b =
         u1
   x1  -3.6
   x2    12

G.c =
       x1  x2
   y1   0   1

G.d =
       u1
   y1   0

Continuous-time model.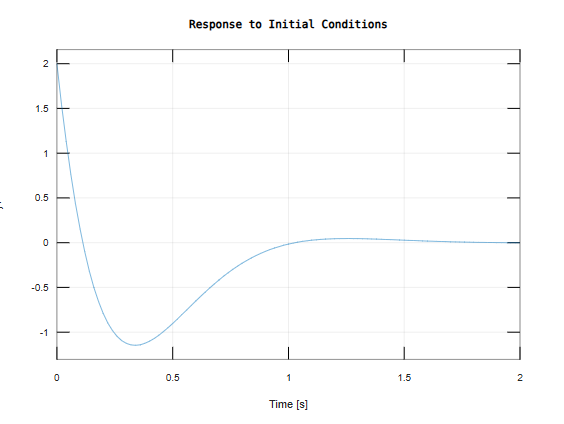

2、离散系统的脉冲响应

6.4.2 脉冲响应分析

1、连续系统的脉冲响应

复制代码 
impulse(G)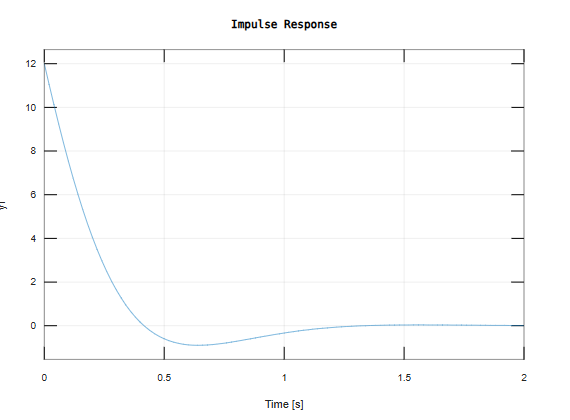
复制代码 
t=0:0.1:10;
y=impulse(G,t)

y =

   1.2000e+01
   7.5497e+00
   4.0623e+00
   1.6432e+00
   1.6386e-01
  -5.9848e-01
  -8.7579e-01
  -8.6531e-01
  -7.1369e-01
  -5.1764e-01
  -3.3270e-01
  -1.8457e-01
  -7.9778e-02
  -1.4242e-02
   2.0712e-02
   3.4565e-02
   3.5596e-02
   3.0085e-02
   2.2258e-02
   1.4605e-02
   8.3333e-03
   3.8090e-03
   9.1778e-04
  -6.7324e-04
  -1.3494e-03
  -1.4569e-03
  -1.2637e-03
  -9.5397e-04
  -6.3875e-04
  -3.7414e-04
  -1.7943e-04
  -5.2379e-05
   1.9574e-05
   5.1993e-05
   5.9295e-05
   5.2887e-05
   4.0757e-05
   2.7837e-05
   1.6711e-05
   8.3587e-06
   2.7966e-06
  -4.3865e-07
  -1.9710e-06
  -2.3984e-06
  -2.2049e-06
  -1.7357e-06
  -1.2090e-06
  -7.4291e-07
  -3.8574e-07
  -1.4311e-07
   1.5897e-09
   7.3178e-08
   9.6345e-08
   9.1548e-08
   7.3676e-08
   5.2335e-08
   3.2882e-08
   1.7658e-08
   7.1104e-09
   6.6947e-10
  -2.6423e-09
  -3.8397e-09
  -3.7847e-09
  -3.1170e-09
  -2.2580e-09
  -1.4494e-09
  -8.0260e-10
  -3.4562e-10
  -6.0204e-11
   9.1714e-11
   1.5164e-10
   1.5574e-10
   1.3142e-10
   9.7109e-11
   6.3639e-11
   3.6251e-11
   1.6517e-11
   3.9221e-12
  -2.9957e-12
  -5.9242e-12
  -6.3760e-12
  -5.5215e-12
  -4.1630e-12
  -2.7839e-12
  -1.6281e-12
  -7.7863e-13
  -2.2505e-13
   8.7922e-14
   2.2846e-13
   2.5960e-13
   2.3114e-13
   1.7789e-13
   1.2135e-13
   7.2742e-14
   3.6295e-14
   1.2055e-14
  -2.0222e-15
  -8.6705e-15
  -1.0505e-14
  -9.6384e-15
  -7.5773e-15

2、离散系统的脉冲响应

复制代码 
a=[-2 0;0 -3];
b=[1;1];
c=[1 -4];
d=1;
dimpulse(a,b,c,d,1,10)

error: 'dimpulse' undefined near line 1, column 1

6.4.3 阶跃响应分析

1、连续阶跃响应

复制代码 
G1=tf(12,[1 4]);
H=tf(1,[1 3]);
G=feedback(G1,H)
step(G)

Transfer function 'G' from input 'u1' to output ...

        12 s + 36   
 y1:  --------------
      s^2 + 7 s + 24

Continuous-time model.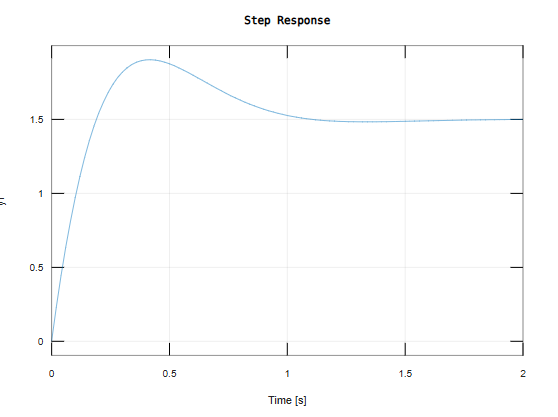
复制代码 
t1=0:0.1:5;
y1=step(G,t1);
plot(t1,y1)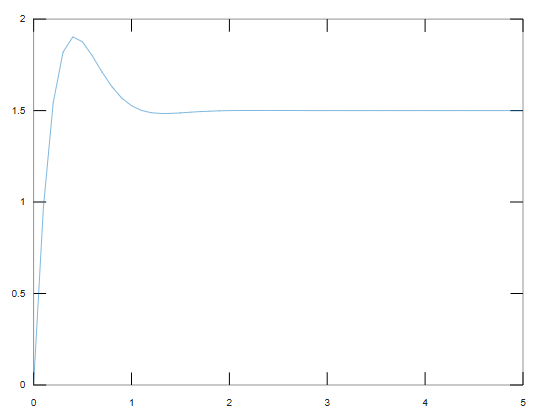
复制代码 
t2=0:0.5:5;
y2=step(G,t2);
plot(t2,y2)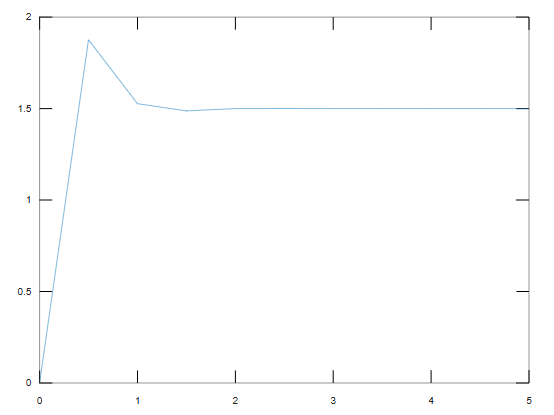

2、离散系统的阶跃响应

6.4.4 任意输入的响应

1、连续系统的任意输入响应

复制代码 
t1=0:0.1:5;
u=sin(t);
G1=tf(1,[1 1.414 1])
G2=tf(1,[1 0.6 1])
lsim(G1,'r',G2,'bo',u,t)

Transfer function 'G1' from input 'u1' to output ...

              1        
 y1:  -----------------
      s^2 + 1.414 s + 1

Continuous-time model.

Transfer function 'G2' from input 'u1' to output ...

             1       
 y1:  ---------------
      s^2 + 0.6 s + 1

Continuous-time model.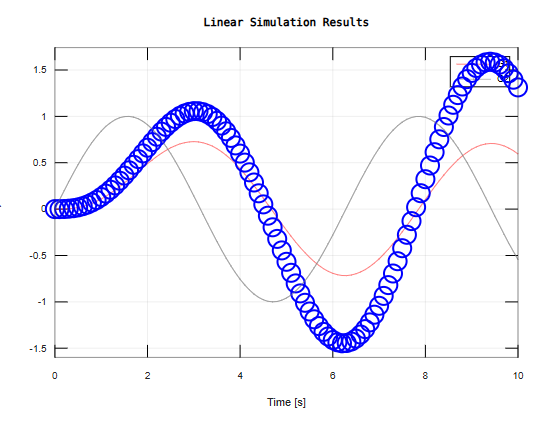

2、离散系统的任意输入响应

复制代码 
num=[2 5 1];
den=[1 2 3];
t=0:0.1:5;
u=sin(t);
y=dlsim(num,den,u)

error: 'dlsim' undefined near line 1, column 3

6.4.5 系统的结构参数

1、极点和零点

复制代码 
num=[5 100];
den=[1 8 32 80 100];
G=tf(num,den);
p=pole(G)
[z,gain]=tzero(G)
[p,z]=pzmap(G)

p =

  -1 + 3i
  -1 - 3i
  -3 + 1i
  -3 - 1i

error: 'tzero' undefined near line 1, column 10

The 'tzero' function belongs to the control package from Octave Forge
but has not yet been implemented.
p =

  -1 + 3i
  -1 - 3i
  -3 + 1i
  -3 - 1i

z = -20

2、闭环系统的阻尼系数和固有频率

复制代码 
[wn,zeta]=damp(G)

wn =

   3.1623
   3.1623
   3.1623
   3.1623

zeta =

   0.9487
   0.9487
   0.3162
   0.3162

3、时域响应的稳态增益

复制代码 
[wn,zeta]=damp(G)

wn =

   3.1623
   3.1623
   3.1623
   3.1623

zeta =

   0.9487
   0.9487
   0.3162
   0.3162
相关推荐
lly2024062 小时前
CSS 颜色名详解
开发语言
Biomamba生信基地2 小时前
用R语言画生信基地圣诞树~
开发语言·r语言·单细胞·空间转录组·biomamba生信基地
Nakkhon2 小时前
软件工程实践——个人技术博客
java·开发语言
embrace992 小时前
【数据结构学习】数据结构和算法
c语言·数据结构·c++·学习·算法·链表·哈希算法
智算菩萨2 小时前
【Python进阶】数据结构的精巧与算法的智慧：AI提速的关键
开发语言·人工智能·python
代码or搬砖2 小时前
== 和 equals() 的区别
java·开发语言·jvm
liwulin05062 小时前
【PYTHON】视频转图片
开发语言·python·音视频
Shirley~~2 小时前
PPTist 画布工具栏
开发语言·前端·javascript
chen_2272 小时前
qt加ffmpeg制作简易录屏工具
开发语言·qt·ffmpeg
热门推荐
01GitHub 镜像站点023D 圣诞树网页代码03从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击04UV安装并设置国内源05Linux下V2Ray安装配置指南06Gemini3 生成的基于手势控制3D粒子圣诞树07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题09开源分享 | 超浪漫 3D 圣诞树立体动画（附零基础使用教程）10GLM-4.7 vs MiniMax-M2.1：代码工程理解