4.1多层感知机
多层感知机在输出层和输入层之间增加一个或多个全连接隐藏层,并通过激活函数转换隐藏层的输出
4.1.1隐藏层
线性模型并不能处理所有的问题,我们可以在网络中加入隐藏层来克服线性模型的限制
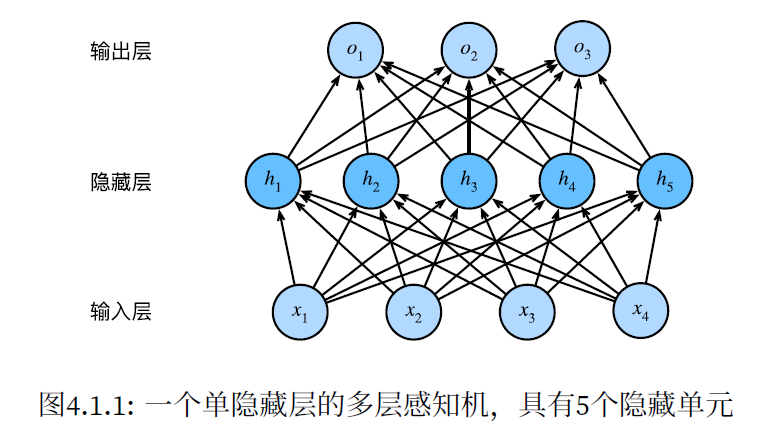
为了发挥多层架构的潜力,我们还需要一个额外的关键要素:在仿射变换之后对每个隐藏单元应用非线性的激活函数
4.1.2激活函数
常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。
ReLU函数------修正线性单元
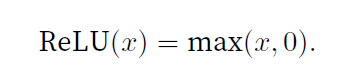
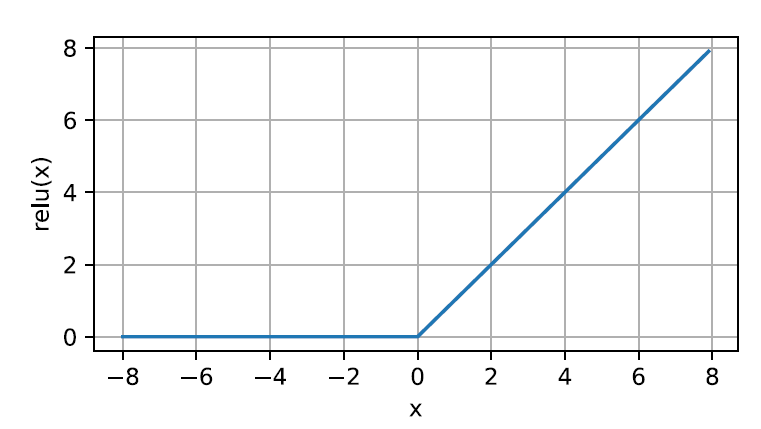
ReLU减轻了困扰以往神经网络的梯度消失问题
sigmoid函数------挤压函数
将输入压缩到区间(0,1)
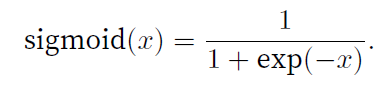
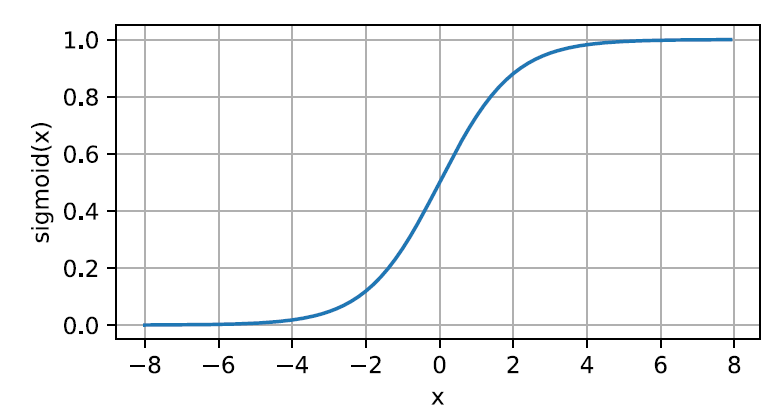
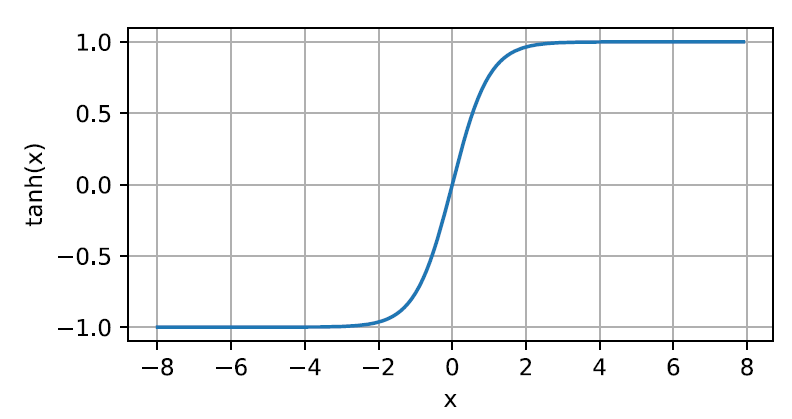
tanh函数------双曲正切
就爱那个输入压缩到区间(-1,1)
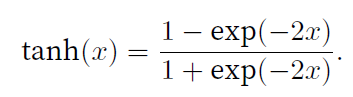
4.2多层感知机的从零开始
从头定义模型和激活函数,损失函数、训练都与简洁实现一样
python
#初始化模型参数
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(torch.randn(
num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))
params = [W1, b1, W2, b2]
#激活函数
def relu(X):
a = torch.zeros_like(X)
return torch.max(X, a)
#模型
def net(X):
X = X.reshape((-1, num_inputs))
H = relu(X@W1 + b1) # 这里"@"代表矩阵乘法
return (H@W2 + b2)手动实现一个简单的多层感知机是很容易的。然而如果有大量的层,从零开始实现多层感知机会变得很麻烦(例如,要命名和记录模型的参数)。
4.3多层感知机的简洁实现
第一层是隐藏层,它包含256个隐藏单元,并使用了ReLU激活函数
python
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
python
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
python
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)对于相同的分类问题,多层感知机的实现与softmax回归的实现相同,只是多层感知机的实现里增加了带有激活函数的隐藏层。
4.4模型选择、欠拟合和过拟合
如何发现可以泛化的模式是机器学习的根本问题
将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合
用于对抗过拟合的技术称为正则化
4.4.1训练误差和泛化误差
训练误差:模型在训练数据集上计算得到的误差
泛化误差:模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望