背包dp——动态规划

文章目录

• 一、0-1背包
• 二、完全背包
• 三、二维费用背包
• 四、似包非包

背包dp，全称是背包类动态规划，是动态规划问题中非常经典的一类问题。它的基本模型来源于一个非常形象的场景------一个容量有限的背包，和一组物品。每个物品都有自己的重量（或体积）和价值。目标是选择一些物品装入背包，使得在不超过背包总容量的前提下，装入背包的物品的总价值最大。

这个看似简单的模型，却可以衍生出许多变种，广泛应用于资源分配、投资决策、项目选择等现实问题中。

根据物品的特点，背包问题还可以进一步细分。如果每种物品只有一个，可以选择将之放入或不放入背包，那么可以将这类问题称为0-1背包问题。0-1背包问题是最基本的背包问题，其他背包问题通常可以转化为0-1背包问题。
  如果第 i i i种物品最多有 M i M_i Mi个（ M i ≥ 1 M_i\geq1 Mi≥1），即每种物品的数量有限，这类背包问题称为有界背包 问题（也常称为多重背包 问题）。如果每种物品的数量都是无限的，那么这类背包问题称为无界背包 问题（也可以称为完全背包问题）。
  二维费用背包问题是传统背包问题的扩展，其核心在于背包的限制条件从一个维度增加到两个维度（例如同时考虑总重量和总体积），除此之外还有混合背包，分组背包等，在此章我们只会讲解0-1背包、完全背包和二维费用背包。

下面通过几个典型的题目来分析如何使用动态规划解决背包问题。

一、0-1背包

0-1背包（模板题）

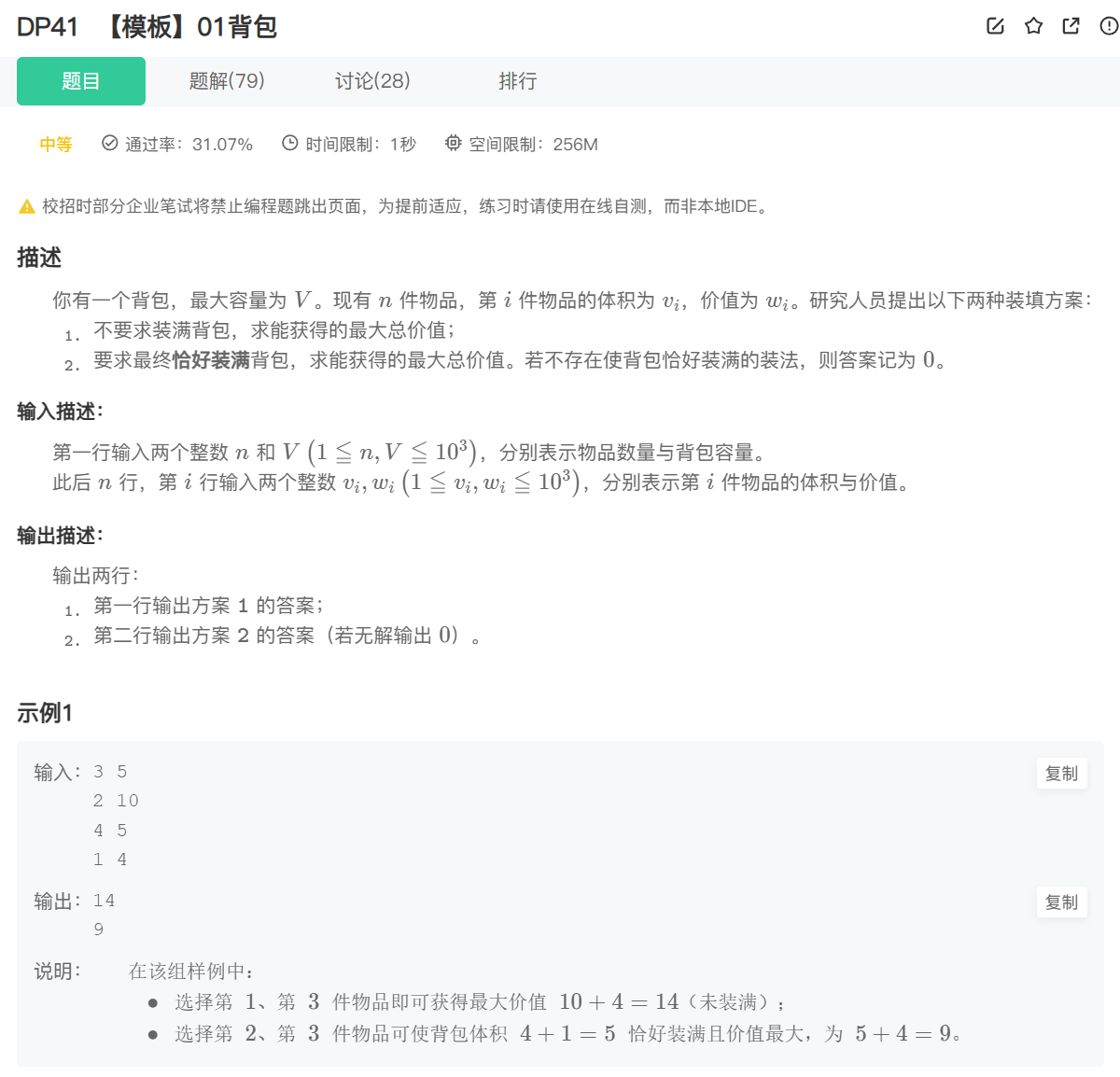
题目解析

有一个背包，最多能容纳的体积是 V V V，有 n n n个物品，体积为 v i v_i vi，价值 w i w_i wi

• 问1：最多能装的最大价值的物品？（背包不必装满）
• 问2：背包恰好装满，最多能装多大价值的物品

如上示例：一个体积为5的背包，提供选择的有三个的物品。

选择物品 1、2、3 或 1、2 均无法全部装入，退一步选择物品 1 和 3 为最优，总价值 14；此时背包虽未装满，但已无合适物品可补充。

而第二问要求背包恰好装满，因此上述组合均不满足条件，仅选择物品 2 和 3（总体积 5）符合要求。

而背包装满的情况也可能不存在，如下：

算法原理
第一问

1. 状态表示

该题本质线性 d p dp dp，因为可以从左往右走，每一个元素有选和不选两种情况，在它们当中选最优。所以状态表示可以是：

• d p [ i ] dp[i] dp[i]表示：从前i个物品中选，所有选法中能挑选出来的最大价值。

值得注意的是背包容量是有限的，在做状态转移方程时，我们无法知道当前选法占背包容量多少，是否还能再选。无法推出状态转移方程。所以需要在加一个维度用来记录占用背包容量情况，即：

• d p [ i ] [ j ] dp[i][j] dp[i][j]：从前 i i i个物品中挑选，总体积不超过 j j j，所有选法中能挑选出来的最大价值。

2. 状态转移方程

分两种情况：

• 不选i物品：等价于从 0 0 0到 i − 1 i-1 i−1中挑的最优价值，所以结果就是 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]
• 选i商品：等价于从 0 0 0到 i − 0 i-0 i−0中挑的最优价值加上当前i物品的价值。但要注意此时容量要增加 v ( i ) v(i) v(i)，根据状态表示，我们需要从 d p [ i − 1 ] [ j − v [ i ] ] dp[i-1][j-v[i]] dp[i−1][j−v[i]]选法的基础上添加 i i i物品才是 d p [ i ] [ j ] dp[i][j] dp[i][j]的最终结果。注意 j − v [ i ] j-v[i] j−v[i]要大于等于 0 0 0。

最后在两种情况中最大价值。

状态转移方程：

d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] , 其他 m a x ( d p [ i − 1 ] [ j ] , w [ i ] + d p [ i − 1 ] [ j − v [ i ] ] ) , ( j − v [ i ] ) ≥ 0 dp[i][j]=\begin{cases} dp[i-1][j] & \text{},其他 \\ max(dp[i-1][j],w[i]+dp[i-1][j-v[i]]) & \text{},(j-v[i])\geq0 \end{cases} dp[i][j]={dp[i−1][j]max(dp[i−1][j],w[i]+dp[i−1][j−v[i]]),其他,(j−v[i])≥0

3. 初始化

为了避免繁琐的边界判断，我们在 d p dp dp表上加一行一列。然后对其初始化：

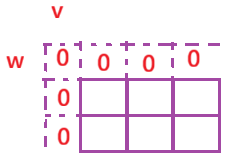
• 因为容量不超过0时，怎么选都是最优价值为0。物品为0时容量多大最优价值都是0。
• 添加行和列后注意数据映射关系。（整体下标减1）

4. 填表顺序

从状态转移方程来看，填写dp[i][j]时需要知道，左边，左上方的数据，所以需要从上往下，从左往右填写。

5. 返回值
   返回选完所有物品，体积不超过背包体积的情况，即 d p [ n ] [ v ] dp[n][v] dp[n][v]

第二问

1. 状态表示
   根据题目要求，我们需要把状态表示改为总体积正好等于j的状态，即：

• dp[i][j]：从前 i i i个物品中挑选，总体积等于 j j j，所有选法中能挑选出来的最大价值。

2. 状态转移方程

与问题一类似需要注意的是体积刚好等于 j j j的情况可能不存在。所以有些 d p dp dp位置无法完成填写。我们把它填入特殊元素-1。

• 不选i物品：等价于从0到i-1中挑的最优价值，所以结果就是 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]，尽管是总体积等于 j j j的情况不存在，在 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]中会做处理。
• 选i商品：在问题一 j − v [ i ] ≥ 0 j-v[i]\geq0 j−v[i]≥0的条件下还要满足 d p [ i − 1 ] [ j − v [ i ] ] dp[i-1][j-v[i]] dp[i−1][j−v[i]]的情况存在。即： ( j − v [ i ] ) ≥ 0 & & d p [ i − 1 ] [ j − v [ i ] ] ! = − 1 (j-v[i])\geq0\&\&dp[i-1][j-v[i]]!=-1 (j−v[i])≥0&&dp[i−1][j−v[i]]!=−1

所以状态表示：

d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] , 其他 m a x ( d p [ i − 1 ] [ j ] , w [ i ] + d p [ i − 1 ] [ j − v [ i ] ] ) , ( j − v [ i ] ) ≥ 0 & & d p [ i − 1 ] [ j − v [ i ] ] ! = − 1 dp[i][j]=\begin{cases} dp[i-1][j] & \text{},其他 \\ max(dp[i-1][j],w[i]+dp[i-1][j-v[i]]) & \text{},(j-v[i])\geq0\&\&dp[i-1][j-v[i]]!=-1 \end{cases} dp[i][j]={dp[i−1][j]max(dp[i−1][j],w[i]+dp[i−1][j−v[i]]),其他,(j−v[i])≥0&&dp[i−1][j−v[i]]!=−1

3. 初始化
   

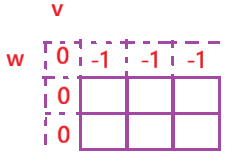
   当总容量为0时，怎么选最优价值都是0，当可选物品为 0 但总容量不为 0 时，无法凑出该容量，因此初始化为 - 1。

4. 填表顺序

   从上往下，从左往右

5. 返回值

   如果 d p [ n ] [ v ] dp[n][v] dp[n][v]为-1则返回0，如果不是则返回 d p [ n ] [ v ] dp[n][v] dp[n][v]

代码编写

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    int n,v;
    cin>>n>>v;
    vector<int> vl(n+1);
    auto wl=vl;
    vector<vector<int>> dp1(n+1,vector<int>(v+1));
    auto dp2=dp1;
    //获取数据
    for(int i=1;i<=n;i++)
    {
        int tv,tw;
        cin>>tv>>tw;
        vl[i]=tv,wl[i]=tw;
    }
    //初始化
    for(int i=1;i<=v;i++) dp2[0][i]=-1;
    //dp表填写
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=v;j++)
        {
            //第一问
            if(j-vl[i]>=0) 
                dp1[i][j]=max(dp1[i-1][j],wl[i]+dp1[i-1][j-vl[i]]);
            else
            		dp1[i][j]=dp1[i-1][j];
            //第二问
            if(j-vl[i]>=0&&dp2[i-1][j-vl[i]]!=-1) 
                dp2[i][j]=max(dp2[i-1][j],wl[i]+dp2[i-1][j-vl[i]]);
            else
            		 dp2[i][j]=dp2[i-1][j];
        }
    }
    cout<<dp1[n][v]<<endl;
    if(dp2[n][v]==-1)cout<<0;
    else cout<<dp2[n][v];
    return 0;
}

优化

初步优化（滚动数组 ）：填写 d p [ i ] [ j ] dp[i][j] dp[i][j]只需要左边，上边，左上角的值，往上两行后的值就没有利用价值了，而往下几行的空间也暂时用不到。所以只需要用两行就能完成 d p dp dp表的填写，需要两行循环往复的利用。

进一步优化：我们尝试把优化成一行，可以发现，当 d p dp dp表填写完 d p [ i ] [ j ] dp[i][j] dp[i][j]后，只有 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]这个位置及往右的元素是有用的，而 d p [ i ] [ j ] dp[i][j] dp[i][j]往右的空间暂时是空闲的，所以可以把原本需要填到上面的元素填在该行后面不用的空间就可以省下一行的空间。

更方便理解的做法是我们使用一个数组，从后往前填写，因为我们用到的是前面的数据，这样做就不会使新数据覆盖前面的有效数据。

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    int n,v;
    cin>>n>>v;
    vector<int> vl(n+1),dp1(v+1);
    auto wl=vl,dp2=dp1;
    for(int i=1;i<=n;i++)
    {
        int tv,tw;
        cin>>tv>>tw;
        vl[i]=tv,wl[i]=tw;
    }
    for(int i=1;i<=v;i++) dp2[i]=-1;
    for(int i=1;i<=n;i++)
    {
        for(int j=v;j>=vl[i];j--)
        {  
            dp1[j]=max(dp1[j],wl[i]+dp1[j-vl[i]]);
            if(dp2[j-vl[i]]!=-1) dp2[j]=max(dp2[j],wl[i]+dp2[j-vl[i]]);
        }
    }
    cout<<dp1[v]<<endl;
    if(dp2[v]==-1)cout<<0;
    else cout<<dp2[v];
    return 0;
}

注意：

• 这是一个模板题，该题的分析思路可以，运用到很多题里面。
• 需强行纠结优化后一维数组的状态表示字面含义，核心是理解'从后往前遍历'避免覆盖有效数据的逻辑，其本质是二维 DP 的空间压缩。

分割等和子集

题目解析

• 该题要求将数组分割为两个子集，使得两个子集的元素和相等。
• 只要存在任意一种分割方式满足条件，返回 true；否则返回 false。

算法原理

由题意可知确定一个数组后是可以知道它分成子集后的和的。它就等于这个数组总和的一半，如果数组总和除以2还有余数呢？这说明该数组无法分成和相同的两个子集。

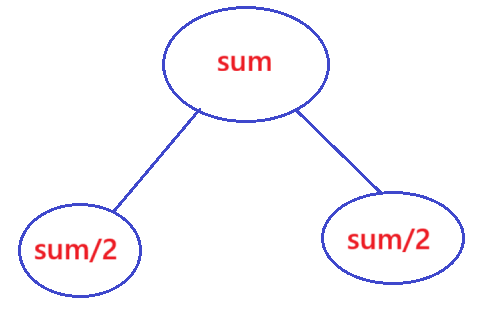
所以我们可以把问题转化为能否抽出数组的一部分元素使得它们的和为 s u m / 2 sum/2 sum/2。这样就成了一个0-1背包问题。

照搬上题分析思路

1. 状态表示

• d p [ i ] [ j ] dp[i][j] dp[i][j]：表示从前 i i i个数中选，所有选法中能否凑成 j j j这个数。是一个bool类型

2. 状态转移方程

在面对一个元素时我们都有选和不选两种情况，只要任意一种情况为true，则为true

• 不选：等价于考虑 0 0 0到 i − 1 i-1 i−1中是否能选出元素和为j的子集。
• 选：等价与在 0 0 0到 i − 1 i-1 i−1是否能选出元素和为 j − n u m s [ i ] j-nums[i] j−nums[i]的子集。要满足 j − n u m s [ i ] ≥ 0 j-nums[i]\geq0 j−nums[i]≥0

所以状态转移方程为：

d p [ i ] [ j ] = { d p [ i − 1 ] [ j ] , 其他 d p [ i − 1 ] [ j ] ∣ ∣ d p [ i − 1 ] [ j − n u m s [ i ] ] , ( j − n u m s [ i ] ) ≥ 0 dp[i][j]=\begin{cases} dp[i-1][j] & \text{},其他 \\ dp[i-1][j]||dp[i-1][j-nums[i]] & \text{},(j-nums[i])\geq0 \end{cases} dp[i][j]={dp[i−1][j]dp[i−1][j]∣∣dp[i−1][j−nums[i]],其他,(j−nums[i])≥0

3. 初始化

   同样的为了不做繁琐的边界判断，我们添加一行一列。
   

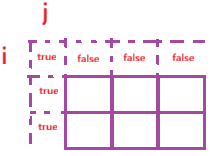
   凑成0的情况为true，在元素个数为0时凑成非零数时为false

4. 填表顺序

   从上往下，左右无所谓

5. 返回值

   返回 d p [ n ] [ s u m / 2 ] dp[n][sum/2] dp[n][sum/2]
   代码编写

class Solution {
public:
    bool canPartition(vector<int>& nums)
    {
        int n=nums.size(),sum=0;
        for(int i=0;i<n;i++) sum+=nums[i];
        if(sum%2) return false;
        vector<vector<bool>> dp(n+1,vector<bool>(sum/2+1));
        for(int i=0;i<=n;i++) dp[i][0]=true;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=sum/2;j++)
            {
                if(j-nums[i-1]>=0) 
                		dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i-1]];
                else
                		dp[i][j]=dp[i-1][j];
            }
        }
        return dp[n][sum/2];    
    }
};

优化

class Solution {
public:
    bool canPartition(vector<int>& nums)
    {
        int n=nums.size(),sum=0;
        for(int i=0;i<n;i++) sum+=nums[i];
        if(sum%2) return false;
        vector<bool> dp(sum/2+1);
        dp[0]=true;
        for(int i=1;i<=n;++i)
            for(int j=sum/2;j>=nums[i-1];--j)
                dp[j]=dp[j]||dp[j-nums[i-1]];
        return dp[sum/2];    
    }
};

二、完全背包

完全背包（模板题）

• 0-1背包：每件物品要么选要么不选（0或1）。
• 完全背包：每件物品可以选0次、1次、2次...直到背包装不下为止。
  与 0-1 背包类似，完全背包也分为两类：背包必须装满、背包不必装满。

题目解析

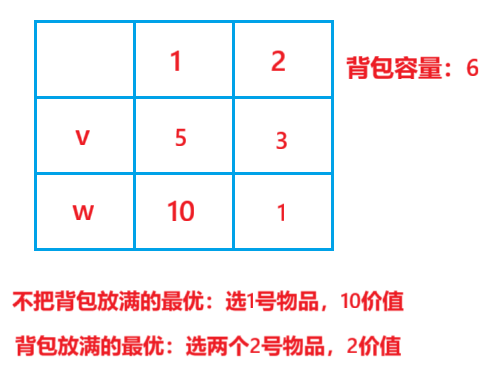
算法原理

第一问

1. 状态表示

与0-1背包相同：

• d p [ i ] [ j ] dp[i][j] dp[i][j]：从前 i i i个物品中选，总体积不超过 j j j，所有选法中最大的价值。

2. 状态转移方程

{ 不选， d p [ i − 1 ] [ j ] 选 1 个， d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] 选 2 个， d p [ i − 1 ] [ j − 2 v [ i ] ] + 2 w [ i ] 选 3 个， d p [ i − 1 ] [ j − 3 v [ i ] ] + 3 w [ i ] . . . . . . \begin{cases} 不选，dp[i-1][j] \\ 选1个，dp[i-1][j-v[i]]+w[i] \\ 选2个，dp[i-1][j-2v[i]]+2w[i] \\ 选3个，dp[i-1][j-3v[i]]+3w[i] \\ ...... \\ \end{cases} ⎩ ⎨ ⎧不选，dp[i−1][j]选1个，dp[i−1][j−v[i]]+w[i]选2个，dp[i−1][j−2v[i]]+2w[i]选3个，dp[i−1][j−3v[i]]+3w[i]......

直到选到 j − k v [ i ] < 0 j−kv[i]<0 j−kv[i]<0（ k k k为选择第 i i i种物品的个数）为止，然后选择价值最大的一种方案。

但这会使我们增加一层循环，时间复杂度为 O ( n 3 ) O(n^3) O(n3)，可以试着用几个状态来表示这些结果优化复杂度。尝试用数学公式推导，如下：

• d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − v [ i ] ] + w [ i ] , d p [ i − 1 ] [ j − 2 v [ i ] ] + 2 w [ i ] . . . . . . d p [ i − 1 ] [ j − k v [ i ] ] + k w [ i ] ) dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]]+w[i], dp[i-1][j-2v[i]]+2w[i]......dp[i-1][j-kv[i]]+kw[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i],dp[i−1][j−2v[i]]+2w[i]......dp[i−1][j−kv[i]]+kw[i])

将上式的j替换为 j − v [ i ] j-v[i] j−v[i]得到：

• d p [ i ] [ j − v [ i ] ] = m a x ( d p [ i − 1 ] [ j − v [ i ] ] , d p [ i − 1 ] [ j − 2 v [ i ] ] + w [ i ] , d p [ i − 1 ] [ j − 3 v [ i ] ] + 2 w [ i ] . . . . . . d p [ i − 1 ] [ j − x v [ i ] ] + ( x − 1 ) w [ i ] ) dp[i][j-v[i]] = max(dp[i-1][j-v[i]], dp[i-1][j-2v[i]]+w[i], dp[i-1][j-3v[i]]+2w[i]......dp[i-1][j-xv[i]]+(x-1)w[i]) dp[i][j−v[i]]=max(dp[i−1][j−v[i]],dp[i−1][j−2v[i]]+w[i],dp[i−1][j−3v[i]]+2w[i]......dp[i−1][j−xv[i]]+(x−1)w[i])

结合两式得：

• d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − v [ i ] ] + w [ i ] ) dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+w[i]) dp[i][j]=max(dp[i−1][j],dp[i][j−v[i]]+w[i])，其中 j − v [ i ] > = 0 j-v[i]>=0 j−v[i]>=0

或许这个推导会唤醒你尘封已久的记忆，即高中数学的错位相减法。

最终的状态表示：

d p [ i ] [ j ] = { m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − v [ i ] ] + w [ i ] ) ， j − v [ i ] ≥ 0 d p [ i − 1 ] [ j ] ，其他 dp[i][j]=\begin{cases} max(dp[i-1][j],dp[i][j-v[i]]+w[i])，j-v[i]\geq0 \\ dp[i-1][j]，其他 \end{cases} dp[i][j]={max(dp[i−1][j],dp[i][j−v[i]]+w[i])，j−v[i]≥0dp[i−1][j]，其他

3. 初始化

   添加一行添加一列，初始化为全0即可

4. 填表顺序

   从上往下，从左往右

5. 返回值

   返回 d p [ n ] [ v ] dp[n][v] dp[n][v]

第二问

1. 状态转移方程

• d p [ i ] [ j ] dp[i][j] dp[i][j]：从前 i i i个物品中选，总体积正好为 j j j，所有选法中最大的价值。

2. 状态转移方程

与0-1背包类似，只需要让无法选出体积正好为j的情况填写为-1，在填 d p dp dp表时添加判断条件。

状态转移方程：
d p [ i ] [ j ] = { m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − v [ i ] ] + w [ i ] ) ， j − v [ i ] ≥ 0 & & d p [ i ] [ j − v [ i ] ] ! = − 1 d p [ i − 1 ] [ j ] ，其他 dp[i][j]=\begin{cases} max(dp[i-1][j],dp[i][j-v[i]]+w[i])，j-v[i]\geq0\&\&dp[i][j-v[i]]!=-1 \\ dp[i-1][j]，其他 \end{cases} dp[i][j]={max(dp[i−1][j],dp[i][j−v[i]]+w[i])，j−v[i]≥0&&dp[i][j−v[i]]!=−1dp[i−1][j]，其他

3. 初始化

初始化时添加一行一列（避免边界判断）：可选物品为 0 时，仅总体积 j = 0 j=0 j=0可行（价值 0），其余非零容量均不可行，因此第一行除 j = 0 j=0 j=0外均初始化为−1。

4. 填表顺序
   从上往下，从左往右
5. 返回值
   d p [ n ] [ v ] dp[n][v] dp[n][v]为 − 1 -1 −1返回 0 0 0，否则返回 d p [ n ] [ v ] dp[n][v] dp[n][v]

代码编写

int main()
{
    int n,m;
    cin>>n>>m;
    vector<int> v(n),w(n);
    for(int i=0;i<n;i++) cin>>v[i]>>w[i];
    vector<vector<int>> dp1(n+1,vector<int>(m+1));
    auto dp2=dp1;
    for(int j=1;j<=m;j++) dp2[0][j]=-1;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            dp1[i][j]=dp1[i-1][j];
            dp2[i][j]=dp2[i-1][j];
            if(j-v[i-1]>=0)
                dp1[i][j]=max(dp1[i][j],dp1[i][j-v[i-1]]+w[i-1]);
            if(j-v[i-1]>=0&&dp2[i][j-v[i-1]]!=-1)
                dp2[i][j]=max(dp2[i][j],dp2[i][j-v[i-1]]+w[i-1]);
        }
    }
    cout<<dp1[n][m]<<endl;
    if(dp2[n][m]==-1) cout<<0;
    else cout<<dp2[n][m];
    return 0;
}

空间优化

与0-1背包不同的是，在填写 d p [ i ] [ j ] dp[i][j] dp[i][j]时所需要的数据就在本行，而且是在它的左边，所以在填写降维后的 d p dp dp表时需要从左往右填写。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
    int n,m;
    cin>>n>>m;
    vector<int> v(n),w(n);
    for(int i=0;i<n;i++) cin>>v[i]>>w[i];
    vector<int> dp1(m+1);
    auto dp2=dp1;
    for(int j=1;j<=m;j++) dp2[j]=-0x3f3f3f3f;
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i-1];j<=m;j++)
        {
            dp1[j]=max(dp1[j],dp1[j-v[i-1]]+w[i-1]);
            dp2[j]=max(dp2[j],dp2[j-v[i-1]]+w[i-1]);
        }
    }
    cout<<dp1[m]<<endl;
    if(dp2[m]<0) cout<<0;
    else cout<<dp2[m];
    return 0;
}

三、二维费用背包

盈利计划

题目解析

给两个数组，用i表示下标，那么profit[i]表示i任务的利润，group[i]则表示完成i任务需要的人数。要求从这些任务中挑选若干个，满足 总利润 ≥ m i n P r o f i t 总利润\geq minProfit 总利润≥minProfit 且 总人数 ≤ n 总人数\le n 总人数≤n，返回有多少种满足条件的方案。

示例1解析：

人数为 n = 5 n=5 n=5个，利润需要超过 3 3 3，任务分别需要的人数 [ 2 , 2 ] [2, 2] [2,2]，任务分别能得到的利润 [ 2 , 3 ] [2, 3] [2,3]

• 挑选0任务：消耗2人<5，利润=2<3，不满足要求
• 挑选1任务：消耗2人<5，利润=3=3，满足要求
• 挑选0,1任务：消耗4人<5，利润=2+3>3，满足要求

所以有两种计划。

算法原理

1. 状态表示

同样的该题也是在数组元素上做选择，只有选和不选两种情况，0-1背包有背包容量限制，而这里有两个限制条件 总利润 ≥ m i n P r o f i t 总利润\geq minProfit 总利润≥minProfit ， 总人数 ≤ n 总人数\le n 总人数≤n，因为有两个限制条件，所以是二维费用的0-1背包问题。

参考0-1背包的分析思路，该题只需要在此基础上多加一个维度。即：

• d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k]：从前 i i i个任务中挑选，总人数不超过 j j j，总利润至少为 k k k，一共有多少种选法

2. 状态转移方程

对于一个 i i i任务有两种情况：

• 不选：等价于从前 i − 1 i-1 i−1个任务中挑选，总人数不超过 j j j，总利润至少为 k k k，选法个数，即 d p [ i − 1 ] [ j ] [ k ] dp[i-1][j][k] dp[i−1][j][k]
• 选：等价于从前 i − 1 i-1 i−1个任务中挑选，总人数不超过 j − g r o u p [ i ] j-group[i] j−group[i]，总利润至少为 k − p r o f i t [ i ] k-profit[i] k−profit[i]，选法个数，注意这里 j − g r o u p [ i ] j-group[i] j−group[i]不能小于0，如果小于也就是 g r o u p [ i ] > j group[i]>j group[i]>j不满足状态表示中人数不超过 j j j的条件，而如果 k − p r o f i t [ i ] k-profit[i] k−profit[i]小于0是可以的，也就是 p r o f i t [ i ] > k profit[i]>k profit[i]>k，满足状态表示中总利润至少为 k k k的条件。

因为需要统计所有满足要求的选法总数，所以将两种情况相加，即：

d p [ i ] [ j ] [ k ] = { d p [ i − 1 ] [ j ] [ k ] ，其他 d p [ i − 1 ] [ j ] [ k ] + d p [ i − 1 ] [ j − g r o u p [ i ] ] [ k − p r o f i t [ i ] ] ， j − g r o u p [ i ] ≥ 0 dp[i][j][k]=\begin{cases} dp[i-1][j][k]，其他\\ dp[i-1][j][k]+dp[i-1][j-group[i]][k-profit[i]]，j-group[i]\geq0 \end{cases} dp[i][j][k]={dp[i−1][j][k]，其他dp[i−1][j][k]+dp[i−1][j−group[i]][k−profit[i]]，j−group[i]≥0

3. 初始化

添加一行一列防止越界，因为当任务为0时和最少产生利润为0时，无论有多少人都能满足要求，所以 d p [ 0 ] [ j ] [ 0 ] = 1 dp[0][j][0]=1 dp[0][j][0]=1（将所有的j初始化为1）

4. 填表顺序
   因为填写 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k]时需要的是上一个二维 d p dp dp表的信息，所以 i i i从 0 0 0依次往后填写， j j j和 k k k可随意。
5. 返回值
   返回 d p [ g r o u p . s i z e ( ) ] [ n ] [ m i n P r o f i t ] dp[group.size()][n][minProfit] dp[group.size()][n][minProfit]

代码编写

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
    {
        int m=group.size();
        vector<vector<vector<int>>> dp(m+1,vector<vector<int>>(n+1,vector<int>(minProfit+1)));
        for(int i=0;i<=n;i++) dp[0][i][0]=1;
        for(int i=1;i<=m;i++)
        {
            for(int j=0;j<=n;j++)
            {
                for(int k=0;k<=minProfit;k++)
                {
                    if(j-group[i-1]>=0)
                        dp[i][j][k]=dp[i-1][j][k]+dp[i-1][j-group[i-1]][max(0,k-profit[i-1])];
                    else
                        dp[i][j][k]=dp[i-1][j][k];
                    dp[i][j][k]%=1000000007;
                }
            }
        }
        return dp[m][n][minProfit];
    }
};

空间优化

class Solution {
public:
    int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit)
    {
        int m=group.size();
        vector<vector<int>> dp(n+1,vector<int>(minProfit+1));
        for(int i=0;i<=n;i++) dp[i][0]=1;
        for(int i=1;i<=m;i++)
        {
            for(int j=n;j>=group[i-1];j--)
                for(int k=minProfit;k>=0;k--)
                {
                        dp[j][k]+=dp[j-group[i-1]][max(0,k-profit[i-1])];
                        dp[j][k]%=1000000007;
                }
        }
        return dp[n][minProfit];
    }
};

四、似包非包

组合总和IV

题目解析

给一个数组和一个目标值，要求从数组中选出一些元素使得元素之和等于目标值。从如上示例中可以看出一个元素可以选无限个，而且一组元素做不同排列也算满足条件。从数学定义来看，组合不考虑元素顺序，排列则强调顺序。本题要求"不同排列算不同方案"，本质是求排列数，题目名称中的"组合"容易产生误导。

"似包非包"顾名思义就是看上去像背包问题，事实上并不是。该题像完全背包问题，但背包问题通常都是"组合"问题，不考虑元素的顺序性，不能用背包 d p dp dp的解题思路来分析该题。

算法原理

1. 状态表示

我们试着用最原始的动态规划分析思路进行讲解------通过将复杂问题分解为更小的子问题来解决的算法思想，尤其适用于具有重叠子问题和最优子结构的优化问题。其核心目标是避免重复计算，通过存储中间结果（记忆化）来提升效率。

这样去想就好办得多，把它划分成子问题，先得到和为 t a r g e t − 1 、 t a r g e t − 2...... target-1、target-2...... target−1、target−2......的组合数。再想办法从前面的结果信息得到最后的答案。

状态表示：

• dp[i]：凑成总和为i，一共有多少种排列数

注意：若按传统背包"前 i 个元素"的状态套路设计，无法体现"排列顺序"的差异，因此不适用。

2. 状态转移方程

• d p [ i ] = ∑ j = 0 n d p [ i − n u m s [ j ] ] dp[i]=\sum_{j=0}^{n}dp[i-nums[j]] dp[i]=∑j=0ndp[i−nums[j]]

填到每个目标值时去循环把所有选法都遍历一遍（遍历 n u m s nums nums），并把每种情况都累加。

• 注意：虽然每个元素都能选多个，但在 d p [ i − n u m s [ j ] ] dp[i-nums[j]] dp[i−nums[j]]中已经把选则多个 n u m s [ j ] nums[j] nums[j]的情况考虑进去了。

3. 初始化

为使后面的填表正确，需要把0下标初始化为1。也可以强行理解为和为0的排列也就是什么也没有，即什么也不选，所以有一种情况。

4. 填表顺序

   从左往右

5. 返回值

   返回 d p [ t a r g e t ] dp[target] dp[target]

代码编写

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        vector<unsigned int> dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 1; i <= target; ++i)
        {
            for (int val : nums)
            {
                if (val <= i) dp[i] += dp[i - val];
                else break;
            }
        }
        return dp[target];
    }
};

此题的解法有很多，如果本章不是动态规划，更让人容易想到的可能是递归或记忆递归，接下来我依次给出代码：

递归（超时）

class Solution
{
public:
    int count=0;
    int combinationSum4(vector<int>& nums, int target)
    {
        sort(nums.begin(),nums.end());
        int sum=0;
        dfs(nums,target,sum);
        return count;
    }
    void dfs(vector<int>& nums, int target ,int sum)
    {
        if(sum>=target)
        {
            if(sum==target) count++;
            return;
        }
        for(int i=0;i<nums.size();i++)
        {
            dfs(nums,target,sum+nums[i]);
        }
    }
};

记忆递归

class Solution {
public:
    unordered_map<int, int> memo;
    int combinationSum4(std::vector<int>& nums, int target)
    {
        sort(nums.begin(), nums.end());
        return dfs(nums, target);
    }

    int dfs(std::vector<int>& nums, int target)
    {
        if (target == 0) return 1;
        if (memo.find(target)!= memo.end()) return memo[target];
        int count = 0;
        for (int num : nums)
        {
            if (num <= target) count += dfs(nums, target - num);
        }
        memo[target] = count;
        return count;
    }
};

非常感谢您能耐心读完这篇文章。倘若您从中有所收获，还望多多支持呀！